模拟分析壳程结构参数对缠绕管式换热器综合性能的影响

陈晓彦, 黄云云， 张朱武， 黄永曙

(1. 福州大学石油化工学院， 福建 福州 350108; 2. 福建省晋华集成电路有限公司， 福建 泉州 362200)

0 引言

缠绕管式换热器由于具有结构紧凑、 换热系数高和传热温差小等特点， 备受市场青睐， 其流体力学性能和热力学性能的研究也由此得到了国内外学者的广泛关注. Yan等[1]与Zhao等[2]通过实验的方法， 证明缠绕管式换热器的能效受壳程流体的动力学和热力学特性影响明显. 壳程结构参数的变化可带来其间流体的力学性能的改变， 从而改变缠绕管式换热器的性能. 通过传统实验方法寻求不同状态流体的最优换热器结构需要耗费大量资源， 若可建立高精度数值模型寻优则可大大降低成本. 李书磊等[3]采用了VOF多相流和标准k-ε湍流相结合的数值模型， 求解了带有不同管径的缠绕管换热器的换热系数， 与实验结果对比， 两者的差异在±5%以内， 可认为采用数值模拟手段对换热器传热和流动性能进行评价可行. Lu等[4]研究发现， 对于管、 壳程均为富甲醇蒸汽的缠绕管式换热器， RNGk-ε模型精度最高. Wan等[5-6]基于火积理论得到传热耗散和摩擦耗散热阻函数， 将两者设为目标函数， 利用多目标遗传算法得到了层间距、 螺旋角、 轴向间距和管径的最优组合. 高兴辉等[7]分别对Standardk-ε、 RNGk-ε和Realizablek-ε3种湍流模型应用于壳程为饱和水的缠绕管式换热器的精度进行了考察， 认定Realizablek-ε模型的计算结果与实际情况最为接近， 以此为基础对缠绕管直径、 平均缠绕直径和螺距3个参数与流动、 换热性能之间的关系和敏感程度进行了分析. 本研究基于Realizablek-ε湍流模型， 选择还未被深入探讨的盘管层数、 垫条厚度和轴向间距作为待考察结构参数， 除了采用努赛尔数和阻力系数外， 还引入了综合性能评价因子考察换热器的传热、 流动和整体性能， 以期通过相关研究， 为缠绕管式换热器的优化设计提供参考.

1 缠绕管式换热器模型设计

1.1 评价指标的定义

努赛尔数(Nu)表征了对流换热的强烈程度， 其表示如下式所示.

Nu=hDtube/λ

(1)

其中：h为对流换热系数， W·(m2·K)-1；λ为导热系数， W·(m·k)-1；Dtube为换热管外径， m.

阻力系数(f)表征了流体流过换热器壳程时由于阻力损失的能量大小， 其表达式为

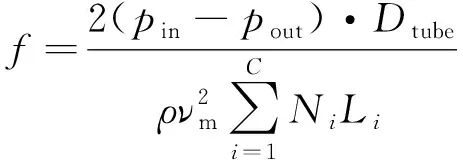
(2)

其中：pin为流体入口静压， Pa；pout为流体出口静压， Pa；ρ为流体密度， kg·m-3；vm为壳程最小流通截面处的流体速度， m·s-1；Ni为第i层缠绕管的排管数；Li为第i层缠绕管的长度， m.

综合性能评价因子(η)综合了努赛尔数对换热性能的评价和阻力系数对流通性能的评价， 表征了换热器的总体能效水平， 其表示为

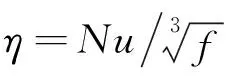
(3)

用雷诺数(Re)来表征不同状态下流体的流动状态， 雷诺数的表达式为

Re=ρνmDtube/μ

(4)

其中:μ为流体的动力粘度， Pa·s.

1.2 数值计算模型的建立

缠绕管式主要由壳体、 换热管束和中心筒组成[8]， 其结构如图1所示. 以换热器壳体轴向中心线向上48.5 mm、 向下48.5 mm截取换热段作为研究对象， 计算域的情况如图2所示. 换热器中段壳侧的物理模型具有对称性， 考虑网格数量对运算速度的影响， 仅取壳侧0°～36°的扇形区域作为模拟对象[9-10].

模拟过程采用Fluent软件. 在湍流区域， 采用Realizablek-ε湍流模型对流动和传热进行模拟， 该模型在进行曲率变化大的流动计算时具有更好的适应性和收敛性[11]. 在低Re区域和非充分发展的湍流固体壁面附近则采用可缩放壁面函数， 不影响细化网格的计算精度的同时避免计算结果劣化. 对模型壳程流体的流动与传热过程进行以下几点简化： 设定换热管壁为恒温壁； 忽略垫条体积对传热和流动过程的影响； 忽略由于密度变化造成的自然对流现象； 不考虑流体重力的影响； 对壳程进出口段进行了适当的延长， 忽略进出口尺寸对流动和换热带来的影响. 设置缠绕管式换热器的中心筒外壁面和壳体内壁为绝热及无滑移壁面， 换热管外壁为恒温且无滑移壁面. 取缠绕管式换热器壳程的轴向截面为边界对称截面. 壳程进口设置为速度进口条件， 出口处设置压力出口条件.

流过换热器壳层的流体为饱和水， 进口温度69 ℃. 壳程进出口流体的温度变化通常不大， 可将壳程流体的物性参数设置为统一数值. 模型的边界条件设置如表1所示. 模型的主要结构参数如表2所示.

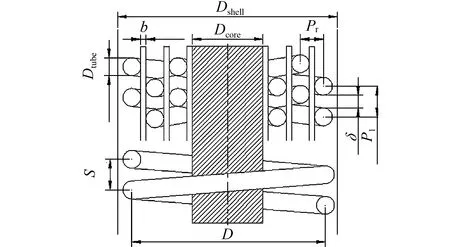
图1 缠绕管式换热器轴向剖面图Fig.1 Axial profile of wound-tube heat exchanger

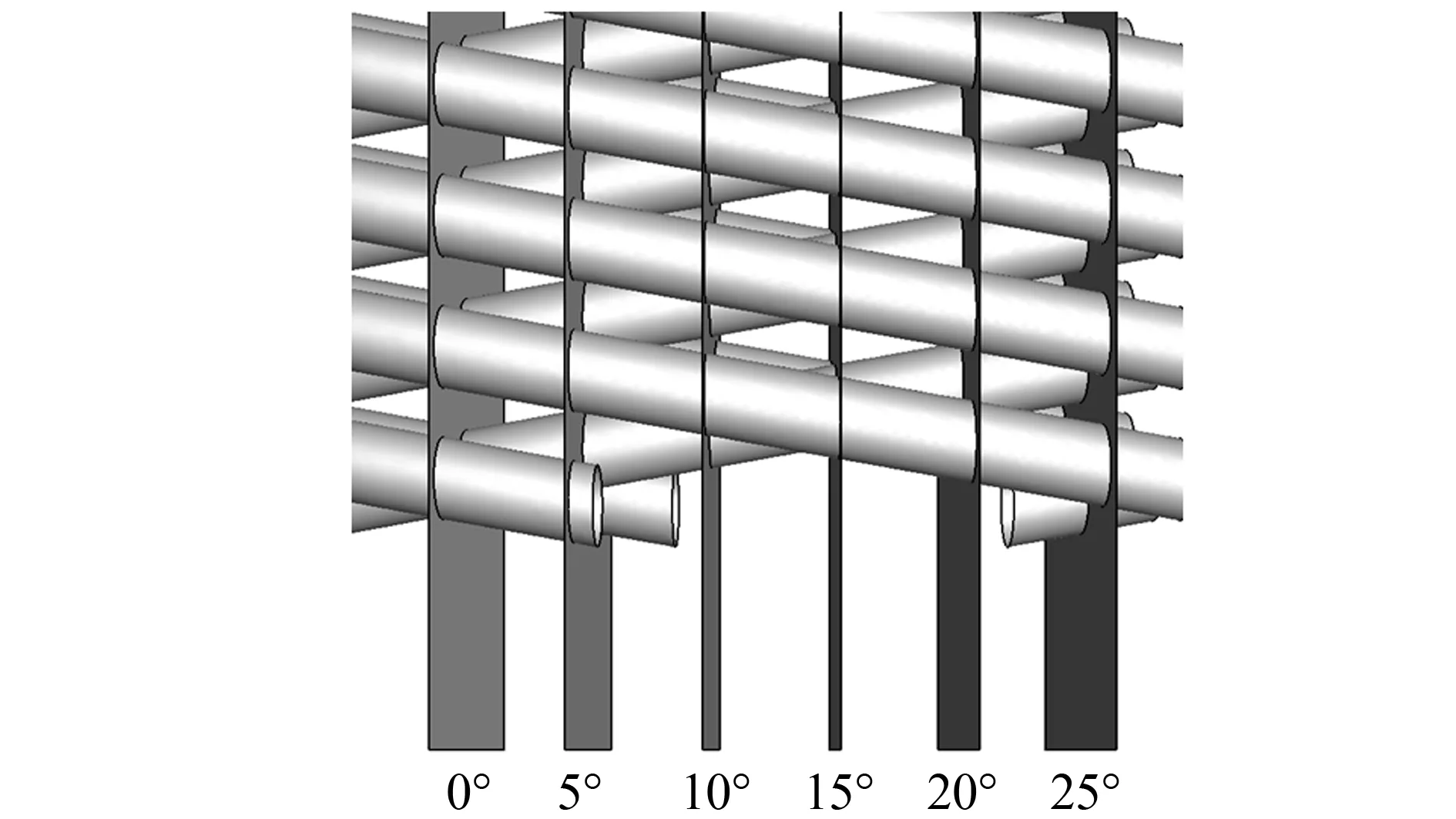
图2 缠绕管式换热器计算流域结构图Fig.2 Simulated basin structure of wound-tube heat exchanger

表1 边界条件设置

表2 模型结构参数

1.3 数值计算方法精度检验

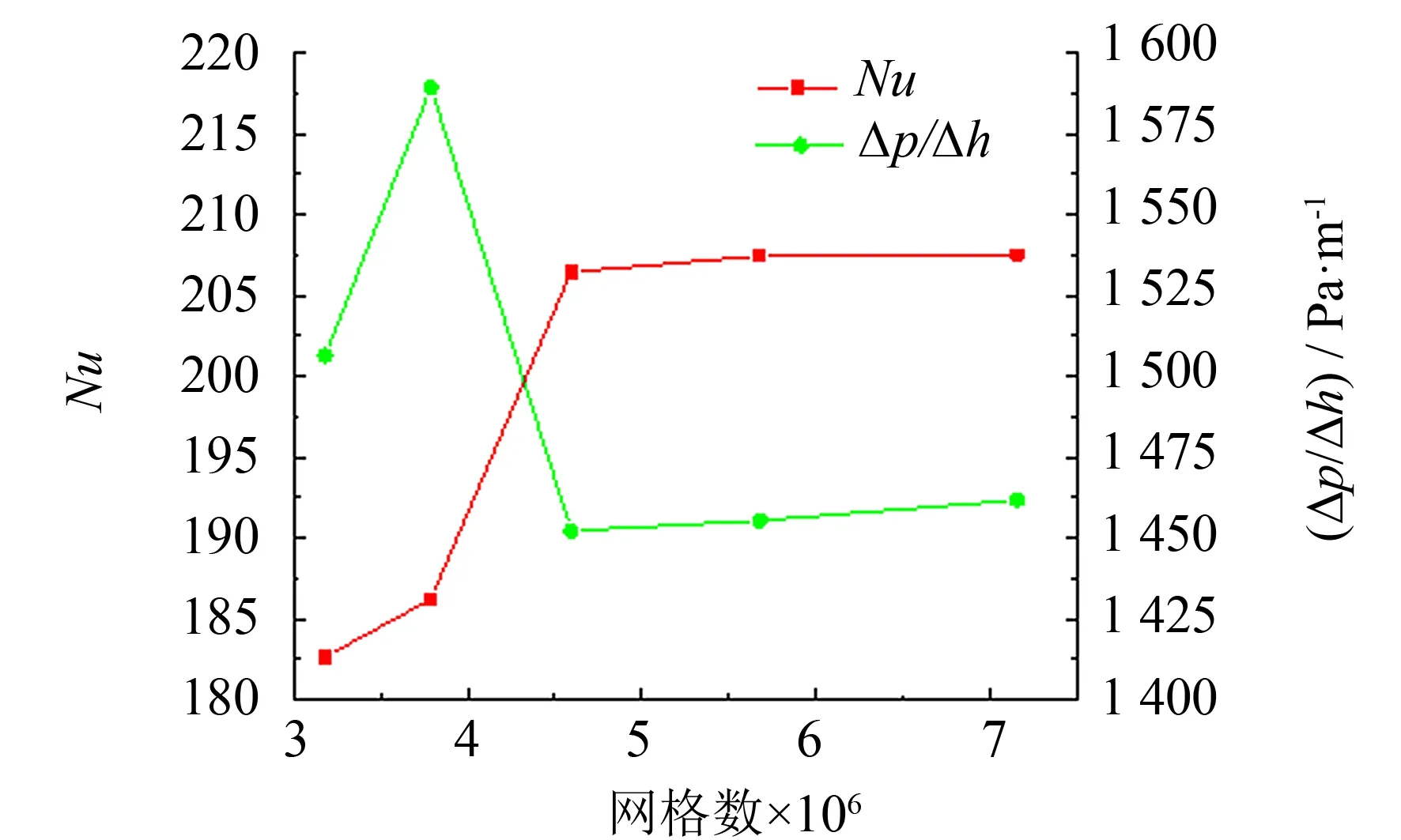
图3 网格无关性验证Fig.3 Irrelevance verification of the grid

验证网格划分方案对模型精度的影响， 模拟结果如图3所示. 网格数为4 595 067时换热器的单位高度压降与网格数为7 157 449时的偏差为-0.39%， 两者Nu数之间偏差也仅为-1.18%， 可以认为当网格增至4 595 067， 模拟的结果将不再受网格数量的影响， 本研究采用网格数为4 595 067的方案. 将数值模型的模拟结果与文献[12]中的实验结果列于图4、 5. 从图中可以看出， 模拟值能较好拟合实验值， 实验值和模拟值随Re数的增加， 呈现出相同趋势.Nu数的模拟值与文献中实验值的误差为11.43%，Δp/Δh的误差为9.46%， 可认为采用的数值模拟方法可靠.

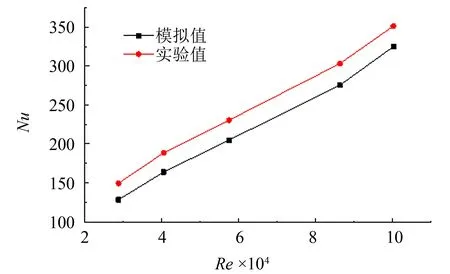
图4 Nu数的模拟值与实验值比较Fig.4 Comparison of simulated value and rxperimental value of Nussel number

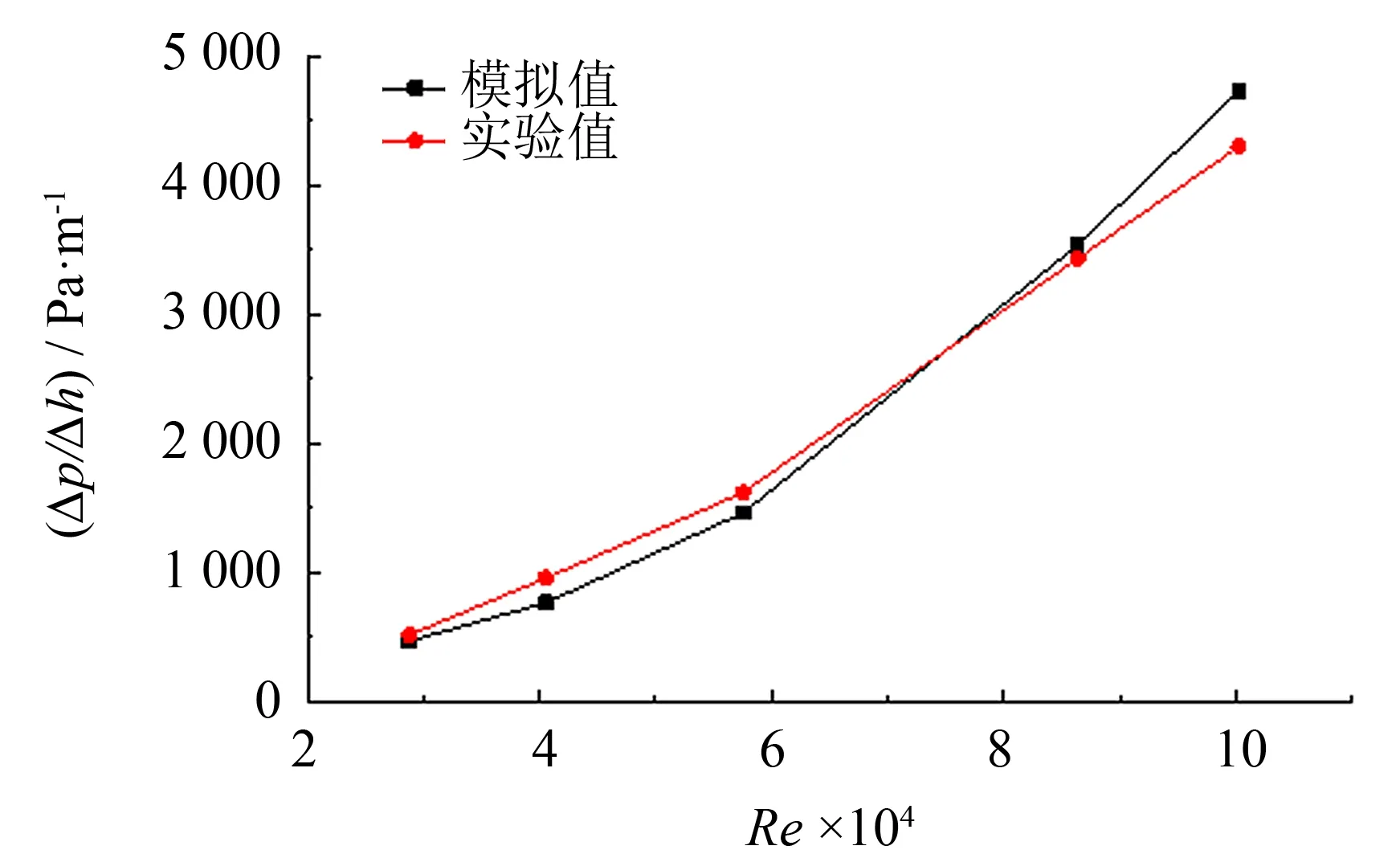
图5 单位高度压降模拟值与实验值比较Fig.5 Comparison of simulated and experimental value of unit height pressure drop

2 数值模拟结果分析

2.1 盘管层数对换热和流动的影响

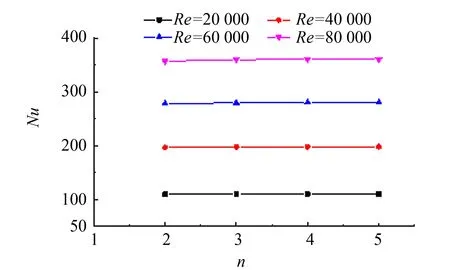
图6 Nu数与盘管层数的关系 Fig.6 Relationship between Nussel number and the layer number of coil

模拟计算了4组不同盘管层数的模型的3项评价指标. 4个模型在不同工况下的指标如图6～8所示.

图6可以看出， 带有不同盘管层数的换热器在相同Re数工况下的Nu数几乎相等， 最大偏差出现在盘管层数为2时， 但与其它模型之间相对偏差小于1%， 可认为盘管层数不对Nu数造成影响. 由图7可以看出， 盘管层数的增加带来内外壁面附近的短流影响减小， 造成阻力系数随盘管层数的增加而增大. 由图8可知， 虽然阻力系数随盘管层数的变化有较大波动， 但由于综合性能评价因子对其变化敏感程度低， 受Nu数几乎不变的影响， 其值也并未随着随盘管层数的变化表现出明显波动.

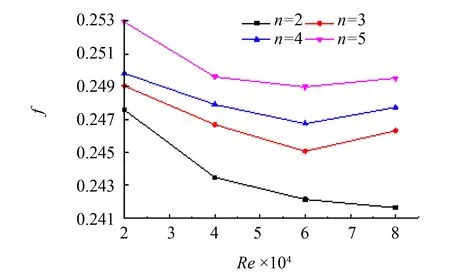
图7 阻力系数与盘管层数的关系Fig.7 Relationship between drag coefficient and the layer number of coil

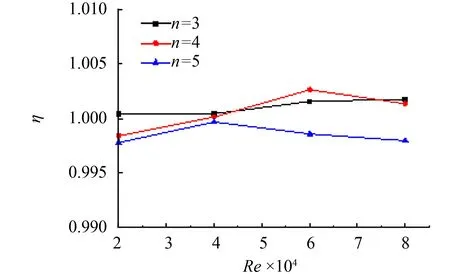
图8 综合性能评价因子与盘管层数的关系Fig.8 Relationship between comprehensive performance evaluation factor and the layer number of coil

2.2 换热管轴向间距对换热和流动的影响

建立不同轴向间距的缠绕管式换热器模型， 6组模型在不同工况下的3项评价指标如图9～11所示. 由图9可以看出， 在Re数相同的情况下，Nu数略微呈现随轴向间距的增大先增加后减小的趋势. 最大偏差出现在轴向间距4 mm时， 但最大相对偏差均小于2%， 可认为Nu数受轴向间距的影响不大. 由图10、 11可以看出， 阻力系数和综合性能评价因子均随轴向间距的增加呈现先增加后减小趋势， 两者的区别在于阻力系数折线的拐点出现在轴向间距为6 mm时， 综合性能评价因子折线的拐点出现在轴线间距为8 mm时.

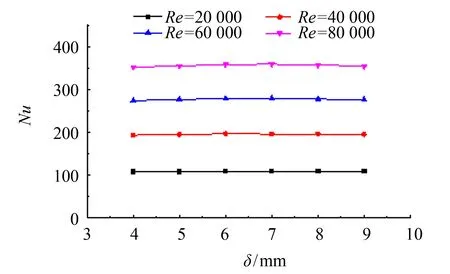
图9 Nu数与轴向间距的关系Fig.9 Relationship between Nussel number and the axial spacing of heat exchangers

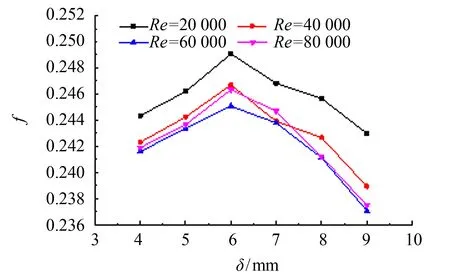
图10 阻力系数与轴向间距的关系Fig.10 Relationship between drag coefficient and the axial spacing of heat exchangers

从壳侧流体流动状态入手分析上述结果的成因， 见图12. 从图12可以看出，Re数同为20 000， 当轴向间距从4 mm增加至9 mm， 壳程流体的径向平均流动速度从0.051 4 m·s-1逐渐上升至0.052 8 m·s-1后又降低至0.051 9 m·s-1； 湍流动能也随之从0.005 97 J增加至0.006 31 J后又减小至0.006 23 J. 在流体绕流多个柱体的过程中， 在上游圆柱收到阻挡会导致其在流过下游圆柱时所受阻力大幅减小[13]. 流体流动的阻力系数在间距刚开始增大的情况下， 由于上述效应， 先快速增大； 随着间距的进一步增大， 上述效应的效果减弱， 阻力系数趋于稳定. 随着轴向间距的增大， 暖色所代表的较大径向速度的区域随之开始扩张， 当轴向间距增加到8 mm后扩张趋于稳定. 径向速度提高将带来更好的换热效果，Nu数随径向速度的变化呈现相同趋势.

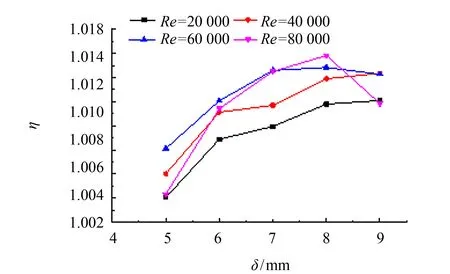
图11 综合性能评价因子与轴向间距的关系Fig.11 Relationship between comprehensive performance evaluation factor and the axial spacing of heat exchangers

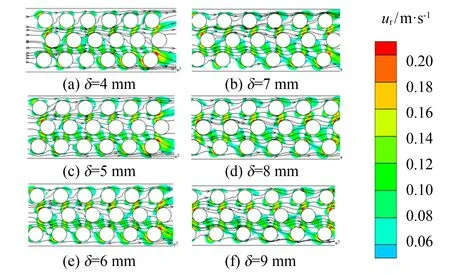
图12 不同轴向间距的换热器模型的径向速度云图与流线图Fig.12 Radial velocity cloud and flow diagram of a model with different axial spacing of heat exchangers

2.3 垫条厚度对换热和流动的影响

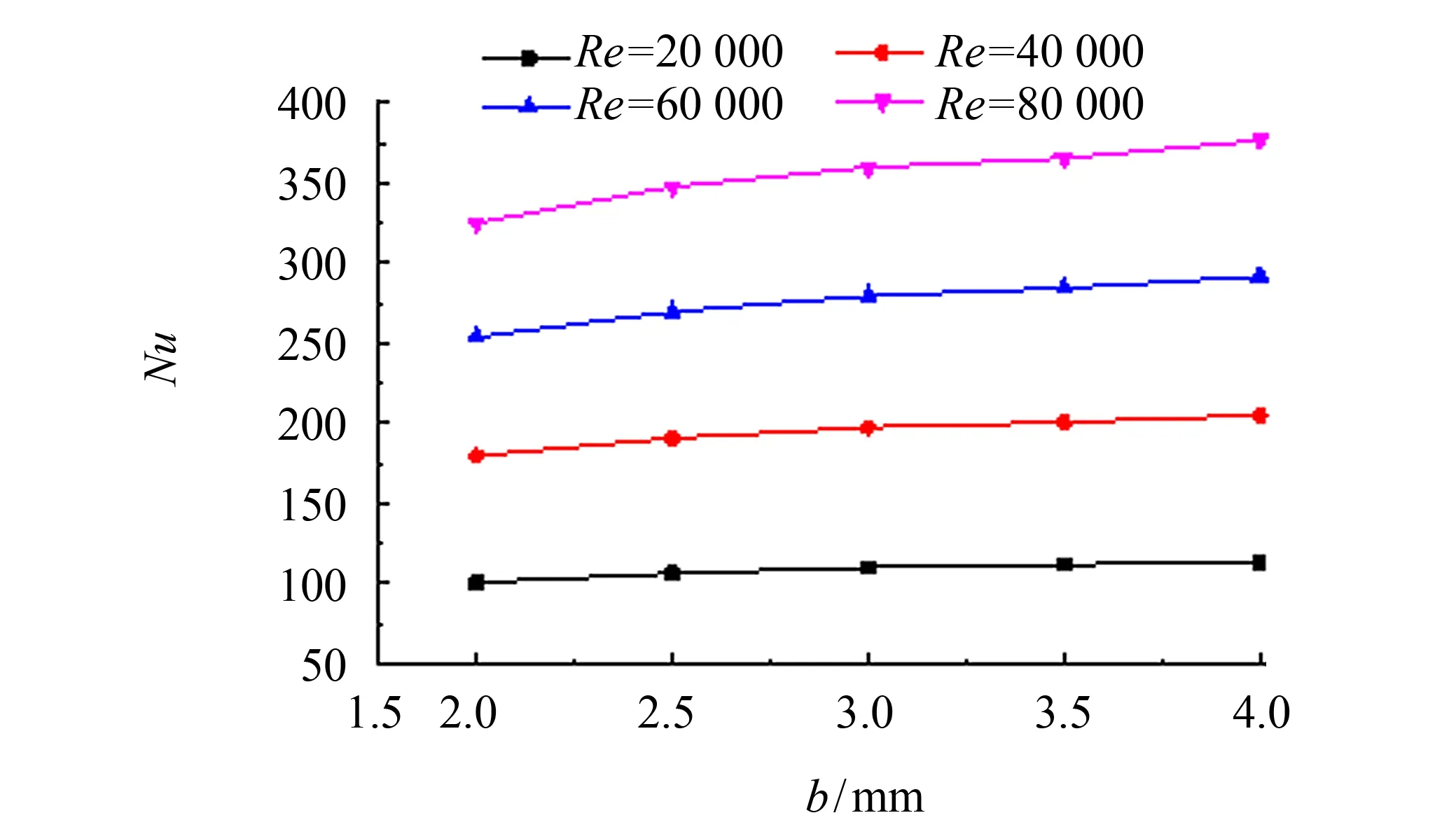
图13 Nu数与垫条厚度的关系 Fig.13 Relationship between Nussel number and the cushion thickness

建立不同垫条厚度的换热器模型， 计算5个模型在不同工况下的各项性能指标， 情况如图13～15所示. 由图13可以看出， 相同Re数情况下，Nu数随着垫条厚度的增加而增大， 即垫条厚度越大， 流体对流换热的效果越好. 由图14可见， 阻力系数随着垫条厚度的增加呈现减少趋势. 由此可得， 综合性能评价因子随着垫条厚度b的增加将会有所增大， 结果如图15所示， 并且随着Re数的增加， 综合性能评价因子增大的速度越快， 说明Re数越大， 垫条厚度对综合性能评价因子的影响越显著.

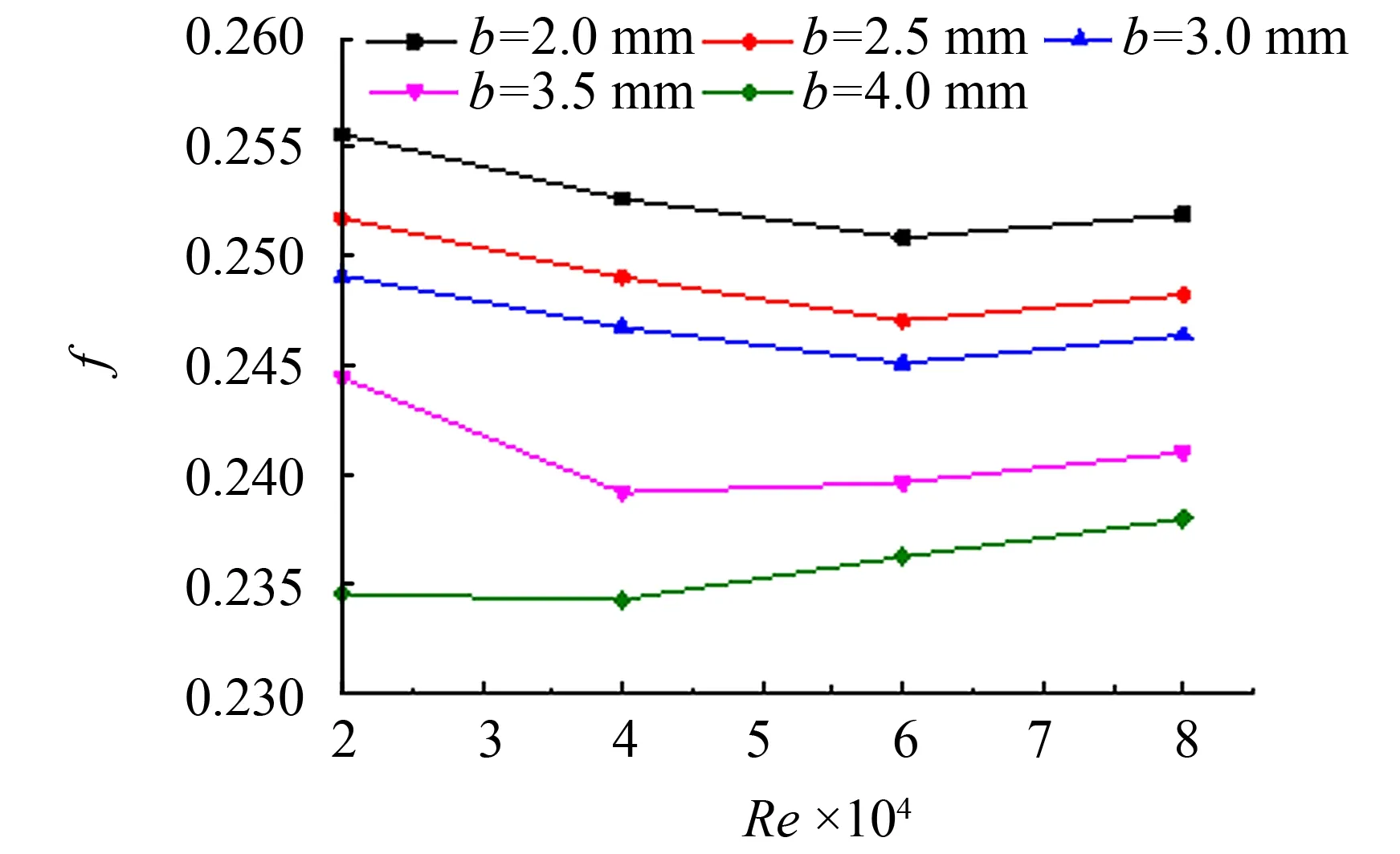
图14 阻力系数与垫条厚度的关系Fig.14 Relationship between drag coefficient and the cushion thickness

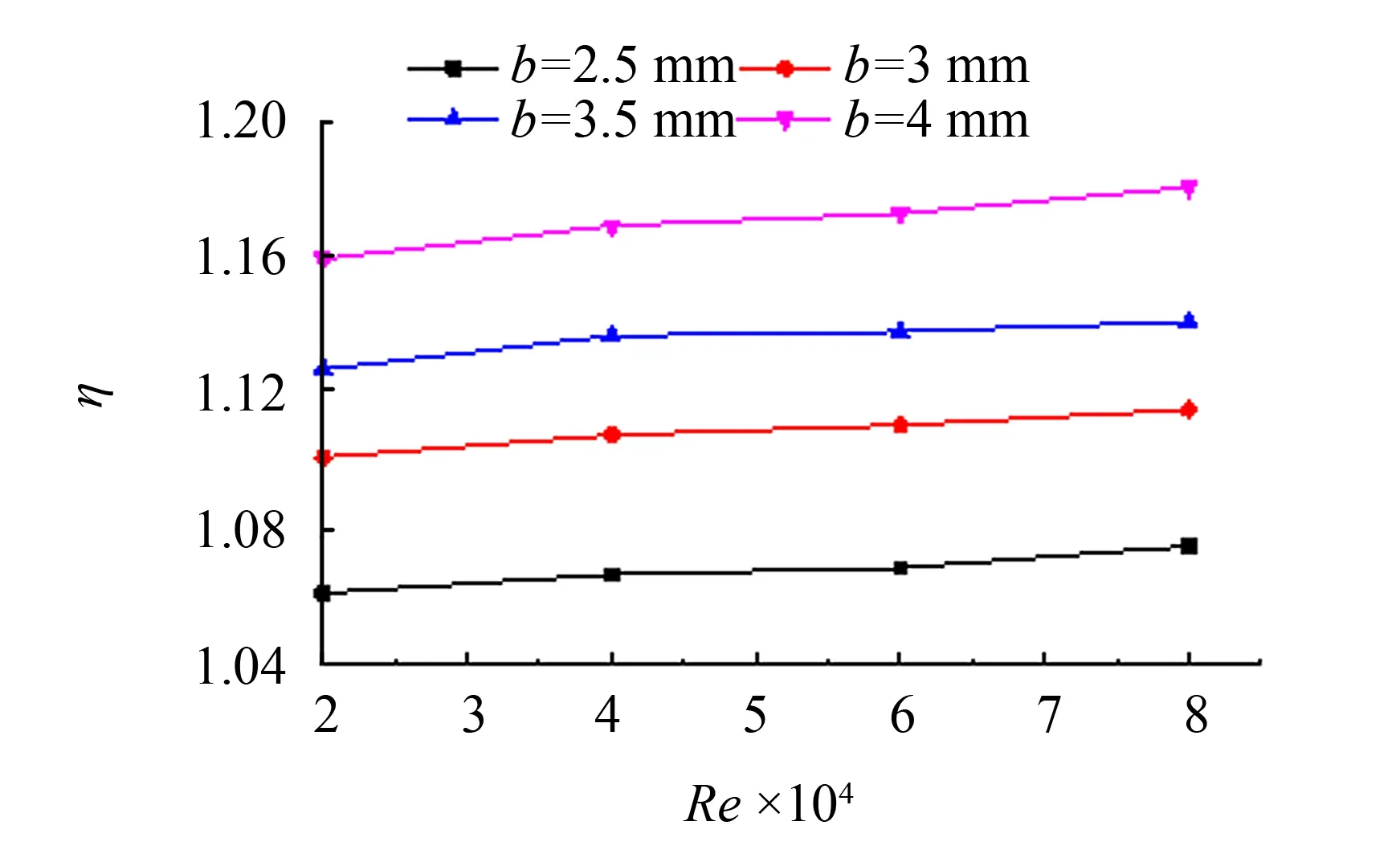
图15 综合性能评价因子与垫条厚度的关系Fig.15 Relationship between comprehensive performance evaluation factor and the cushion thickness

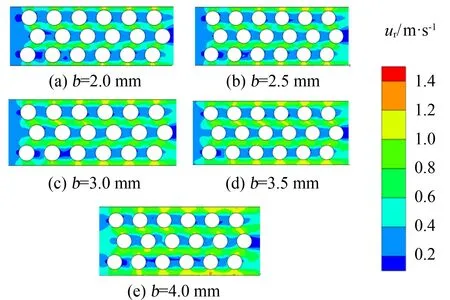
图16 不同垫条厚度的换热器模型的壳程速度云图Fig.16 Shell velocity cloud map of heat exchanger model with different cushion thickness

从壳侧流体流动状态入手分析上述结果的成因， 见图16. 从图16可以看出，Re数为40 000时， 随着垫条厚度从2 mm变化到4 mm， 换热段的平均径向速度先从0.106 1 m·s-1增大至0.110 3 m·s-1， 再减小至0.106 8 m·s-1； 其湍流强度也从0.018 9 J逐渐提高至0.023 0 J后降低至0.022 2 J. 随着垫条厚度增至3 mm以上， 虽然主流受管壁和径向流动的影响减小， 但局部流速增长迅速， 产生了较好的对流换热效果. 随着垫条厚度的增大， 径向流体速度增大； 与此同时， 流通截面最窄处的面积随之增大， 流体流过管束时的文丘里效应减弱， 局部阻力随之减小.

3 结语

利用Fluent软件建立了简化的缠绕管式换热器流体动力学模型， 以此分析不同结构参数对缠绕管式换热器热力学和动力学性能的影响. 将模拟计算得到的Nu数、 单位高度压降与实验结果对比， 其平均相对误差控制在10%左右. 盘管层数的变化会影响阻力系数的大小， 但几乎不影响Nu数； 综合性能评价因子对盘管层数的变化也并不敏感. 随着轴向间距的增加，Nu先略微上升了1.66%后开始保持平稳； 阻力系数则随其增加先略微增加1.76%后快速减小； 综合性能评价因子呈现出与Nu数相同的变化趋势. 当轴向间距增加到8 mm时， 流体的径向流速和湍流动能增大至顶峰， 此种情况下综合性能评价因子也达到最大值. 垫条厚度的增加使壳程流通截面积增大， 流过纵向管间间隙的流体流量增加，Nu数随之升高； 与此同时， 整体阻力系数减小， 进一步加大了综合性能评价因子也随之升高的趋势. 相较盘管层数和轴向间距， 垫条厚度对缠绕管式换热器的换热和流动性能影响更甚， 可作为缠绕管式换热器性能优化的重点方向.

参考文献：

[1] YAN W M, PAN C W, YANG T F,etal. Experimental study on fluid flow and heat transfer characteristics of falling film over tube bundle[J]. International Journal of Heat and Mass Transfer, 2019, 130: 9-24.

[2] ZHAO C Y, JI W T, HE Y L,etal. A comprehensive numerical study on the subcooled falling film heat transfer on a horizontal smooth tube[J]. International Journal of Heat and Mass Transfer, 2018, 119: 259-270.

[3] 李书磊, 鹿来运, 陈杰, 等. 结构参数对缠绕管式换热器管测换热影响模拟研究[J]. 节能技术, 2017, 35(6): 498-504.

[4] LU X, ZHANG G P, CHEN Y T,etal. Effect of geometrical parameters on flow and heat transfer performances in multi-stream spiral-wound heat exchangers[J]. Applied Thermal Engineering, 2015, 89:1104-1116.

[5] WANG S M, JIAN G P, XIAO J,etal. Optimization investigation on configuration parameters of spiral-wound heat exchanger using genetic aggregation response surface and multi-objective genetic algorithm[J]. Applied Thermal Engineering, 2017, 119: 603-609.

[6] WANG S M, JIAN G P, WANG J R,etal. Application of entransy-dissipation-based thermal resistance for performance optimization of spiral-wound heat exchanger[J]. International Journal of Heat and Mass Transfer, 2018, 116: 743-750.

[7] 高兴辉, 周帼彦, 涂善东. 缠绕管式换热器壳程强化传热性能影响因素分析[J]. 化工学报, 2019, 72(7): 1-15.

[8] 尾花英朗. 热交换器设计手册(上册)[M]. 北京: 石油工业出版社, 1981: 5-7.

[9] 吴志勇, 陈杰, 浦晖. LNG绕管式换热器壳侧过热态流动的数值模拟[J]. 煤气与热力, 2014, 34(8): 6-11.

[10] 阳大清, 周红桃. 绕管式换热器壳侧流场流动与传热的数值模拟研究[J]. 压力容器, 2015, 32(11): 40-46.

[11] 黄云云, 黄永曙, 王为旺. 不同截面形状螺旋管流动与传热的数值研究[J]. 计算机与应用化学, 2016, 33(12): 1261-1266.

[12] NEERAAS B O, FREDHEIM A O, AUNAN B. Experimental shell-side heat transfer and pressure drop in gas flow for spiral-wound LNG heat exchanger[J]. International Journal of Heat and Mass Transfer, 2004, 47: 353-361.

[13] 于定勇, 张广成, 马朝晖. 湍流场多柱体绕流形态和水动力特性研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(6): 52-59.