带组合型阻尼器的可更换连梁

蒋欢军，黄有露，李恺轩

（同济大学 土木工程防灾国家重点实验室，上海200092）

现阶段我国的抗震设计思想是“小震不坏、中震可修、大震不倒”，这一思想有效地控制了地震中结构的倒塌和人员伤亡，但大量的震害表明，由于部分主要构件损伤严重，震后修复困难，结构往往只能推倒重建，造成巨大的经济损失[1-2].从20 世纪90 年代开始，基于性能的抗震设计逐渐成为工程抗震的主流方向之一[3]，该方法保证建筑在未来可能发生的地震作用下具有预期的抗震性能和安全度.

2009 年1 月，在美日地震工程第2 阶段合作会议上，美日学者首次提出将“可恢复功能城市”作为未来地震工程合作的大方向[4]，可恢复功能结构逐渐成为国内外学者的研究热点.连梁作为剪力墙肢之间的连接构件，跨高比常小于2，在地震作用下容易形成X 形交叉裂缝，难以实现端部塑性铰耗能从而发生脆性剪切破坏.为此，研究人员提出了可更换连梁的概念，即在连梁中设置可更换消能部件，在地震发生时消耗结构主要的地震能量，保护主体构件不发生破坏[5].若可更换部件在强震中发生破坏，在震后更换方便，则可实现建筑功能的快速恢复.

国内外学者提出了多种形式的可更换连梁.2007 年克莱姆森大学的Fortney 等[6]提出部分削弱工字钢连梁腹板的厚度，制成可更换连梁保险丝.2009 年韩国檀国大学的Chung 等[7]提出在钢连梁中部附加一个摩擦阻尼器，通过摩擦阻尼器来增强连梁的耗能能力.进一步研究表明，将不同耗能机制的耗能部件组合在一起，可以发挥各自的优势从而提升耗能能力.2015 年同济大学的朱奇云、吕西林[8]提出了一种新型橡胶-软钢复合耗能器，在小变形状态下，剪切钢板带动黏弹性材料发生剪切变形；在大变形状态下，软钢发生剪切变形耗能.

带金属阻尼器的传统连梁耗能能力强，但在小震和风振作用下阻尼器处于弹性状态，无法起到耗能作用；黏弹性阻尼器在很小的位移下即开始耗能，但抗侧刚度较小，单独使用时耗能能力较弱.因此，本文提出了一种带O 型钢板-黏弹性组合型阻尼器的新型可更换连梁，该组合型阻尼器在风振和不同水准地震作用下均能发挥消能减震作用，震后便于拆卸更换.给出了组合型阻尼器的构造形式和力学性能计算公式，并进行了阻尼器的低周反复加载试验，进一步提出了带新型可更换连梁结构的设计方法.通过对带新型可更换连梁与带传统钢筋混凝土连梁的超高层结构在风荷载和地震作用下反应的对比分析，验证结构的抗风和抗震性能.

1 带组合型阻尼器的可更换连梁

1.1 组合型阻尼器组成

组合型阻尼器由一块O 形钢板阻尼器和一块黏弹性阻尼器并联而成，通过O 型钢板弯曲变形和黏弹性阻尼器剪切变形的耗能机制协同耗能.O 形钢板-黏弹性组合型阻尼器的组成和在连梁中的连接形式如图1 所示.其中O 型钢板阻尼器是将一块钢板弯曲成“O”形并焊接成一体，沿厚度方向在左右两端与外部钢板连接；黏弹性阻尼器是由约束钢板和中间钢板夹着两层黏弹性材料层组成，二者通过高温硫化作用紧密连接，再通过高强螺栓或焊缝连接外部钢板.

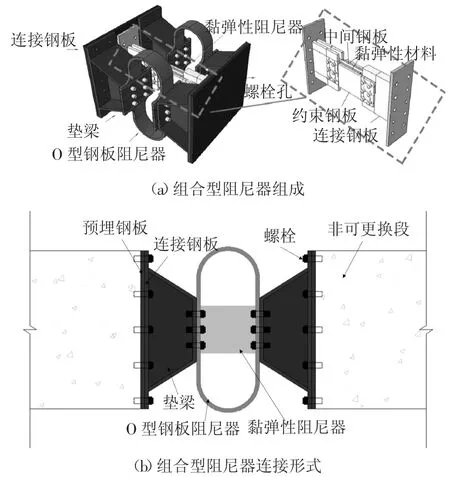
图1 可更换连梁示意图Fig.1 Schematic drawing of replaceable coupling beam

O 型钢板阻尼器由两块U 型钢板通过中部扩大连接板并联而成，连接板属于构造构件，对O 型钢板阻尼器力学性能的影响可以忽略不计，因此由对称性对O 型钢板阻尼器的半边结构进行分析.U 型钢板的平面外变形会受到梁的约束限制，仅在圆弧段发生平面内弯曲变形，根据结构力学中的力法相关知识[9]，可得到如下O 型钢板阻尼器的主要力学性能计算公式：

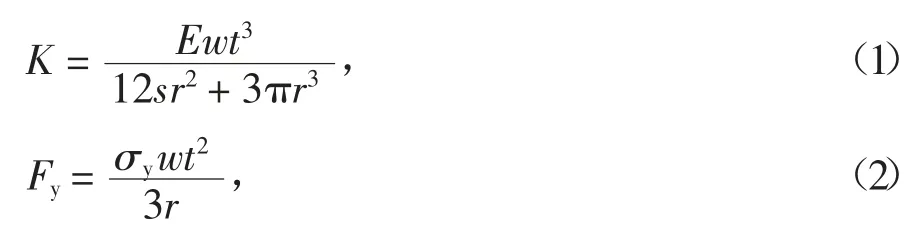
式中：K、Fy、uy分别为O 型钢板阻尼器的初始刚度、屈服承载力和屈服位移；t、w、r、s 分别为钢板厚度、钢板宽度、圆弧段半径和平直段长度；σy为钢板弯曲时截面应力；E 为材料的弹性模量.

对于黏弹性阻尼器，采用Shen 等[10]提出的等效刚度模型，计算公式如下：

式中：G1为黏弹性材料的储能剪切模量；n、A、t 分别为黏弹性材料层数、剪切面积和厚度；Keq为等效刚度.

可更换连梁由三部分组成：中间段为可更换的组合型阻尼器，左、右两段均为型钢混凝土梁.可更换段与左右两段均采用螺栓连接，便于震后更换.

1.2 阻尼器试验结果

为研究黏弹性阻尼器、O 型钢板阻尼器以及二者并联形成的组合型阻尼器的力学性能和耗能能力，分别对3 种阻尼器进行了低周反复加载试验并对试验结果进行分析.

黏弹性阻尼器的剪切面积取为4×104mm2，材料层层数为2 层，厚度为16 mm，采用应变幅值逐渐增大的正弦循环位移加载方式，试件加载照片和试验得到的滞回曲线如图2 所示.从图2 中可看出，黏弹性阻尼器在很小的位移下即开始耗能，耗能能力良好.在该设计参数下，当加载至150%剪切应变时，黏弹性阻尼器的最大剪力可达到132 kN.

图2 黏弹性阻尼器试验Fig.2 Test of viscoelastic damper

设计一个并联式O 型钢板阻尼器，其中单个O型钢板阻尼器的设计参数取为22 mm×160 mm×150 mm×120 mm（t×w×r×s）.再将同尺寸参数的黏弹性阻尼器与并联式O 型钢板阻尼器组合，形成O 型钢板-黏弹性组合型阻尼器.对两种阻尼器在小变形和大变形状态下的耗能性能进行试验研究，现场照片如图3 所示.

图3 现场试验Fig.3 Field test of damper

并联式O 型钢板阻尼器试验采用位移控制加载制度，组合型阻尼器试验采用应变幅值逐渐增加的正弦循环位移加载制度，得到的滞回曲线对比如图4所示.从图中可知，当剪切位移较小时，并联式O 型钢板阻尼器基本处于弹性状态，没有形成滞回环，而组合型阻尼器由于黏弹性阻尼器在很小的变形下即可耗能，滞回环面积较大，耗能性能良好.

图4 小变形状态下滞回曲线Fig.4 Hysteretic curves under small deformation

随着加载位移逐渐增大，两种阻尼器的滞回环面积逐渐增大，耗能性能稳定，滞回曲线对比如图5所示.从图中可知，当加载位移达到66 mm 时，由于组合型阻尼器中的黏弹性材料部分与钢板分离，峰值承载力迅速下降，而此时并联式O 型钢板阻尼器仍具有稳定的承载能力和耗能能力.当加载位移达到88 mm 时，黏弹性材料层与钢板完全脱离，组合型阻尼器的承载能力完全由O 型钢板阻尼器承担，二者的滞回曲线基本重合.

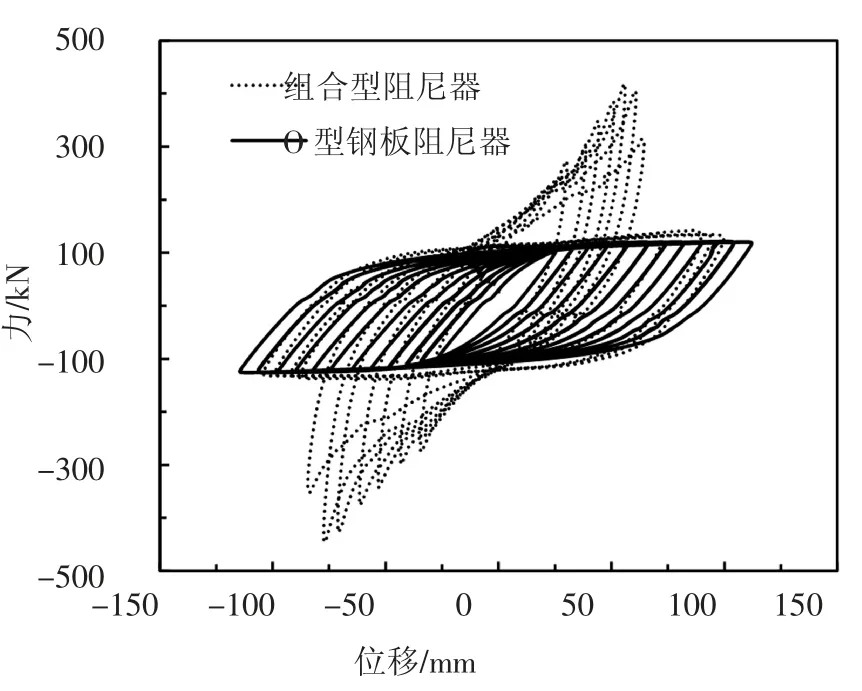
图5 大变形状态下滞回曲线Fig.5 Hysteretic curves under large deformation

1.3 设计方法

为减轻传统连梁在地震作用下的破坏，实现建筑结构震后可更换、快速修复的要求，可更换连梁的设计要求如下：在风荷载和小震作用下，O 形钢板阻尼器处于弹性状态，黏弹性阻尼器工作、耗能；在中震和大震作用下，O 型钢板阻尼器屈服，与黏弹性阻尼器共同耗能.

采用组合型阻尼器与传统钢筋混凝土连梁等强度的设计原则.对传统钢筋混凝土连梁，当采用对称配筋且无斜筋时，其正截面抗弯及抗剪承载力按下列公式计算[11]：

式中：Mc为截面抗弯承载力；Vc1、Vc2为截面抗剪承载力；γRE为钢筋混凝土构件承载力抗震调整系数，梁受弯、受剪时分别取为0.75、0.85；fy、fyv分别为纵筋和箍筋的抗拉强度设计值；ft、fc分别为混凝土轴心抗拉、抗压强度设计值；As为单侧受拉纵向钢筋截面面积；a′s为受压区纵向钢筋合力点至截面受压边缘的距离；h0为截面有效高度；b 为截面宽度；Asv为箍筋截面面积；s 为箍筋间距；βc为混凝土强度影响系数，当混凝土强度等级不超过C50 时取1.0.

可更换段中组合型阻尼器的抗剪承载力设计值应满足式（8）要求.

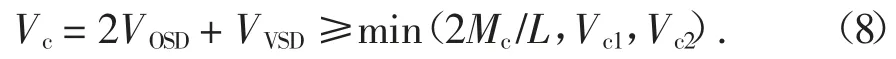
式中：VOSD为O 型钢板阻尼器的抗剪承载力；VVSD为黏弹性阻尼器的抗剪承载力；L 为传统钢筋混凝土连梁长度.

O 型钢板阻尼器屈服后刚度较小，而黏弹性阻尼器在150%剪切应变内的刚度变化不大.基于阻尼器试验得到的峰值剪力计算结果，给出黏弹性阻尼器的抗剪承载力占截面总剪力的1/3～1/2，其余剪力由O 型钢板阻尼器承担.

组合型阻尼器的抗剪刚度相比传统钢筋混凝土连梁的刚度较小，在确定组合型阻尼器的设计参数后需验算结构在多遇地震下的层间位移角是否满足规范限值要求.

对于连梁的可更换段长度，涉及到墙肢与连梁的转动能力及可更换段自身的变形能力.可更换段竖向位移可按式（9）计算.

式中：d、Lf分别为可更换段竖向位移和长度；Lwall为联肢剪力墙墙肢形心之间的距离；γ 为可更换段转角；θ 为结构层间位移角.

为保证组合型阻尼器满足设计目标，O 型钢板

阻尼器和黏弹性阻尼器需分别满足下式要求：

式中：θe、θp分别为结构的弹性和弹塑性层间位移角限值；t 为黏弹性材料层厚度；uy为O 型钢板阻尼器的屈服位移.

1.4 设计流程

实际工程中，对于设置可更换连梁的位置确定是十分重要的，最直接的方法是通过结构的弹性反应谱分析确定内力较大的连梁进行替换.一般在高层建筑中，结构总高度1/3 位置处连梁的内力最大[12]，往往容易超筋，可设计为可更换连梁.带组合型阻尼器的新型可更换连梁的基本设计步骤如下：

1）根据结构已有信息，对带传统连梁的结构进行弹性反应谱分析，确定内力较大的连梁，将这些连梁作为新型可更换连梁进行设计.

2）根据可更换连梁的位置信息，由公式（9）（10）（11）分别确定可更换段长度Lf、O 型钢板阻尼器的屈服位移uy和黏弹性阻尼器材料层厚度t.

3）根据确定的O 型钢板阻尼器的屈服位移uy，由公式（3）初步确定O 型钢板阻尼器的尺寸参数t、w、r、s（分别为钢板厚度、钢板宽度、圆弧段半径和平直段长度）.

4）选定适当的剪力承担比例，根据原连梁的抗剪承载力计算公式（8）分别确定黏弹性阻尼器抗剪承载力VVSD和O 型钢板阻尼器抗剪承载力VOSD.

5）选择黏弹性阻尼器的构造形式和黏弹性材料（确定黏弹性材料的层数n、储能剪切刚度G1），根据确定的抗剪承载力VVED和最大竖向位移dmax由公式（4）确定黏弹性材料的剪切面积A.

6）根据确定的O 型钢板阻尼器抗剪承载力VOSD（等于Fy），由公式（2）进一步优化O 型钢板阻尼器设计参数.

7）采用数值模拟方法对带可更换连梁的结构再进行弹性反应谱分析，验算层间位移角是否满足规范要求，若满足要求，则结束设计，否则回到步骤4）重新设计.

2 超高层结构计算模型

2.1 模型参数

本文作者课题组设计了一个50 层带有传统钢筋混凝土连梁的超高层型钢混凝土框架-混凝土核心筒Benchmark 模型[13]（简称CBM），标准层的结构平面布置如图6 所示.

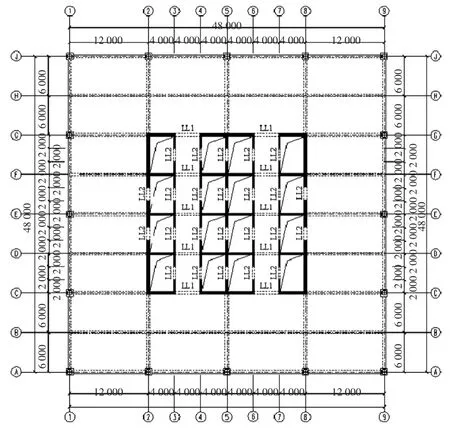
图6 标准层的结构平面布置Fig.6 Structural plan layouts of typical floor

结构底层层高为6 m，其余楼层层高为4.5 m，总高度为226.5 m.抗震设防烈度为8 度（0.2 g），场地类别为Ⅲ类，设计分组为第1 组，特征周期为0.45 s，基本风压为0.55 kN/m2，场地粗糙度类别为C 类.型钢混凝土柱和核心筒的混凝土强度等级为C60，楼板的混凝土强度等级为C35，钢材强度等级均为Q345；连梁的混凝土强度等级为C60，截面高度为750 mm，宽度与墙厚相同，随结构高度的增加而减小.楼面及屋面恒载均为4 kN/m2，楼面活载为3 kN/m2，屋面活载取0.5 kN/m2.

2.2 可更换连梁设计

带新型可更换连梁的结构模型简称为NBM.由CBM 正交两个方向的弹性反应谱分析可知，11～20层两个方向的连梁内力均较大，考虑经济性和NBM的抗侧刚度，对CBM 11～20 层之间所有X 方向的连梁进行更换，每层10 根，共计100 根；对CBM 11～20层之间Y 方向中部的两排连梁进行更换，每层14根，共计140 根.根据可更换连梁的设计流程，确定的O 型钢板和黏弹性阻尼器设计参数见表1.

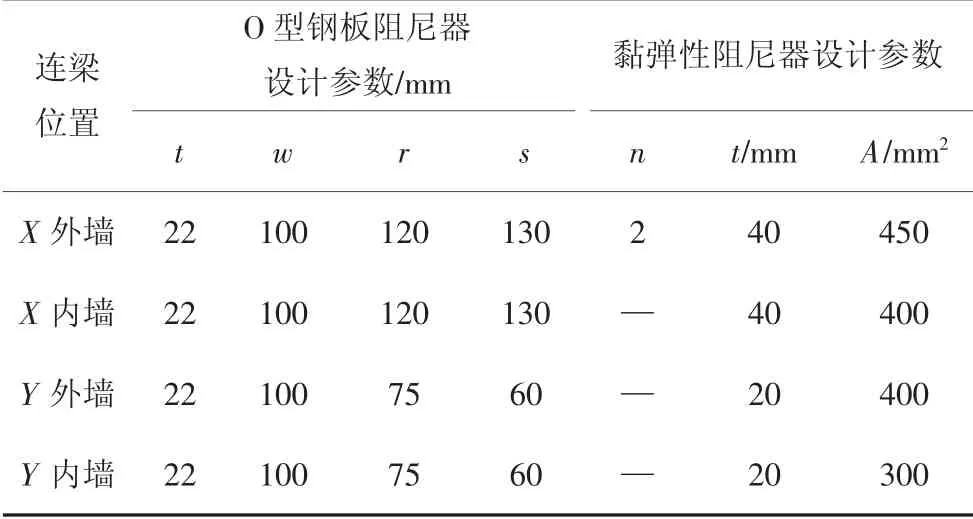
表1 O 型钢板阻尼器和黏弹性阻尼器设计参数Tab.1 Design parameters of O-shaped steel plate damper and viscoelastic damper

2.3 计算模型

对于材料的应力-应变关系，型钢和钢筋均采用双折线模型，对不同类型的构件混凝土的本构关系选择不同.外框架中的型钢混凝土柱和剪力墙中的约束边缘构件的箍筋配置较多，对混凝土的约束作用明显，使用考虑箍筋约束效应的Mander 模型[14]；连梁、楼板和剪力墙中非约束边缘构件的墙体使用《混凝土结构设计规范》（GB 50010—2010）中建议的本构模型.使用Perform-3D 有限元软件建立结构的计算模型.

梁、柱、剪力墙分别选择Beam Element、Column Element、Shear Wall Element，采用纤维截面进行模拟.需要指出的是，Perform-3D 中没有可直接用来模拟SRC 柱的单元，实际建模过程中，可以将SRC 柱中的型钢纤维通过面积等效的方法离散成钢筋纤维.对黏弹性阻尼器，参照多伦多大学Lyons 建立的Kelvin-Voigt 模型[15]，并通过并联一个提供刚度的弹性杆及提供黏滞力的Fluid 单元达到拟合效果.对O型钢板阻尼器，取一个位移相关型剪切铰提供剪力，通过与剪切铰串联的钢梁单元提供抗剪刚度及轴向刚度.

2.4 模态分析

通过结构的模态分析，可得到结构基本动力特性.对比发现NBM 和CBM 的模态振型完全一致，前3 阶模态的对比见表2.从表2 中可看出，由于11～20 层X 方向的连梁全部替换成可更换连梁，因此结构的整体刚度有所削弱，第一周期增大了8.65%，Y方向的连梁做了部分替换，周期增大了5.2%，第三振型即扭转周期增大了16%，对结构的Z 向振型及局部振型周期没有影响.结构扭转为主的第一自振周期与平动为主的第一自振周期之比满足规范限值0.85 的要求.

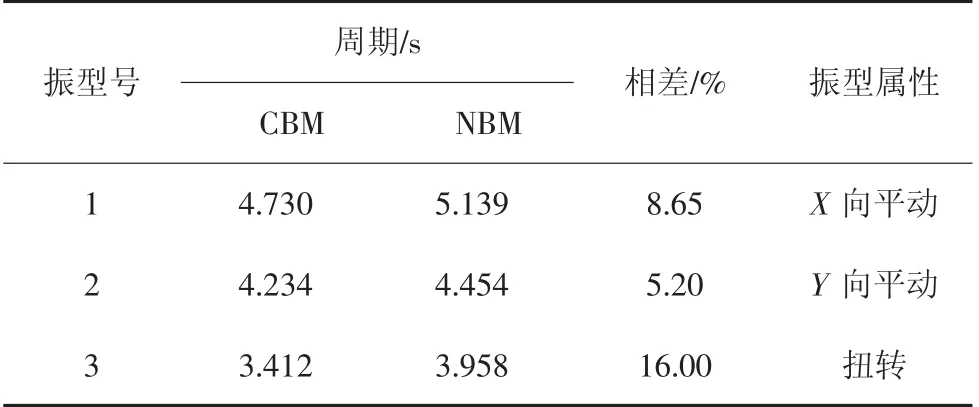
表2 CBM 和NBM 前3 阶模态周期对比Tab.2 Comparison of modal periods of the first 3 modes between CBM and NBM

2.5 反应谱分析

对CBM 和NBM 进行8 度小震作用下的弹性反应谱分析，层间位移角计算结果如图7 所示.从图中结果可知，由于NBM 11～20 层设置了可更换连梁，层间位移角增大，X、Y 方向层间位移角最大增幅分别达到41.42%、39.13%，但仍满足规范规定的弹性层间位移角限值1/549（线性内插得到）的要求.此外，NBM 和CBM 相比，最大层间位移角所在的楼层位置也发生了变化.

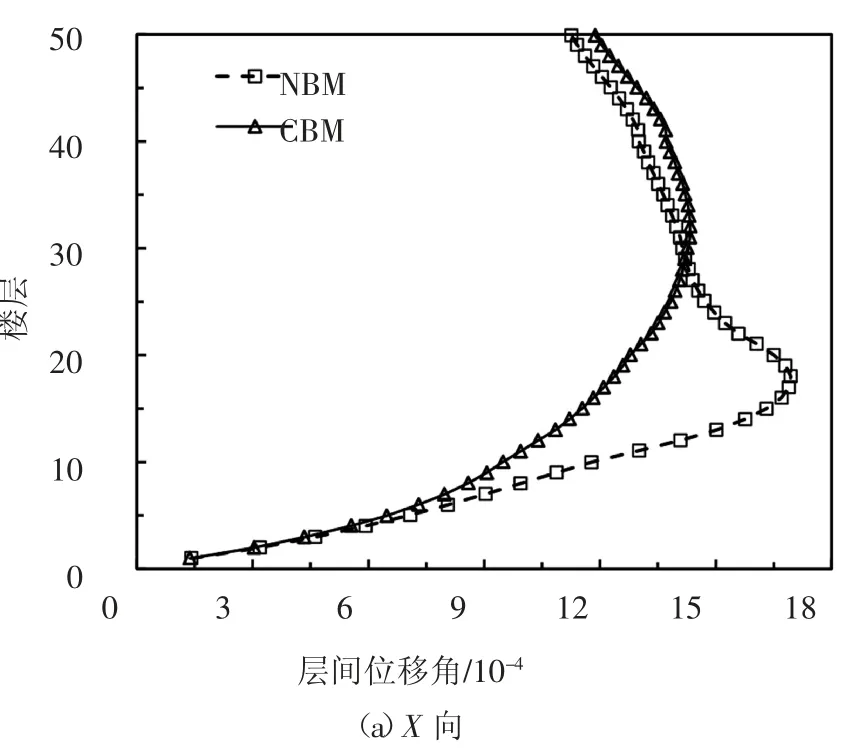
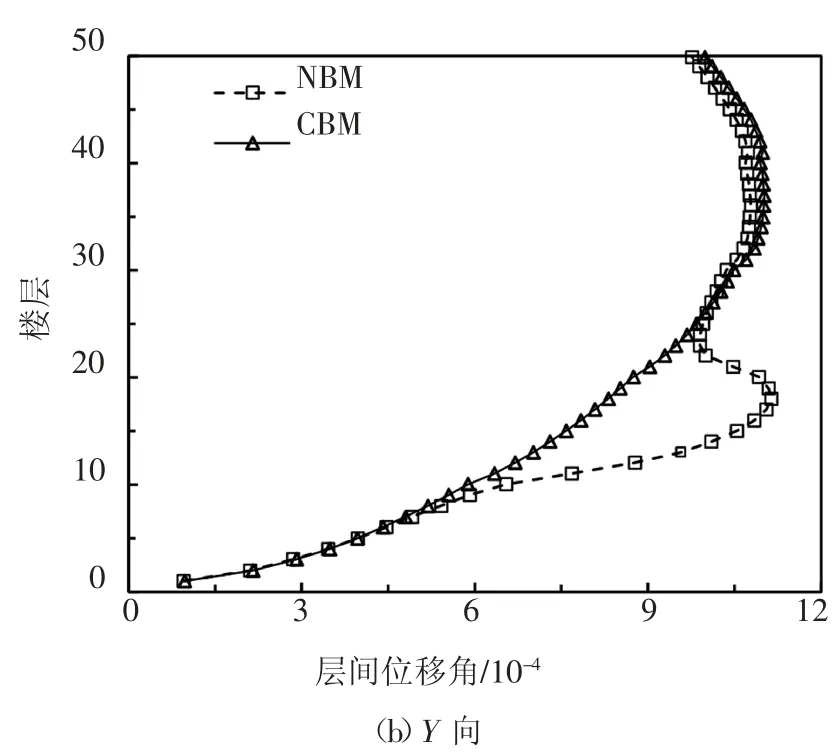
图7 两种结构层间位移角对比Fig.7 Comparison of inter-story drift ratio between two kinds of structures

3 弹塑性时程分析

3.1 地震波选取

结合场地条件和结构动力特性，选择5 条天然波和2 条人工波共计7 条地震波作为输入地震波，其中4 条天然地震波来自PEER 强震记录数据库，另外1 条天然地震波为汶川波.地震波采用双向输入，两个方向输入加速度幅值之间的比例关系为1∶0.85，多遇地震和罕遇地震作用下的加速度峰值分别为70 gal、400 gal.选取的地震波信息见表3.各条地震波的加速度反应谱与规范设计反应谱的对比如图8 所示.

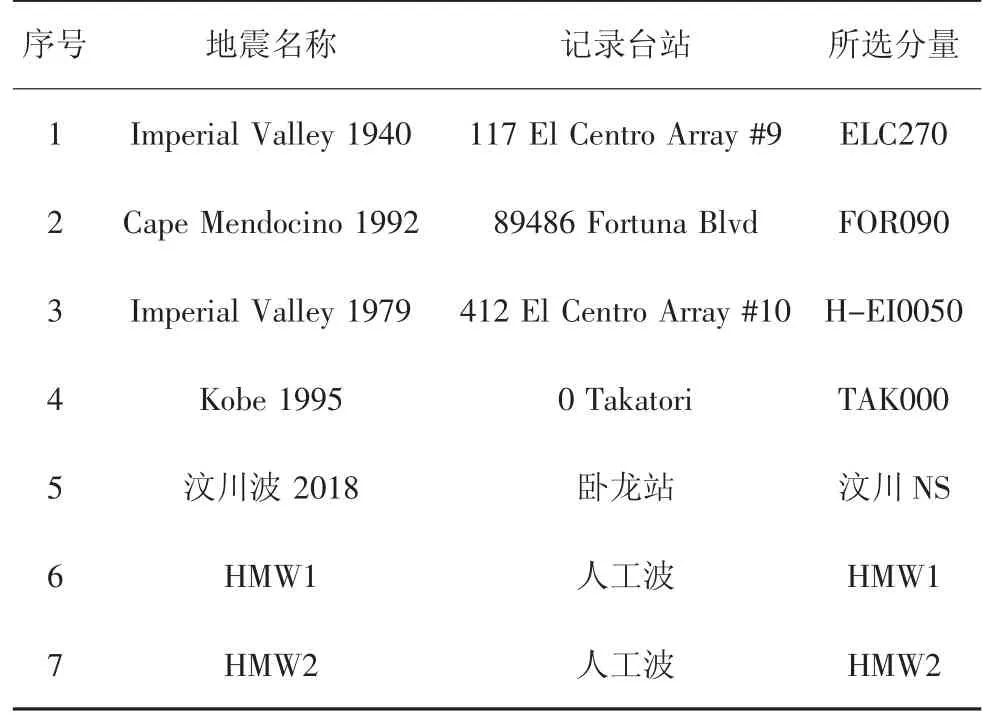
表3 地震波信息Tab.3 Seismic wave information

图8 地震波反应谱及规范设计反应谱对比Fig.8 Comparison of acceleration spectra of earthquakes with code design spectrum

3.2 地震时程分析结果

3.2.1 层间位移角

表4 列出了两个结构在多遇地震和罕遇地震作用下最大层间位移角的对比结果.整体而言，在多遇地震作用下，NBM 的最大层间位移角大于CBM，主要原因在于可更换连梁的刚度小于普通钢筋混凝土连梁，NBM 的抗侧刚度小于CBM，两个结构的平均层间位移角均满足规范限值1/549 的要求.NBM 的最大层间位移角增加不多，平均增大2%.

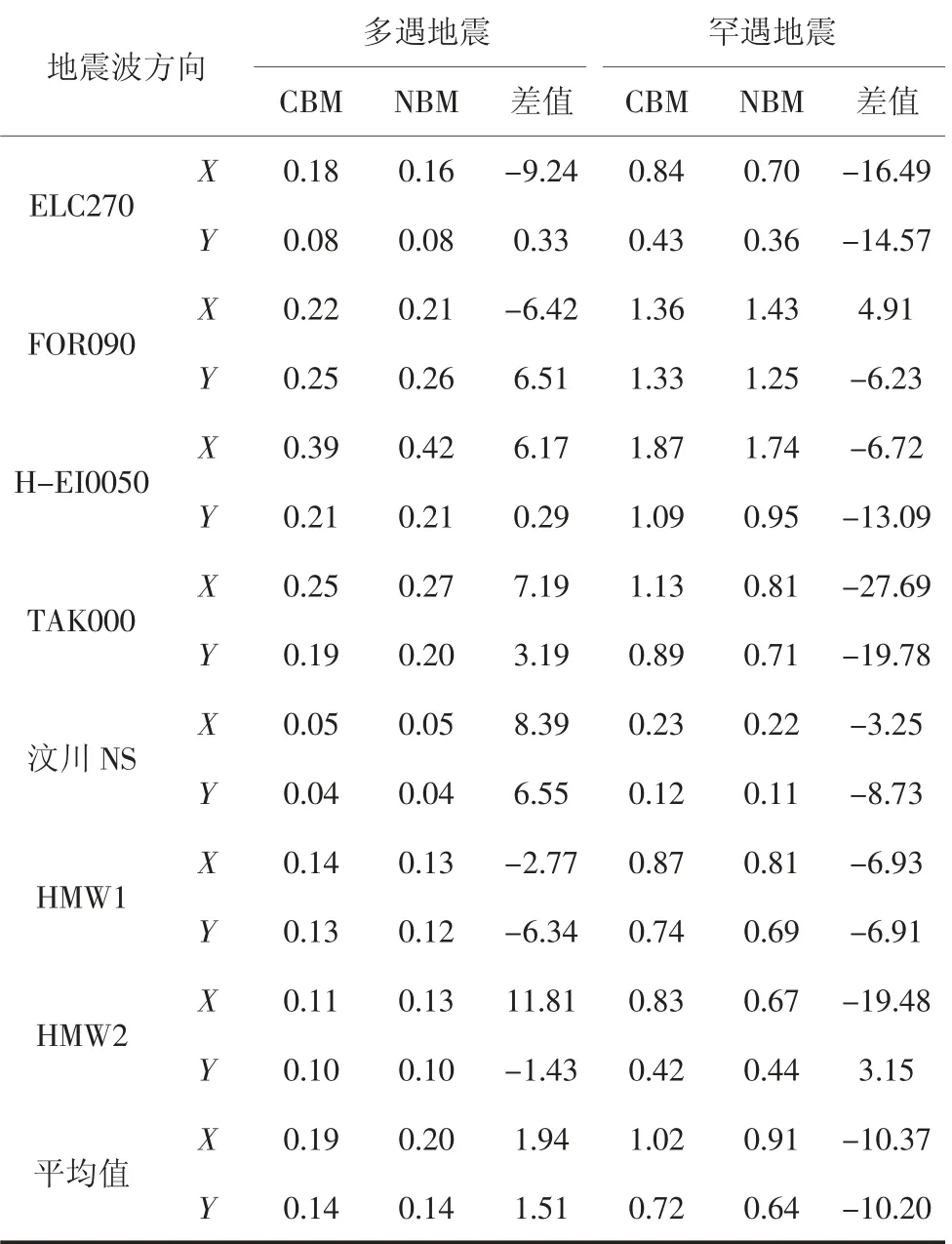
表4 结构层间位移角最大值Tab.4 Maximum inter-story drift ratio %

在罕遇地震作用下，整体而言，NBM 的最大层间位移角小于CBM，特别是在ELC270 波、H-EI0050波和TAK000 波作用下，层间位移角控制效果显著.NBM 的最大层间位移角平均比CBM 减小10%. 此时NBM 的平均层间位移角满足规范限值1/100 的要求.

3.2.2 阻尼器耗能性能

限于篇幅，以NBM 第15 层的外墙连梁为例，分析其在多遇地震和罕遇地震作用下设置的O 型钢板和黏弹性阻尼器在TAK000 波作用下的滞回曲线，如图9、图10 所示.

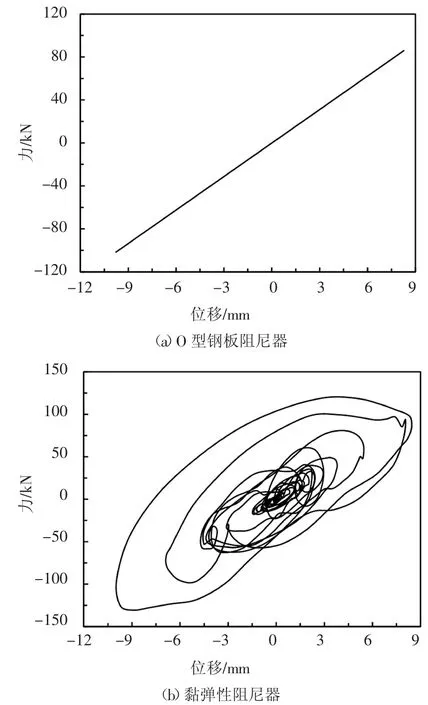
图9 多遇地震作用下滞回曲线Fig.9 Hysteretic curves under frequent earthquakes

在多遇地震作用下，O 型钢板阻尼器荷载-位移曲线为直线，钢板未发生屈服，处于弹性状态，刚度较大.黏弹性阻尼器滞回曲线饱满，呈典型的椭圆形状，在很小的位移下即开始耗能.

在罕遇地震作用下，O 型钢板阻尼器进入塑性耗能，滞回曲线近似为平行四边形，耗能性能稳定，屈服后刚度较小.黏弹性阻尼器滞回曲线饱满，继续发挥耗能能力，减小了主体结构消耗的地震能量，从而更好地保护了主体结构.

图10 罕遇地震作用下滞回曲线Fig.10 Hysteretic curves under rare earthquakes

3.2.3 损伤情况

在罕遇地震作用下，NBM 的剪力墙损伤明显小于CBM，尤其是在ELC270 波、H-EI0050 波和TAK000 波作用下，可更换连梁充分发挥耗能性能，减轻主体结构的损伤. 图11 所示为在地震波TAK000 作用下，NBM 和CBM 的剪力墙混凝土损伤情况对比，不同颜色代表了剪力墙混凝土出现的最大应变与混凝土极限压应变的比值.可以看出NBM底部剪力墙墙肢的损伤相对较大，出现受压损伤的剪力墙墙肢分布楼层较CBM 大体不变，但损伤水平有明显降低.

3.3 风荷载响应分析

本算例结构高226.5 m，需按规范要求进行风荷载作用下的舒适度验算.Perform-3D 软件中无法直接定义风荷载，因此需要对风荷载作用进行等效模拟. 具体的方法是根据外立面风荷载体型系数将Benchmark 模型分为5 段，将每一段的风压时程乘以受风面积等效成为均匀分布在该段的节点力的时程，再通过定义节点力的时程实现风荷载的施加.

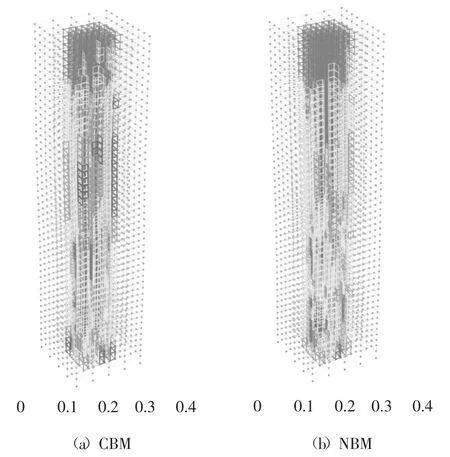
图11 罕遇地震下剪力墙混凝土损伤对比Fig.11 Comparison of damage condition of concrete in shear walls under rare earthquakes

结构每一段的风压时程来源于相应的风速时程，对于任意一点的风速时程，一般包括平均风和脉动风两个部分.首先计算结构各段代表点的平均风速，再根据李杰等[16]提出的脉动风速随机Fourier 谱模型生成脉动风速时程，将二者叠加后得到各点的风速时程. 《建筑结构荷载规范》（GB 50009—2012）中给出了风压ω 和风速v 的换算公式：

式中：ρ 为空气密度.

3.3.1 阻尼器滞回曲线

仍以NBM 第15 层外墙连梁为例，分析其在风荷载作用下O 型钢板和黏弹性阻尼器的滞回曲线，如图12 所示.可看出，在风荷载作用下O 型钢板阻尼器荷载-位移曲线保持直线，处于弹性状态；黏弹性阻尼器在较小的位移下即开始耗能，滞回环面积不断增大，在风荷载作用下呈现出良好的耗能性能.

3.3.2 加速度反应

两个结构两个方向各层的加速度峰值反应如图13 所示.从图中可看出，相比CBM，NBM 在X 和Y两个方向多数楼层的加速度峰值有明显降低.

图12 风荷载作用下阻尼器滞回曲线Fig.12 Hysteretic curves of damper under wind

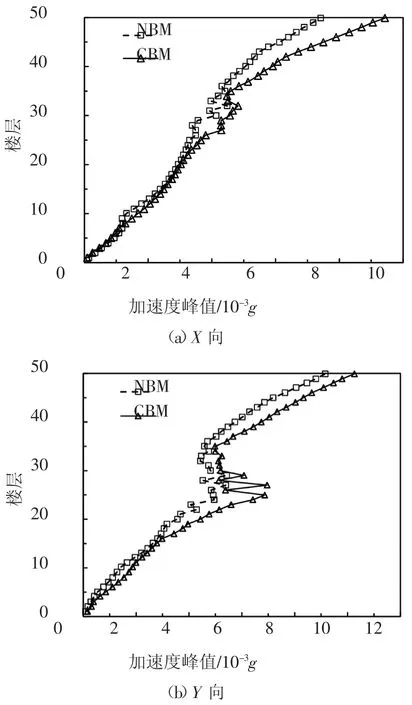
图13 结构各层加速度反应峰值Fig.13 Peak acceleration of each story of structure

两个结构顶层的加速度时程如图14 所示，X 方向和Y 方向最大值分别减小10%和16%.两个结构均满足规范限值0.15 m/s2的要求.

图14 结构顶层加速度时程Fig.14 Time history of acceleration at the top of structure

4 结 论

本文提出了一种带O 型钢板-黏弹性组合型阻尼器的可更换连梁，对组合型阻尼器进行了低周反复加载试验，建立了带可更换连梁结构的设计方法并进行了算例分析.通过上述研究，可获得如下主要结论：

1）试验结果表明，黏弹性阻尼器在很小的位移下即开始耗能，耗能性能良好.并联式O 型钢板阻尼器在位移较小时没有形成滞回环，在大变形状态下耗能性能稳定.组合型阻尼器将O 型钢板阻尼器和黏弹性阻尼器的优点结合，在风振和不同水准地震作用下均能发挥消能减震作用.

2）提出的带O 型钢板-黏弹性组合型阻尼器的可更换连梁设计方法是基于强度等效的原则.带组合型阻尼器的可更换连梁相比于传统混凝土连梁刚度较小，因此将部分传统连梁替换成可更换连梁后，结构的整体刚度会有所下降.

3）在多遇地震作用下，O 型钢板阻尼器处于弹性状态，黏弹性阻尼器开始耗能，NBM 的层间位移角略大于CBM.在罕遇地震作用下，O 型钢板阻尼器屈服与黏弹性阻尼器协同耗能，NBM 的层间位移角和剪力墙损伤明显小于CBM.在风荷载作用下，O 型钢板阻尼器始终保持弹性，黏弹性阻尼器在很小的位移下即开始耗能.相比CBM，NBM 的多数楼层的加速度反应有明显降低.