随机生成空间坐标系的数学分析和实现

贺京杰

（北京电影学院 未来影像高精尖创新中心,北京100088）

1 引言

本实验室开发摄影机器人为PRRPR-S 型双冗余度机器人,主要用于摄像机的运动控制。由于冗余机器人位置级运动学反解有无穷个,故优化反解算法不唯一,且优化结果不稳定。对于不同的反解算法,需要测试算法是否可以收敛,算法的运行速度以及收敛程度。通过一定精度的遍历算法,可确定单个目标位姿全局最优解的所在小区间。以此为基准,可判定其他算法的收敛效果。算法效率的验证,一般采用实验例。在位置级空间中,第一种实验例是目标位姿,即使用不同的算法反解同一个特定的目标位姿；第二种实验例是目标轨迹,但是轨迹只是工作空间的一个较小子集。位置级实验例方法在一定程度上可以了解算法性能,但是缺少对完整工作空间的全面认识。

在速度级空间中,除了上述两种位置级空间的实验例形式外,还有一种实验例是目标球面,即在选定机器人初始状态后,以当前末端点为圆心,半径为r的球面上以平均分布概率选取目标方向。这种方案主要用于速度级反解性能评价,无法全面反应位置级目标空间。

面向完整工作空间的位置级算法性能描述主要有三种方式:第一种是人为设置多目标位姿样本,使其尽可能布满工作空间,由于本机型工作空间大,不仅有位置信息,还有姿态信息,故该方法无法在较短时间内得到全面性结果,如果人为设置少量目标位姿样本,测试方法有失全面性；第二种是通过数学论证,该方法可以精确描述反解算法性能,但是缺少对性能直观感受；第三种采用蒙特卡洛法,即在工作空间内随机生成多个目标位姿样本,记录不同算法的结果空间距离,通过统计计算判定算法性能,该方法具有直观性和一定程度的全面性。但是目前只有随机生成位置目标样本的算法。本文基于蒙特卡洛法,详细论述随机生成位姿目标样本(空间坐标系)的数学分析,通过编写程序在摄影机器人工作空间中生成随机位姿样本空间,为位置级运动学反解算法评价提供目标空间的全面描述。

本文第2部分论述了如何生成一个随机三维坐标系。首先给定坐标系的数学描述,之后按照重要度排序,考虑向量之间的约束关系,依次对坐标系原点、关键姿态轴、第二关键姿态轴以及第三姿态轴进行数学分析。同时有推论结果与实际情况匹配,佐证论述的正确性。第3部分通过计算机编程,在摄影机器人工作空间内随机生成了多目标位姿样本。第4部分对文章进行了总结。

2 笛卡尔坐标系随机生成数学分析

设N、O 和A 分别是坐标系X 轴、Y 轴和Z轴的单位向量,P为坐标系原点位置。记,

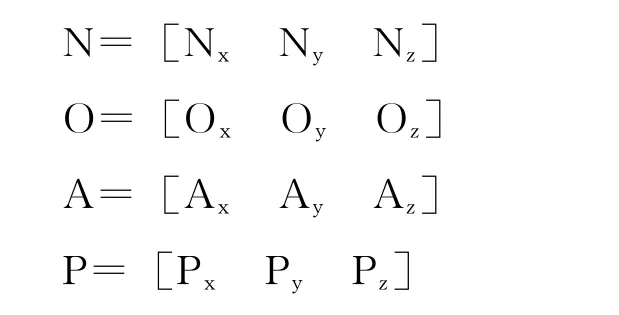
则用4×4矩阵表示空间坐标系。记,

随机生成笛卡尔坐标系过程分为四步。第一步,随机生成坐标系原点位置；第二步,随机生成关键姿态向量A；第三步,随机生成姿态向量N；第四步,随机生成姿态向量O。

2.1 随机生成坐标系原点位置

坐标系原点位置的三个坐标之间没有约束条件,只需要控制原点坐标在工作空间约束范围内随机选取。

2.2 随机生成关键姿态向量A

摄影机器人应用环境中,摄像机的拍摄方向为关键方向,用Z轴的单位向量A 表示。

约束1:A 向量长度为1。有,

在满足式 (1)时,随机确定A。由于A和A尚未确定,有,

选定A后,随机确定A,在满足式 (1)时,有,

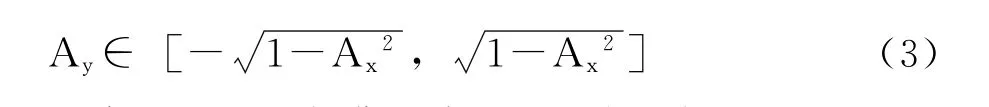
选定A后,在满足式(1)时,有,

其中,A正负值各有50%的选择概率。

2.3 随机生成姿态向量N

在确定Z轴单位向量A 之后,X 轴单位向量N必过P点,且与Z轴垂直。所以X 轴只有一个自由度。只要确定一个参数,X 轴就确定。

约束1:N 向量与A 向量相互垂直。有,

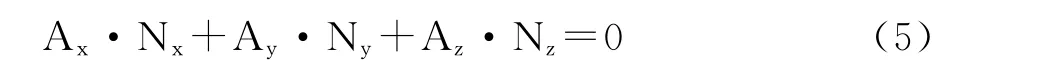
约束2:N 向量长度为1。有,

当A≠0时,在满足式(5)条件下,有,

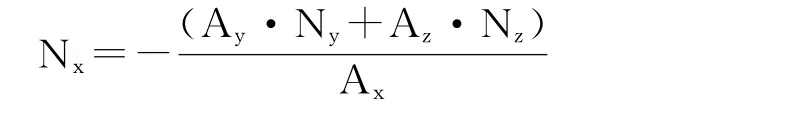
代入式(6),有,

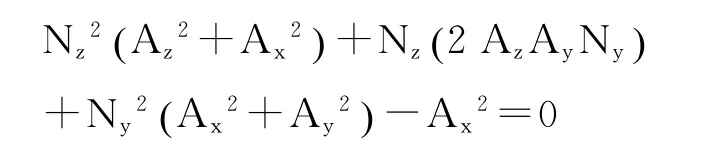
整理得,

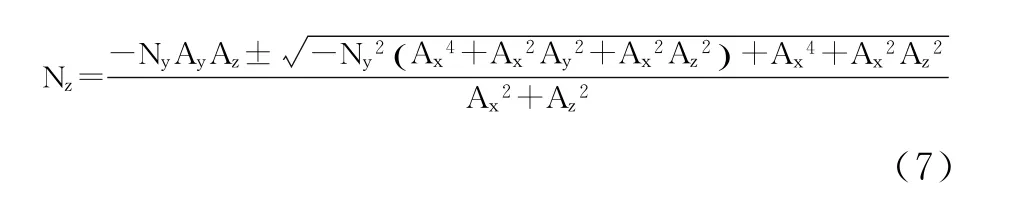
为保证N有实数解,根号内参数有限制,

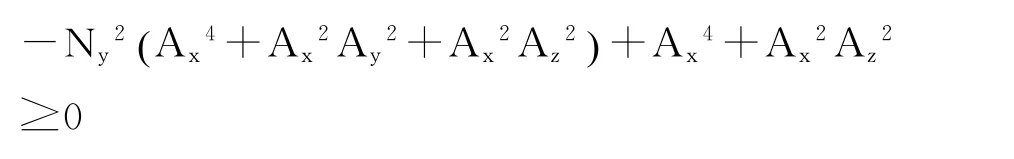
整理得,

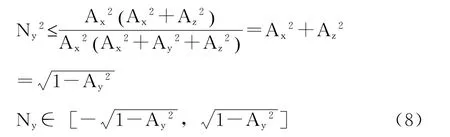
在此范围内随机选取N。

由式(8)得,

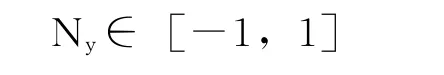
在N和N没有确定的情况下,上述推论结果符合实际情况。同时,N的取值受限于A,也符合实际直观感受。同理其他两个分量,N和N,也有同样的结论。

随机选定N后,由式 (7),N正负取值概率各为50%。这个结果符合直观感受,单位向量A 确定后,N确定后,N 向量只有两种对称的可能情况。再根据式(5),可以唯一确定N。有,

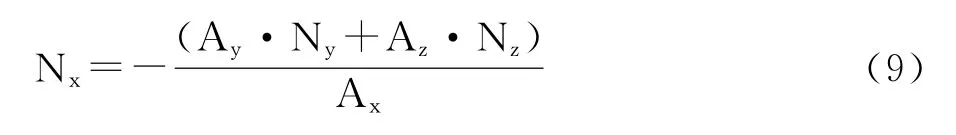
当A=0时,由式(1)有,

同时,由式(5)有,

当A=0 时,那么由式 (1),必有A=±1。由于在随机生成关键姿态向量步骤中,A 向量已经确定了,故无需讨论此时A的取值概率。由式(5),有,

由式(6)有,

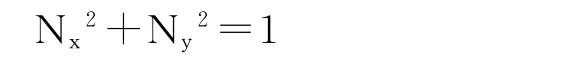
整理得,

通过式(13),在N随机选定后,可确定N。N正负选取概率各为50%。

为保证N有实数解,根号内参数有限制,

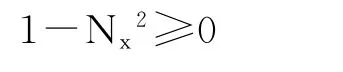
整理得,

在此范围内随机选取N。

对于N 向量,在N和N没有确定的情况下,N的取值范围与上述此推导取值范围一致。

当A≠0时,由式(11)有:

代入式(6),有,

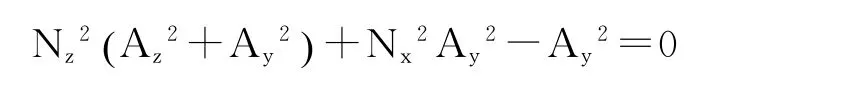
联立式(10),有,

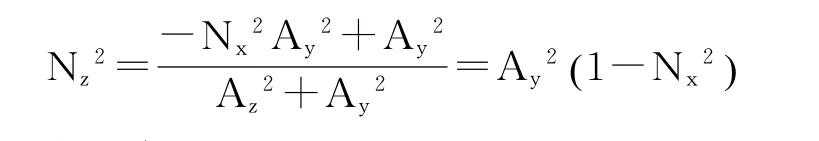
整理得,

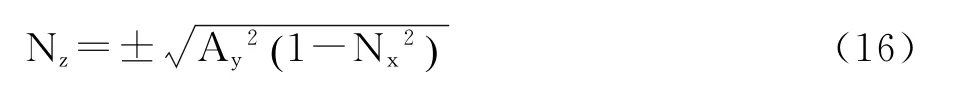
通过式(16),在N随机选定后,可确定N。N正负选取概率各50%。

为保证N有实数解,根号内参数有限制,

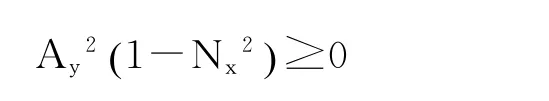
整理得,

在此范围内随机选取N。

同样的,对于向量N,在N和N没有确定的情况下,N的取值范围与上述此推导取值范围一致。

2.4 随机生成姿态向量O

Y 轴的单位向量O 可通过Z轴向量A 和X 轴向量N 获得(右手坐标系),

综上,通过公式 (2)、公式 (3)、公式 (4),可以随机生成向量A。

当A≠0时,根据式 (9)、式 (8)和式 (7),可以随机生成向量N。

当A=0,A=0 时,根据式 (14)、式 (13)和式(12),可以随机生成向量N。

当A=0,A≠0 时,根据式 (17)、式 (15)和式(16),可以随机生成向量N。

根据式(18),可以随机生成向量O。

3 笛卡尔坐标系随机样本程序实现

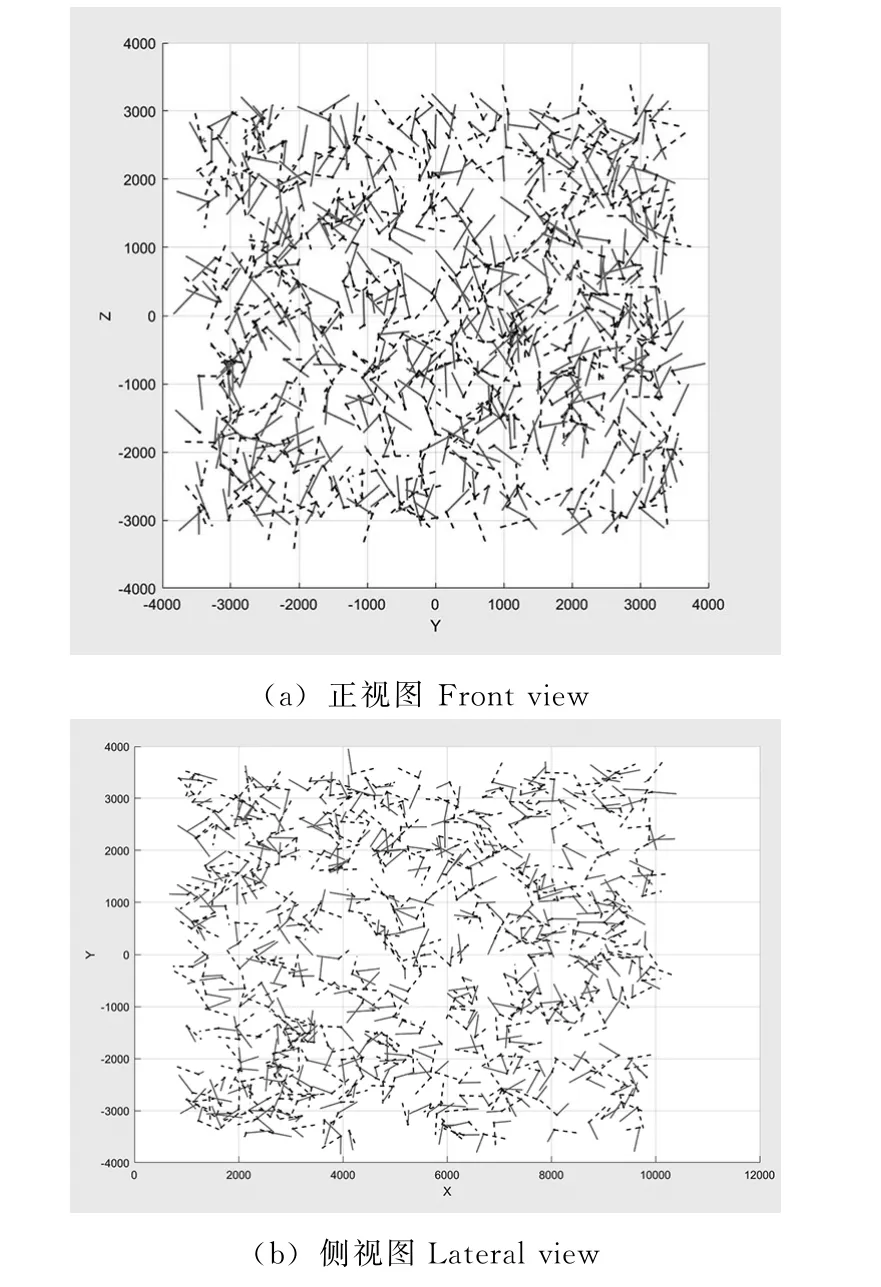
在摄影机器人项目中,随机生成目标位姿的空间为长方体。具体为,在轨道方向1到10米,宽7米,高6米的工作空间内随机生成满足均匀分布的500个目标位姿坐标系。算法采用Matlab软件环境实现,为降低图像显示复杂度,目标位姿显示Z轴(实线)和X 轴(虚线),不显示Y 轴。程序结果如图1所示。

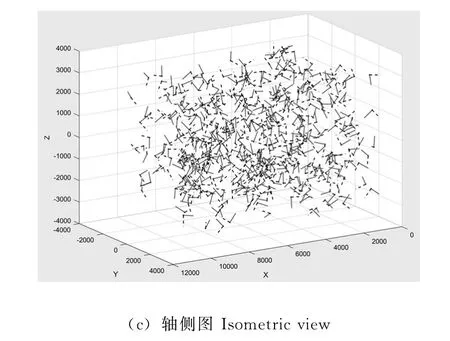
图1 随机生成目标位姿样本

4 结论

为采用蒙特卡洛法描述多轴机器人运动学反解算法性能,首先需要得到工作空间内的目标位姿的随机样本。本文对随机生成笛卡尔坐标系进行了详细的数学分析,通过编写程序获得了摄影机器人工作空间内的目标位姿随机样本。本文的成果可以作为基础元素应用到其他研究中,提高程序编写效率。