基于ABAQUS的制动盘周期结构金属材料变化对制动噪声的影响分析

余亚敏　陆晶晶

摘 要：尽管在汽车行业中盘式制动器的技术较为成熟，但由于制动噪声的复杂性和不确定性，仍需不断改进优化。论文通过多种周期结构的对比，采用了比强度高、比刚度大的金字塔型点阵周期结构金属材料对钳浮式制动器的重要组成部分——制动盘进行了改进设计。其中新型结构包括HT250、合金锻钢、QT600-3以及RuT380四种材料下的三角形截面、圆形截面、正方形带圆角8x8、正方形无圆角8x8以及正方形无圆角10x10四种单胞杆件截面，从而获得实心制动盘和改进制动盘的复特征值的实数部分的数值。建立了模糊综合评价模型，25种改进设计结构中有17种表现出降噪效果，该结果论证了新型周期结构材料的变化在合理的设计下能够达到制动降噪的效果，对新型周期结构制动盘的降噪效果分析和其在航空航天领域以外的汽车领域的应用具有重要意义。关键词：制动盘;金字塔型点阵周期结构;模糊综合评价模型;复特征值;制动噪声中图分类号：U445  文献标识码：B  文章编号：1671-7988（2020）01-134-04

Abstract： Although the technology of disc brake is mature in automobile industry， it still needs to be improved and optimized because of the complexity and uncertainty of braking noise.Through the comparison of various periodic structures， this paper improves the design of the brake disc， which is an important part of the clamp floating brake， by using the metal material of pyramid lattice periodic structure with high specific strength and stiffness. The new structure includes HT250， alloy forged steel， QT600-3 and RuT380 with triangular section， circular section， square with round angle 8x8， square without round angle 8x8 and square without circle. The cross sections of four kinds of single-cell rods with angle 10x10 can obtain the real values of the complex eigenvalues of solid brake disc and improved brake disc.This paper establishes a fuzzy comprehensive evaluation model.Seventeen kinds of structures show noise reduction effect. The results demonstrate that the change of new periodic structural materials can achieve the effect of braking noise reduction under reasonable design. It is of great significance to the analysis of noise reduction effect of new periodic structural brake discs and their application in automobile field outside aerospace field.Keywords： Pyramid Lattice Periodic Structure; Fuzzy Comprehensive Evaluation Model; Complex Eigenvalue; Brake NoiseCLC NO.： U445  Document Code： B  Article ID： 1671-7988（2020）01-134-04

前言

随着互联网公司等造车新势力的加入，使汽车行业的竞争压力逐年提升，与此同时，汽车的普及率也随之提高，方便了人们的日常出行。但它也是一把双刃剑，即使在千人保有量不到两百的中国也存在噪音污染问题，尤其是制动器在连续制动时发出的高频噪音。目前汽车厂商普遍青睐于盘式制动器，也有小部分车型使用鼓式制动器。盘式制动器之所以被广泛使用，是因为它与鼓式制动器相比有以下几个突出的优点：热穩定性能好;浸水后效能降低较少;维修方便等。虽然盘式制动器的技术较为成熟，性能较好，但由于噪声机理的复杂性、出现频段的不确定性、系统性改进方案的缺乏以及汽车消费者的高要求，制动噪声问题有待进一步解决。

1 研究现状

1.1 制动噪声研究现状

早期研究者通常从自激振动的角度进行制动噪声的研究，很自然地从摩擦副入手，Millner[1]证明了对于盘式制动器即使摩擦系数为常数，制动噪声仍可发生。Sprag-Slip理论[2]解释了当摩擦系数为常数时，仅因摩擦副的几何特性选择不当，便会导致系统自激振动的产生。Hany A.Sherif[3]认为自激振动依赖于两滑移面的接触特性——接触面的摩擦系数和接触刚度。另一个解释制动振动噪声机理的分支是热点理论，Kreitlow通过试验发现颤抖频率与车辆速度和热点数目相关。

刘宇澄[4]围绕制动衬块结构优化，引入了压缩应变作为调整变量，解决了不同结构参数之间缺乏统一参照的问题，实现了调整衬块轮廓、修改衬块宽度以及在衬块两端开设倒角三种技术手段在降噪效果方面的对比。

曾康等[5]使用MOPA激光器在制动盘表面加工出4种不同数量及深度的M型沟槽并在LINK3900台架实验设备上进行NVH台架实验，对比分析不同空旷下M型沟槽对制动噪声的影响。

1.2 新型周期结构材料研究现状

声学超材料是人工周期复合材料，因其所具备的超常特性，近年来受到国内外学者的广泛关注。FokL[6]等人在其综述性文章中明确指出，目前声学超材料的两大突出应用方向为：高效降噪材料和高性能声学透镜。其中，在降噪应用探索方面，最近香港科技大学研究小组取得了重要进展。2010年，他们设计、制备出一种轻质薄膜构型的局域共振型声学超材料，可以在低频宽带（50Hz～1000Hz）范围内实现高效隔声。

三聚氰胺泡沫材料是一种具有高开孔率的多孔材料，具备优良的吸音、防火隔热及环保性能，可以作为吸声材料与弹性板、空腔介质形成复合结构，在建筑、航空、交通工具等工程领域有广泛的应用。白聪[7]等详细分析了多孔材料布局对复合结构吸声特性的影响。他们研究的结果表明：在多孔材料前面增加空气层可以改善高频吸声特性;在多孔材料后面增加空气层可以改善复合结构低频吸声特性。虽然该复合结构对高频吸声有效，但是建模时有一定的难度。

点阵材料[8]是一种新型的胞状有序多孔材料，其单胞为杆单元组成的空间网架类结构。金属基点阵材料具有良好的力学性能和功能特性，在航空航天、交通运输、武器装备、电子器件等领域有着广泛的应用前景。陈婷婷[9]等人基于直接声振耦合理论，用数值分析较为系统地研究了金字塔型空心点阵地隔声特性并分析了空心杆件的仰俯角、面内尺寸等重要结构参数对金字塔型空心点阵结构隔声特性的影响。

点阵结构因其比强度高、比刚度大等优良力学性能被广泛用作航天器、汽车等的外壳结构。由于点阵结构所处的部位和工况环境经常承受声压载荷激励，故研究其隔声特性具有重要意义，在航空航天、高速列车、汽车、船舶、潜艇等领域具有十分广阔的应用前景。

2 周期结构设计

在实际情况中，金字塔点阵结构内充满着空气，声波可以通过空气腔和声桥连接结构两种媒介传播。CHENG[10]等研究表明：当声桥连接结构刚度与空气腔的空气静力刚度之比大于10时，可以不考虑声波经过空气传播的途径而忽略空气腔与结构面板之间的流固耦合作用。本文研究的模型符合上述条件，所以计算时均忽略金字塔型点阵结构中空气的影响。

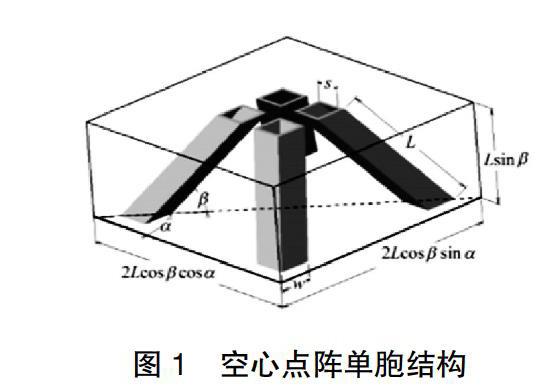
陈婷婷等建立了金字塔型空心点阵结构单胞结构（图1）并进行隔声量的对比分析，文中指出空心点阵结构有利于轻量化且隔声性能相对较好，所以我从一开始建模就从空心点阵结构入手，但由于跟我同一小组做强度分析的同学因空心结构的壁过薄无法对其进行网格划分，所以我的单胞结构确定为实心点阵结构。

金字塔型点阵单胞结构的主要参数有杆件长度L，杆件与面板的方位角α，仰俯角β，杆件截面为正方形的实心杆件边长或杆件截面为正方形管的空心杆件外壁边长为w，内壁边长为s。

3 有限元模型及振动模态特性分析

3.1 有限元模型

将有限元法把离散的概念运用到整个连续物体从而使整体解析变成分段解析，将解析法与数值法完美结合，形成一种全新的数值计算方法。有限元分析法的核心内容是“分与合”，分是为了获得有限个单元，从而对单元进行分析，合是为了集合划分的单元，对整个物体进行综合分析。完成网格划分的模型如图2所示。整个盘式制动器模型被划分为56477个单元，节点总数为100593。

3.2 制动盘模态分析

模态分析是结构设计中的常规方法。因为制动器也是一个振动系统，在其结构的设计和优化中引入模态分析，有利于结果的分析。

模态分析[11]可以用来确定结构的自振频率和相应振型，避免在动载荷作用下发生共振现象，从而提高系统的振动性能。本文利用有限元分析软件ABAQUS，对改进制动盘有限元模型进行模态分析，发现制动器制动过程中发生共振的原因，为制动器的结构优化提供重要的模态参数。制动过程主要是把制动力加载到制动器的对偶盘上，运动中的摩擦片受到对偶盘挤压产生摩擦力，从而实现车辆的制动减速。随着摩擦的增加，两种相邻的模态会相互融合起来。当其达到相同频率时，就会出现其中一个不稳定的现象。由于特征值的实部值与不稳定模态直接相对应，可以提取复合特征值，从而确定其中的不稳定模态。当一个有限元运动学系统有n个节点自由度时，就会有n个特征矢量和特征值与其对应。而每个特征值又与系统某阶的固有频率相对应，相应的特征矢量同样与固有频率下的振型相对应。当实部特征值大于零时，系统就会运动不稳定。在微小的干扰下，系統的振幅会越来越大，随即就会产生摩擦噪声。

4 评价模型

由于散点图只能通过大概地比较得出结论，无法将25种改进结构都进行详细地描述，所以需要建立评价模型使得改进制动盘的降噪效果的好坏更加直观。

4.1 根据评价目的确定评价指标集合

当评价指标集合为={实部值的最大值，频率为1～16kHz的个数，频率在1～16kHz且实部值小于380的个数，频率在1～16kHz且实部值大于380的个数}

之所以将频率选择在1～16kHz之间是因为本设计主要研究高频噪声且该频段内的噪声往往是由于制动盘所引起。实部值的最大值出现的原因是制动盘的共振现象，所以该指标尤为重要。

4.2 根据评价目的确定评价指标集合

评价等级[12]集合为={很好，好，一般，差}

评价等级一般分为四等，但是由于评价等级受到个人感受的影响，有的评价模型种的评价就采用几个专家的评价。

4.3 确定各评价指标的权重

评价指标权重为={0.4，0.2，0.2，0.2}

4.4 确定评价基准

以HT250实心制动盘的数值作为评价基准，由于频率在1～16kHz的个数无法准确表达实部值的大小，所以添加了另外两个指标，即频率在1～16kHz且实部值小于380的个数和频率在1～16kHz且实部值大于380的个数。380这个数据为HT250实心制动盘的实部值最大值的一半，这样选择是因为380将作为评价基准的制动盘数据分为两大类，既考虑频率的范围又考虑了实部值的数值同时又不至于设置过多的指标。评价结果：

式（1）中，a0是HT250实心制动盘实部值的最大值;a是改进制动盘实部值的最大值;b0是HT250实心制动盘频率在1～16kHz的个数;b是改进制动盘频率在1～16kHz的个数;c0是HT250实心制动盘频率在1～16kHz且实部值小于380的个数;c是改进制动盘频率在1～16kHz且实部值小于380的个数;d0是HT250实心制动盘频率在1～16kHz且实部值大于380的个数;d是改进制动盘频率在1～16kHz且实部值大于380的个数。得到最终评价结果，如表2所示。

5 结论

25种改进结构中有19种表现出良好的降噪效果，其中降噪效果最好的是三角形截面合金锻钢制动盘，与上一章通过数据分析的结论相一致，进而证明了该评价模型具有一定的可靠性。

参考文献

[1] Millner N.A theory of drum brake squeal[J].I Mech E，1976，c39/76： 170-185.

[2] Spurr R T.Brake squeal[J].I Mech E，1971，95/71：13-15.

[3] Hany A Sherif， “On the design og Anti-Squeal Friction Pads for Disc Brake”，SAE paper 910575.

[4] 刘宇澄.乘用车盘式制动器制动嗓声影响因素分析及参数优化方法研究[D].浙江大学，2017.

[5] 曾康，张雪刚，王书文.M型沟槽仿生制动盘的减振降噪性能研究[J].噪声与振动控制，2018，38（S1）：292-295.[1]唐宗贤，朱赋主编.高等数学：上册.第2版.北京：机械工业出版社，1996.

[6] FokL， AmbatiM， ZhangX. Acousticmetamaterials[J]. MRSBuletin. 2008，33.

[7] 白聪，沈敏.含三聚氰胺多孔材料分层复合介质吸声特性[J].应用声学，2019，38（01）：76-84.

[8] 黄英杰. 三维Al基点阵材料设计、制备及力学性能研究[D].中国科学技术大学，2017.

[9] 陈婷婷，刘杰，谭栋国，文桂林.金字塔型空心点阵结构的隔声特性研究[J].振动与冲击，2017，36（23）：209-215+231.

[10] CHENG L， LI Y Y，GAO J X，et al.Energy transmission in a mechani -callylinked double-wall structure coupled to an acoustic enclosure [J].Journal of the Acoustical Society of America，2005， 117（5）： 27422751.

[11] 趙敬.基于CAD/CAE技术的盘式制动器结构优化问题研究[D].河北工业大学，2007.

[12] 周佺.基于熵权模糊综合的水资源考核评价方法研究与应用[J].地下水，2019，41（02）：112-115.