网络画板应用之椭圆轨迹的常用作法

文/中山市实验中学

网络画板(http://www.netpad.net.cn/)是一款支持在互联网、移动互联网环境下运行的专业的数学学科工具软件,是开放共享的移动数学实验室，可以让数学更有趣，更直观.基于此，笔者应用网络画板的工具，列举一些高中阶段椭圆轨迹的常见作法，并给出具体的作法步骤和设计思路.

一、利用椭圆的定义作图(图一)

定义：我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.

作法：(1)作圆F1,并在圆内任取一点F2.

(2)在圆上任取一动点M，连接MF2并做其中垂线l，中垂线l与MF1交于点P.

(3)依次选中M和P点，选择轨迹.

设计思路：作MF2的中垂线l，使得PF2=PM，从而|PF1|+|PF2|=|MF1|(恒等于大圆半径)，而且F2在圆内，所以|F1F2|<|MF1|符合椭圆的定义.如果把点F2拖到圆外，轨迹则是双曲线.

二、已知圆A:(x+a)2+y2=r2,圆A内有一定点B(a,0),圆P过点B且与圆A内切，作圆心P的轨迹(图二)

作法：(1) 在x轴上找两个关于原点的对称点F1,F2，并作大圆F1，并在大圆上找一个动点M.

(2)连接MF1和MF2，作MF2的中垂线l，交MF1于点P.

训导他们的人是老崔，老崔是物业经理，这些日子，停车事件频频发生，有涵养的老崔嘴上起泡，心里长毛，天天在小区里东转西转，眼睛东瞄西扫，恨不得到哪里发现一块新大陆。他的副手还带着保安在背后嘲笑他，说，这个小区有什么转头的，老崔这是找车位呢，还是找老鼠洞？

(3) 以P为圆心MP为半径作圆.

(4) 依次选中M和P点，选择轨迹.

设计思路：类似于图一的作法,根据椭圆的定义找到P点位置.因为PM=PF2,所以以P为圆心，PM为半径作圆P满足题意.

图一

图二

三、在圆x2+y2=a2上任取一点P，过P点作x轴的垂线段PD，D为垂足，当P在圆上运动时，作出线段PD的中点M的轨迹(图三)

作法：(1) 作圆O，并在圆上取一动点M.

(2) 作x轴的垂线MD，垂足为D,并取MD中点P.

(3) 依次选中M和P点，选择轨迹.

四、设点A，B的坐标分别是(-a,0)，(a,0).直线AM，BM相交于点M，且它们的斜率之积是定值b(b<0,b≠-1)，作出点M的轨迹(图四)

作法：(1)在x轴上取两个关于原点的对称点A，B.

(2)新建一个变量b(b<0,b≠-1)为斜率之积.

(3)以A为圆心做小圆，并在圆上任取一点M，过A,M点作直线l.

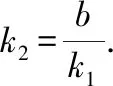
(5)计算测量出B点的横坐标xb，作出直线y=k2(x-xb)并交l于点P.

(6)依次选中M和P点，选择轨迹.

设计思路：这是人教版选修2-1中P41例3的一般情况，其实当-10时表示双曲线.

图三

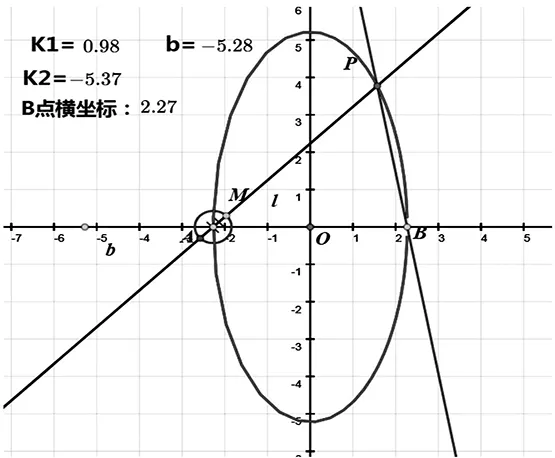
图四