基于多智能体强化学习的多AGV路径规划方法

刘 辉，肖 克，王京擘

（青岛大学 自动化系，青岛266071）

AGV路径规划是指为每个AGV 规划一条从起始地址到目标地址的无碰撞最优路径[1-2]。AGV路径规划方法有运筹学模型优化方法、A*算法[3]及其各种变体和各种智能优化方法，如遗传算法[4]，蚁群算法[5]，粒子群算法[6]等，强化学习通过奖赏与惩罚来优化马尔科夫决策过程中的智能体的策略，它不依赖环境模型和先验知识，逐渐成为机器人在路径规划的研究热点[7-8]，强化学习也被尝试用于解决多智能体协作问题，如多路口交通信号灯协调控制问题[9]等。常见的多智能体强化学习有EMA Q-learning[10]、WoLF-PHC[11]、Nash Q-Learning[12]等，另外强化学习也被用来和其他算法结合解决路径规划问题，文献[13]将多智能体环境虚拟为人工势能场，通过先验知识获取相应的势能值，再利用分层强化学习进行更新策略，文献[14]在强化学习的基础上使用神经网络来估计Q值，用以解决移动机器人的避障问题。

针对传统多智能体强化学习在路径规划时容易陷入维数灾难和局部最优等问题，本文根据传统的Q-learning 提出一种多智能体独立强化学习MRF Q-learning算法，智能体不需要知道其他智能体动作，减小了动作空间，将Boltzmann 策略与ε-greedy策略结合，更好地协调探索与利用，通过获得全局最大累积回报的频率更新Q值公式，以获得全局最大累积回报。

1 路径规划框架

1.1 环境建模

路径规划常用的建模方法有栅格法、可视图法和拓扑地图法等，本文采用栅格法对AGV 工作环境进行离散化处理，如图1所示。

图1 AGV 运输任务环境Fig.1 Environment for AGV’s transport missions

在货物运输多AGV 环境中，AGV 之间需要通过协调合作以最短的时间完成任务，地图中的栅格通过坐标来表示，根据AGV和工作站等坐标位置来描述它们之间的联系，整个环境被分为两类工作区，分别为智能体的独自运输区（运输区域1、运输区域2）和公共运输区，图中圆形图标代表AGV，方形图标代表工作站，工作站在地图中随机分布，但每个区域仅有2个工作站。

1.2 任务分配

单AGV路径规划任务中的AGV 仅需要最大化自己的利益，而本文主要研究多智能体之间合作任务，完成运送任务的路径规划问题，需要智能体最大化整体利益，我们设置除了公共运输区两个AGV 都可进入外，AGV1和AGV2分别只能在运输区域1和运输区域2内移动，我们并不指定每个AGV运输货物所经过的工作站数量，任务的目标为协调优化两个AGV 在各自运输区和公共运输区运送货物的行驶轨迹，要在避免碰撞的情况下，使用最少的时间步长将足量的货物运送至所有的工作站。

1.3 路径规划算法

静态路径规划问题中，对全局信息已经掌握，单AGV路径规划时不会受到其他AGV的影响，能够较好地找到理论的最优路径，但对于多AGV路径规划，多个AGV 之间相互影响，难以获取整个全局信息，另外，由于需要多智能体相互配合完成任务，对于常见的一些路径规划算法难以处理智能体之间联系，获得时间最优路径，因此本文提出一种多智能体强化学习MRF Q-learning 方法来解决多AGV 合作路径规划问题，目标为获得全局最大累积回报，从而以最短的时间步长完成任务。

2 多智能体强化学习路径规划算法

2.1 Q 学习

Q-learning（Q 学习）是一种经典的强化学习算法，它将智能体在每个状态下采取的动作的Q值用Q_table 进行存储，通过不断迭代更新，逼近目标函数Q*，而且不需要环境的先验知识，是一种modelfree（无模型）算法，其Q值更新公式如下：

式中：r为状态s 下选择动作a时获得的立即回报；A为智能体的动作集；α为学习率，表示Q值更新的程度；γ是折扣因子，γ越小则越注重当前的回报。由于Q-learning为单智能强化学习方法，而多AGV路径规划为多智能体环境并且需要AGV相互合作，因此我们在其基础上，设计出一种能够解决合作问题的多智能体强化学习方法。

2.2 多智能体强化学习

多智能体强化学习模型在元素组成上与单智能体强化学习类似，包含智能体、环境状态、动作、回报，模型如图2所示，多个智能体之间相互作用与环境进行交互，根据获取的状态和回报来学习改善自己的策略。

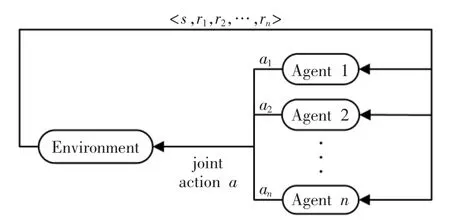
图2 多智能体强化学习模型Fig.2 Multi-agent reinforcement learning model

2.3 MRF Q-learning路径规划算法设计

2.3.1 状态空间和动作空间设计

多智能体系统中状态转变受到其他智能体影响，另外本任务需要AGV 将货物送至多个工作站，所以环境状态的定义与AGV是否经历过工作站息息相关，因此我们根据每个智能体的位置，工作站是否收到货物来定义系统的状态，状态定义为

式中：si为AGVi的位置；vj为工作站j的收到货物的状态；vj∈｛0，1｝，0代表未收到货物，1代表已收到货物，此时状态空间大小为10000×2j。

在多智能体合作任务中，由于AGV 之间需要进行交互，因此许多多智能体强化学习算法需要智能体之间分享动作信息来更新策略，因此联合动作集为A=A1×A2，…，×An，其中Ai为智能体i的可行动作集，此时每个智能体都需要小的空间存储Q值，随着智能体数的增多，占用的空间会以指数级增长，因此本文采用一种独立强化学习方法解决联合维数灾问题，每个智能体只需要使用自己的动作和其他信息来更新策略，因此Q值存储空间减小为在本任务中每个AGV的动作集都为包含上、下、左、右4个动作。

2.3.2 奖励函数

奖励函数代表了智能体所选择的策略的价值，因此智能体是根据奖励函数的指导来完成任务的。奖励函数设计的优劣会直接影响学习到的策略的好坏，常用的设置奖励函数的方法有稀疏奖励、分布奖励、形式化奖励等，本文使用的为稀疏奖励函数，如式（3）所示：

式中：r1，r2，r3，r4>0，在路径规划任务中，由于AGV之间有着部分相同的工作领域，因此可能会发生碰撞以及出界的情况，为了避免AGV 发生碰撞或者出界，我们设置当发生以上2种情况时，AGV 会获得一定的惩罚，即负的回报，当智能体完成目标时会给智能体较多的奖励，以确保智能体能够完成任务，另外，为了使智能体学到完成任务的最短时间步长，我们设置AGV每次采取行动都会获得一定的负的回报，因此AGV 会学习以较快的速度完成任务。

2.3.3 动作选择策略

强化学习算法常常面临探索与利用的问题，探索是尝试不同的动作以获得一些更好的策略，利用则是采取当前状态下的最优策略，探索更加注重于长期利益，而利用则是对短期利益的最大化，因此需要平衡两者之间的关系，常用的探索与利用策略有ε-greedy 策略、Boltzmann 策略、ucb 策略等。

由于多AGV路径规划受到多个智能体的影响，容易陷入局部最优的情况，为了避免错过一些短期表现一般而有着较好的长期表现的动作，本文将ε-greedy 探索策略与Boltzmann 策略结合，具体决策方法如下所示：

式中：αi为智能体i 选择的动作；ε∈[0，1]为探索率，设置以ε的概率选择随机选择一个动作，以1-ε的概率根据Boltzmann 探索策略进行动作选择，Boltzmann 动作选择的概率如下所示：

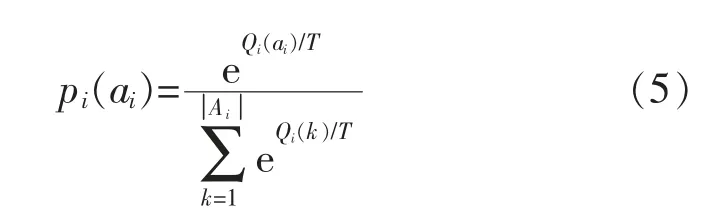
式中：pi（ai）为智能体i 选择动作ai的概率；Qi（ai）为智能体i 选择动作ai的Q值；∣Ai∣为智能体i的动作集。

2.3.4 最大回报频率价值更新函数

由于多AGV路径规划问题为多状态优化任务，目标为最大化全局累积回报，我们据此设计了一种全局最大累积回报频率强化学习方法来解决路径规划问题，首先，每个智能体分享其回报，智能体i 获得的立即回报为ri，则全局立即回报为

在每个episode 都记录每个时刻的立即回报、选择的动作、状态等，每个状态被经历到达一定次数后，在每个episode 结束后根据每个状态s 下的全局累积回报R 获取全局最大累积回报Rmax，全局折扣累积回报定义如下：

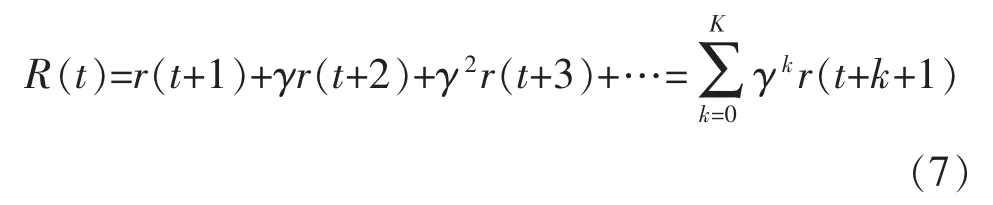
式中：γ为折扣因子，γ越小则越注重当前的回报；K代表一个episode所用的时间；r（t+1）代表在t+1时刻的全局立即回报，由式（6）获得，根据全局最大累积回报Rmax更新最大累积回报获取的频率，获得全局最大累积回报的频率公式如下：

式中：nai为智能体i 在状态s 选择动作ai的次数；nmax_ai为智能体i 在状态s 选择动作ai获得全局最大累积回报的次数。根据频率f（s，ai）更新Q值，如下：

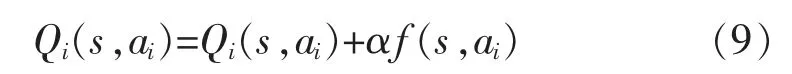
通过引入全局最大累积回报频率更新Q值，能使得智能体能最大化整体的利益，找到完成任务整体耗时最短路径。

算法步骤如下所示：

步骤1定义所有AGV的立即回报之和为全局立即回报

步骤2初始化每个AGV的Q值、动作选择次数、全局最大累积回报及获取次数等变量；

步骤3根据式（4）Boltzmann与ε-greedy 结合策略进行动作选择；

步骤4记录每个时间步长的动作、状态、立即回报等变量；

步骤5每种状态被经历一定次数后，在每个episode 结束后，根据记录获取每个状态s 下的全局最大累积回报Rmax；

步骤6统计AGV 选择动作ai时获得历史全局最大累积回报的次数，根据式（8）更新获得全局最大累积回报的频率f；

步骤7根据式（9）更新Q值函数；

步骤8若到达预先设置的学习次数，进入步骤9，否则继续执行步骤3；

步骤9每个AGV 选择具有最大Q值的动作。

2.4 MRF Q-learning算法重复博弈验证

为了验证MRF Q-learning算法的性能，我们设置了2种最优纳什均衡（具有全局最大立即回报的纳什均衡点）不同分布的两人两动作重复博弈，最优纳什均衡点用括号标记，如图3所示，由于重复博弈为只含有一个状态，因此在重复博弈中，MRF Q-learning算法中相关的全局最大累积回报为全局最大立即回报。

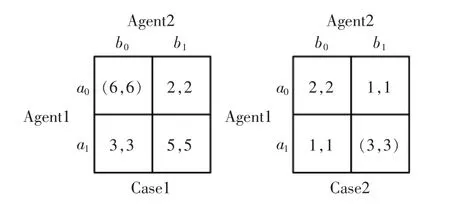
图3 重复博弈支付矩阵Fig.3 Repeated game payoff matrices

我们设置12 组不同的初始概率及Q值（初始概率如图4和图5中圆点所示）每次实验运行了20000步，最终结果如图4和图5所示，图中pa0代表智能体1 选择动作a0的概率，pb0代表智能体2 选择动作b0概率，可以看出MRF Q-learning算法在两种情况的重复博弈中都收敛到了最优纳什均衡。

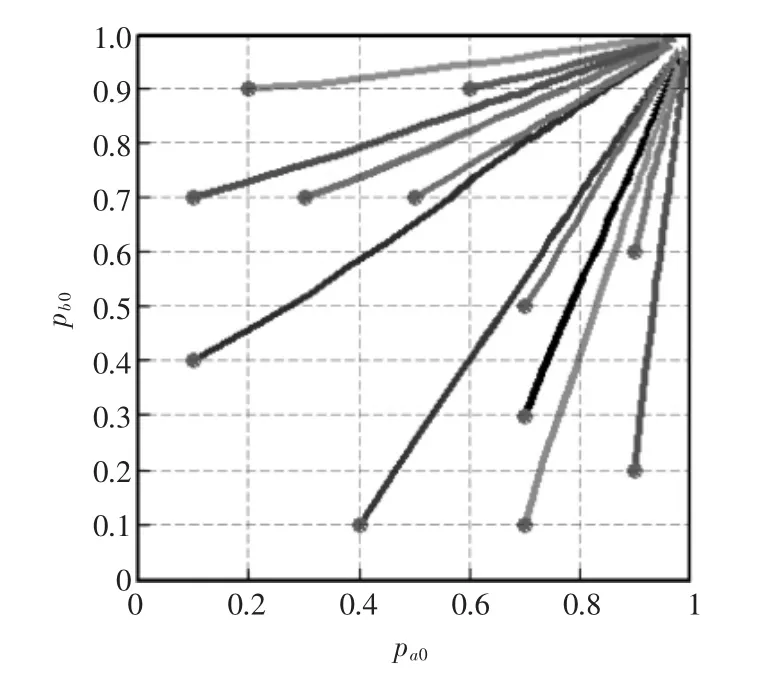
图4 Case 1 动作选择概率Fig.4 Probability of choosing action in Case 1

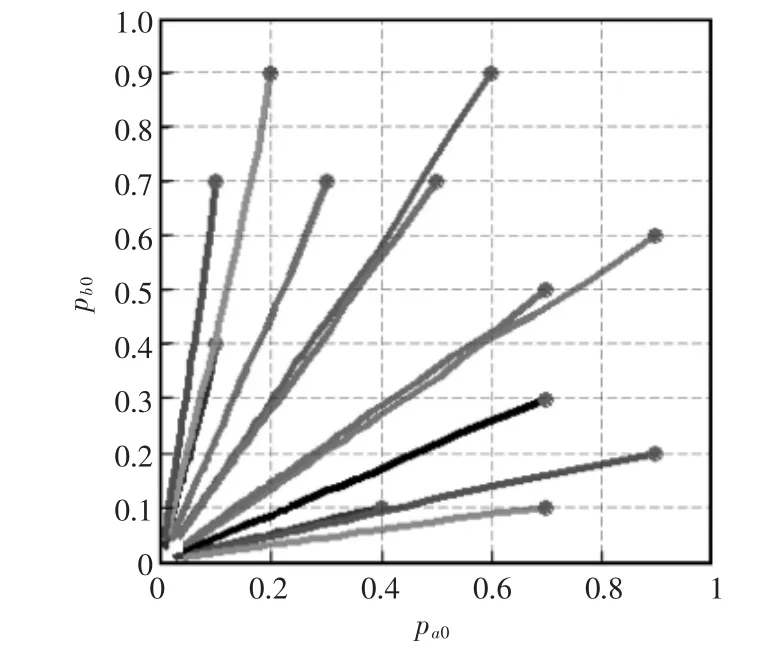
图5 Case 2 动作选择概率Fig.5 Probability of choosing action in Case 2

3 实验仿真与分析

3.1 实验设置

为了验证MRF Q-learning算法解决路径规划问题的有效性，通过路径规划仿真进行测试，并与多智能体强化学习算法EMA Q-learning 进行对比。两种地图环境如图6和图7所示，具体任务在第一节中做出了详细介绍，另外，我们设置当AGV 行动超过500个单位时间步长时任务结束，任务完成或结束记为一个episode，若两个AGV 发生碰撞或出界，则它们保持上一时刻的位置，每种环境下我们都运行了20000 episodes，我们对此任务的具体的奖励函数做如下设置：

并设置学习率α=0.4，折扣因子γ=0.9，在episode 开始时需要对动作进行大量探索，设置探索率ε为一个较大的值，然后逐渐减小，T=1 并随着episode 不断衰减，探索率设置如下：式中：n为当前episode 数；M为最大episode 数

3.2 实验结果分析

我们根据程序运行结果，评价阶段最终路线如图6和图7所示，图中实线表示MRF Q-learning的最终路径，虚线表示EMA Q-learning的最终路径。

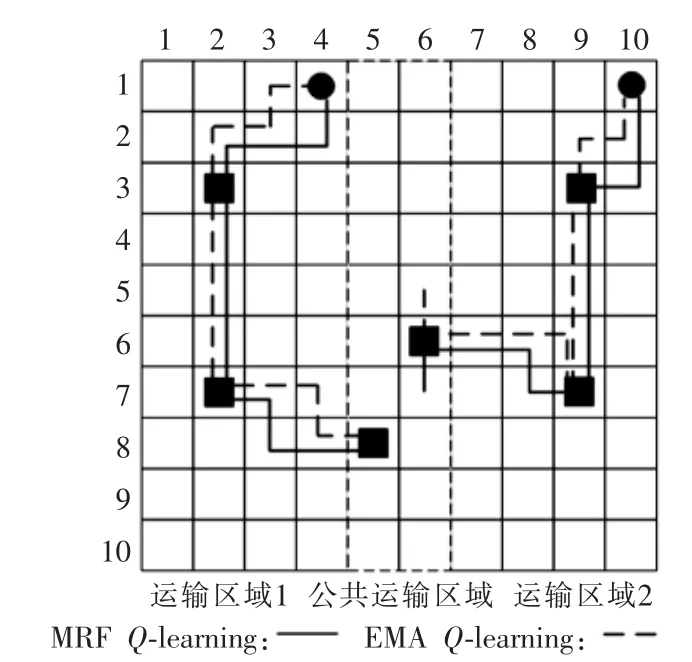
图6 环境1 实验结果示意图Fig.6 Experimental results diagram in environment 1

图7 环境2 实验结果示意图Fig.7 Experimental results diagram in environment 2

两种环境中每种算法在评价阶段的时间步长与最优时间步长如图8所示。

图8 评价阶段的时间步长Fig.8 Time steps in the evaluation phase

可以看出本文的MRF Q-learning 在两种环境中都找到了时间步长最短路径，而EMA Q-learning虽然在第一种环境中也以最短的时间步长完成了任务，但在环境2 中两个AGV 之间没能相互配合，左边的AGV1 经过了4个工作站，而AGV2 仅经过2个工作站，延长了运输时间，且在两处产生了出界的情形，虽然也完成了运送任务，但没能找到时间最短路径。

图9为两种算法在环境2 中学习阶段的平均步长，可以看出EMA Q-learning 一开始学习速度较快，MRF Q-learning 由 于 将Boltzmann与ε-greedy结合，学习过程中会较多地探索其他动作，因此前期学习速度相对较慢。两种算法在最后都收敛到了较短路径，但MRF Q-learning最终收敛到了比EMA Q-learning时间步长更短的路径。

图9 学习阶段的平均时间步长Fig.9 Average time steps in the learning phase

4 结语

本文针对工作站货物运输多AGV的路径规划问题，提出一种多智能体强化学习MRF Q-learning算法，算法采用全局最大累积回报频率进行更新Q值公式，以获得全局最大累积回报，每个智能体不需要其他智能体的动作，避免了联合动作维数灾，将Boltzmann 策略与ε-greedy 策略结合，更好地协调探索与利用，多AGV路径规划仿真结果说明，与其他多智能体强化学习算法相比，本文提出的MRF Qlearning算法能够找到最优路径使总运输时间最短。