基于新型卡尔曼滤波算法的称重系统实现研究

文常保，戚一娉，宿建斌，巨永锋

（长安大学 电子与控制工程学院 微纳电子研究所，西安710064）

称重系统作为测量物体质量的重要工具，被广泛应用于各个行业，其中制药、配料和贵金属等行业对称重系统的精度有较高要求[1-2]。

在称重过程中，信号不可避免会受到干扰，势必影响测量精度，干扰主要有内部干扰和外部干扰，外部干扰指外界的干扰波和环境因素如电磁干扰、静电干扰[3-5]；内部干扰，存在于传感器采集信号和信号数模转换的过程中，以脉冲干扰的方式对信号造成误差[6]，还存在于所有电子器件和传输介质中，以电子热振动导致的温度变化所引起的热噪声[7-8]，热噪声在工作频率范围内的频谱均匀分布，且由内部大量自由电子运动产生，因此属于高斯白噪声，由此，针对内部干扰，提高称重信号的精度具有重要意义。

在内部干扰问题上，从软件算法上进行改进，不仅简化电路，还可以降低硬件的二次干扰和成本，在单一的滤波算法中，对比小波变换、神经网络和模糊理论等算法，卡尔曼滤波在滤除高斯白噪声方面更具有针对性[9-10]。故在此提出基于新型卡尔曼滤波算法的称重系统实现方案，在处理不稳定或者噪声大的被测信号时，改善滤波结果稳定性差而且检测精度低的情况，还可以预测、校正信号中的误差，从而提高称重信号的精度[11]。

1 称重系统结构及算法设计

基于新型卡尔曼滤波算法的称重系统由称重传感器、A/D转换模块、微处理器、存储模块、显示模块以及红外模块等外围电路组成，称重系统结构及算法流程如图1所示。

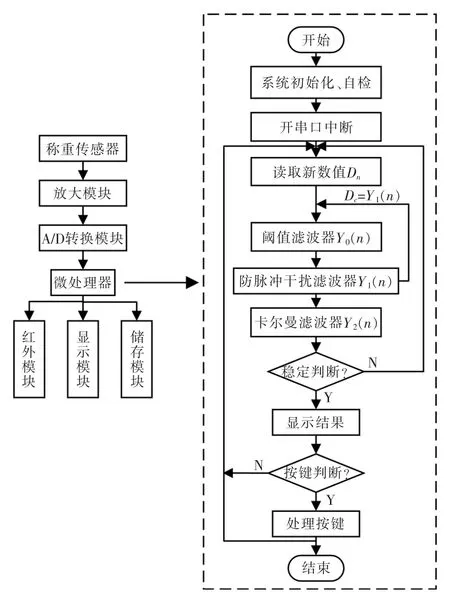
图1 称重系统结构及算法流程Fig.1 Weighing system structure and algorithm flow chart

对待测物进行测量时，称重传感器会将物体的质量转换成电信号，在转换过程中很可能会因脉冲形式的电磁干扰引起误差，由于传感器输出信号在mA级别，所以需要放大模块将电信号放大到A/D转换模块的量程范围内，在这过程中放大模块也会将在称重过程中信号携带的脉冲干扰进行放大，另外，在A/D转换模块将带有干扰的模拟信号转换为数字信号过程中，会因为温度导致热噪声影响其分辨率，进而影响称重系统的精确度，因此，需要对采集信号进行软件滤波，去除干扰和噪声对系统的影响进而提高称重前端测量信号的精度。

对于信号中的高斯白噪声干扰，可以采用卡尔曼滤波算法通过动态调整权值进行滤除，使测量结果无限收敛于真值，但是，传统卡尔曼滤波算法在处理非周期性较大噪声信号时会不可避免的引入线性误差，甚至会导致测量结果较大波动和偏离。

在图1所示基于新型卡尔曼滤波算法的称重系统中，采用阈值滤波方式滤除因偶然因素引起的脉冲干扰，将读取的采样新值D1与系统所允许的最大偏差值进行比较，未超出最大偏差值的会被作为有效采样值，超出则被舍弃使用，并且重新取值，最大偏差值的大小设置标准一般根据系统控制信号的要求范围所选取，如果设最大偏差值为A0，则经过阈值算法的第1次输出值Y0（1）为

式中：D1为第1次的采样值。

循环采样取值时，使用更新的采样值与对比值之差来与系统所允许的最大偏差值进行对比，选取经过防脉冲干扰滤波器得到的平均值Dc作为对比值，若新采样值与对比值的绝对值之差≤A0，则本次采样值Dn有效；若两者之差>A0，则认为发生了较大的随机干扰，本次采样值Dn无效，并选择用对比值Dc来代替本次采样值，因此，可以得到经过阈值算法处理后的第n次（n≠1）输出值Y0（n）为

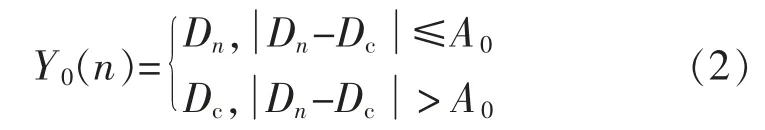
式中：Dn为第n次的采样值；Dc为经过防脉冲干扰滤波器的平均值来更新阈值滤波中的对比值。

由于单独使用阈值滤波算法，在滤除周期性干扰上效果较差，并且存在信号平滑度差等问题，因此可以采用防脉冲干扰滤波消除周期性干扰引起的采样值偏差。

将经过阈值滤波处理后的数据送入防脉冲干扰滤波器，将会得到一组新的队列，在该组队列长度选取上，为保证平均值的可靠性和系统的运行速度，将其设置为以12个采样值为一队列，对新的队列进行连续采样，将新的采样值放在队尾，与此同时将队首的一个采样值剔除，以保持队列的长度不变，接着剔除队列中的最大值和最小值，最终队列长度为10个采样值，对其进行算数平均运算，将运算结果送入下一阶滤波器中进行滤波，且不断更新阈值滤波器中的对比值Dc，以使阈值滤波器能获得更好的滤波效果，经过防脉冲干扰滤波算法的第n次输出Y1（n）为

式中：Y0（n-i）为经过阈值滤波后的第n-i次采样值；M（Y0），m（Y0）分别为12个采样值队列中的最大值、最小值。

经过防脉冲干扰滤波算法后得到平均值，用其更新阈值滤波器中的对比值为

为确保更好地消除噪声，需要构造符合称重系统的状态模型，将上一阶滤波器滤波后的数据作为下一阶滤波器的初始数据值，得到作为估计状态的输入信号值为

在称重状态变化过程中，会使噪声产生波动情况，此时用线性随机微分方程描述信号值，当信号经过防脉冲干扰滤波算法后，信号值在n时刻的值是n-1时刻的值加上控制信号和过程噪声的线性组合，经过滤波后的信号值可用线性随机微分方程描述为

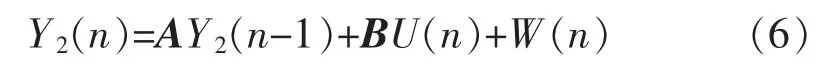
式中：Y2（n-1）分别为预估计n-1时刻状态变量的值；U（n）为对系统的控制信号，因系统中没有控制信号影响，故可将其略去；W（n）为符合高斯分布的过程激励噪声；A和B为系统参数矩阵。

在经过滤波后的信号值转变为测量值的过程中，存在传感器测量到符合高斯分布的噪声，即测量噪声，测量值用线性随机微分方程描述为

当构造完模型后，开始进行迭代估算，其具体过程可以分为时间更新和测量更新2部分，时间更新部分得出的值为先验值，测量更新部分得到的值为后验值。

在时间更新部分，对n时刻的先验状态估计值Y2（）粗略估计为

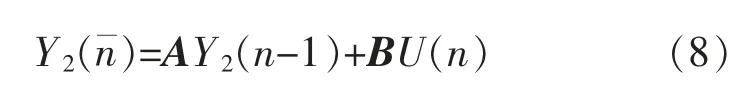
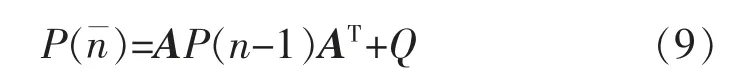
式中：P（n-1）为n-1时刻后验估计误差协方差；Q为过程噪声W（n）的协方差。

进入测量更新部分后，先根据预测的误差协方差P（n）和测量噪声信号V（n）的协方差R 来计算得到增益，即

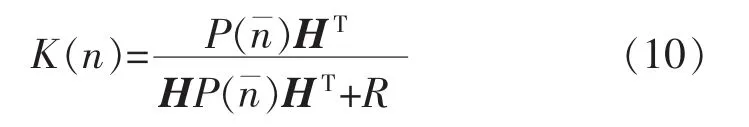
用得到的增益K（n）来计算状态n时刻的后验状态估计值为

有机质热解生烃膨胀力和流体扩散力与源岩生烃率成正比，即生烃速率越大，产物增加的体积越大，形成的膨胀力和流体扩散力也越大［9-10］。随埋深增加，累积生烃量增加，源岩生烃速率逐渐增加，达到生油窗时生烃速率达到最大值，随后生烃速率逐渐降低（图6（b））；毛细管压力差呈现出先增加后降低的趋势，产物增容膨胀力和流体扩散力也呈现先增加，到一定程度又减小的趋势（图6（c））。

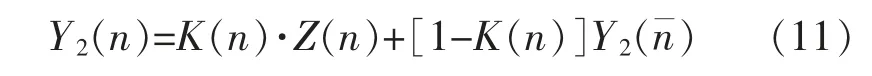
式中：Z（n）为n时刻的测量值。

然后，不断地迭代更新误差协方差P（n），即对P（n）值不断地修正：

最后，将经过新型卡尔曼滤波算法输出的2个相邻的数值做差，当差值≤系统设定值时，就认为数值稳定，可以输出显示与储存；如果差值>系统设定值，则继续循环取值滤波，同时，可以通过红外遥控对称重系统参数进行设定或自主校准。

2 试验测试

为了实现称重系统的质量采集功能，采用中航电测L6D 称重传感器作为称重前端。它是一个能够采集质量的高精度电阻应变式传感器，其量程为2.5～50 kg，精度为C3。

称重传感器输出的电信号通常比较微弱，需要将其放大再进行模数转换，由于A/D转换模块的位数越高，即对输入信号的分辨能力就越高，采用高位数模转换器在数据输出的精度上也更加可靠，所以，模数转换模块选用了24位的高度集成模数转换器ADS1232，其内部有高精度模数转换器ADC和仪表放大器PGA，不仅结合了模数转换和放大信号功能，而且减少了元器件的使用。

为了提升称重系统的实用功能，选用拥有大量I/O接口的STC12C5A60S2单片机作为称重系统的核心微处理，在称重系统中，需要对称重数据和设置操作的过程进行显示，LCD19264 全点阵液晶显示模块可以同时显示多位字符，且通过设置可以开启背光功能，为了保存称重数据和对称重系统发送的指令信息，设计称重系统储存电路，不仅要求储存和取值的速度快，而且容量大小需要满足系统存储需要，采用含有256个8位字节的24C256 作为称重系统的存储模块，适用于称重系统储存电路。红外线模块采用了一体化红外接收器HS38B和远程操控的遥控组成，可以对器件进行远程操控，设计的称重系统硬件如图2所示。

图2 称重系统硬件实物Fig.2 Weighing system hardware object

对称重系统滤波算法中的参数进行设置，状态转移参数A是用于将相邻2个时刻状态相联系的桥梁，在系统中认为相邻2个时刻的质量并无改变，故将状态转移参数A 设为常数1。由于构建符合称重系统的状态模型并无控制信号的参与，故将控制输入的增益B 设为0，根据状态变量和测量变量二者之间的比率，可以判定其增益H=1。

当参数确定后，需要对估计状态的输入信号值Y2（n）和误差协方差P（n）赋予初值。在设定初值时，若P（0）=0，表明此时环境中是无噪声的，不需要在进行滤波。由于卡尔曼滤波在每次迭代时均会产生新值，可以很快地修正不合理的数值，故将Y2（0），P（0）的初值分别设定为1，10。

3 试验结果

在滤波算法中，参数Q 负责控制滤波后的曲线平滑程度，参数R控制滤波后的曲线与真值曲线的相近程度。协方差Q和R的值由被观测的系统本身和测量过程中的噪声所决定，只能通过仿真试验观察其取值是否可以收敛到真值来确定，通过多次试验对比可知，当取Q=1×10-7，R=0.05时，系统的收敛程度是最优的。

采用多组测量质量来测试系统的线性度和灵敏度，在此分别使用10，15，20，25，30，35，40，45，50 kg 标准砝码，每个测量值均取5次测量后的平均值作为最后结果，在测量质量时，记录相应的A/D转换模块的输出电压，最终得到检测系统的输出电压与称重质量之间的关系，如图3所示。

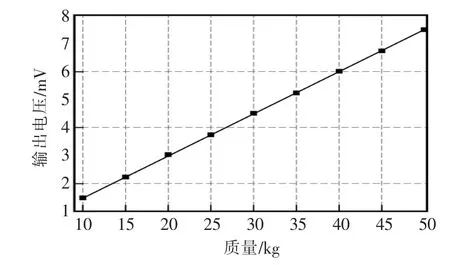
图3 质量与输出电压之间的关系Fig.3 Relationship between mass and output voltage

由图可见，当称重质量增加时，检测系统的输出电压也随之升高，并且检测系统的输出电压和质量可以保持较为理想的线性关系，有利于提高检测系统的测量精度，另外，可以计算出，在测量范围内系统的灵敏度约为0.15 mV/kg。

测量质量为30 kg时，在相同的条件下，快速测取20次经过新型卡尔曼滤波后的结果值和未经滤波的结果值，滤波前后的对比如图4所示。

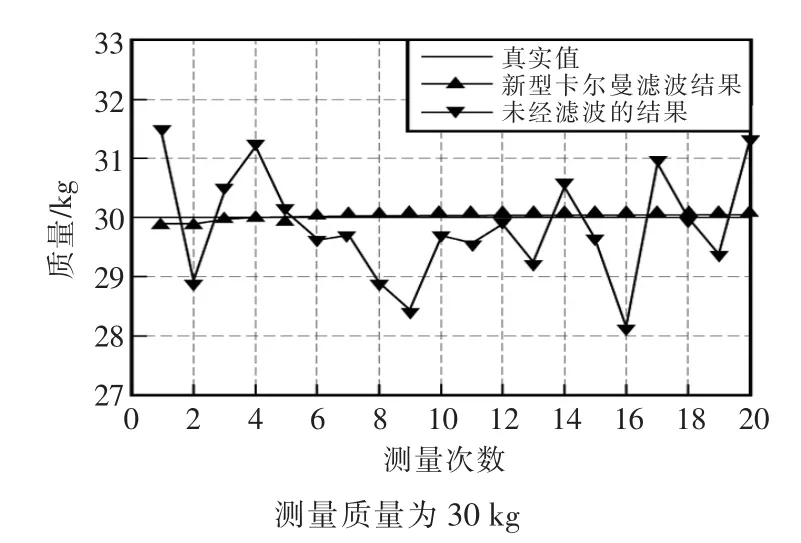
图4 滤波前后的测量结果Fig.4 Result graph before and after filtering

由图可见，未经滤波的结果与真实值30 kg对比，最大差值为1.86 kg，其中最大误差为6.2%，未经滤波的结果与真实值之间存在较大的浮动误差，而经过新型卡尔曼算法滤波后，最大差值为0.09 kg，最大误差仅为0.3%，经对比可知，新型卡尔曼滤波算法将系统精度提高到20倍，而且在使用了新型卡尔曼滤波算法后，数据曲线更加收敛于真实数据，平稳性也较高。

采用10 组不同质量的标准砝码，得到的测量数据和误差见表1，表中，C1为标准砝码的质量值；C2为经过卡尔曼滤波后的采样值；C3为经过改进的卡尔曼滤波的采样值；E1为经过卡尔曼滤波后与真实值的误差；E2为经过改进型的卡尔曼滤波与真实值的误差。

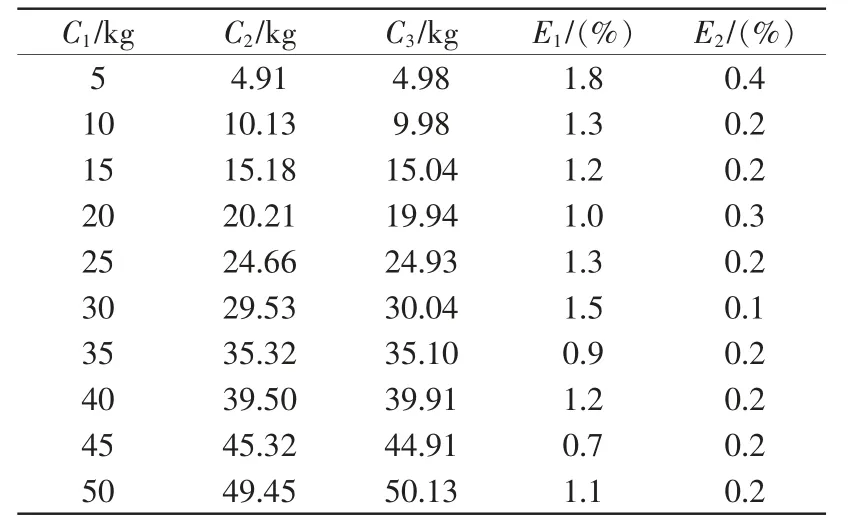
表1 滤波前后的测量数据及称重误差Tab.1 Measurement data before and after filtering and weighing error

由表可知，使用传统卡尔曼滤波算法对数据信号处理后，误差最大为1.8%；经过新型卡尔曼滤波处理后，误差均在0.4%以下，对比二者滤波处理后的数据误差可知，新型卡尔曼滤波算法将系统精度提高到4.5倍，可见新型卡尔曼滤波比传统的卡尔曼滤波的效果更好。

4 结语

所设计的基于新型卡尔曼滤波算法的称重系统，采用多种滤波方式结合的方式对采集信号进行处理，融合了各个滤波算法的优点，同时也相互弥补了对方滤波算法的缺点，试验结果表明，新型卡尔曼滤波算法不仅克服周期和非周期的脉冲干扰，而且减小了由于脉冲干扰所引起的采样值偏差，抑制了采集信号高斯白噪声，有效地提升了称重系统的精度。