基于图像质量与频谱特性加权的光瞳结构优化

赵晋炜，于 洵，龚昌妹，姜 旭

（1.西安工业大学 光电工程学院，西安710021；2.西安工业大学 西北兵器工业研究院，西安710021；3.西安应用光学研究所，西安710065）

随着信息科学的发展和光学加工制造技术的进步，高分辨率光学成像技术在军事侦察、目标监视、地形测绘、地表资源普查、灾情监测等领域的应用越来越广泛[1]，在工作波段一定的条件下，要提高望远成像系统的分辨率，只有增大系统口径，才能满足观测时对于角分辨率的要求，但是，系统孔径的增加不仅会造成加工检测难度和体积重量的增加，且导致加工成本的上升，近年来所提出的光学合成孔径成像技术在一定程度上解决了这一难题，其将多个孔径较小的光学系统按照特定排布方式组合在一起，便可获得与单个大孔径系统相当的空间分辨率，是实现大孔径光学系统的有效手段和发展方向[2]。

1 光瞳结构的优化方法研究

光学合成孔径成像系统与传统的光学成像系统不同：①合成孔径系统的PSF和MTF与系统子孔径间的阵列结构密切相关，不同的光瞳结构会对系统性能造成不同的影响；②合成孔径系统直接输出的是低对比度的混叠图像，必须通过后续的图像复原处理技术才能达到或接近单个大孔径系统的成像质量[3]，文献[4]基于图像重建误差最小化准则提出一种新的空间排列方式；文献[5]提出基于加权频段能量的优化方法，通过聚合典型光瞳结构中部分子孔径来提升系统成像质量；文献[6]给出实现最大分辨率的优化方法，并对9～21 孔径结构进行优化和分析，此外，文献[7-9]基于不同的优化准则设计了不同的光瞳结构，并对其调制传递函数的分布特性和复原图像质量进行分析。

以往对合成孔径系统的研究，主要集中在系统的光学性能指标上，在此基础上建立的光瞳结构优化准则可分为两类[10]：①以物空间某点发出的光在像空间的能量集中程度，作为系统成像质量的评价依据；②将光学系统对各种空间频率余弦分量的传递和反应能力，作为系统成像质量的评价依据，需要注意的是，合成孔径成像系统和传统成像系统的主要区别之一，是其严重依赖于对直接成像结果的后期图像复原过程，其成像性能通常由复原图像的质量来评价，依据以上优化准则得到的光瞳结构通常只能满足在特定方面的设计要求，不能直观地反映合成孔径系统的复原图像质量。

因此，需要进一步探究可以综合考虑光瞳结构性能的优化方法，以此为出发点，首先研究了3种典型六孔径光瞳结构的频谱分布特性和复原图像质量之间的关系，基于此提出了基于图像质量与频谱特性加权的光瞳优化方法；采用不同的权重因子分别对六孔径和九孔径光瞳结构进行优化，并将其复原图像质量和分辨率与3种典型光瞳结构进行对比、分析。

2 光学合成孔径成像系统的简化模型

光学合成孔径成像系统是由若干个圆形小孔径子系统按照特定排布方式组成的成像系统，其光瞳函数为[11]

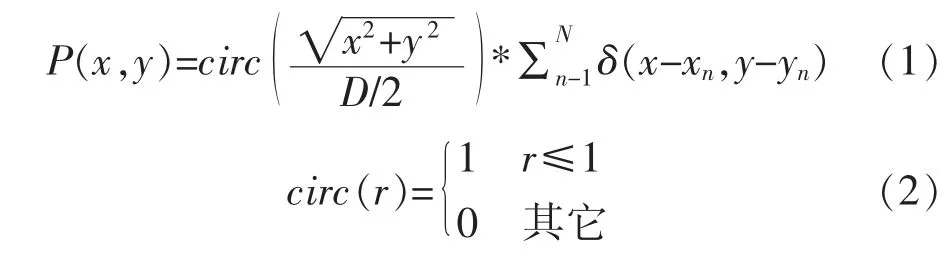
式中：circ（r）为圆域函数；D为子孔径直径；*为卷积运算符；N为子孔径数量；（xn，yn）为第n个子孔径的中心位置，系统的点扩散函数PSF（point spread function）和调制传递函数MTF（modulation transfer function）分别为

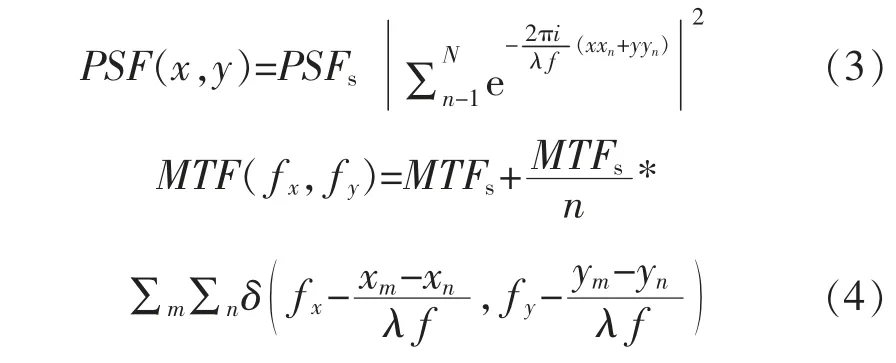
式中：PSFs和MTFs分别为单个子孔径的PSF和MTF；λ为系统工作波长；f为系统焦距，由式（4）可知，合成孔径成像系统产生的调制传递函数是由子孔径的调制传递函数组合而成，在工作波长和系统焦距一定的条件下，系统PSF的形状和MTF的分布情况与子孔径形状和子孔径阵列结构有关。

3 典型阵列的复原图像质量对比

以六孔径阵列结构为例，典型的合成孔径系统光瞳结构分为3种：环型、三臂型和Golay-6型。这3种光瞳结构的填充因子范围见表1[12]。

表1 三种典型光瞳结构的填充因子范围Tab.1 Filling factors range of three typical pupil structures

由表可知，不同的光瞳结构有不同的填充因子范围，为避免填充因子的差异对系统成像性能的影响，将填充因子F 固定为30%，得到上述3种典型光瞳结构及其对应的MTF分布如图1所示。

图1 三种典型阵列的光瞳结构与MTFFig.1 Pupil structure and MTF of three typical arrays

由于光学合成孔径系统直接接收到的图像是低对比度的混叠图像，为获得与等效单个大孔径系统相当的成像质量，必须对接收的图像进行图像复原的后处理[13]。对于光学合成孔径成像系统，通常采用维纳滤波器进行图像复原，表达式为

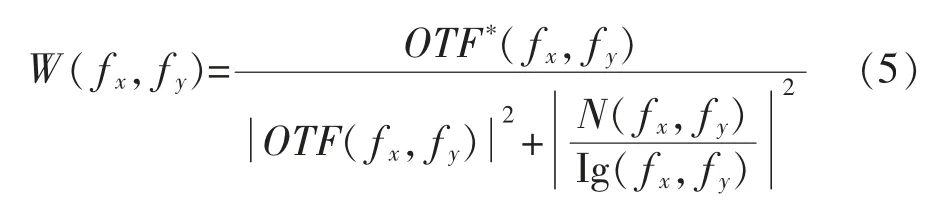
式中：OTF（fx，fy）为合成孔径成像系统的光学传递函数；OTF*（fx，fy）为其复数共轭；N（fx，fy）为噪声的频谱；Ig（fx，fy）真实图像的频谱。

在实际应用中，系统不可避免地会受到噪声的影响，系统总噪声的分布近似为零均值的高斯白噪声[14]，不失一般性，在此引入均值为0，方差为0.001的高斯白噪声，此时利用维纳滤波算法重建，得到3种光瞳结构的复原图像及局部细节放大图，如图2所示。

由其局部放大图（图2aⅡ，bⅡ，cⅡ）可见，环型光瞳结构的复原图像中存在大量伪影，Golay-6型和三臂型光瞳结构的复原图像分辨率相近，但前者的复原图像中存在较明显的噪声，且对比度较低，后者的复原结果更好。

采用信息熵E（entropy），峰值信噪比PSNR（Peak Signal to Noise Ratio）和结构相似度SSIM（Structural SIMilarity）3种常用的客观图像质量评价模型，对图2中的复原图像进行质量评价，以对比不同光瞳结构的复原图像质量。其中，E值越小说明图像越清晰；PSNR值越大，说明复原图像和原图像越接近；SSIM 从亮度、对比度和结构相似度这3个方面，综合评价两幅图像之间的相似程度，其取值范围为0～1，SSIM值越大，表示两幅图越相似[15]，其计算公式为

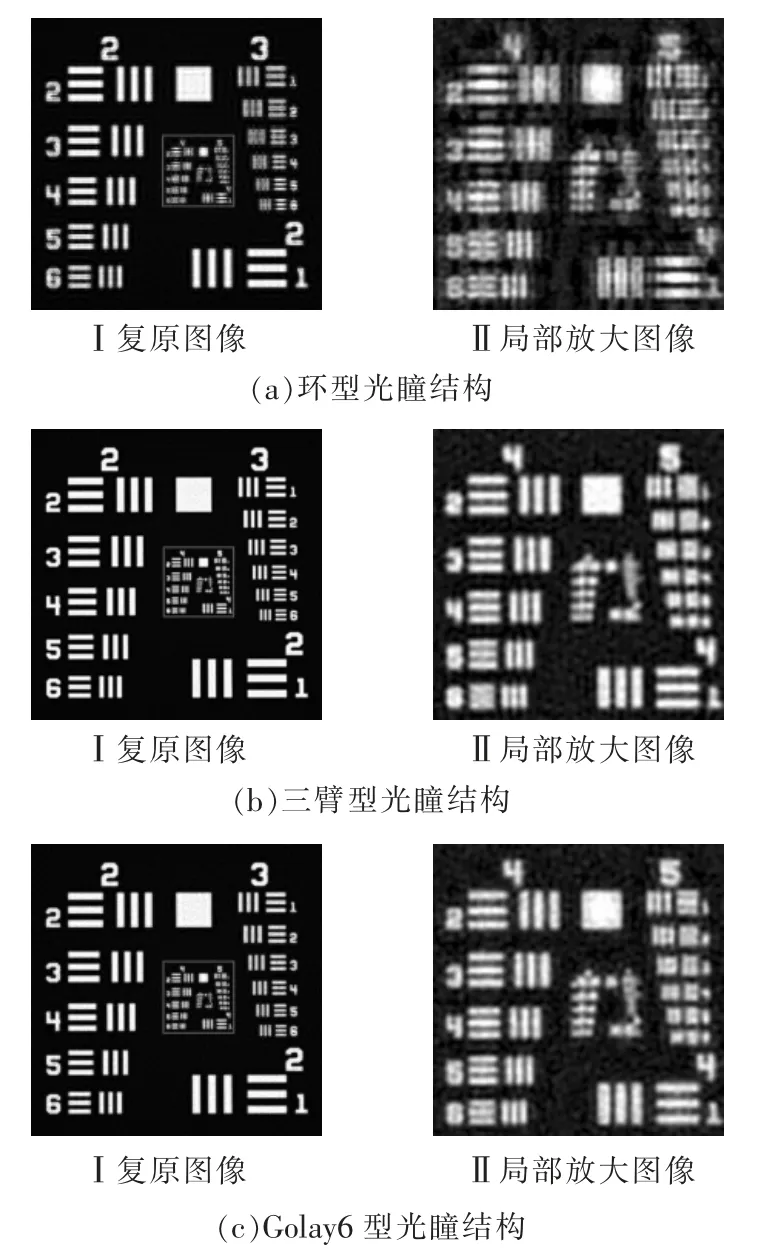
图2 三种不同光瞳结构的复原图像和局部放大图像Fig.2 Restoration images and local enlarged images of three different pupil structures

评价后所得的结果见表2。

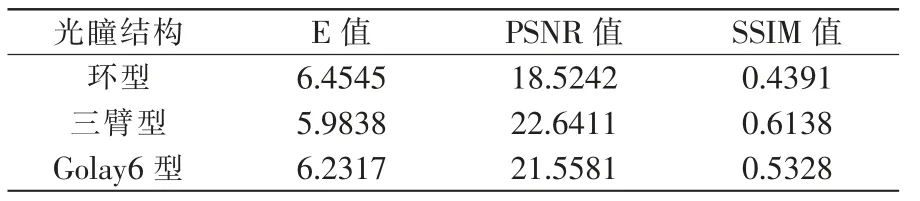
表2 复原图像的图像质量评价Tab.2 Image quality evaluation of restored images

由表可知，三臂型光瞳结构的复原图像质量评价结果最好，其次分别为Golay-6型和环型，这与图2是相吻合的，说明该图像质量评价结果较好地复原图像，其对比度更高、噪声水平更低。

采用对比不同光瞳结构间频谱差值图的方法，以探究导致不同光瞳结构复原图像之间差异的原因，得到三臂型、Golay-6型和环型相互之间的MTF差值图如图3所示。

由图3a，b 可见，差值图在边缘为负值，环型光瞳结构的MTF 频谱截止频率高于Golay-6型和三臂型，但是Golay-6型和三臂型在中低频具有更多的频谱信息；由图3c 可见，三臂型的截止频率略小于Golay-6型，但在中低频比环型有更多的频谱信息，结合图2中的局部放大图，可以推测，在有噪声条件下中低频信息更有利于抑制复原图像中的噪声，提高复原图像质量，更有利于人眼分辨。

图3 三种典型光瞳结构间MTF 差值图Fig.3 MTF difference diagram of three typical pupil structures

4 基于图像质量与频谱特性加权的光瞳优化方法

在优化合成孔径系统的光瞳结构时，目标函数的构建十分关键，不仅要考虑系统MTF的分布特性，还要综合考虑系统复原图像的质量，基于本文对复原图像质量与MTF 频谱特性之间关系的分析，在传统以MTF为优化准则的基础上，提出基于图像质量评价因子与频谱分布特性因子加权的光瞳结构优化方法，其目标函数为

式中：p1，p2，…，pn为子孔径中心位置；r为子孔径的半径；TMTF为频谱分布特性因子；γ为权重因子；M为图像质量的评价因子，该目标函数模型综合考虑了光瞳结构的复原图像质量和频谱分布特性，可使合成孔径系统MTF 在满足一定分布特性的同时，还能获得更好地复原图像质量。

在此，TMTF采用MTF的实际截止频率ρR，即MTF 第一次出现零值时所对应的空间频率，其大小决定了系统的分辨能力。ρR为

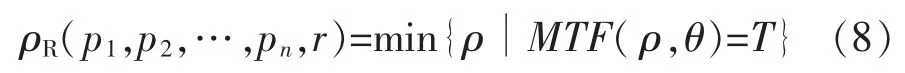
式中：T为预先设定合成孔径成像系统的MTF最小频率阈值，通常T=0.05；ρ，θ为极坐标系下的频谱坐标。

针对复原图像质量的评价因子M，在此采用SSIM 这一图像质量评价指标。该模型可从感知结构失真的角度评估2 幅复杂结构图像间的差异，更符合人眼对图像品质的判断，另外，需保证子孔径间无重叠，对应的约束条件为

式中：t为两子孔径边缘的最小间距，由于频谱分布的方向性会造成复原图像在不同方向上存在分辨率的差异，因此在优化时应保证MTF 在频谱面的各方向都具有相近的截止频率，即

式中：ρmax，ρmin分别为系统MTF 截止频率的最大值、最小值；ε为设定的阈值。

5 仿真结果与分析

光瞳结构优化时涉及的变量主要包括子孔径的半径和中心位置，利用常规求导方法难以对其优化，故在优化模型的基础上结合遗传算法，实现对光瞳结构信息的全域搜索和并行运算，在相同光瞳面积、填充因子为30%、不同权重因子（γ=0，100，200）的条件下，对六孔径光瞳结构进行了优化，通过优化，得到光瞳结构、频谱分布图、MTF 截面图、复原图像的局部放大图像，以及箭头处的扫描线，如图4所示。

图4 优化得到的六孔径光瞳结构Fig.4 Optimized six-aperture pupil structure

由图可见，当γ=0时，优化得到的六孔径光瞳结构的MTF 截止频率在0.8～0.9 之间，子午方向和弧矢方向的截止频率差值约为0.1，频谱分布近似为圆形且在频谱面内无零值，与3种典型六孔径光瞳结构的局部放大图（图2）相比，图4cⅠ中第5 组中第1个元素更为清晰，但与图2b，2c相比，图4cⅠ中的噪声较为明显。

当γ=100时，优化得到的六孔径光瞳结构（图4bⅡ）的中低频频谱信息比图γ=0时（图4bⅠ）更多，其复原图像（图4cⅡ）中噪声得到一定抑制，图像质量整体得到提升。

当γ=200时，所得的六孔径光瞳结构更集中，其MTF的截止频率（图4bⅢ）与γ=0时（图4bⅠ）相比有所下降，导致所得的复原图像分辨率也随之降低，但是，由于该光瞳结构在中低频有更多的频谱信息，图4cⅢ的图像质量要明显好于图4cⅠ，通过观察局部放大图中箭头所指处的扫描线可发现，图4dⅢ中前4 组三杆靶的对比度要明显大于图4dⅠ，说明其复原图像有更高的对比度，更有利于人眼分辨。

利用3种图像质量评价模型分别对以上光瞳结构的复原图像进行评价，结果见表3。

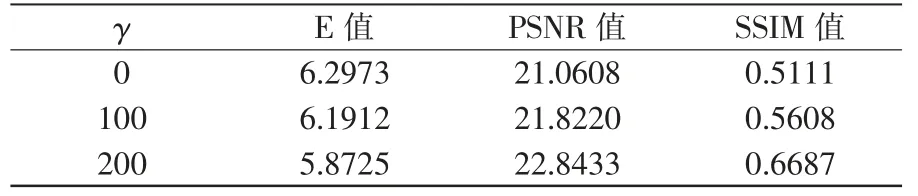
表3 优化的六孔径光瞳结构的复原图像质量Tab.3 Restored image quality of the optimized six-pupil structure

由表可知，随着γ的增大，复原图像的质量也随之提升，特别地，与γ=0时相比，γ=200时的E值下降了6.75%，PSNR值提升了8.46%，SSIM值提升了30.84%。

对比表2和表3 可知，在γ=200时，优化得到的六孔径光瞳结构的复原图像与环型、三臂型和

Golay-6型相比，其E值分别下降了9.02%，1.86%，5.76%；PSNR值分别提升了23.32%，0.89%，5.96%；SSIM值分别提升了52.29%，8.94%，25.51%，这说明，当γ=200时，优化得到的光瞳结构其成像性能，优于典型六孔径光瞳结构。

在相同条件下，利用该方法对九孔径光瞳结构进行优化，验证该方法的通用性，结果如图5所示。

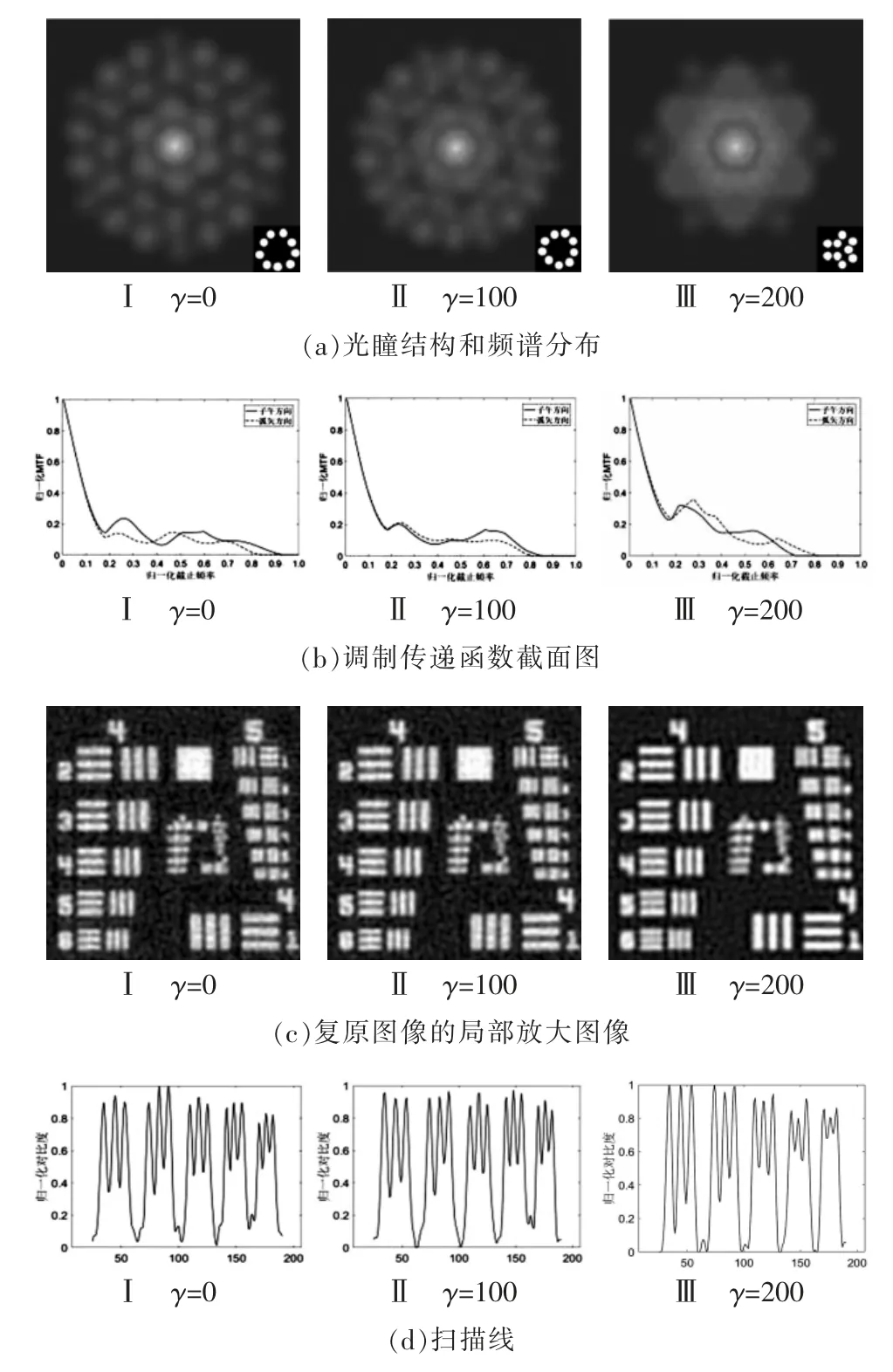
图5 九孔径光瞳排布Fig.5 Optimized nine-aperture pupil structure

由于九孔径光瞳结构中子孔径数量的增加和半径的减小，其排布方式更为灵活，随着权重因子的增大，九孔径光瞳结构中部分子孔径向中心聚合（图5aⅢ），使系统在中低频可获得更多频谱信息，有利于系统在保持较高分辨能力的同时，拥有较好的复原图像质量。

表4 优化得到的九孔径光瞳结构的复原图像质量Tab.4 Restored image quality of the optimized nine-pupil structure

对比表3和表4 可知，当填充因子相同时，在相同权重因子下优化得到的九孔径光瞳结构的复原图像质量，与六孔径基本相同，仿真结果表明，该方法同样适用于九孔径光瞳结构的优化。

6 结语

通过对3种典型六孔径光瞳结构的复原图像质量和频谱分布特性进行对比分析和研究，发现复原图像质量较好的光瞳结构在中低频有更多的频谱信息，基于此，提出了一种基于图像质量评价因子与频谱分布特性因子加权的光瞳优化方法，其可在满足频谱分布特性的同时获得更好的复原图像质量，仿真结果表明，采用合适的权重因子优化得到的光瞳结构可获得更好的复原图像质量，从而可以更好地满足实际应用。