基于万能运动参数的弧齿锥齿轮建模方法
唐祎,何玉辉,唐进元
(1.中南大学机电工程学院,湖南长沙,410083;2.中南大学高性能复杂制造国家重点实验室,湖南长沙,410083)
在现代化机械制造业尤其在汽车、航空和机床中,弧齿锥齿轮生产占有重要地位。由于齿面几何形状的复杂性和特殊性,弧齿锥齿轮不存在统一标准的齿面参数化表达。弧齿锥齿轮的齿制、加工方法、加工机床、加工工艺都各有不同,故有多种分类方式,例如按照齿高分类,可分为等高齿锥齿轮、渐缩齿锥齿轮和双重收缩齿锥齿轮;而按加工机床分类,又分为带凸轮机构机械式摇台机床和五轴联动数控机床。机床不同,则对应的基本加工工艺也不同。例如,在传统的GLEASON 机械式摇台机床No.116 上加工,一般采用五刀法,即大轮粗加工+大轮精加工和小轮粗加工+小轮凹面精切+小轮凸面精切。一直以来,齿面建模都局限于某一类加工调整卡(如SGM,HGM 等)和某一类加工机床进行加工过程仿真模拟[1]。加工调整卡、加工工艺发生改变,都需要重新针对复杂加工过程进行建模,计算过程复杂,建模效率低,通用性差。本文突破传统建模,基于弧齿锥齿轮设计的万能运动概念(UMC),提出了基于万能运动参数的通用建模方法。其中,UMC 机床模型是针对数控加工,将传统摇台机床各轴“数控化”后的一种机床模型,既能实现传统机床的功能,又能利用“数控化”后各轴的运动能力来实现相应的齿面误差修正。在通用加工参数的齿面建模中,通过8个通用参数可以转化成任意机械式加工机床的调整卡参数,完成任意调整卡、任意加工方法的通用统一仿真模拟。目前,有关UMC 建模的研究比较少,GONZALEZPEREZ 等[2-3]提出了改善齿面接触特性的齿面综合分析方法及齿面综合优化的数学模型,针对各种误差对运动精度的影响进行解析描述;ARTONI等[4]对万能运动概念进行了阐述,但没有进行基于UMC 建模的研究;FAN[5-6]结合UMC 的基本概念对弧齿锥齿轮进行了建模与仿真,并推导了一套刀具相对于齿坯的坐标变换关系;唐进元等[7-12]在弧齿锥齿轮的通用化设计和加工方面进行了大量研究,内容涉及弧齿锥齿轮基于各种调整卡的建模与TCA 和LTCA 分析,为齿面几何精确建模打下基础;LIN 等[13-14]研究了通用加工参数与机械式机床参数之间的等效转换关系。综上所述,上述研究均没有给出基于万能运动参数的弧齿锥齿轮通用建模方法。本文针对这一问题进行研究,给出基于万能运动参数的弧齿锥齿轮通用建模方法,通过相关计算实例对方法进行验证。
1 齿面通用数学模型
基于确定的通用机床加工参数采用真实齿面加工仿真模拟的设计理念,建立满足齿面啮合原理的方程,完成齿面数学建模,借助数值求解方法完成齿面点的离散化,得到齿面的真实模型。
1.1 刀具建模
弧齿锥齿轮建模来源于实际齿轮加工过程的仿真模拟[4]。通过数值模拟刀盘与工件的加工运动轨迹,获得一系列不同时刻的刀具曲面簇。齿面由刀具轨迹的曲线族包络而成,获得的每一个齿面点必定满足齿面啮合定理,求导得由刀具切削轨迹包络而成的齿面参数化方程为
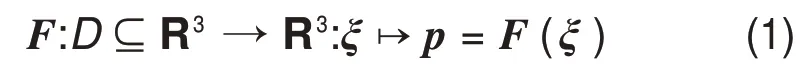
式中:ξ=(μ,θ,φ)为基本设计参数[15],包含刀盘刀具的几何参数(μ,θ)和机床运动基本参数φ;μ为刀具高度方向的变量;θ为刀具旋转角度。该仿真过程主要包括刀盘刀具设计(与几何参数(μ,θ)有关)和机床运动设计(与由φ表示的机床加工参数有关)。
刀盘刀具设计主要包括3种类型:直线型、抛物线型和Top-Rem型。而在UMC建模中,抛物线型刀具如图1所示,分为2个部分。
1)上端圆弧部分参数化方程:
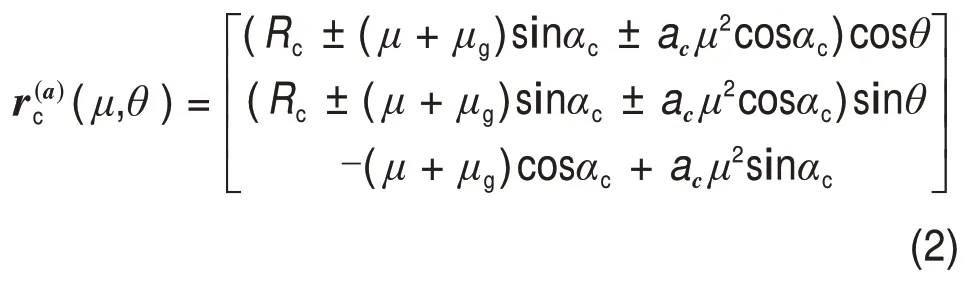

图1 抛物线型刀具形状Fig.1 Type tool shape of parabolic-profile

2)下端圆弧部分参数化方程:
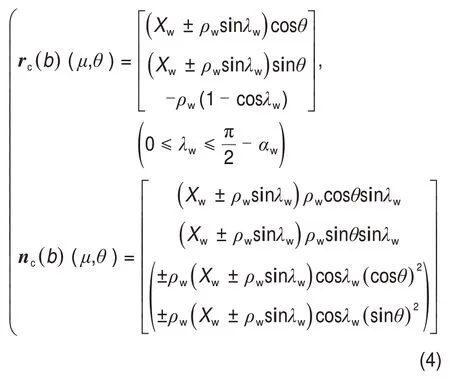
式中:Rc为刀位点半径;μg为抛物线顶点位置参数;ac为抛物线系数;αc为压力角;ρw为刀盘边缘半径;λw为刀盘边缘圆弧角度;Xw为Oc与C点的连线长度;“+”和“-”分别为齿轮加工的凹面和凸面。
1.2 基于刀具展成运动的齿面通用数学模型
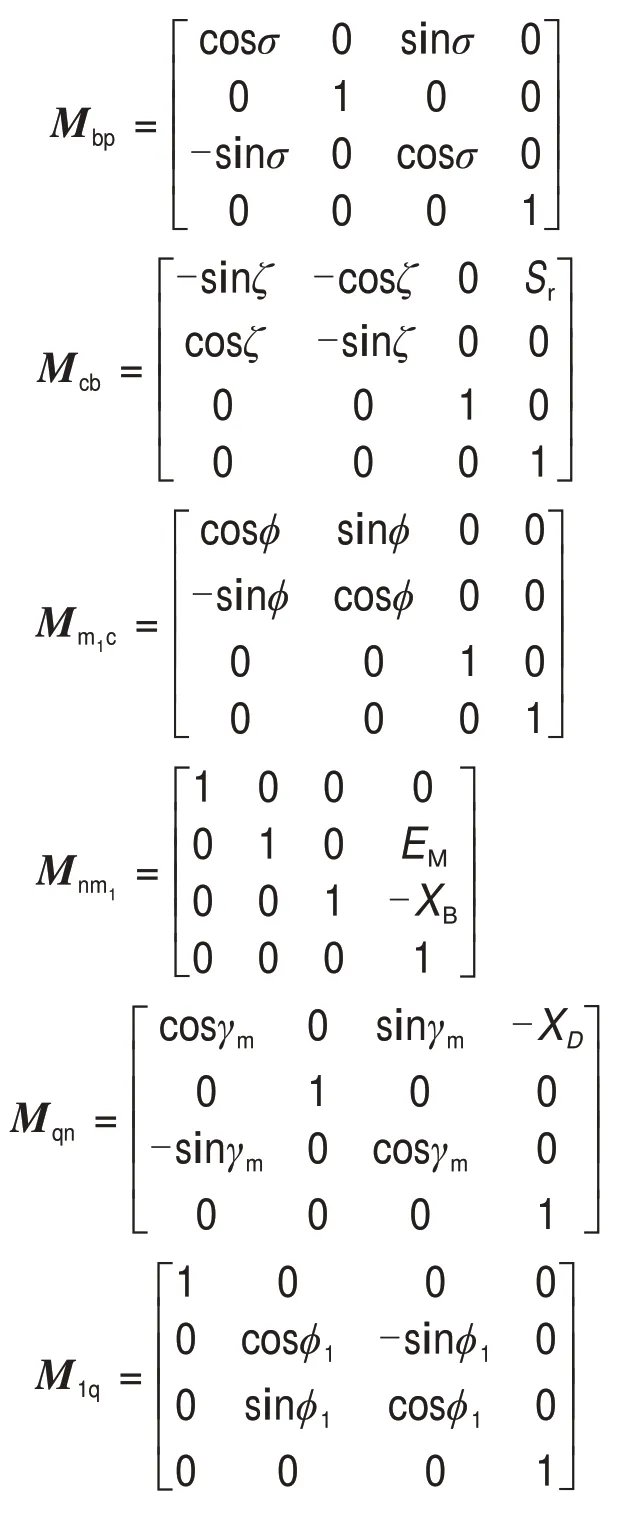
图2所示为基于UMC 的机床运动关系参数设置。参照Gleason公司基于万能运动概念的设计理念[9]和万能展成模型[13],在UMC 或者UGM 框架中,有8 个万能运动参数[16],分别是刀位Sr、垂直轮位EM、水平轮位XD、床位XB、根锥安装角γm、刀倾角б、刀转角ξ和基本摇台角φ,即

它们各自可以表示为关于最基本的运动参数φ的高阶多项式函数。例如,床位XB就可以表示为

式中:XBk(k=0,…,n)表示其k阶运动系数。利用万能运动参数就可以表示从齿坯到刀盘的整个机床运动链所有坐标转换关系Mbc,有

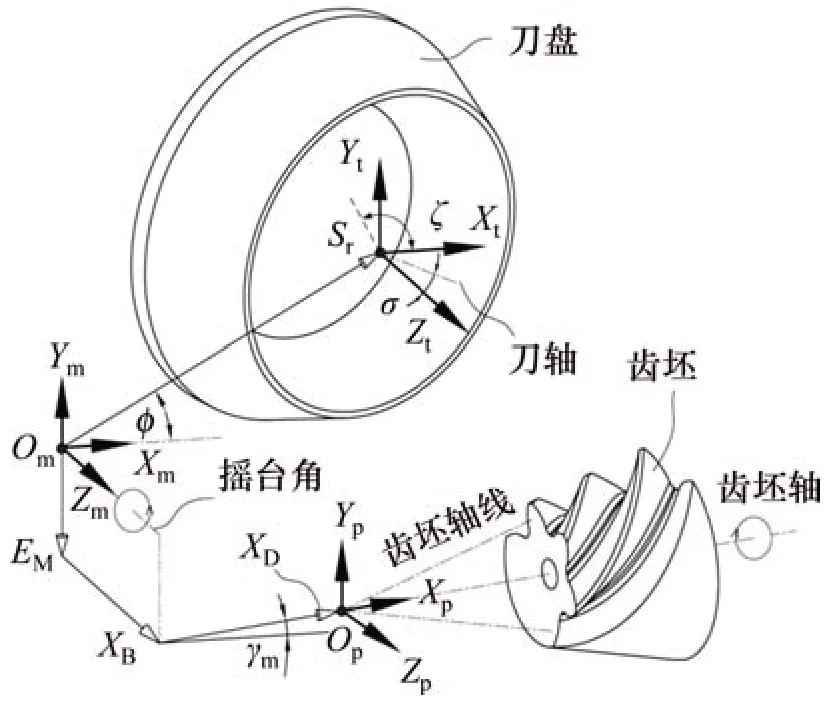
图2 基于UMC的机床运动关系参数设置Fig.2 Parameter setting of UMC-based machine motion relationship
其中:
因此,展成齿面可表示为

由于齿面是由刀具轨迹的曲线簇包络而成,故获得的每一个齿面点p*=F(ξ*)必定满足齿面啮合定理[9],可得

式中:nb为齿面的方向矢量;而vbc为加工过程中刀具与齿坯的相对速度。联立式(8)和(9),可完成齿面方程的隐式表达。显然,该方程组中,含有3个未知变量和2个标量方程,具有很强的非线性和复杂性,通过研究高效率的数值求解方法,即可以求出展成包络齿面数值点。
2 齿面离散化方法及实例
2.1 齿面离散化方法
通过齿面离散化获得理论齿面坐标点,以便与实际加工齿轮测量点进行对比。在齿面建模中已经证明:齿面参数化方程的非线性和复杂性导致齿面不能以显示形式表示出来,如
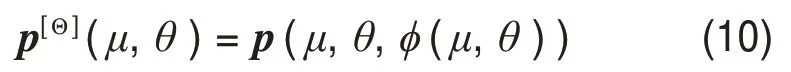
只能进行齿面离散化逐点求解。通过离散其中1个未知参数,求解以另外2个参数构成的精确齿面方程,匹配合理的齿面等分均匀化规则[17-18],以前锥面、背锥面、顶锥面和根锥面为约束边界条件,就可以完成齿面网格化离散过程。
2.2 齿面建模实例
根据提出的建模方法,结合万能运动概念,由8 个万能运动参数控制刀具相对齿坯的运动轨迹,完成对所有弧齿锥齿轮的参数化建模。以下算例将不同的弧齿锥齿轮副机床加工参数输入至求点程序,可分别得到规律的齿面离散点坐标,并直接利用齿面离散点建立参数化曲面,在CATIA中构建对应的实体模型。
2.2.1 齿面建模
本文采用Gleason No.116机床HFT调整卡双面法加工的弧齿锥齿轮副基本设计参数,主要包括齿坯设计参数和机床加工参数。需要强调的是,根据UMC 定义,原本刀倾法(Tilt®)调整卡加工的11个机床加工参数除了表中所给万能运动参数外,还有压力角αc和刀盘偏心角βc,都可以转换成万能运动参数。根据本文提供的通用参数化建模方法,可建立齿面的数学模型,并完成齿面的离散化表达。
2.2.2 算例
由于弧齿锥齿轮副的加工工艺繁杂,本文选取其中的主要加工工序即铣齿加工来完成齿轮三维实体建模。在弧齿锥齿轮的齿面啮合方程求解过程中,代入不同数值的万能运动参数,由MATLAB 求解程序可获得一系列均匀分布的离散齿面点。表1所示为齿坯参数,表2所示为机床加工参数。
根据给定的齿坯参数与机床加工参数即可完成齿面方程的推导,求解出规律分布的齿面离散点坐标,需说明的是,由于建立的齿面方程具有非线性,不能直接推导出显示的齿面方程表达式,只能借助齿面参数化方法将齿面表示成离散化的点,其中采用的是9×15 的网格点分布方式,如图3所示。

表1 齿坯参数Table 1 Blank parameters

表2 机床加工参数Table 2 Machine-tool settings
本文提出的参数化建模求解齿面点的优点在于:与Gleason 求解齿面离散点的cage 软件类似,能求得一系列有规律、光顺的齿面点,有利于后续进行实体建模;齿面点之间的间距可人为控制;齿面点的密度可根据齿面面积人为设定。
2.3 弧齿锥齿轮实体建模
根据Matlab 求解的齿轮副的齿面离散点反映出齿面具有良好的齿面光顺性和连续性,可为后续齿面误差测量及修正、齿面接触分析(TCA)等关键技术提供精确齿面模型和基本数据信息。在弧齿锥齿轮三维建模过程中,齿面离散点必须规则化,不能出现奇异点或者散乱点,且齿面点分布越密集,得到的模型精度越高。图4所示为齿轮副在CATIA 中的实体模型,将获得的离散齿面点坐标导入CATIA 中,由点构线,由线构面,分别构造弧齿锥齿轮的凹面与凸面,再与齿根圆锥面相交进行修剪可得到1个齿槽模型,最后由齿槽与齿坯实体进行布尔运算,即可得到弧齿锥齿轮三维建模。
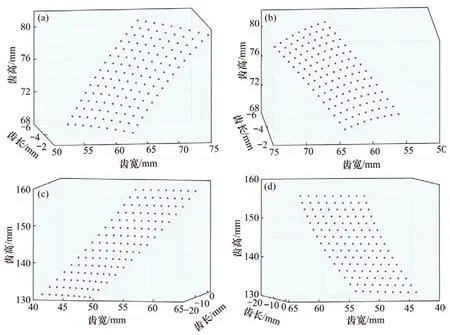
图3 离散化齿面点Fig.3 Discretized tooth surface points
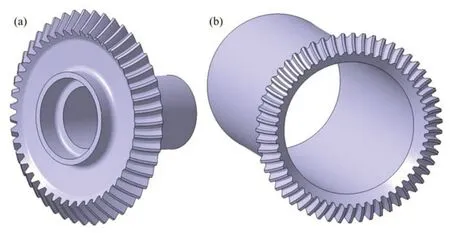
图4 齿轮副在CATIA中的实体模型Fig.4 Physical model of bevel gear pair in CATIA
3 齿面误差测量及结果分析
3.1 齿面误差的精确测量
在实际加工过程中,受多种因素如装配、机床运动、热处理变形和磨损和装夹等影响,实际加工制造的真实齿面与理论齿面产生一定偏差。在弧齿锥齿轮的齿面设计中,定义其法向偏差为齿面误差,用差曲面来表示。在目前的实际测量中,很多公司有专门的齿轮测量仪,配备专业商用软件如G-AGETM和KOMET®等,完成齿面的精确自动测量。本文采用CMMs 精确测量弧齿锥齿轮的齿面误差,CMMs 具体型号为1500GMM,测量参考标准为HB0-1992-1998。图5所示为齿轮副的实际加工齿面误差CMM测量实例。

图5 实际加工齿轮的CMM测量Fig.5 CMM measurement of actual machined gears
3.2 齿面误差的测量结果
在齿面测量规划中,将齿轮的轴向横截面预设1 个齿面网格AMBMCMDM,该齿面网格可以根据齿面离散化来确定,用来表示1个理论参考的设计齿面。参照Gleason标准的一般齿面预设网格点规划,齿面被离散化成1个典型的5×9网格,即齿宽(face width, FW)方向取9 个点,而齿高( tooth height,TH)方向取5 个点,并建立与理论齿面的差曲面。图6所示为三坐标测量仪测得齿面误差。
表3所示为齿面误差测量结果。将建立的齿轮模型与实际加工齿轮模型进行比较可知:小轮铣齿后的凹面齿面误差平均值为1.862 μm,最小值为-4.400 μm,位于(5,9)点即大端面与齿顶面相交处;最大值为5.100 μm,位于(5,4)点即靠近齿根面中间处;小轮凸面齿面误差平均值为5.236 μm,其中最小值为-9.700 μm,位于(2,1)点即小端面中间位置;最大值为13.400 μm,位于(5,9)点即靠近大端面与齿顶面相交处。
大轮的测量结果相比于小轮来说更理想,大轮凹面齿面误差平均值为2.328 μm,其中最小值为-5.200 μm,位于(3,2)点即靠近小端面中间处;最大值为3.200 μm,位于(4,9)点即大端面靠近齿顶面相交处。大轮凸面齿面误差平均值为1.477 μm,最小值为-2.600 μm,位于(3,2)点即靠近小端面中间处;最大值为3.400 μm,位于(5,1)点即小端面与齿顶面相交处。
3.3 齿面误差测量的结果分析
由表3可知:由于大轮是主动件且易加工,在实际加工制造过程中,可通过1次装夹同时铣削出凹凸面,而小轮则需分别装夹并使用不同种型号铣刀切削才能得到。这也解释了与较大轮相比,小轮齿面误差总体偏大的原因。其次,影响齿面精度的因素除了安装误差、装夹误差外,还应考虑到机床空间几何误差、刀具磨损等。
在实际建模过程中发现,使用Matlab 求解离散齿面点坐标时,离散的齿面点疏密程度也会影响三维模型的精度。
将求解的齿面点导入至CATIA 中,采用不同的方式构造三维齿面,获得的实体模型精度也会有所区别。例如,将9列的齿面点连成线再构面和将15行的齿面点连成线再构面得到的齿面不一样;在CATIA 创成式外形设计模块中,选择“桥接曲面”和“多截面曲面”命令创建的齿面也会有差异。
综合考虑制造加工过程中以及参数化建模流程中各种误差的的影响,在齿面法矢方向得到的齿面误差测量结果精度较高,说明本文提出的基于参数化弧齿锥齿轮通用建模方法原理正确。

图6 齿面误差分析Fig.6 Tooth surface error analysis
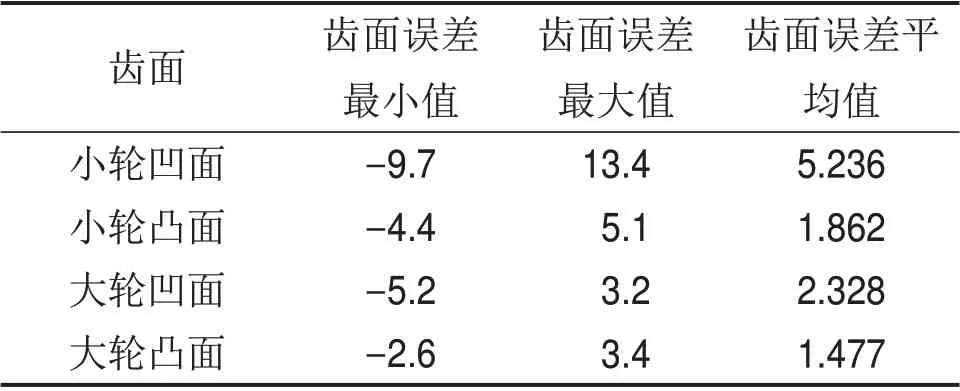
表3 齿面误差测量结果Table 3 Tooth surface error measurement results μm
4 结论
1)运用Newton 迭代法建立齿面参数化方程以获得统一齿面参数化表达,综合考虑机床几何空间误差、安装误差等误差来源,提出基于万能运动参数的弧齿锥齿轮建模方法。
2)对1对锥齿轮参数进行模型建立,测量结果显示建立理论模型与实际模型非常接近,为后续齿面误差修正提供基本的技术支撑和理论基础。
3)基于万能运动建模理念,给出了由万能运动参数驱动的齿面参数化模型。该机床加工参数可以由任意机械式加工机床调整卡参数转化而成,实现了所有加工形式统一的参数驱动化弧齿锥齿轮建模。

