时间序列季节调整技术比较研究

闵 盈 盈

(哈尔滨商业大学 计算机与信息工程学院， 哈尔滨150028)

时间序列中有些序列存在明显周期变化，这个周期就称为季节性.季节性可以是月度、周度或季度变化，这样的序列被称为季节性序列.在经济领域这样的季节性序列随处可见，季节性的存在给经济问题研究带来困难，带有季节变化因素的经济变量不能直接来计算环比增长率，只有分离季节因素才能更清晰、更快、更准确的反应经济变量变化，X-12-ARIMA与TRAMO/SEATS方法都是目前比较流行的季节调整方法，但是两种方法的优劣还是比较明显的，虽然两种方法都是建模、季节调整和诊断的过程，但是在很多细节方面侧重点不同，如：TRAMO/SEATS方法能够更加有效的处理序列的异常值，能够处理时间长达十五年以上的数据，而且回归拟合效果较好；X-12-ARIMA方法的模型诊断更加完整，通常处理时间较短的序列效果好，用其进行季节调整也更加接近真实值.所以两种方法均可以对具有季节性的时间序列数据进行处理，下面以苏宁电器2005～2017年的销售数据为例比较以下两种方法[1].

1 季节性时间序列的识别与特征分析

1.1 SNDQ序列特征分析

本文所有数据来源于《中国统计年鉴》、《EPS全球统计数据/分析平台数据库》以及上市公司年度报表，季节调整需要8年以上的样本长度才能取得较好调整效果，选取苏宁电器2005年1月～2017年12月的季度数据如表1所示，并把序列命名为SNDQ.

表1 苏宁电器销售量数据

如图1所示，从1978～2017年苏宁电器销售量一直都是上升趋势，并保持线性增长态势，2005～2006年增长较为缓慢，2006年后增长迅速 ，如表2所示增长率最高的年份为2006年第一季度达到118%.增长率最低为2015年第四季度是-24%.对时间序列进行分析要求序列必须平稳，下面对序列进行平稳性检验[2].

图1 苏宁电器销售量序列图

年月增长率/%年月增长率/%年月增长率/%200501392009023201304-16200502-18200903232014010.4720050317200904-22014024820050421201001520140317200601188201002-1201404-192006025201003-1320150114200603302010042201502-920060441201101120150337200701472011026201504-24200702-220110382016011620070310201104-10201602-520070413201201-4201603272008014820120230201604-16200802-82012031820170124200803-8201204-1820170242008042720130132017031620090129201303-32013020.03

1.2 SNDQ序列平稳性检验

如图1所示苏宁电器销售量序列曲线呈上升趋势，不是平稳序列，作如下检验，如表3所示ADF检验结果：原假设为有单位根，概率较大，T=-1.829 072检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如表4所示DF检验结果：原假设为有单位根 ，T=-2.076 854检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如表5所示LM检验结果是：原假设为序列是平稳的，T=0.110 877检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设存在单位根，原序列不平稳[3].

表3 苏宁电器销售量序列ADF检验

表4 苏宁电器销售量序列DF检验

表5 苏宁电器销售量序列LM检验

1.3 SNDQ序列差分及检验

不平稳序列需要进一步差分.如图2所示为差分后的序列.图中苏宁电器销售量差分后序列曲线在零点处上下波动，说明差分后的序列近似一个平稳序列，下面做检验，如表6所示ADF检验结果：原假设为有单位根，概率较大，T=-3.135 059检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设不存在单位跟，原序列平稳.如表7所示DF检验结果：原假设为有单位根，T=-3.208 377检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设不存在单位跟，原序列平稳.如表8所示LM检验结果：原假设为序列是平稳的，T=0.302 454检验量在1%、5%、10%的基础上均大于临界值，接受原假设，原序列平稳.下面对平稳后的序列进行季节调整和建模[4-5].

t-StatisticProbAuqmented Dickey-teler statistic-3.135 0590.930 7Test critical values1%level-3.077 7235%level-2.925 16910%level-2.600 658

表7 苏宁电器销售量差分后DF检验

表8 苏宁电器销售量差分后LM检验

2 X-12-ARIMA季节调整方法研究

2.1 应用X-12-ARIMA对原序列季节调整

应用X-12-ARIMA对原序列进行季节调整.如图3所示调正后分离出趋势循环成分、季节因子、不规则成分、季节调整后序列，季节调整后的序列图仍然是向上趋势，需要进行平稳性检验[6].

2.2 X-12-ARIMA季节调整后序列平稳性检验

应用X-12-ARIMA对序列季节调整后，需要进行平稳性检验，采用ADF、DF和LM检验，检验结果如表9～11所示.

图3 苏宁电器销售量X-12季节调整的不规则、季节、趋势循环、季节调整后序列

表9 苏宁电器销售量季节调整后ADF检验

表10 苏宁电器销售量季节调整后DF检验

表11 苏宁电器销售量季节调整后LM检验

如图7所示苏宁电器销售量数据经过季节调整后序列曲线呈上升趋势，这不是一个平稳序列，如表9所示ADF检验结果：原假设为有单位根，概率较大，T=-2.110 907检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如图10所示DF检验结果：原假设为有单位根 ，T=-2.230 501检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如图11所示LM检验结果：原假设为序列是平稳的，概率较大，T=0.107 674检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设存在单位根，原序列不平稳.对于不平稳的序列需要进一步差分[7].

2.3 X-12-ARIMA季节调整后差分序列平稳性检验

应用X-12-ARIMA对序列季节调整后进行差分，差分后序列图如图4所示.

图4 苏宁电器销售量季节调整后差分图及对比图

如图4所示季节调整后前后序列的差分对比图.圆点线为季节调整后的曲线，差分后序列图在零点附近上下波动，相比季节调整前趋于平稳，进一步做ADF、DF和LM检验，如表12～14所示.

表12 苏宁电器销售量季节调整差分后ADF检验

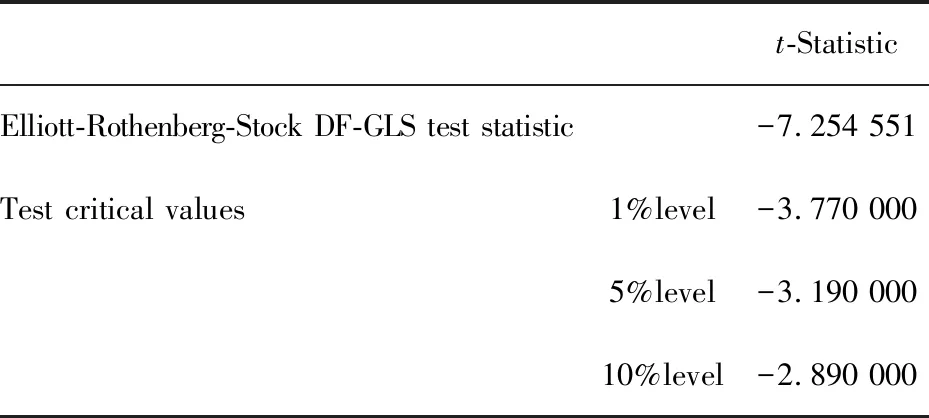
表13 苏宁电器销售量季节调整差分后DF检验

表14 苏宁电器销售量季节调整差分后LM检验

如图4所示苏宁电器销售量季节调整差分后的序列曲线在零点处上下波动，说明差分后序列是一个平稳序列，如表12所示ADF检验结果：原假设为有单位根，T=-7.182 427检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设不存在单位根，原序列平稳.如图13所示DF检验结果：原假设为有单位根，T=-7.254 551检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设不存在单位根，原序列平稳.如表14所示LM检验结果：原假设为序列是平稳的，T=0.179 205检验量在1%、5%、10%的基础上均大于临界值，接受原假设存，原序列平稳.平稳后的序列可以进行季节调整和建模[8].

3 TRAMO/SEATS季节调整方法研究

3.1 应用TRAMO/SEATS对原序列季节调整

下面应用TRAMO/SEATS方法对苏宁电器销售量数据进行季节调整处理.处理结果如图5所示.

3.2 TRAMO/SEATS季节调整后序列平稳性检验

对经TRAMO/SEATS季节调整后序列进行ADF、DF和LM检验，如表15～17所示.

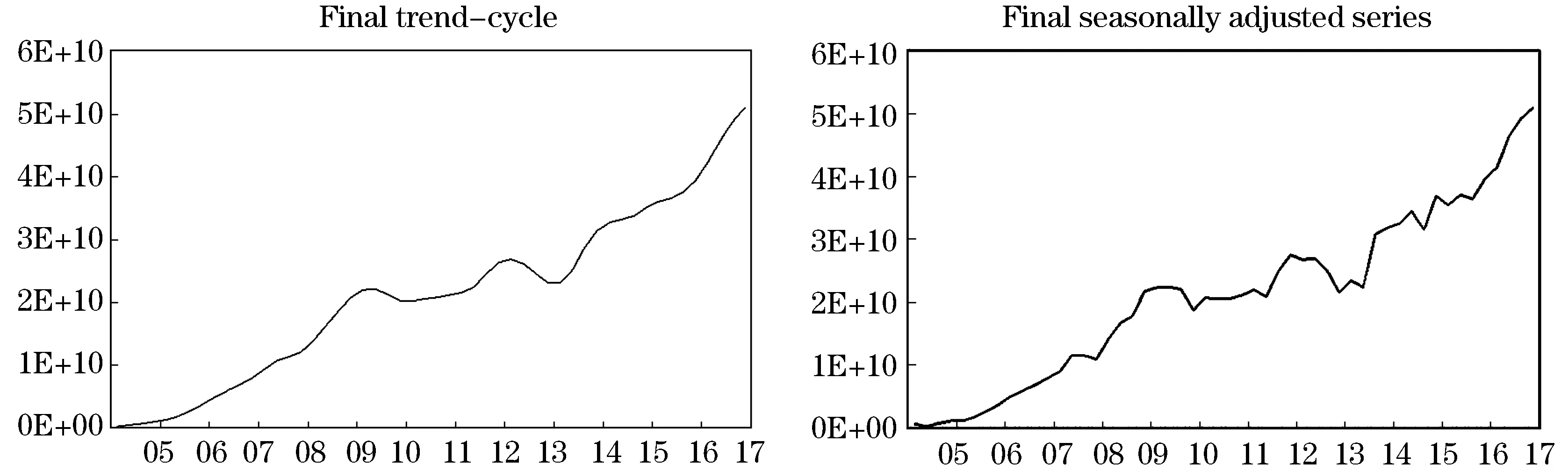
图5 苏宁电器销售量TRAMO/SEATS季节调整后趋势成分和季节调整后序列

如图5所示苏宁电器销售量序列曲线经过TRAMO/SEATS季节处理后呈上升趋势，这不是一个平稳的序列，如表15所示ADF检验结果：原假设为有单位根，概率较大，T=0.644 836检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如表16所示DF检验结果：原假设为有单位根，T=-1.998 183检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如表17所示LM检验结果：原假设为序列是平稳的，T=0.109 416检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设存在单位根，原序列不平稳[9].

表15 苏宁电器销售量TRAMO/SEATS季节调整后ADF检验

表16 苏宁电器销售量TRAMO/SEATS季节调整后DF检验

表17 苏宁电器销售量TRAMO/SEATS季节调整后DF检验

如图5所示苏宁电器销售量序列曲线经过TRAMO/SEATS季节处理后呈上升趋势，这不是一个平稳的序列，如表15所示ADF检验结果：原假设为有单位根，概率较大，T=0.644 836检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如表16所示DF检验结果：原假设为有单位根，T=-1.998 183检验量在1%、5%、10%的基础上均大于临界值，接受原假设存在单位根，原序列不平稳.如表17所示LM检验结果：原假设为序列是平稳的，T=0.109 416检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设存在单位根，原序列不平稳[10].

3.3 TRAMO/SEATS季节调整后差分序列平稳性检验

对于不平稳序列需要进一步差分.差分后的序列图如图6所示.差分后图像在零点附近上下波动，说明其已经平稳，进一步做ADF、DF和LM检验，如表18～20所示.

如图6所示苏宁电器销售量差分后的序列曲线在零点处上下波动，如图6所示季节调整前后的对图，细实线为季节调整前曲线，圆点线为季节调整后曲线，调整后序列趋于平稳，说明差分后的序列是一个平稳的序列，如表18所示ADF检验结果：原假设为有单位根，T=-7.812 151检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设不存在单位根，原序列平稳.如表19所示DF检验结果：原假设为有单位根，T=-7.956 007检验量在1%、5%、10%的基础上均小于临界值，拒绝原假设不存在单位根，原序列平稳.如表20所示LM检验结果：原假设为序列是平稳的，T=0.947 957检验量在1%、5%、10%的基础上均大于临界值，接受原假设存，原序列平稳.平稳后的序列可以建模[11-12].

图6 苏宁电器销售量TRAMO/SEATS季节调整后差分图及对比图

表18苏宁电器销售量TRAMO/SEATS季节调整差分后ADF检验

表19 苏宁电器销售量TRAMO/SEATS季节调整差分后DF检验

表20 苏宁电器销售量TRAMO/SEATS季节调整差分后LM检验

4 X-12-ARIMA与 TRAMO/SEATS季节调整结果比较

以上分别应用X-12-ARIMA与 TRAMO/SEATS季节调整方法[13]，以苏宁电器销售量为例进行研究，那种方法更适合这个序列的建模，下面进行比较如图7所示.

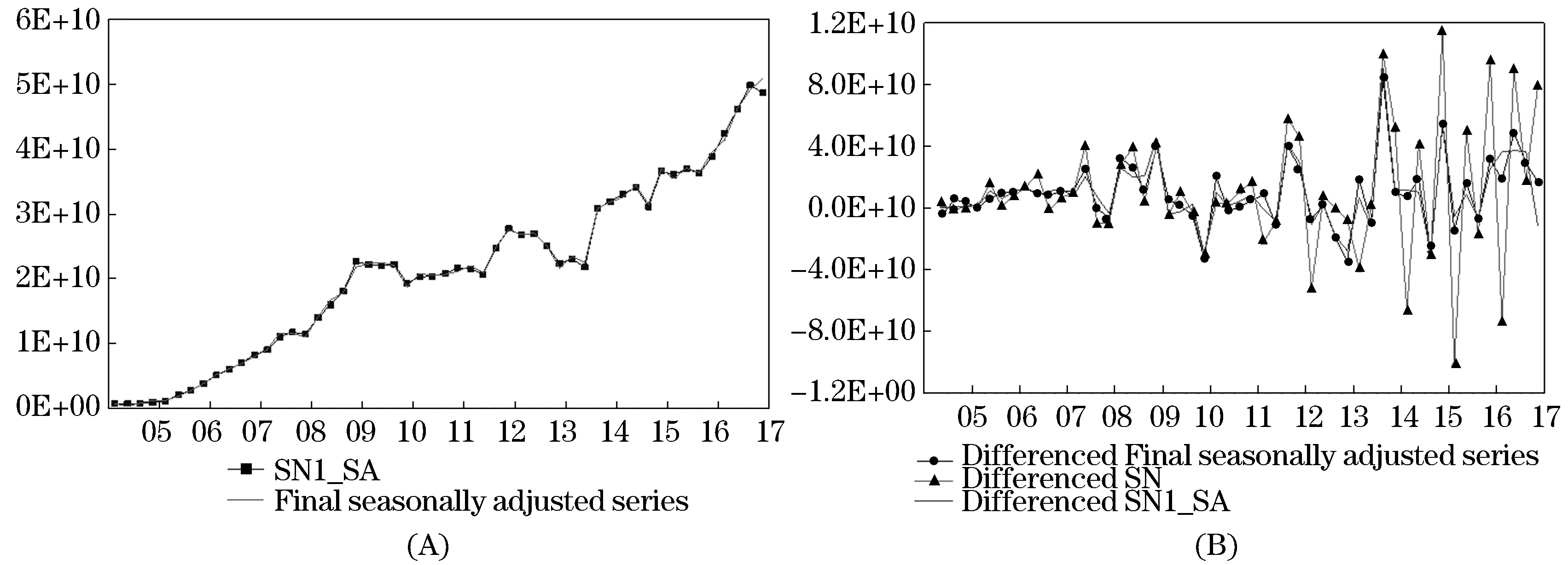
图7 苏宁电器销售量X-12-ARIMA与TRAMO/SEATS季节调整后对比图

以上对苏宁电器销售量序列用X-12-ARIMA和TRAMO/SEATS方法分别进行季节调整，调整后对两次调整的结果对比如图7，图7(A)所示直线为X-12-ARIMA季节调整后的结果，方块线为TRAMO/SEATS季节调整后的结果.如图7(B)所示中三角标识线是原序列、直线为X-12-ARIMA季节调整后差分的结果、圆点标识线为TRAMO/SEATS季节调整差分后的结果，可以看出两种方法处理的苏宁电器销售量数据具有明显的季节特征，变化趋势基本相同，所以两种方法均是可以的.但是观察差分后和差分前的图都会发现TRAMO/SEATS季节调整两端的值缺失比较严重，表现为两头的数据变化较大，中间较小，而X-12-ARIMA季节调整后的值比较完整同时X-12-ARIMA对季节成分、趋势成分的分离比较彻底，所以选用X-12-ARIMA季节调整方法进行以下的研究[14-15].

5 结 语

本文以2005～2017年苏宁电器销售季度数据为例，应用时间序列季节调整X-12-ARIMA和TRAMO/SEATS方法，对比两种季节调整方法，结果显示X-12-ARIMA季节调整方法更适合苏宁电器季度数据.所以选用X-12-ARIMA季节调整方法进行以下模型拟合、估计等研究.