覆盖层厚度对面板堆石坝的动力反应的影响分析

彭雪峰, 朱亚林, 马 驰

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

随着我国经济的发展和西部大开发的实施,水利工程建设正在如火如荼地进行着。其中混凝土面板堆石坝由于拥有良好的安全性、经济性,特别在不良地质条件下所表现出的适应性,使其成为坝工界的首选坝型。由于地形和资源的限制,越来越多的高面板堆石坝直接建在深厚覆盖层上,如坝高为110 m、覆盖层厚度为46 m的新疆察汗乌苏水电站,坝高为112 m、覆盖层厚度为65 m的金川水电站工程,坝高为108 m、覆盖层厚度为100 m的斜卡水电站工程[1]。从文献[2-3]对紫坪铺“5·12”震害的分析，可以发现在地震中,若高土石坝受到破环,则会产生严重的后果,因此对深厚覆盖层上的高土石坝进行动力分析很有必要。

目前,已经有学者在覆盖层厚度对场地的地震反应方面做出了一定的研究。文献[4]利用一维等效线性波动法对单一均质土剖面模型进行了地震反应计算,并通过统计整理所得到的地表加速度值和反应谱平台值后,分析发现,覆盖层厚度对地震波具有放大效应,并且这种放大效应并不是随着覆盖层厚度的增加而持续递增,而是伴随着厚度的增加地震波的加速度峰值有个极大值点。虽然一维等效线性波动法具有概念明确、计算量小的优点[5],但是这种方法无法真实地反映地震波在土体中的传播。此外,文献[6]在进行深厚覆盖层的场地地震反应研究时发现,新建结构的规模越大对覆盖层地震动特性影响也就越大,因此仅以场地为研究对象不足以解决实际工程中的复杂情况。本文参考西部某拟建水利枢纽工程的实际情况[7],通过建立三维模型,对面板堆石坝在不同覆盖层厚度的条件下进行了动力反应分析。

为了能够精确模拟大变形问题和地震波在土体中的传递[8-9],借助基于显示有限差分法的快速拉格朗日数值分析的FLAC3D软件,其优点在于:可以遵循任意指定的非线性本构模型;可以直接计算永久变形等优势。并且根据文献[10],从场地的加速度、坝体的永久变形和防渗体的安全性3个方面分析大坝的地震反应。

1 计算模型及参数

1.1 几何模型

本模型经过简化处理之后,坝高160 m,坝轴线长800 m,坝顶宽度16 m,上下游坡度为1∶1.5,左右两岸坡度比为1∶1,面板厚度按照公式0.3+0.003 5H(H为坝高)取为86 cm,防渗墙厚度为1 m,水位线高度为128 m,覆盖层简化为矩形水平地基。

坝体的三维图如图1所示,一共有31 340个单元和39 402个节点组成。面板、坝体和覆盖层都是由六面体单元和少量的四面体单元组成。在面板和坝体之间,防渗墙的两面均设置了无厚度接触面单元,并在覆盖层的四周加设了自由边界场,采用瑞利阻尼,临界阻尼比为0.05,最小中心频率为5.045 Hz。

图1 三维有限差分网格

1.2 本构模型与材料参数

在使用FLAC3D软件进行计算中,坝体采用常用Mohr-Coulomb弹塑性模型,该模型比较容易模拟出地震时的塑性剪切变形并且直接得到永久位移。计算过程中,堆石料由于受到地震的作用容易发生塑性剪切变形,从而会导致剪切模量G发生变化。为了真实模拟出土石材料的性质,通过自定程序来设定坝体的剪切模量,G的计算公式为:

(1)

其中,pa为标准大气压;σ0为平均应力;C为动剪切模量系数；n为动剪切模量指数。其中C、n通过实验确定[11]。

堆石料的体积模量K可以通过动剪切模量计算得到,当泊松比为0.3时,其K的公式为:

K=13G/6

(2)

坝体在计算过程中涉及到的静、动力计算参数分别见表1、表2所列,其中，1#为主堆石区；2#为次堆石区。

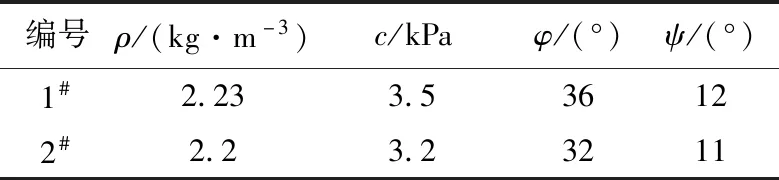
表1 堆石体静力计算参数

注：ψ为膨胀角。

表2 堆石体动力计算参数

分别在面板和土石坝之间、防渗墙和覆盖层之间建立无厚度接触面单元[12],其中由于防渗墙双面临土,需要在其两面都建立接触面,具体参数见表3所列[13],表3中，3#为面板与坝体之间的接触面；4#为防渗墙和覆盖层之间的接触面。

表3 接触面参数

为了突出强调覆盖层厚度单一因子,本文选取均质砂土作为覆盖层材料,其力学参数如下:天然干密度ρd为2.2 g/cm3,变形模量E0为50 MPa,内摩擦角φ为38°。

混凝土面板、防渗墙均采用线弹性模型,分别采用C30、C40混凝土。

1.3 地震时程曲线

本文对某坝址100 a超越频率为2%的基岩期望反应谱曲线进行拟合，得到的人工波如图2所示,其加速度峰值为0.28g。

在计算过程中,在覆盖层底部以顺河道方向输入加速度峰值为0.28g,垂直线方向输入加速度峰值为顺河道方向的2/3,地震总共历时20 s。

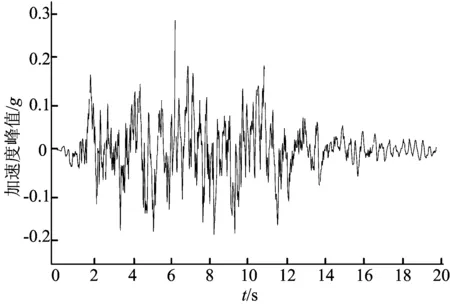
图2 输入地震时程曲线

2 计算结果与分析

为了研究覆盖厚度对大坝的影响,本文将覆盖层厚度划分成10个梯度等级,分别为9、18、27、36、45、54、63、72、81、90 m。对不同覆盖层厚度,分别从场地、坝体和面板3个方面开展了研究。

2.1 场地动力反应分析

加速度放大倍数通常在工程中可以用来描述某种结构对地震动特性的放大作用[14]。首先调整不同加速度峰值的地震波(0.07g、0.21g、0.28g、0.35g)，并从模型底部输入;再选取场地地表四周和中心作为测量点;最后将5个点的加速度反应峰值的平均值除以当前输入地震波的加速度峰值作为场地地表的加速度放大倍数，具体如图3所示。

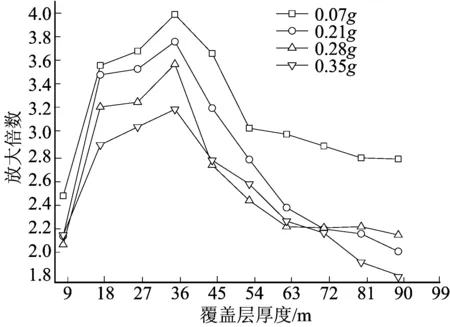
图3 场地加速度放大倍数

从图3可以看出，随着覆盖层厚度的增加,加速度放大倍数呈现先增加后减少的趋势,放大倍数极大值点所对应的覆盖层厚度为36 m;覆盖层对不同地震波的放大效应是不同的,随着地震波加速度峰值增加放大倍数在逐渐减弱;在覆盖层较薄(>36 m)的区域内放大倍数波动较大,而随着覆盖层厚度的增加放大倍数也相继表现出稳定的趋势。由此可见,在不同地震强度下,虽然覆盖层厚度的放大效应存在着差异性,但是极值都对应一个相同的覆盖层厚度,将此厚度称为“临界厚度”,就本案例而言临界厚度为36 m,是大坝高度的0.255倍。该临界厚度还应该与覆盖层的土层材料具有相关性,在实际的工程中应该对该厚度以上的土层进行详尽的重点勘探。

选用加速度峰值为0.28g的地震波作为输入覆盖层底部的动力荷载，分析覆盖层厚度分别为18、36、54、90 m的场地地表的加速度反应谱(阻尼比为5%)，结果如图4所示。

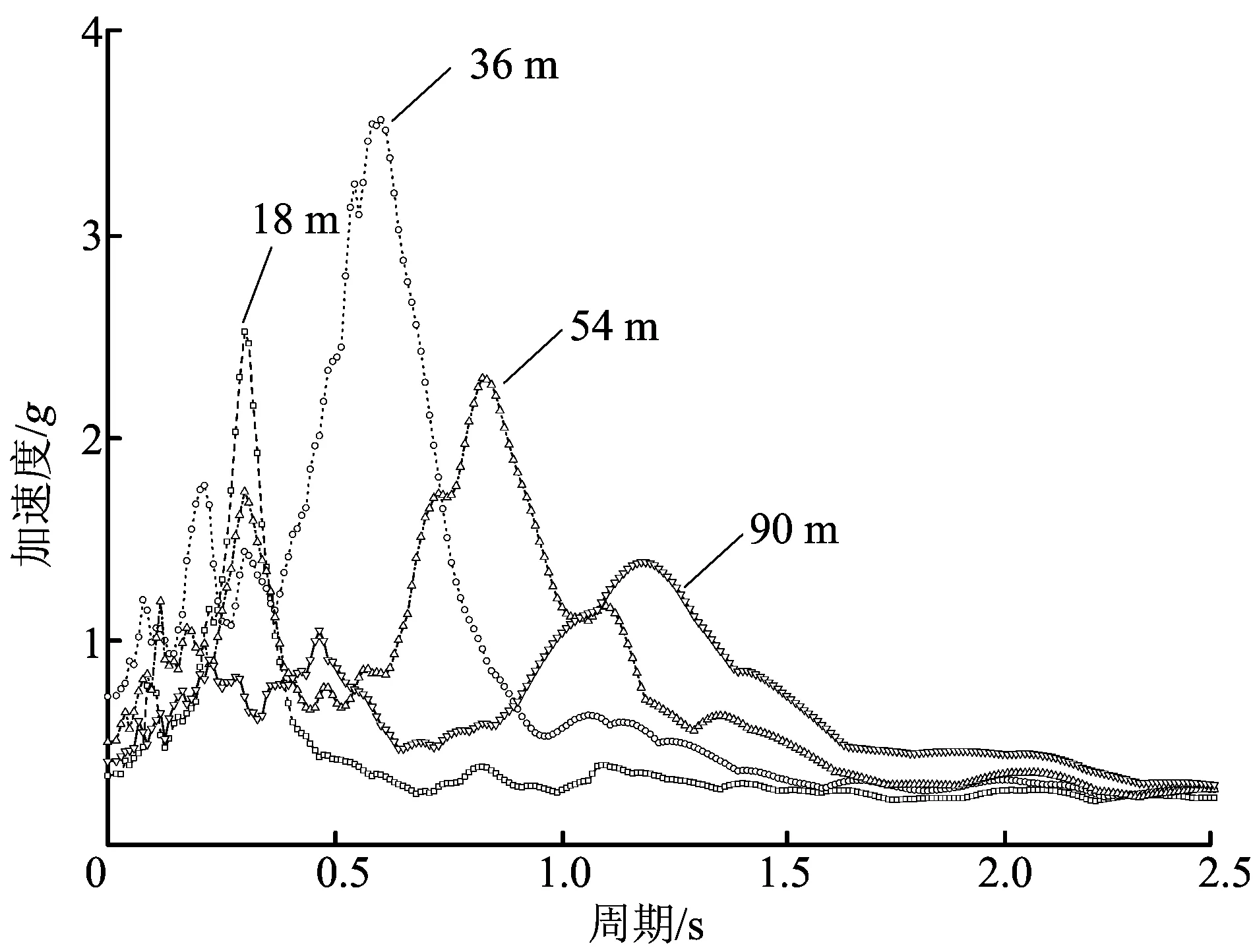
图4 不同厚度的加速度反应谱

由图4可以看出,覆盖层厚度对加速度反应谱的长周期分量的影响较弱,而对短周期分量影响相对明显;伴随着覆盖层厚度的增加,加速度反应谱出现向长周期方向“走移”的现象。

2.2 坝体位移反应分析

坝体边坡的稳定状态可以从坝体的特定位置上的永久位移来反映,当坝体内不断累积的永久变形到达一定的程度就可能导致坝体发生失稳破坏。因此在实际工程中坝体的永久变形是作为高土坝抗震能力的一个重要指标[14]。

不同覆盖层厚度9～90 m的坝体下游中轴线上(Y轴为0)顺河道方向和垂直方向的位移如图5所示。

图5 不同覆盖层厚度顺河道方向和垂直方向位移分布

从图5可以看出,由于“鞭鞘效应”,水平位移和垂直在坝体的上半部分出现了明显的转折,位移的最大值出现在了坝高9/10的位置;随着覆盖层厚度的增加,下游坡面2个方向的位移先增加后降低,并且当覆盖层厚度为临界厚度(36 m)时,下游坡面的位移出现了最大值,这与一开始假设的临界厚度(36 m)的值是一致的。

2.3 面板动力反应分析

文献[15]在对高面板堆石坝面板应力分布特性做分析时发现,震后面板的坝轴向(Y轴)应力对面板安全威胁是比较大的,本文仅对面板震后坝轴向应力进行分析。

面板震后主要受到的是压应力(负值)。由于地震结束之后,坝体的永久位移向着下游侧倾斜,导致在坝段的中部面板的上部(接近坝顶)出现大范围的挤压应力;而拉应力(正值)主要是分布在面板与河谷两岸交接并且靠近坝顶的地方。覆盖层厚度从9～90 m的混凝土面板坝轴向相应的最大拉压应力如图6所示。从图6可以看出，面板受到压应力和拉应力都出现在覆盖层厚度为27 m的位置,其值分别为18.42、0.572 MPa。

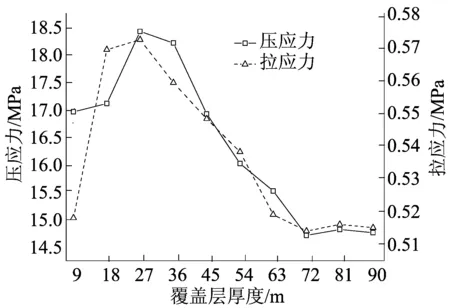
图6 覆盖层厚度的面板沿坝轴向应力

面板的拉、压应力极大值和加速度放大倍数极值、永久位移极值所对应的覆盖层厚度见表4所列。

由于地震波传播的介质均为覆盖层的岩土材料,坝体的加速度放大倍数极值、顺河道位移、垂直向永久位移极值所对应的覆盖层厚度都为36 m。而当地震波经过防渗墙的传播,波速相比于在岩土材料中传播发生了变化,与防渗墙相接的面板的拉压应力极值所对应的覆盖层厚也发生了改变，为27 m。这表明当传播地震荷载的介质改变会导致临界厚度的变化。

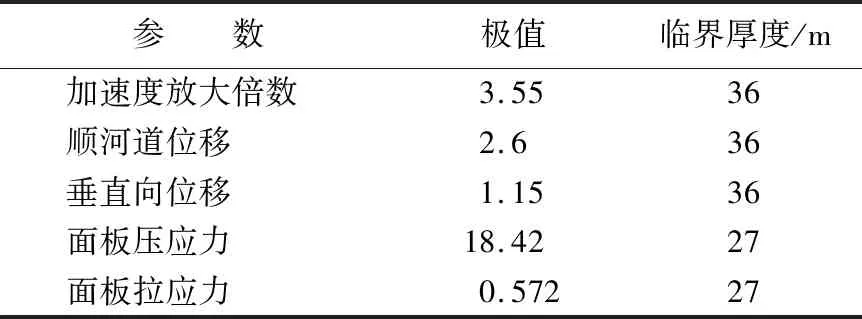
表4 临界厚度的变化

注：顺河道位移、垂直向位移极值单位为m；面板拉、压应力极值单位为MPa。

3 结 论

本文基于西部某拟建面板堆石坝资料建立三维坝体模型,并进行了在深厚覆盖层上坝体的动力计算,主要分析计算了覆盖层土层的厚度对场地、坝体以及面板的动力反应的影响,得出的主要结论如下:

(1) 覆盖层的存在会对输入地震波的动特性产生影响,使得场地地表的加速度振幅有所增加,整体呈现先增加后减小的趋势,存在一个“临界厚度”,应该对此厚度以上的地质情况做详尽的勘查。

(2) 从场地地表加速度反应谱中可以得到,随着覆盖层厚度的增加,反应谱出现向长周期方向“走移”,卓越周期在逐渐增大,在实际工程中,需要参考规范，结合不同的覆盖层厚度选取合理的场地特征周期。

(3) 当覆盖层处于临界厚度时,坝体的整体位移无论是在数值上还是大位移的范围上都处于最大值,需要在有效增加抗震设施的同时扩大抗震范围。

(4) 从不同覆盖层厚度的面板拉压应力折线图可以看出,由于防渗墙与覆盖层土体的材料差异性,导致面板应力极大值所对应的临界厚度有所降低。

覆盖层地基的条件不同对混凝土面板堆石坝的动力反应会产生巨大的影响,本文仅仅考虑了覆盖层厚度单一的因素,然而覆盖层纵向截面的形状和覆盖层的土层地质条件对面板堆石坝的动力反应也会产生一定影响,在后续的研究中会侧重在这2个方面。