数据分布可变的股市拐点预测方法

姚宏亮, 施振振, 王 浩

(合肥工业大学 计算机与信息学院 安徽 合肥 230601)

股市是一个复杂的非线性动态系统[1],是众多因素共同作用的结果,受到政策、社会新闻事件、公司本身经营状况以及投资者心理变化等众多因素的影响[2-3],因而股市趋势预测是机器学习中具有挑战性的研究问题。同时,拐点预测是股市趋势中的关键性难题[4]。

近年来,不少研究者利用支持向量机(support vector machine,SVM)预测股市的拐点。文献[5]提出了成交量加权支持向量机(volume weighted SVM,VW-SVM)模型对股市拐点进行预测;文献[6]针对传统加权支持向量机(weighted SVM,W-SVM)中参数需要人为指定的问题,提出了融合遗传算法的加权支持向量机(genetic algorithm weighted SVM,GAW-SVM)模型,对股票拐点进行预测; 文献[7]根据拐点变化幅度对拐点赋予不同的权值,用分段线性表示(piecewise linear representation,PLR)方法对股票趋势进行预测。

股市受到实时因素的影响,且这些因素具有不确定性[8-9],因而股票趋势数据的分布具有可变性。传统方法利用较长时间的历史数据学习模型,忽略数据分布可变性,难以有效预测股市拐点[10]。文献[11]提出用滑动窗口方法来处理数据分布变化,但仅考虑近期数据分布,容易产生过拟合,导致模型的适应性不佳。

本文将用历史数据学习得到的模型和用近期数据学习得到的模型进行融合,通过引入平衡项,提出一种平衡加权支持向量机(balance weighted SVM,BW-SVM)模型。BW-SVM模型对历史数据分布和近期局部数据分布进行了融合,其中平衡项是用历史数据学习得到结果和用近期局部数据学习所得结果的均方误差,其中误差项可以通过调节系数μ进行调节。

拐点相关的特征提取,是有效发现拐点的重要基础[12]。目前研究者一般从传统技术指标中提取与股市拐点相关的特征[13],这些特征能在一定程度上体现近期数据分布的变化。本文在传统技术指标基础上,通过对指标进一步量化得到拐点的能量特征,然后利用马尔可夫毯对提出的特征进行融合,最后将能量特征带入BW-SVM模型,对股市拐点进行预测。

本文先给出BW-SVM模型的形式化表示,推导出BW-SVM模型的分类函数;然后提取具有能量信息的特征,利用马尔可夫毯对拐点的能量特征进行融合,得到能量特征与拐点之间的结构关系;再将能量特征带入BW-SVM模型得到基于能量的平衡加权支持向量机(BW-SVM based on energy,EBW-SVM)算法,并用遗传算法对模型参数进行优化;最后通过真实数据集上的实验结果验证了算法的有效性。

1 BW-SVM模型

1.1 W-SVM模型

W-SVM模型的分类函数为:

f(x)=w·φ(x)+b

(1)

其中,φ为未知函数。最优化问题可表示为:

s.t.yi[(w·φ(xi))+b]≥1-ξi，

ξi≥0,i=1,2,…,n

(2)

其中,C为惩罚参数,C>0;si为权重;ξi为松弛变量;n为样本个数;xi为训练数据。

1.2 BW-SVM模型

在W-SVM模型上,在目标函数中增加平衡项μ‖wt-ws‖2,其中,μ为调节系数,ws为使用较长时期的历史数据学习得到的模型参数,wt为用近期数据学习得到的模型参数(本文取最近20个交易日的数据),得到的BW-SVM模型表示如下:

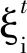
(3)

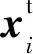
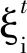
(4)

进而,可得到展开式的对偶形式为:

(5)

其中,ns为历史数据样本数;αs为根据历史数据训练得到的模型对偶形式的解。利用Matlab中的quadprog函数求解该对偶形式的解αt,可得:

(6)

(7)

wt、bt为BW-SVM分类函数的系数和常数项,代入(1)式,得到分类函数:

f(x)=wt·φ(x)+bt=

(8)

其中,K为给定的核函数。

2 EBW-SVM算法

2.1 能量特征提取

从多空角度来看,股市的波动是能量作用的结果,而拐点的产生是能量从一种趋势变成另一种趋势造成的。传统技术指标如KDJ指标、异同移动平均线(Moving Average Convergence and Divergence,MACD)指标等也具有能量分布特性,但只是能量变化的一种基本表示,与实际能量波动存在较大的不一致性。本文对传统技术特征进一步量化,以提取更有价值的特征。

2.1.1 KDJ指标的能量特征

KDJ指标由K线、D线和J线构成,表示最高价、最低价及收盘价之间的关系,被广泛用于金融市场中短期的趋势分析。当i时刻K线向上时,即ΔKi=(Ki-Ki-1)/Ki-1>0,向上趋势的能量强度可以用|Ki-Di|表示,其加权能量强度可以表示为|Ki-Di|ΔKi,K线的变化幅度越大,其加权后的能量越大;若ΔKi<0,则当前是下跌趋势,对应的能量值为负。

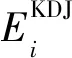
(9)

2.1.2 影线比重的能量特征

影线比重的能量特征为:

(10)

其中,Oi、Hi、Li、Ci分别为i时刻股票的开盘价、最高价、最低价及收盘价;ξ是为了防止分母为0的偏置值,这里取ξ=0.000 1。上下影线长度与上方压力或下方支撑力有关。

2.1.3 移动平均线指标的能量特征

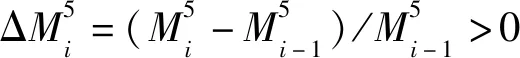
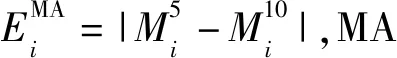
(11)

2.1.4 相对强弱指标的能量特征

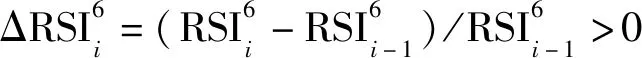
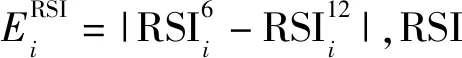
(12)

2.1.5 成交量移动平均指标的能量特征

(13)

2.1.6 当前价格所处位置的能量特征

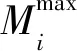
(14)

图1 股票600031当前价格所处的位置

2.1.7MACD的能量特征

MACD是利用收盘价的短期(常用12日)指数移动平均线与长期(常用26日)指数移动平均线表示趋势的变化情况,由离差(difference,DIFF)线、离差值的指数平滑移动平均(difference exponential average,DEA)线和MACD能量柱组成。当DIFF线向上,即ΔDIFFi=(DIFFi-DIFFi-1)/DIFFi-1>0时,当前趋势向上,向上的能量强度可以用|DIFFi-DEAi|表示,此时加权能量强度可以表示为|DIFFi-DEAi|ΔDIFFi,DIFF的变化幅度越大,其加权后的能量越大;若ΔDIFFi<0,则当前是下跌趋势,对应的能量值为负。

(15)

2.2 拐点的马尔可夫毯

利用马尔可夫毯对能量特征进行融合,得到能量特征与拐点之间的结构关系。将上述能量特征进行离散化,并利用K2算法构建贝叶斯网络,如图2所示。

图2中,1～7号节点分别代表T1～T7指标,8号节点为拐点。

对于一个变量T和变量子集S,T∉S,给定T的马尔科夫毯(记作MB(T)),若变量T与贝叶斯网络中的其他变量间是条件独立的,即存在I(S,T|MB(T)),称MB(T)为最小特征子集[14]。MB(T)包含了变量T的所有信息,且这些信息无法从变量集的其他变量中得到[15]。在贝叶斯网络图中,MB(T)是由变量T的父结点、子结点和子结点的父结点组成的[16]。

图2 拐点的贝叶斯网络

由图2可知,8号拐点的父节点为1、2,子节点为5、6、7,子节点的父节点为1、2、3、5,其马尔科夫毯如图3所示。

设TP(turning point)为拐点信息,马尔科夫毯对拐点相关特征融合后的能量用ETP表示,其条件概率函数为:

PTP=P(ETP|T1,T2,T3,T4,T5,T6,T7)

(16)

图3 拐点的马尔科夫毯

2.3 EBW-SVM算法步骤

输入:股票日线数据集Dateset。

输出: 拐点。

(1) 根据(9)～(15)式,从Dateset中提取7个能量特征T1～T7及真实拐点标签,并将数据分为训练集、验证集及测试集。

(2) 利用马尔可夫毯对能量特征进行融合,并得到融合后的能量函数。

(3) 将训练集特征带入W-SVM模型进行训练,得到W-SVM的模型参数ws。

(4) 基于ws,提取测试集的前N个交易日为局部训练集,带入EBW-SVM模型进行训练,得到EBW-SVM模型。

(5) 利用EBW-SVM模型对拐点进行预测。

2.4 模型参数优化

根据(3)式,EBW-SVM模型中有5个参数

需要事先设定,分别是惩罚因子C、调节系数μ、拐点的权重s1、非拐点的权重s2,以及径向基函数(radial basis function,RBF)的参数γ。一般地,高维特征选择线性核函数,低维特征选择RBF核函数[17],因此选择RBF核函数。RBF核函数为:

K(x,xi)=exp(-γ‖x-xi‖2)

(17)

这里用遗传算法(genetic algorithm,GA)对模型参数进行全局寻优,5个参数的寻优范围如下：C取值为0～1 000;s1取值为0.01～1;s2取值为0.01～1;μ取值为0～10;γ取值为0.000 1～10。

将历史数据分成训练集和验证集,GA算法的目标是最大化验证集的F1值(以下简称F1)。F1是一种常用的衡量分类效果好坏的指标,其计算公式为:

(18)

其中,Ravg为平均召回率;Pavg为平均准确率。

3 实验比较与分析

为了验证取不同局部数据对实验结果的影响,分别取N为前20、50、100、200、500个交易日,并从准确率、召回率及F1值3个方面和文献[6]提出的算法进行比较,结果见表1～表3所列。

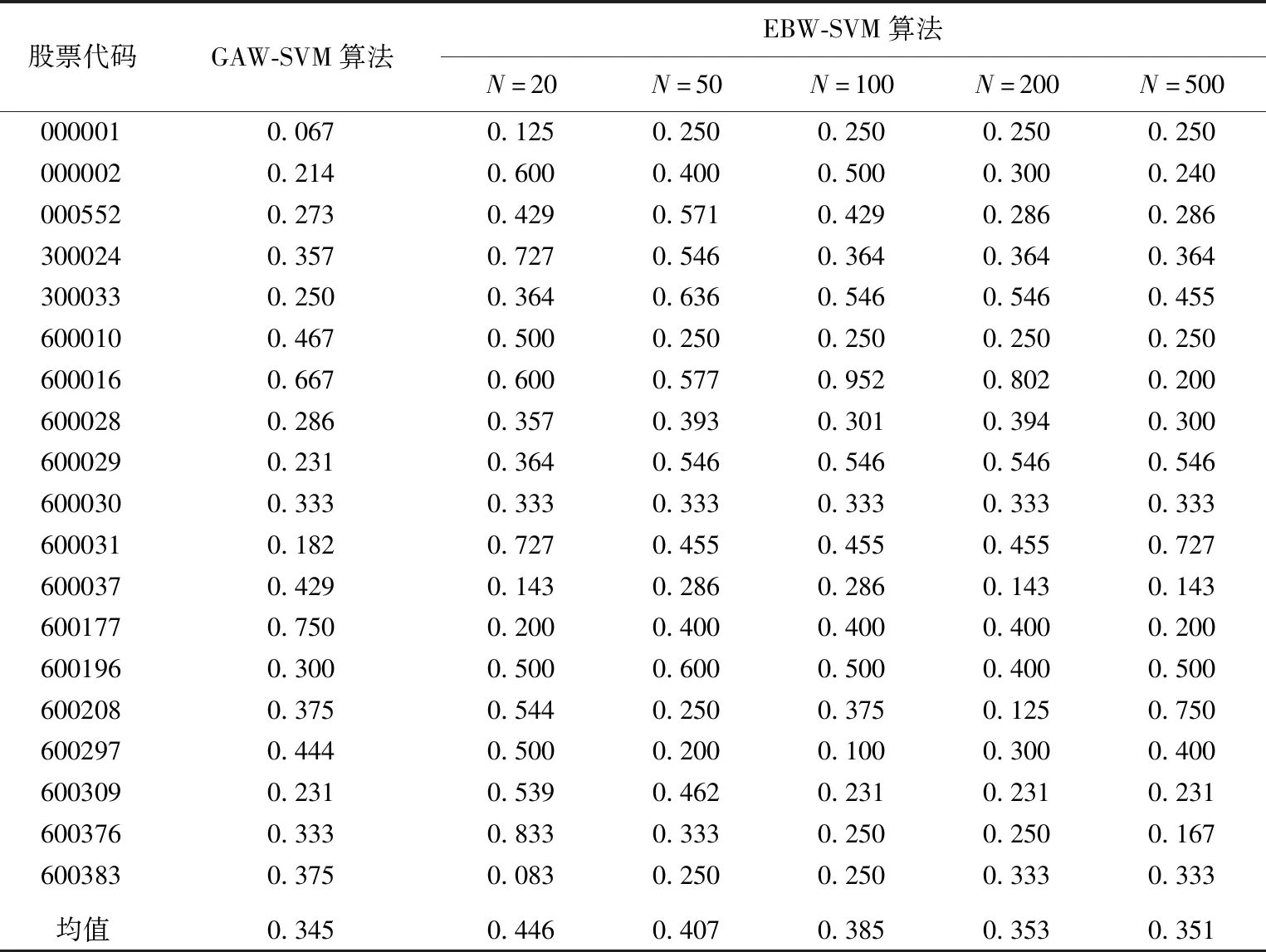
表1 GAW-SVM算法和EBW-SVM算法准确率对比

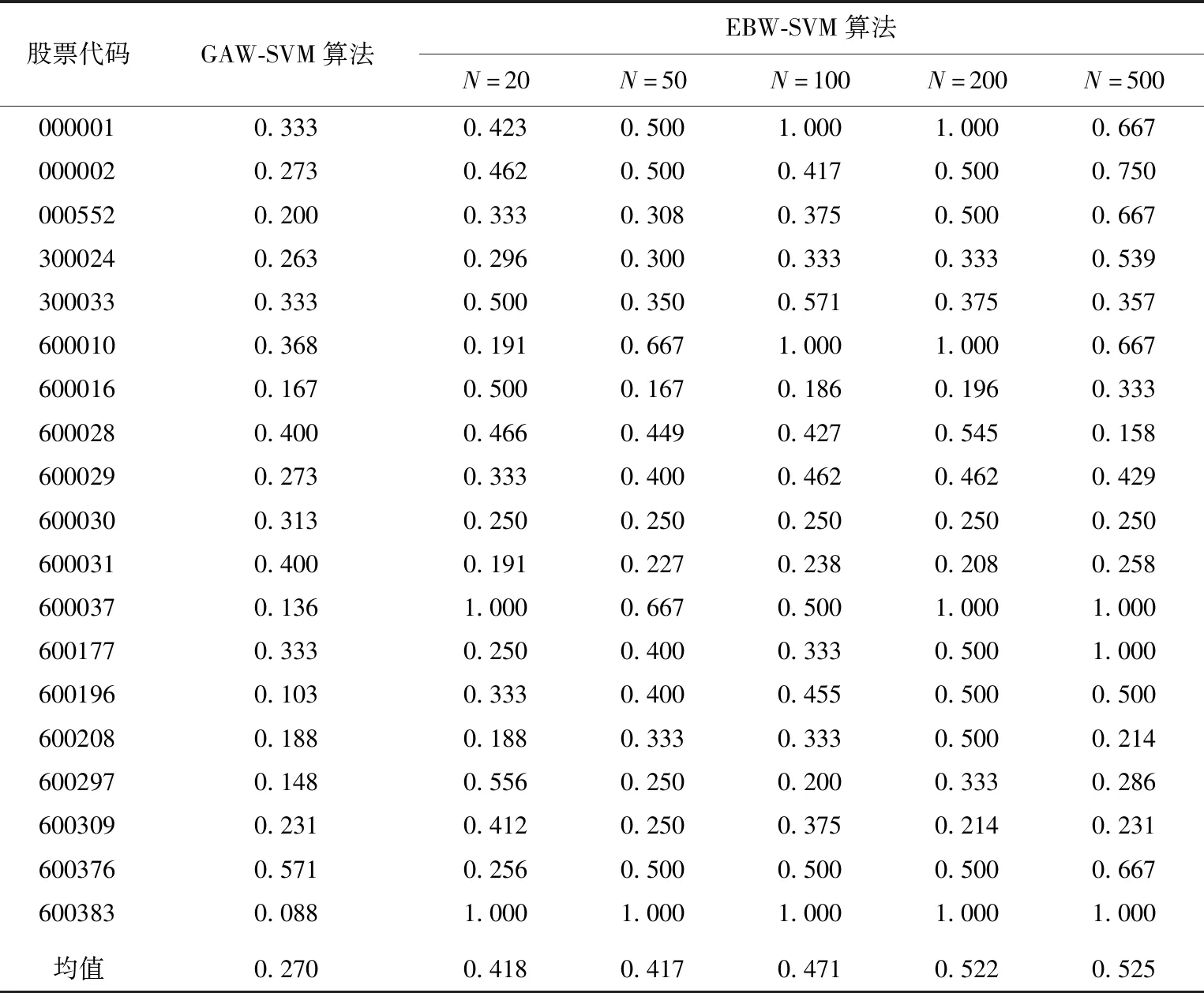
表2 GAW-SVM算法和EBW-SVM算法召回率对比

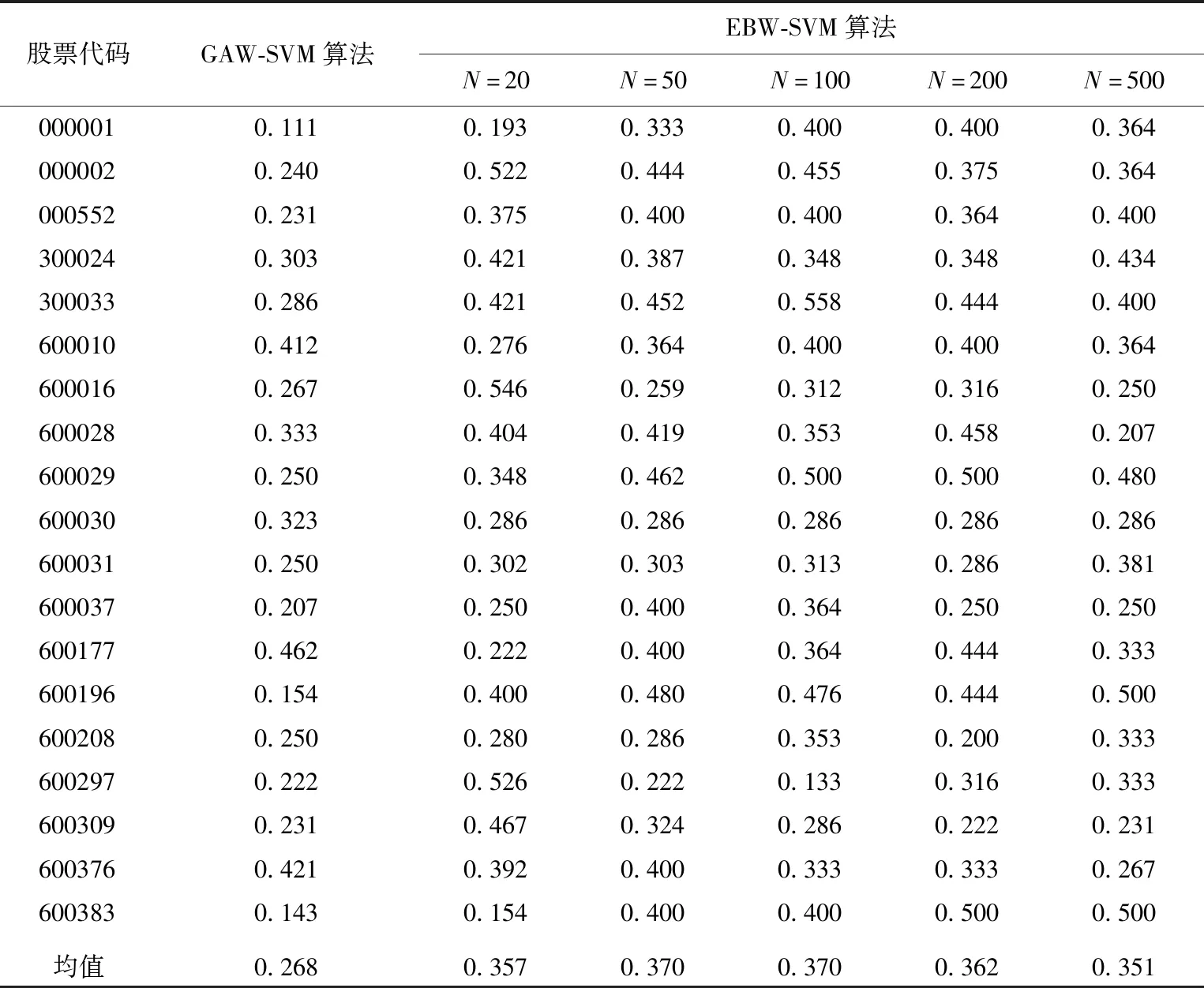
表3 GAW-SVM算法和EBW-SVM算法F1值对比

从表1～表3可以看出,当N取不同值时,EBW-SVM算法的表现均比GAW-SVM算法好。在准确率方面,N为20或50时EBW-SVM算法的表现最好,N为100时次之,N为200或500时最差。在召回率方面,当N为200或500时EBW-SVM算法的表现最好,N为100时次之,N为20或50时表现最差。F1值,当N为100时EBW-SVM算法的表现最好。

由此可知,N太小时EBW-SVM算法容易对拐点过于敏感,而N太大又过于保守,选择适当的局部数据进行第2次训练,有助于整体预测效果的提升。

4 结 论

本文主要针对目前历史数据学习模型的方法忽略近期数据分布变化,导致拐点难以有效发现的问题,提出一种融合能量特征的支持向量机股市拐点预测方法(EBW-SVM)。在原W-SVM模型中引入平衡项得到BW-SVM模型,然后在能体现数据分布变化的技术指标基础上,进一步量化提取拐点的能量特征,并利用马尔可夫毯融合拐点的能量特征,最后将能量特征带入BW-SVM模型对股市拐点进行预测。实验分析结果表明,EBW-SVM算法具有良好的性能。