喷流制冷的高超声速后台阶流场气动光学效应研究*

邢博阳,杨俊彦,余 跃,张 斌

(1.上海交通大学 航空航天学院·上海·200240;2.上海航天控制技术研究所·上海·201109)

0 引 言

临近空间通常是指海拔从20km到100km不等的区域,近年来其已成为世界军事强国的重要研究方向。临近空间的空气密度很小,并且随高度呈指数下降趋势[1]。例如,当海拔为40km时,空气密度约为海平面标准密度的1/300;当海拔为60km时,空气密度约为海平面标准密度的1/4000;当海拔为80km时,空气密度接近真空。近几十年来,许多学者通过实验或数值模拟研究了后台阶的特征,并发现了流场中的一些典型结构,如膨胀波、剪切层、回流区、重新附着点,以及重新附着冲击等[2-5]。朱杨柱[6]发现,随着马赫数的增加,再附着点位置逐渐向后移动。陈植[7]通过实验获得了马赫数为3的超音速层流和后台阶湍流结构,结果表明回流区的长度约为台阶高度的7.5倍。Eaton[8]回顾了亚音速湍流后台阶的再附着点,并指出回流区的长度在6~8倍的台阶高度之间。工程中出现的后台阶构型的流场通常伴随着喷流制冷现象,目前也有大量针对喷流冷却的后台阶流场研究。张锋[9]采用基于纳米粒子的平面激光散射技术对不同静压比下马赫数为3的超声速冷却气膜流场进行了实验研究。结果表明,在波系结构、喷流厚度及湍流化程度等方面,静压比对超声速冷却气膜产生了显著的影响。朱志斌[10]以光学窗口外冷喷流为研究背景,采用大涡模拟方法对后台阶外形切向喷流混合流场进行了研究,获得了流场结构特征、时空演化规律及流场密度脉动特性。邓放[11]采用高精度格式求解了二维Navier-Stokes方程,研究了超声速射流与同向超声速后台阶流动相互作用的流场基本结构及规律,讨论和分析了流场中复杂的波系结构及其相互干扰的流动现象。

如上所述,已有大量文献对亚音速和超音速的后台阶流场进行了实验和数值研究。但是,临近空间的高超音速流动很少受到关注。在超音速和高超音速飞行器的光学头罩中,通常会出现向后台阶结构,研究近空间高超声速后台阶的流场对于工程应用而言具有重要意义。

具体而言,本文既关注不同喷流冷却形式的冷却效果,又关注相应条件下流场的气动光学效应。文章使用由课题组开发并已通过验证[12-14]的高精度直接模拟蒙特卡洛算法(Direct Simulation Monte Carlo,DSMC)[15]计算临近空间高超声速的后台阶流场。此外,提出了一种基于计算网格和直接仿真的光线追踪技术,用于计算气动光学效应。结果表明,临近空间高超声速后台阶流场在高度大于30km时可忽略不计。本文同时比较了四种喷流冷却方式的制冷效果和气动光学效应。

1 数值方法

1.1 DSMC方法

本文采用DSMC方法计算不同条件下的后台阶流场。DSMC是一种基于Boltzmann方程的数值模拟方法,采用大量分子模型模拟物理分子的真实运动,以计算宏观物理量,如速度、温度、密度、压力、质量等。DSMC方法能够准确地模拟从自由分子流动区域到接近连续流动区域的大多数空气动力学问题,是解决稀薄气体区域和过渡区域中的空气动力学问题的唯一成功的数值方法[16]。分子碰撞过程的模拟基于可变硬球模型(Variable Hard Sphere,VHS),化学反应采用量子-动理学(Quantum-Kinetic,Q-K)模型,采用自适应子网格技术满足碰撞要求,采用变时间步长、metis负载平衡分区等加速技巧提高程序的计算效率。本程序能够模拟超声速、高超声速的单一组分气体和多组分混合气体,并可考虑高温空气离解的可压黏性流动,尤其在稀薄领域具有明显优势。DSMC方法的工作过程可以概括为如下步骤:

(1)读取网格数据,记录边界条件信息;

(2)初始化流场,计算实际分子的进入数量;

(3)模拟分子运动,并与边界相互作用;

(4)索引所有模拟分子;

(5)按概率选择模拟分子,并发生碰撞;

(6)对单元和壁面信息进行采样,并重复3~6次,使其稳定;

(7)输出流场和壁面信息。

1.2 光线追踪方法

为研究光束穿过混合层流场的气动光学效应,本文采用了基于流场网格和直接模拟的光线追踪技术。这种方法基于光沿着直线传播的假设,可以通过光线追踪模拟光粒子在非均匀介质中的运动轨迹,进而得到一系列的气动光学评价参数。

粒子在穿越网格时,折射或反射现象均有可能出现,如图1所示。粒子的反射或折射现象与粒子是从光密介质进入光疏介质还是从光疏介质进入光密介质有关。具体而言,粒子的反射或折射取决于粒子历经的相邻两个网格的折射率大小。

图1 二维光线追踪示意图Fig.1 The ray tracing method in 2D plane

图2所示的光线追踪流程可概述为以下几个步骤:(1)初始化计算,在边界上布置虚拟光粒子;(2)在给定时间步长内根据牛顿定律迁移粒子;(3)确定粒子是否离开原始网格。如是,转至(4),否则继续迁移;(4)确定粒子是否穿越了计算域边界,如是,停止,否则计算网格面编号及穿越的位置;(5)根据折射率更新粒子速度,并继续迁移粒子。

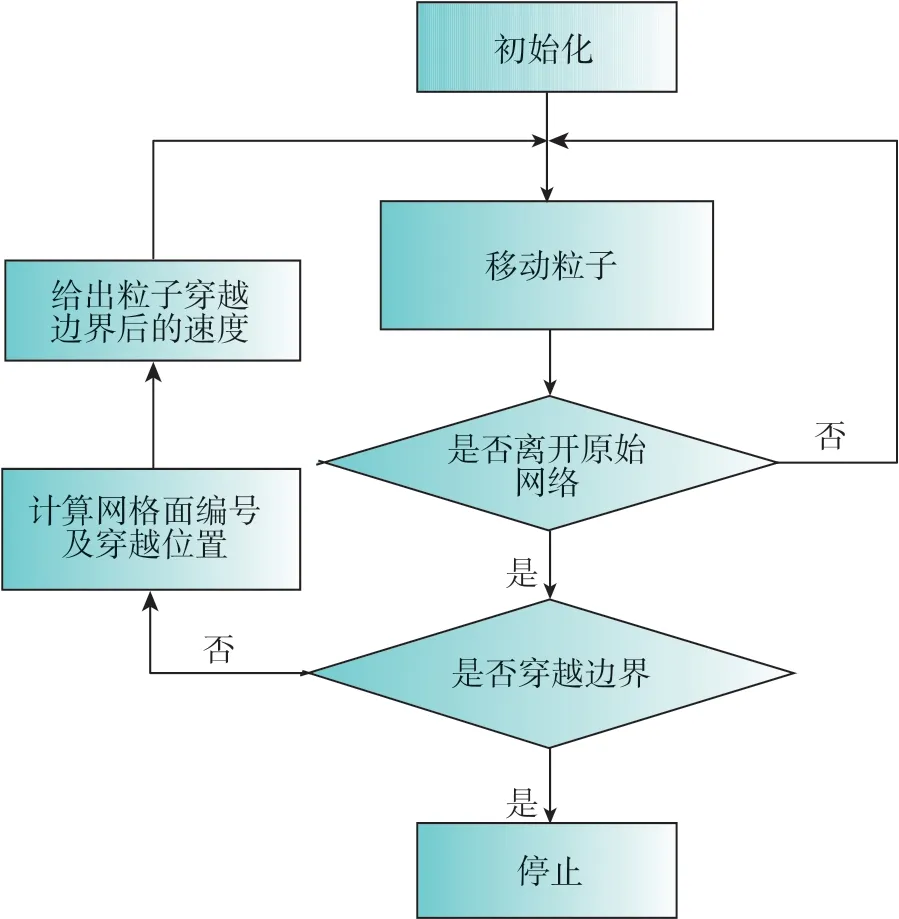
图2 光线追踪流程图Fig.2 The computational procedure of ray tracing method

粒子在穿越整个计算流场后,沿其经历的路径可以得到该粒子的光程(Optical Path Length,OPL),计算公式如式(1)所示。其中,c为光线积分路径,n是光线所通过每一个网格的折射率,由网格内密度换算而来。

光程差(Optical Path Difference,OPD)同样是光学评价中的重要参数,由式(2)得到,其中尖括号表示空间平均。

2 算例设置和网格无关性验证

2.1 网格模型

后台阶结构流场(Backward-Facing Step,BFS)具有展向中心对称的特点,并且展向宽度与台阶高度足够大,因此本文中的流场模拟可以采用二维模型进行计算,流场计算区域如图3所示。后台阶上下游壁面互相平行,后台阶高度h为5mm,上游壁面和台阶下游壁面的长度分别为60mm和100mm。流场上游的流场宽度为40mm,下游流场宽度为45mm。

图3 后台阶流场示意图及CFD计算区域Fig.3 Schematic diagram of the BFS and the computational area of CFD

对于喷流介质的选取,从容易获得且价格低廉等角度考虑,选取氮气作为喷流介质。垂直喷流出口设置在距离后台阶上游9mm位置处,喷缝沿着展向设置,宽度为2mm。喷流速度马赫数为1。另外,沿着后台阶竖直立面距离上壁面2mm处设置喷缝宽度为2mm的水平喷流出口,喷流速度马赫数为3。所有喷口均为方形。

2.2 算例设置

本文的主要目的是研究临近空间范围内的后台阶流动问题。临近空间范围为20km~80km,文章中主要讨论的计算范围为30km~60km,后台阶流动不同喷流控制的算例以30km流场作为基准。分别采用A、B、C、D四种不同的喷流方式,研究不同喷流方式对后台阶流动控制的影响。

对于后台阶流场,左侧和右侧边界是自由流边界条件,上下游下方边界是等温壁面条件,壁面条件为无滑移等温壁面。给定壁面温度为400K,喷流温度为300K,不同位置的喷流可以起到冷却作用。对于所有的算例,来流条件为马赫数6。来流空气组分为78%的氮气(N2)和22%的氧气(O2),空气的摩尔分子质量为28.96(kg/mol),比热比为1.4。其他详细参数(如静压、静温等参数)如表1所示。其中,H表示飞行高度,P0表示来流压强,T0表示来流气体温度,U0表示远场来流速度,Ma表示马赫数。

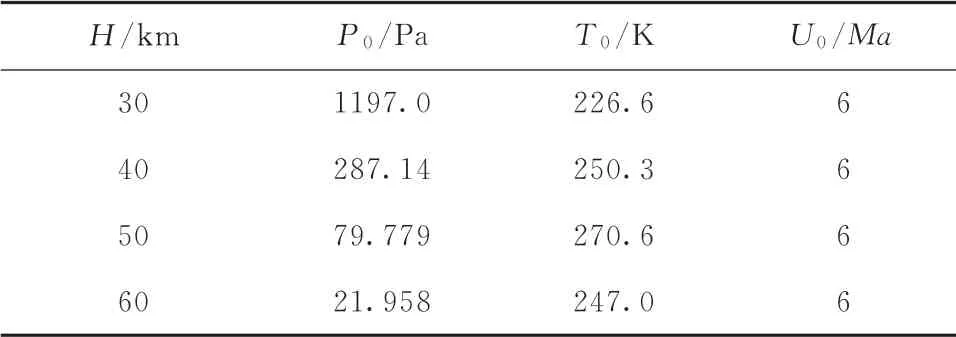
表1 不同高度后台阶流场计算条件Tab.1 Boundary conditions for the basic BFS flowfield

不同喷流控制流场的角度设置如图4所示。喷流方式A、B的喷口在竖直立面,喷流方式A的喷流方向为沿水平方向,喷流方式B的方向为斜向上45°。喷流方式C、D的喷口位置在上游壁面上,喷流方式C的方向为竖直向上,喷流方式D的方向为斜向上45°。不同喷流参数(如静压、静温等参数)的设置如表2所示。其中,Pj表示喷流介质的压强,Tj表示喷流气体的温度,Uj表示冷却喷流的速度。

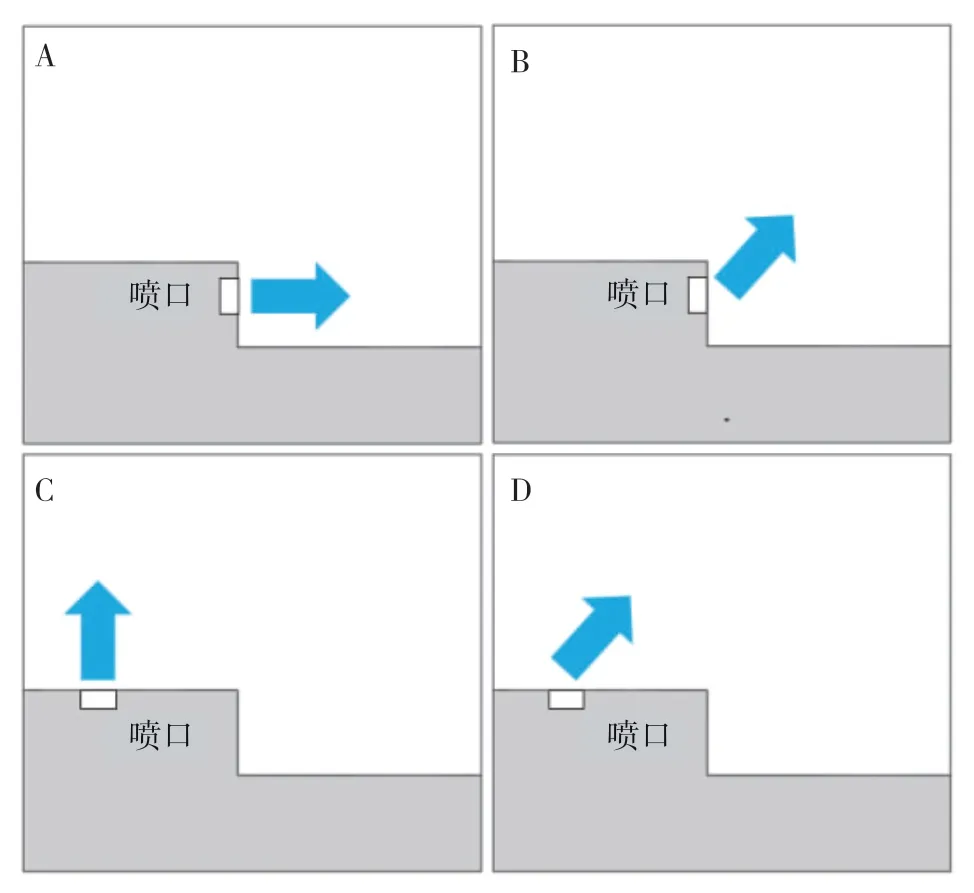
图4 不同喷流方式示意图Fig.4 Schematic diagram of different film cooling modes

表2 不同喷流方式的喷流计算条件Tab.2 Computational conditions for the BFS of different film cooling modes

2.3 网格无关性验证

DSMC方法是直接求解Boltzman方程的方法,采用模拟流体粒子运动的方式对流场进行仿真。DSMC方法对网格尺寸和采样粒子的数量均有较高的要求,因此要对后台阶流场问题进行网格无关性验证。坐标系建立在后台阶拐角处,x、y两个方向分别为流向和竖直方向。

本文采用81121网格、202521网格和401501网格三种不同加密程度的网格进行计算。网格如图5所示,其中横纵坐标分别表示为x/h、y/h,h为无量纲化的后台阶高度。

图5 后台阶流场计算网格Fig.5 Computational grid for 2D BFS

网格密度沿着后台阶壁面加密,接近壁面的网格尺度为20μm。应用DSMC方法计算后台阶流场需使用三种不同尺寸的网格。后台阶流场的高度为30km,x/h=5处的纵向截面速度分布和温度分布如图6所示。由图6可以看出,三套网格数值仿真结果中的速度和温度没有明显的差异。放大来看,中等网格和加密网格的结果更加接近,因此可以采用中等网格或加密网格进行流场模拟计算。为了减少计算量,下文所有数值仿真均采用中等加密的网格进行计算。

3 结果与讨论

3.1 不同飞行高度后台阶流动特征

首先研究无喷流后台阶流场在30km~60km的流动特征,以下计算结果均是DSMC算法的时均结果。图7是不同高度下后台阶流场的密度云图。从图7可以明显看出,随着飞行高度增加,流场密度不断降低。高度越高,空气越稀薄,这是由大气密度随高度变化本身决定的。可以看到,在高度为30km、40km时,流场存在明显的前缘激波、后台阶回流区、在附着激波等流场结构。同时可以看到,随着高度增加,流场压缩性减小,前缘激波角度减小,并且后台阶回流区的大小也随着飞行高度的增加而不断减小。当高度为50km、60km时,流场更加稀薄,导致在附着激波也不再明显。从显示流场的流线可以看到,激波角度的增大使得流动速度方向向上抬升了微小的角度。

图6 三种网格在X/h=5处的流向速度(左)和温度(右)的网格无关性验证Fig.6 Comparison of stream wise velocity(left)and temperature(right)along the vertical line ofX/h=5 for three different grid densities

图7 不同飞行高度后台阶流场的密度云图和流线Fig.7 The density contour with streamlines for the cases of basic BFS at different altitudes

通过DSMC仿真流场可以得到后台阶下游壁面的热流系数CQ,如图8所示。由图8可以看到,在高度为30km、40km时,后台阶下游壁面的热流系数在回流区右边界处出现热流系数峰值。在高度为50km、60km时,后台阶流场的来流密度出现了显著降低,热流系数在下游壁面持续增加。总体而言,随着飞行高度的增加,后台阶流场下游壁面的气动热问题愈发严重。

3.2 不同喷流方式后台阶流动特征

采用DSMC方法计算不同喷流方式的流场(来流均为Ma=6),可以得到流场的密度云图,如图9所示。从图9可以看到,对于A、B两种平行于壁面的冷却喷流方式,喷流方式A的回流区偏小,喷流出口的流线沿着喷口向两边略微膨胀。喷流经过回流区沿着壁面向下游流动,对壁面起到了冷却作用。

图8 不同高度下后台阶流场的热流系数Fig.8 CQ for BFS at different altitude

对于喷流方式B,由于喷流方向为斜向上45°,喷流下方的回流区相比喷流方式A略微增大。同样,喷流在越过回流区后贴近下游壁面,可对流动起到冷却作用,同时与上游自然来流形成剪切层。

对于喷流方式C,喷口设置在距离后台阶竖立面边缘9mm的位置,垂直喷流与来流形成了典型的喷流结构。可以看到,竖立面左侧流场中有分离区,喷口两侧有回流区、马赫盘、膨胀激波等复杂的流场结构。自由来流在遇到喷流形成的膨胀波后,来流速度发生了改变,流线出现了抬升,后台阶区域出现了狭长的回流区。流场密度最大值约为喷流方式A、C的4.5倍。

对于喷流方式D,喷流角度为斜向上45°,流场相比喷流方式C,喷流两侧的回流区消失,并且喷流右侧的马赫盘也出现了消失。膨胀波角度相比喷流方式C更小。同样地,后台阶区域也出现了狭长的回流区。流场密度最大值小于喷流方式C,但同样大于喷流方式A和B。

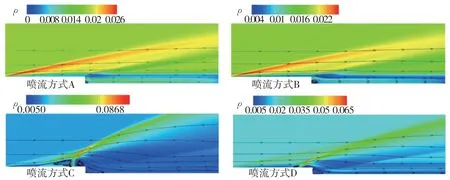
图9 不同喷流方式下后台阶流场密度云图和流线Fig.9 The density contour with streamlines for the cases of BFS

同样地,求得后台阶下游壁面热流系数,可以看到四种喷流方式下的壁面热流总体小于没有喷流冷却的标准流场。如图10所示,喷流方式A、B的热流系数接近。在壁面前段,热流系数为负,说明热传递方向相反,降温效果好。喷流方式C的冷却效果强于喷流方式D,并且两种喷流方式在上游壁面设置喷口的冷却方式的冷却效果均弱于在后台阶竖立面设置喷口的A、B喷流方式。

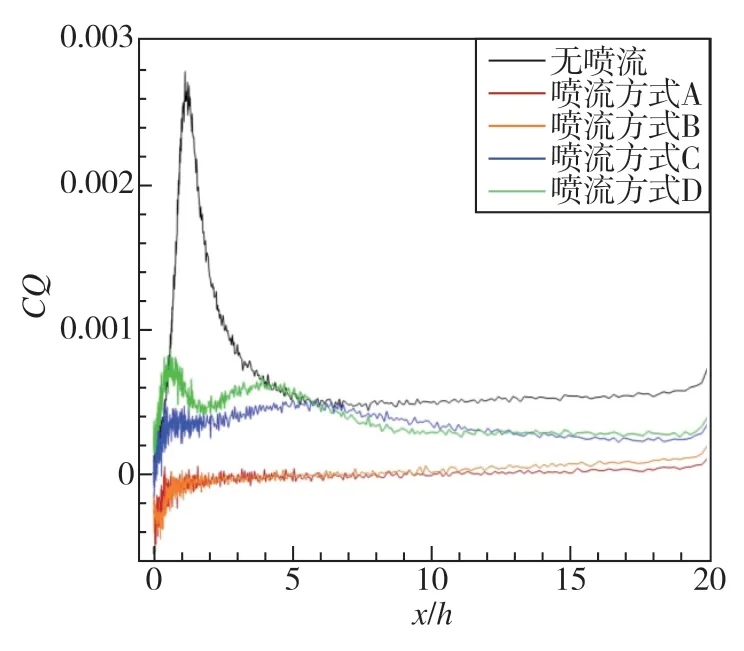
图10 不同喷流方式下后台阶流场热流系数Fig.10 CQ of BFS with different film cooling modes

3.3 不同高度后台阶气动光学效应

使用632nm的光束垂直于流场上方,在X/h=0~10平面布撒光粒子模拟光线照射。光束穿过流场最终到达后台阶下游壁面。在整个过程中,光束穿过了前缘激波、在附着激波、回流区等复杂的流场结构,如图11所示。

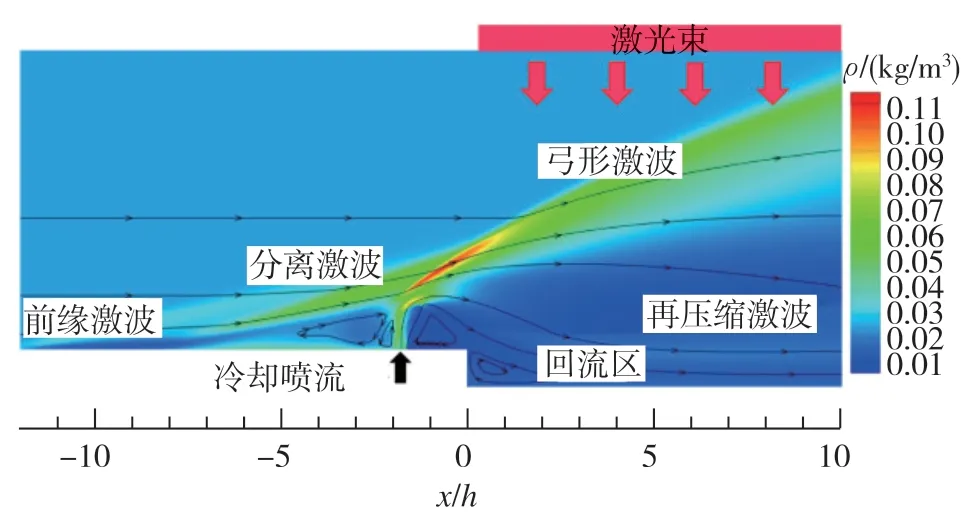
图11 光束布置位置示意图Fig.11 Schematic diagram of beam position

采用光线追踪算法,模拟光粒子在流场中的传输,得到光波的波面畸变。计算得到OPD,如图12所示。

图12 不同飞行高度下后台阶流场OPD变化Fig.12 OPD of BFS at different altitude

可以看到,对于无喷流后台阶流场而言,飞行高度越高,波面畸变越小。这是由于随着飞行高度增加,流场整体密度变小,并且不同流场结构本身的密度梯度的减小对光束传输的影响减弱。在高度为40km时,OPD的幅值是高度为30km时OPD幅值的1/5,并且随着飞行高度的增加,气动光学OPD的幅值更小。因此,可以认为飞行高度在30km以上时,流场的气动光学效应严重减弱,可以忽略不计。

使用光线追踪方法可以通过计算得到每一个光粒子穿过非均匀流场的最终位置与无流动介质的最终位置之间的距离,如图13所示。对所有光子的距离偏移进行平均,可以得到在该条件下图像的平均偏移,该平均偏移可以用来作为衡量气动光学效应的一个参数。

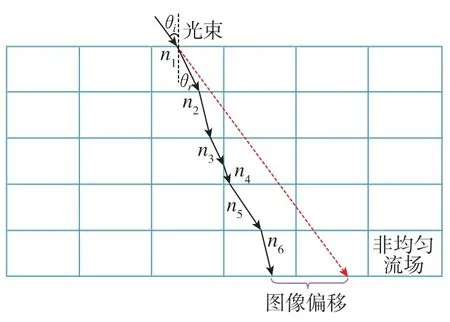
图13 光线通过非均匀介质的图像偏移Fig.13 Image shift of beam passing through inhomogeneous medium

设入射角θi为0.573°,通过计算得到不同飞行高度下每个光粒子图像偏移量的平均值,如图14所示。由图14可以明显看出,随着飞行高度的增加,后台阶流场的图像偏移急剧减小。当飞行高度增加到30km以上时,就可以忽略气动光学效应。

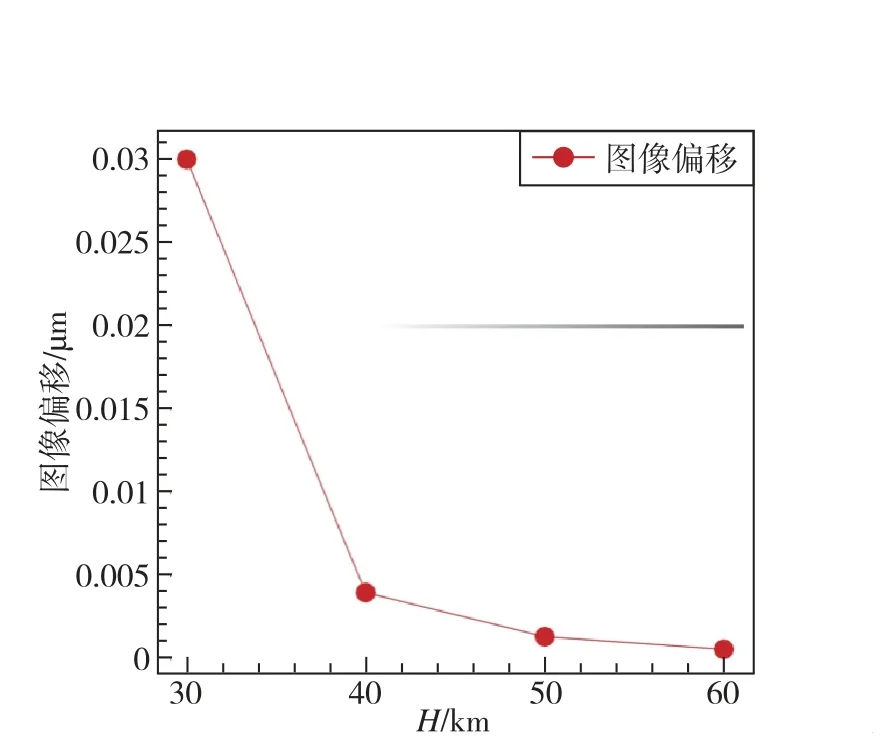
图14 不同飞行高度下后台阶流场的图像偏移量Fig.14 Image shift of BFS at different altitude

3.4 不同喷流方式后台阶气动光学效应

同样,对四种不同喷流方式的流场采用上文的光学参数进行气动光学计算,并用30km无喷流流场计算结果作为参照,可以得到波面畸变,如图15所示。

图15 不同喷流方式下后台阶流场OPD变化Fig.15 OPD of BFS with different film cooling modes

可以看出,对于四种喷流冷却方式,喷流方式C(即上游壁面垂直喷流)的OPD幅值最大,相比无喷流后台阶流场的幅值大一个量级。同时,其他三种喷流方式的波面畸变明显大于30km无喷流后台阶流场。

同样采用光线追踪计算光束平均偏移,可以得到不同喷流方式流场对图像偏折的影响,如图16所示。由图16可以看到,两种上游壁面开孔喷流方式C、D的图像偏移要比A、B两种喷流方式的图像偏移更大,并且喷流方式C的图像偏移远大于其他三种喷流方式。

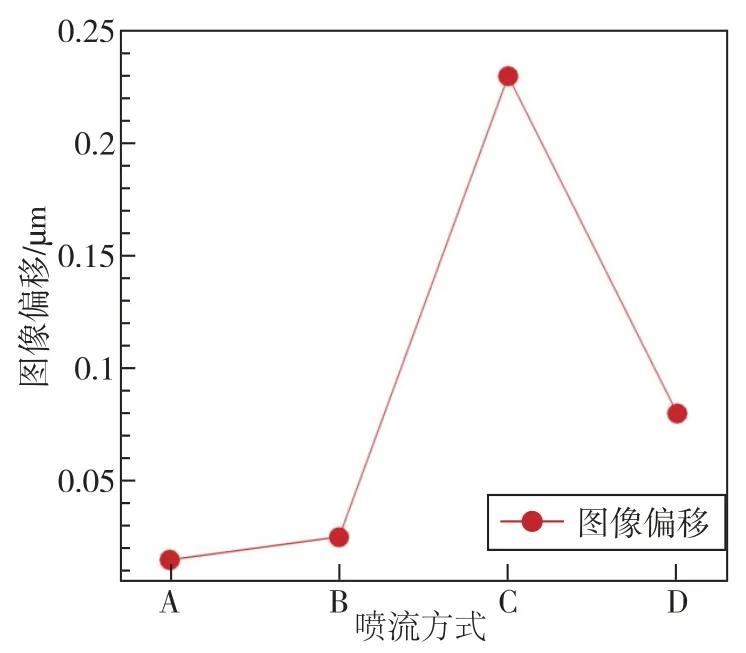
图16 不同喷流方式下的图像偏移量Fig.16 Image shift of BFS with different film cooling modes

综上所述,在四种喷流方式控制下的后台阶流场中,垂直喷流方式的气动光学效应最差,水平喷流和斜45°角水平喷流的气动光学效应相对较好,水平喷流方式A略好于喷流方式B。

4 结 论

对于不同飞行高度的后台阶流场,飞行高度越高,壁面的气动热效应越严重,但同时气动光学效应也随之减弱。当高度在30km以上时,可以忽略气动光学效应。

考虑到对后台阶壁面的喷流冷却,采取了四种不同的喷流方式。其中四种喷流方式相对于无喷流后台阶流场均能够改善壁面温度,起到冷却作用。其中,水平喷流的喷流方式冷却效果最好。在四种喷流方式中,垂直喷流方式的气动光学效应最严重,水平喷流方式的气动光学效应相对较弱,但均严重于无喷流流场。

综上所述,对于后台阶流场的冷却,建议采用水平喷流的冷却方式,这种方式在冷却下游壁面的同时不会带来更为严重的气动光学效应。

参考文献(References)

[1] HEDIN A E.Extension of the MSIS thermosphere model into the middle and lower atmosphere[J].Journal of Geophysical Research:Space Physics,1991,96(2):1159-1172.

[2]LE H,MOIN P,KIM J.Direct numerical simulation of turbulent flow over a backward-facing step[J].Journal of Fluid Mechanics,1997,330:349-374.

[3]ARMALY B F,DURST F,PEREIRA J C F,et al.Experimental and theoretical investigation of backward-facing step flow[J].Journal of Fluid Mechanics,1983,127:473-496.

[4]BISWAS G,BREUER M,DURST F.Backward-facing step flows for various expansion ratios at low and moderate Reynolds numbers[J].Journal of Fluids Engineering,2004,126(3):362-374.

[5]SHAHI M,KOK J B W,POZARLIK A.On characteristics of a non-reacting and a reacting turbulent flow over a backward facing step(BFS)[J].International Communications in Heat and Mass Transfer,2015,61:16-25.

[6]朱杨柱,易仕和,孔小平,等.基于NPLS的超声速后台阶流场精细结构及其非定常特性[J].物理学报,2014,63(13):271-276.ZHU Y Z,YI S H,KONG X P,et al.Fine structures and the unsteadiness characteristics of supersonic flow over backward facing step via NPLS[J].Acta Physica Sinica,2014,63(13):271-276(in Chinese).

[7]陈植,易仕和,何霖,等.基于NPLS的超声速层流/湍流后台阶流动精细结构研究[J].科学通报,2011,56(36):3057-3063.CHEN Z,YI S H,HE L,et al.An experimental study on fine structures of supersonic laminar/turbulent flow over a backward-facing step based on NPLS[J].Chinese Science Bulletin,2011,56(36):3057-3063(in Chinese).

[8]EATON J K,JOHNSTON J P.A review of research on subsonic turbulent flow reattachment[J].AIAA Journal,1981,19(9):1093-1100.

[9]张锋,易仕和,吴宇阳,等.基于NPLS的静压比对高超声速光学头罩冷却气膜影响作用研究[J].空气动力学学报,2019,37(5):762-769.ZHANG F,YI S H,WU Y Y,et al.Ratio of static pressure influence on cooling film of hypersonic optical dome based on NPLS[J].Acta Aerodynamica Sinica,2019,37(5):762-769(in Chinese).

[10]朱志斌,程晓丽,潘宏禄.超声速喷流混合流场大涡模拟[J].航空动力学报,2019,34(1):210-216.ZHU Z B,CHENG X L,PAN H L.Large eddy simulation of supersonic jet mixingflow[J].Journal of Aerospace Power,2019,34(1):210-216(in Chinese).

[11]邓放,韩桂来,孟宝清,等.超声速后台阶流动/射流相互作用的数值模拟[J].气体物理,2018,3(6):41-50.DENG F,HAN G L,MENG B Q,et al.Numerical simulation of supersonic flow/jet interaction at the double backward-facing step[J].Physics of Gases,2018,3(6):41-50(in Chinese).

[12]LI L Y,REN W,ZHANG B.Improved vertex weight for parallelization of DSMC in the near-continuum regimes[J].Journal of Aeronautics,Astronautics and Aviation,2014,46(2):88-95.

[13]REN W,LIU H,JIN S.An asymptotic-preserving Monte Carlo method for the Boltzmann equation[J].Journal of Computational Physics,2014,276:380-404.

[14]REN W,LIU H.Nonequilibrium hypersonic flows simulations with asymptotic-preserving Monte Carlo methods[C]//Proceedings of 29th International Symposium on Rarefied Gas Dynamics,Xi