怎样才能把握小学数学拓展习题的“度”
王小芳
(深圳市龙岗区福安学校 广东·深圳 518000)
0 引言
教育内容拓展作为当前教育改革深化与推进过程中一项重点内容,将学生的实践能力与创新精神作为中心,已经成为当前教育改革新方向。在素质教育全面普及的同时,我们会出现重视应试考试、忽视学生;重视基础教育,忽视能力培养等多种情况。目前在小学校园中,会出现社团、学生小论文、教师课堂讲座等多种活动形式,通过该方式促使学生的思维空间得以拓展,但是却未能认识到拓展性课堂的重要性,究其根本就是因为我们没有把握好数学拓展课当中的“度”。
1 对小学数学拓展习题进行优化的必要性与具体选择对象
1.1 对小学数学拓展习题进行优化的必要性
在数学拓展习题当中,因为涉及到的知识内容具备极强的综合性,所以应当帮助学生深入地了解知识,激发学生学习兴趣,调动学生参与到拓展习题教学当中的主动性,最终可以提高学生的思维能力。与此同时,在对小学数学拓展习题进行规划过程中,也有利于提高与培养学生对数学的理解能力、解题能力、动手实践能力,保证学生在日后生活中可以利用所学习到的数学知识,去解决数学问题,提高自身的综合能力。
1.2 具体选择对象
拓展两个字都有其对应的含义,拓指的就是扩充、开辟,展指的就是展开。在拓展性学习中会涉及到显性部分,而该部分指的就是在原有的基础上开辟、拓展新的学习领域,从教学方面来看,指的就是在教学中学生的学习方法、学习形式、学习内容都有所增加,并且朝着优化方向发展下去,能够有效提高学生的学习能力。拓展课广泛存在于学习领域,面对的对象不仅包括学生。在拓展课中希望学生通过动手操作、实践训练、阅读内容等方式,获得更多收获,感受不一样的成功。
2 小学数学拓展习题中的三个“度”具体内容
在数学课堂教学中,数学习题是其中重要组成部分,他也是培养学生数学思维、帮助学生巩固理论知识的关键内容。所以教师在设计数学习题时,对课堂知识进行拓展,保证课堂学习资源更加地丰富,由此培养与提高学生举一反三、由此及彼的能力。但是在数学实践过程中,很多教师对课堂认知与设计存在偏差,片面地认为设计难题、偏题、怪题能够提高学生的数学学习能力,这种想法必然是错误的,这是因为教师没有把握好教学中的“度”,导致课堂拓展进入极端化,失去其原有的作用与价值,同时也会导致学生的学习积极性被不断降低,最终影响学习成绩。如何才能在小学数学教学中,对拓展性习题设计当中的“度”做好正确把握,笔者认为需要从下述三点出发:
2.1 把握拓展习题广度,提出实效性
在课堂教学中,数学习题占据着重要地位,教师想要提高学生的学习成绩与个人素养,实现新知识的发展与拓展,那么拓展性习题成为其中一项有效的方法。通过该方法,保证学生可以内化新知识、理解新知识。在拓展延伸时促使学生对所学知识进行迁移,培养学生的发散思维与创新能力,如果教师未能把握好习题拓展的“火候”,极有可能加重学生的课堂负担,导致学生学习兴趣被影响。所以在设计拓展性习题时,教师应当对其中的“度”进行准确把握。
一是突破重点知识部分。在对重点知识作出拓展时,因为课堂时间有限,所以必须把时间用在刀刃上,教师应当把握好习题投放的量,不可为求全面,而出现主次不分情况。在选择习题过程中,必须将针对性原则加入其中,保证课堂教学中讲述的知识具备完整性,同时有利于学生达成学习目标。
二是保证习题面对的是班级全部同学,在数学课堂中,学生作为教学主体,因此教师必须清楚地认识到学生在课堂中的重要性,保证所有活动面对的是整体学生,充分尊重每个学生在学习时提出的要求,不能将课堂打造成个别同学展现自我的舞台。所以在设计拓展性习题时,不能将其作为点缀,而是应当控制其难度,保证符合全体学生需求。
比如在课堂教学中,有一道题目是:同学们,通过观察表1的百数表,找到九的倍数,并且涂出不一样的颜色。
(1)观察9的倍数,他们都有什么特点?
(2)这些数在排列过程中,会呈现什么样的特点呢?与其他小伙伴互相说说自己的想法。
(3)如果将表1扩充到200,并且继续找出99之后是9的倍数的数,看看他们在表中什么位置呢?通过做一做的方式,来验证你的猜想。
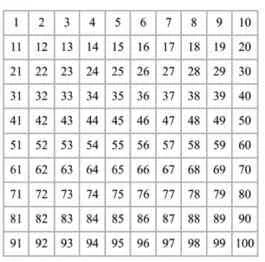
表1
学生通过自己动手操作与应用课堂中所学习到的知识都能发现其内在规律,但练习的目的并不局限于此,教师在学生解决问题(1)问题(2)之前,可以将比一比方式加入其中,学生们通过亲自动手画一画9的倍数,找到其中的规律,查看哪个学生会完成得最快,大部分学生都能快速得到正确结论。在题目(3)时,因为要求学生观察99以后的数字哪些是9的倍数,教师可以引导学生对问题(1)问题(2)的答案进行拓展,使学生开动脑筋,拓展学生的思维,帮助学生正确的去观察数字、了解数字,最终掌握该方面知识。
在练习过程中,紧紧围绕9的倍数数字特征,与课堂教学内容紧密结合,同时也能起到提高与发展的作用,保证学生可以熟练地使用自己接触到的新知识,拓展与启发学生的思维,随后教师也可以要求学生根据所掌握的规律,探索3的倍数、6的倍数与9的倍数有什么样的联系,对所学内容进行巩固的同时也能复习一些简单的知识,保证学生的数学学习水平得以提高,确保所有学生都能从课堂学习中获得收获。
2.2 拓展习题必须把握长度,强调其中针对性
在新课标中明确强调,数学教学必须从学生已经具备的认知规律、生活经验、知识水平等出发,所以教师在布置练习内容时,必须将学生特点与教材内容作为根本,从学生实际学情出发,提高学习当中的针对性。教材作为对学生做出系统化培养的关键方法,教师在设计习题时,应当围绕教材知识点,对知识进行整合、重组,由此更好实现教学目标。如果在设计教材内容时脱离教材,这就好比无水之源、无本之木,无法达到培养目的。练习设计中一个重要的依据就是学情,将拓展性练习设计加入其中,需要从学生的最近发展区出发,不能过于简单,也不能超出学生能力范围,必须把握好其中的“度”。教师必须充分掌握学生的认知规律,在设计题目时,达到“学生跳一跳,就能够得到”的效果,最终使学生的知识技能得到发展。
比如学生在学习完长方形与正方形长度、面积计算公式之后,教师为学生提供了以下拓展性习题:
(1)小明家的厨房准备铺地砖,该厨房的长度为30分米,宽度为24分米,需要选择边长是多少分米的方砖,既能铺满厨房,又避免浪费呢?(地砖边长要求是整分米数)
(2)张大爷家有一块长方形的小菜园,菜园的长度为26.4米,宽度为20.1米,张大爷想用篱笆将菜园围起来,其中有一个门为1米宽,需要多少米的篱笆呢?张大爷打电话咨询了两家公司,甲公司报价是每米需要1.3元,乙公司是将菜园全部围起来后价格是128.8元,如果两家公司篱笆质量是相同的,我们需要帮张大爷想一想,哪一家公司更加划算呢?
上面这两道题目都与学生所学到的知识相关,题目(1)要求学生算出厨房的面积,随后利用厨房面积大小,找到最合适的方砖,这道题具有一定的思维拓展性,同时也是对生活知识进行拓展。在解题过程中,学生需要在脑海中构建相应的图形,避免解题出错。题目(2)是对长方形的边长进行考察,在解题过程中,学生能够了解边长计算的本质,保证学生对(长+宽)×2理解更加深入。上述两道题目均难度适中,学生在经过一段时间的练习之后,能够对边长、面积之间的关系理解更加透彻,保证学生的思维得以发散。
2.3 把握拓展习题的高度,注重其中激励性
在数学教学中,如果学生从中获得更多体验,必然会激发学生的学习兴趣,使其主动投入到学习当中来,提高学生学习效率,帮助学生体验成功快乐。所以为学生提供获得成功的体验,可以帮助很多学困生逐渐发现学习乐趣。在对拓展性习题进行设计时,必须把握好其中的高度,保证高度位于学生最近发展区,只要学生努力,就能获得成功。如果高度不够,那么就很难激发学生的努力意愿,最终影响学习兴趣。比如某道题目为:如图1所示利用剪一剪的方法,将图形A变成两个部分,随后将其拼成图形B,如果想拼成图形C,同学们应该怎么去剪呢?
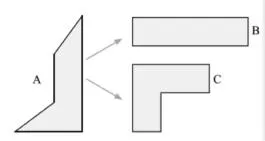
图1
在面对这样的题目时,需要学生开动脑筋或者动手操作,往往会激发学生的学习兴趣,如果学生不能打破思维定式,很难得到正确的图形,在这时就要求学生具备思维拓展性与知识拓展性,这对于学生而言,也是一种挑战。教师需要对自己所看到的内容进行重新的观察,与实际情况相结合。在学生经过多次实验后,如果获得正确结果,教师需要鼓励学生,使他们感受到成功的喜悦。与此同时,因为每个学生的思维方式是不同的,同学们会根据自己的想法,得到各种各样的图形,在同学之间也起到相互启发的作用,保证学生思维得以发散。
3 结束语
综上所述,促进学生全面发展,成为新课改的重点,在这时就要求教师打破原有的教学思路,将教学方案面向整体学生。在对拓展性练习进行设计过程中,应当将适度性原则与全面性原则加入其中,保证学生通过练习,对所学知识进行巩固,同时也能适当的提高与迁移知识,保证学生的数学素养得以有效提高。

