计及DR的电-气综合能源系统的鲁棒优化调度

章 健， 张玉晓， 朱永胜， 熊壮壮， 谢加新， 祝方圆

(1.郑州大学 电气工程学院，河南 郑州 450001； 2.中原工学院 电子信息学院，河南 郑州 450007；3.国网山西省电力公司晋城供电公司，山西 晋城 048000)

0 引言

近年来，由于人类社会面临能源危机和大量分布式能源(distributed generation, DG) 的接入带来的高渗透率等问题，能源互联网(EI)的概念应运而生，成为解决问题的关键，也是未来能源发展的新模式[1]。天然气相较于一般一次能源，更清洁环保，其网络与电力网络具有相似的能量流属性，与电力网联系紧密，从而使得电-气综合能源系统(integrated electricity-natural gas system, IEGS)成为EI的基础和过渡，因此研究IEGS的特性具有深远的意义[2]。

由于电力网与天然气网的耦合作用，使得电力网中的DG波动传播到气网络，威胁整个系统的安全。电转气(power to gas，P2G)技术[3]的出现为解决这一问题提供了新思路，其将电能转化成天然气进行储存，可有效加强两系统间的耦合，并可消纳DG，降低弃电率。Vandewalle等[4]研究了P2G对IEGS运行的影响。杜琳等[5]论证了P2G有提升负荷供能率和降低弃风水平的作用。故提升P2G的电转化量，可提高IEGS的耦合性，对加强能量间的转化和提高DG的消纳有重要作用。

需求响应(demand response,DR) 通过制定合理价格来引导用户用能行为，转移高峰用电以减少弃电率，对DG消纳和提升IEGS的运行效率具有重要作用。Kirschen等[6]通过弹性矩阵来反映负荷与电价的关系，奠定了价格型DR研究的基础。曾鸣等[7-9]从DR的不确定性、新能源的消纳和用户满意度等方面，研究了价格型需求响应对电力网络优化运行的影响。然而对于DR在IEGS中的影响分析国内外研究尚少。张伊宁等[10]考虑价格型需求响应机制；Zhang等[11]考虑了DR的爬坡能力;曾博等[12]在IEGS中加入DR的不确定性，建立一种动态概率能流计算方法。以上文献仅考虑电力网络中的需求响应，忽视了天然气网络中的DR对系统灵活性和稳定性的影响，且采用的定价模型不能体现电价如何引导用户行为来促进新能源的消纳。实际上，合理制定定价模型，能更有效地引导用户用能行为，以降低DG的弃电率。

另外，卫志农等[13]考虑需求响应和电转气，建立IEGS的优化模型，实现风电消纳的目标，但未考虑风电的不确定性。实际上，DG出力的波动性将增加IEGS运行调度的风险。结合Arias等[14]的研究，目前解决DG不确定性的方法有随机规划、模糊规划以及鲁棒优化，前两者有概率分布不确定和受样本数据及决策者主观性影响较大等缺点，而鲁棒优化因仅需模拟不确定边界等优点被广泛使用。

综上，本文建立了计及DR的IEGS鲁棒优化调度模型。并采用修改的IEEE33节点电力网和比利时20节点天然气互联系统仿真，论证文中模型能够促进DG消纳和增强系统的耦合性，与确定性优化模型对比，说明该模型对DG的波动具有良好的适应性。

1 DG出力不确定集

文中考虑风力和光伏两种DG，针对DG出力不确定的特性，可根据典型地区历史数据进行统计预测，由于鲁棒优化模型以适应DG不确定性发展为目标，其核心在于制定恶劣场景下的决策方案，因此引入DG的不确定性集，公式如下:

εmin≤ε(t)≤εmax}。

(1)

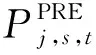
根据凸优化理论，极值存在于多面体解空间某端点处，需要通过制定相应规则来筛选端点场景，即极限场景或恶劣场景。可通过以下规则，生成简单有效的不确定性端点场景，规则如下：

(1)考虑各时段值取限值的场景，取以下两种情况：

(2)

(2)取满足全时序总量为限值的场景，即

(3)

2 电-气综合能源系统鲁棒规划模型

2.1 目标函数

本文优化模型旨在研究IEGS能量传递和对DG消纳的影响，因此建立以下目标函数：

(4)

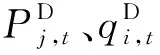
2.2 电力网络模型

(1)支路潮流约束：

(5)

(6)

(7)

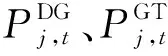
(2)安全约束：

(8)

式中：Vj,max、Vj,min、Iij,max分别为节点电压幅值上、下限和电流幅值限值。

(3)配电网关口约束。为了防止主动配电网关口功率波动对输电网的电能质量的影响，对其进行约束如下：

(9)

(4)分布式电源出力。文中考虑风光两种不同的DG，由于二者有相似的特性，现将其简化分析，建立如下模型：

(10)

式中：φ为DG的功率因数角。

2.3 天然气网络模型

(1)气源。气源点向天然气网络注入天然气，每个气源点供应流量的上下限满足以下约束条件：

(11)

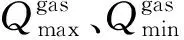
(2)管道。本文采用树型无环网天然气系统，根据天然气网络的实际情况，在1 d内气流方向几乎不变[15]，则管道方程具体可描述为以下形式：

(12)

(3)流量平衡。根据流量守恒定律，任意节点的气体总流入量等于总流出量。

(13)

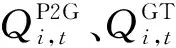
2.4 电-气耦合元件约束

电-气综合能源系统中由燃气轮机机组和P2G装置作为耦合元件。

(1)燃气轮机机组约束：

(14)

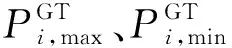
(2)P2G装置约束：

(15)

3 电-气互联系统需求响应建模

3.1 电力负荷需求响应模型

本文将电力负荷分为居民、商业、工业用电3种，依据价格信号刺激用户自发转移用能时段，实现削峰填谷的作用。其模型如下：

(16)

电价约束：

(17)

响应后的有功无功约束：

(18)

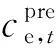
3.2 天然气负荷需求响应模型

天然气与电力均为重要资源，具有相似的商品属性，为进一步研究需求侧对 IEGS作用，类比电力负荷，天然气负荷模型如下：

(19)

为进一步加强 IEGS的耦合性，提高系统的稳定性，考虑气负荷与电转气量的差值，添加定价约束：

(20)

(21)

4 模型化简

在本文模型中，目标函数、电网络支路潮流及天然气管道方程中含非线性约束，为方便快速求解，可将混合整数非线性规划(MINLP)问题转化为混合整数线性规划(MILP)问题。

4.1 二阶锥规划处理平方项

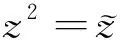
(22)

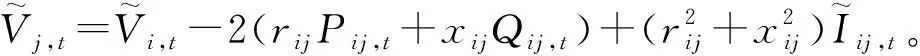
(23)

安全约束变为：

(24)

同时对式(7)、(12)松弛优化得到对应的二阶锥形式：

(25)

(26)

4.2 McCormick方法处理双线性项

对于目标函数中售电售气收入均为双线性项，采用McCormick法将其线性化，令

(27)

其中Δj,t满足以下约束：

(28)

式中：Δj,t为辅助变量。

同理售气收入亦可采用上述方式进行线性化处理。

5 仿真论证

5.1 算例参数

文中采用修改的IEEE33节点电力系统与比利时20节点天然气系统进行仿真验证。天然气系统包含20个节点，21条输气管道，2个气源点，将天然气负荷归算为电力单位。图1为模型的求解流程图；图2为电、气负荷出力曲线。

图1 模型求解流程图Figure 1 Flow chart for model solving

图2 电负荷、气负荷出力曲线Figure 2 Load profile of electric and gas

该系统的风电出力和光伏出力的均值和波动范围分别见图3、4；各时段电价见图5；表1、2给出了各类型装置的参数和IEGS求解参数。计算平台为系统硬件环境Intei(R) Core(TM) i5-2 410 M CPU，2 G内存，程序在Yalmip上建模，于MATLAB R2016b环境下用CPLEX12.7算法包进行计算。

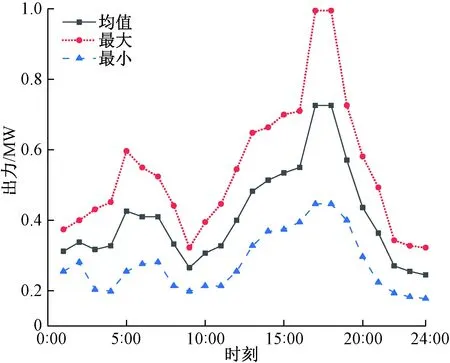
图3 风电出力Figure 3 Wind power output

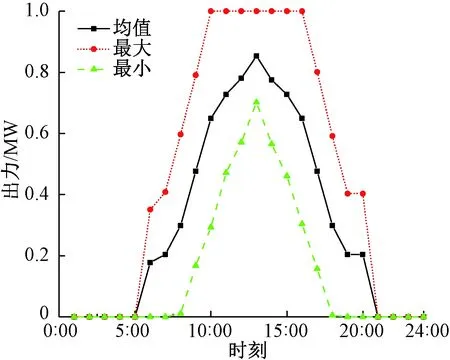
图4 光伏出力Figure 4 Photovoltaic output

5.2 电-气系统不同需求响应分析

5.2.1 价格约束系数对系统的影响

电价与气价约束系数，对电、气价格的定价具有重要作用，由于电、气负荷具有相似的价格属性，为方便计算，认为二者相同。其中电价气价约束的波动范围为基准值的±50%，需求响应容量上下限为基准值的±15%。现对价格约束系数取不同的值进行研究，结果如表3所示。

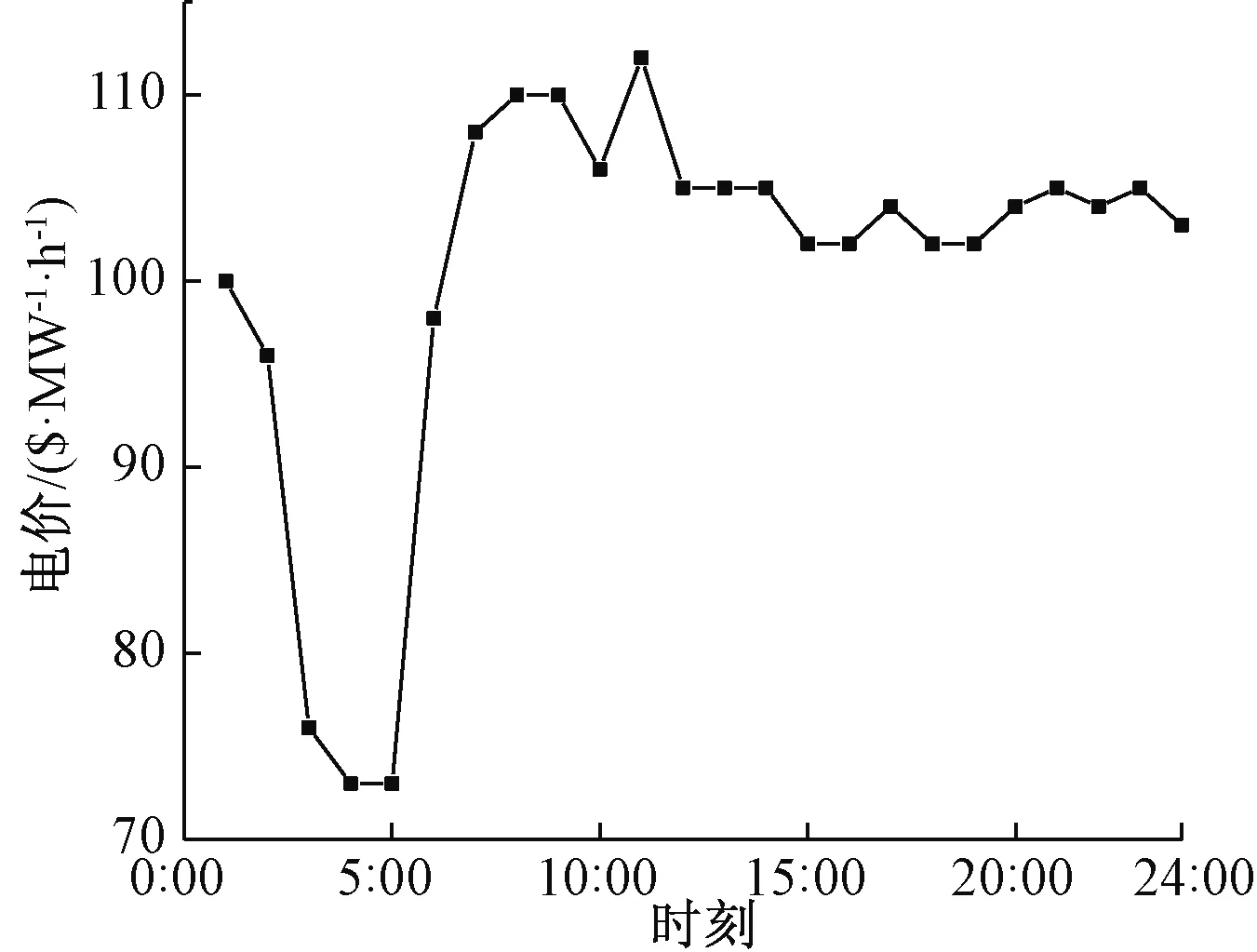
图5 购电电价曲线Figure 5 Electricity purchase price curve

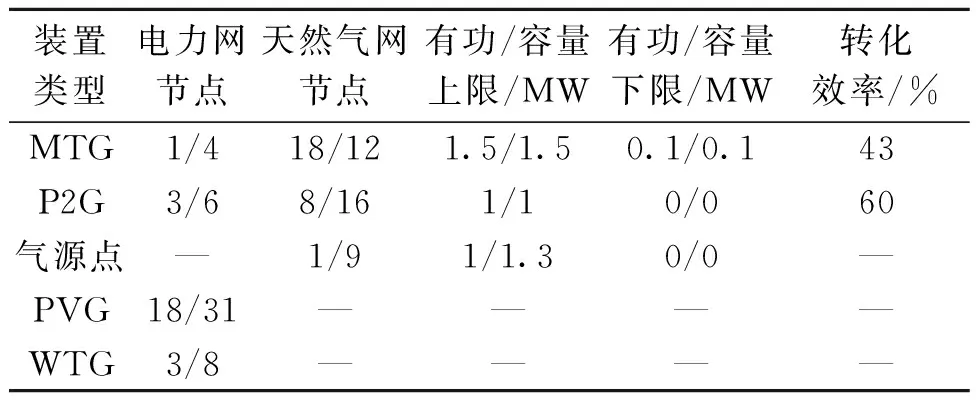
表1 各类型装置参数Table 1 Parameters of each type of device

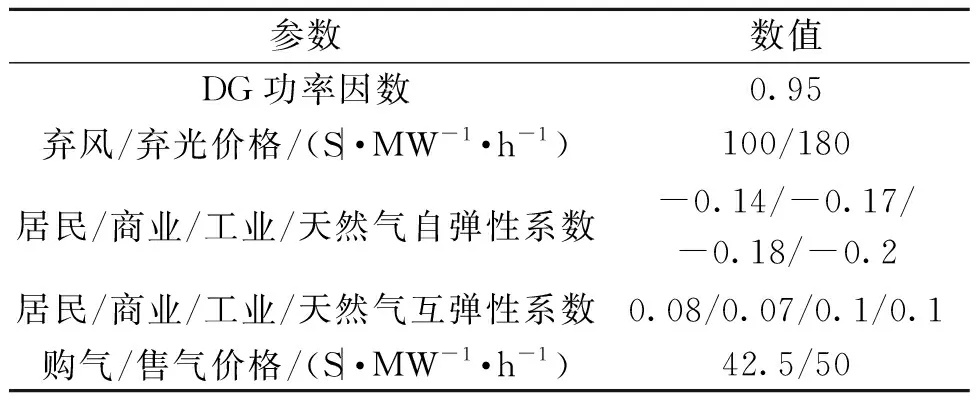
表2 模型求解参数Table 2 Parameters for solving the model

由表3可以看出,随着γ的增大,利润逐渐降低，总弃电率下降，电转气总量逐渐增加。当γ增大时，对应的电价、气价变化增大，由于价格变化幅度越大越易刺激用户参与需求响应，使负荷曲线变化幅度增大和DG的消纳能力增强，故价格调节对弃电有显著影响。γ=6或8时，总弃电率较小，但利润较低，电转气总量增幅相对分别为14.85%和6.90%;γ=4时对比γ=2时电转气总量增加了42.24%，极大增强了电-气系统之间的耦合，提高了系统可靠性和稳定性，弃电率进一步降低。

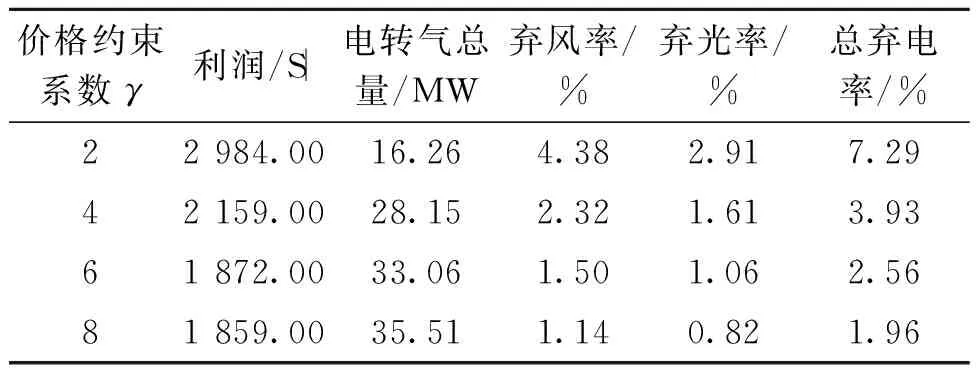
表3 不同γ对系统影响分析Table 3 Analysis of the impact of different γ in system

综合考虑，文中选取γ=4，既满足加强需求响应调节能力、DG的消纳能力的要求，又使电-气综合能源系统间耦合度增加。

5.2.2 不同DR对电-气综合能源系统影响分析

为验证基于价格约束系数的需求响应对消纳DG能力和运行效率提升的有效性，设置3种情景进行对比分析。情景1：不考虑需求响应；情景2：考虑不计及价格约束系数的一般需求响应；情景3：考虑计及价格约束系数的需求相应。不同情景结果对比分析如表4所示。采用蒙特卡罗随机生成1 000个场景，并选取16个典型场景进行分析。

其中表4中数据为各个变量的均值，如利润并非收入与成本的直接相减。可以看出，对比于情景1、2，采用本文PR模型后，总弃电率大幅度下降，得益于电转气总量增加，使更多的DG发电量通过PIG转化为天然气，增强了IEGS的耦合度，并提高了售电售气收入。然而由于一部分电能的转化，也在一定程度上增加了电网络的购电成本。

对比情景1，情景2加入需求响应后，能明显增加DG的消纳率，且利润增加。图6为处于最恶劣场景的不同情景下IEGS能量交换曲线(取利润最大的某一场景)，可以看出采用本文模型远远领先其他情景的IEGS的能量交换量。结合电力负荷曲线图，在负荷低谷期(0～10 h、22～24 h)时，电转气、气转电波形都处于峰值，电-气系统间能量的传递能力加强；在负荷高峰期(16～21 h)时，系统电-气之间的互转量都明显降低，电转气值减小到零，使更多的风光发电用于电力负荷损耗，使DG消纳量增加，弃电率减少。所建模型通过对需求响应价格约束系数的定义，一方面实现对DG的消纳，另一方面增强了系统的耦合性，使DG发电量能够在系统中灵活转移，促进能量间的交换。

表4 不同情景下结果对比分析Table 4 Comparison of results in different scenes

图7为不同情景下电价变化，情景2中工业负荷电价波动范围大，峰谷差达到98.6S|，一半时间处于电价极端值，居民、商业电价几乎一成不变且波动不规律，不利于用户参与需求响应，对比图2不能根据负荷的变化达到削峰填谷的目的。情景3中电价基本在基准值上下波动，峰谷差较小，更具有针对性。结合对应的电力负荷曲线，电价的波动规律与负荷大致吻合，在负荷高峰期时电价增加，低谷期时电价降低，这将极大促进用户参与需求响应的积极性，使消纳DG能力增强。

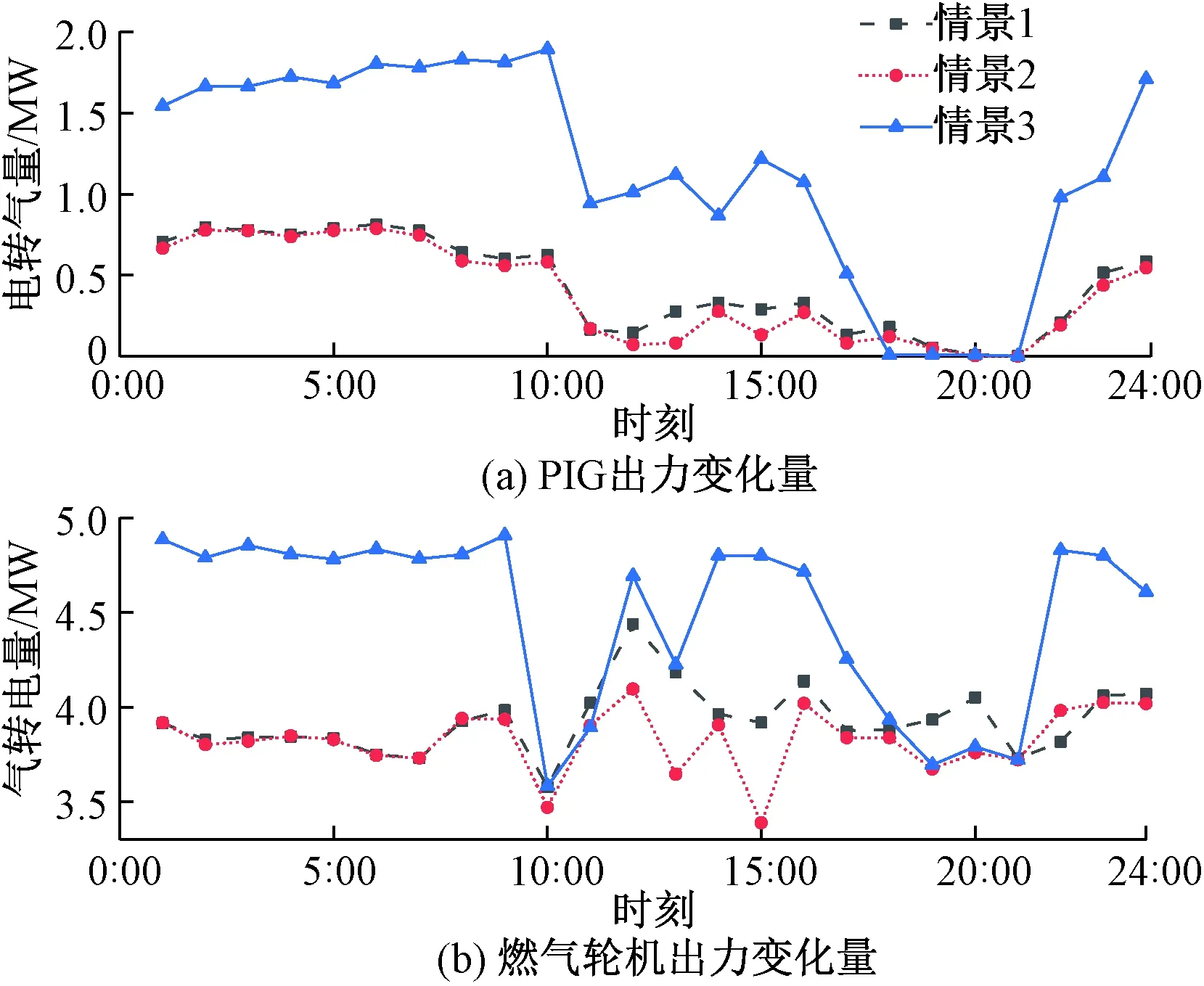
图6 不同情景下电-气交换量Figure 6 Exchange capacity of electric-gas in different scenes

图7 不同情景下电价对比Figure 7 Comparison of electricity price in different scenes

5.3 电-气互联系统的鲁棒性分析

为分析鲁棒模型的性能和DG在不同波动范围下的运算结果，对系统的鲁棒性模型与传统的确定性模型对比分析，如表5所示。

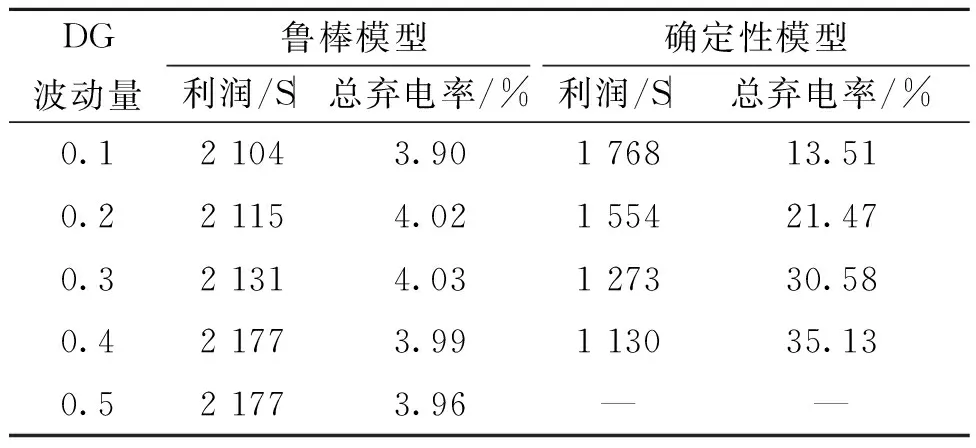
表5 不同模型对波动范围的对比分析Table 5 Comparative analysis of fluctuation range in different models

上述值为所有场景中的均值，可见随着DG波动性的加强，确定性模型产生更多的弃电成本，导致利润降低，且弃电率大幅度增加，当DG波动量为0.5时，系统无可行解，鲁棒性差。而鲁棒模型能更好地平衡系统的稳定性，弃电率能够保持很低且变化不大，抗干扰性强。由于IEGS中能源之间动态的交换调节作用，利润变化不明显，大于0.4后几乎不变，当增到0.8时系统模型无可行解。说明鲁棒模型对波动偏差也具有一定的极限，因此在实际应用中应合理选择DG波动偏差。

5.4 算法验证

为验证本文MILP的可行性和二阶锥及McCormick法的有效性，现将其与原始MINLP进行对比分析，对MINLP运用粒子群智能算法求解，如表6所示。由表6可见，直接求解MINLP耗时长，而转化为MILP后，求解速度大大提高。

表 6 不同算法下的求解信息对比Table 6 Comparison for solution information under different algorithms

6 结论

建立了针对消纳分布式能源和加强IEGS耦合性的需求响应模型，并考虑DG出力的不确定性，运用二阶锥和McCormick法建立了计及DR的IEGS的鲁棒优化调度线性模型，经过算例验证，得到如下结论：

(1)相较于一般需求响应，在选择合适的电价、气价约束系数后，对清洁能源的消纳和系统间的耦合性上，本文模型具有更大的优势。

(2)随着DG波动性的增加，本文鲁棒模型弃电率始终较低，性能更好，但对波动范围也存在一定极限，故在实际情况中应合理选择波动偏差。