基于Gudehus-Bauer亚塑性模型的面板堆石坝应力变形研究

陈泽钦， 刘国明

(1.国网福建省电力有限公司电力科学研究院，福建 福州 350007； 2.福州大学 土木工程学院，福建 福州 350108)

0 引言

近年来，一种新型的亚塑性本构模型被用于描述堆石料应力-应变关系。该模型以非线性连续介质力学为理论基础，以张量分析为计算工具，直接建立了颗粒体材料的应力率与应变率的关系。同时，该模型还减少了一些人为的假定，较为客观地反映了材料复杂的力学特性。

目前国内外研究人员已建立了较多的亚塑性本构模型，该模型最早由Kolymbas[1]针对砂料提出，并被广泛推广。Gudehus[2]、Bauer[3]针对砂料提出了Gudehus-Bauer亚塑性本构模型，在模型中引入了密度因子和刚度因子，考虑了砂粒料的孔隙比变化特征和临界状态，较好地描述了砂料的主要力学特性。Herle等[4]研究了亚塑性模型，并对其参数确定方法作了详细的介绍。Fuentes等[5]基于亚塑性理论提出颗粒间应变的空间屈服函数，反映了应变历史状态。Wang等[6]提出一种改进的边界面亚塑性本构模型，描述了松砂或者密砂不同阶段的循环加载的力学特性，考虑了材料状态相关剪胀性理论和累积塑性应变对塑性模量的影响。Lin等[7]基于微亚塑性模型理论，采用离散元法和连续统法模拟颗粒料的双轴试验和简单剪切试验，获得了较好的成果。岑威钧等[8-9]在亚塑性模型中增加体变控制项，且取-0.04，并用于描述堆石料应力变形特性，改善了模型模拟的堆石料体积应变曲线。吴长彬等[10]、岑威钧[11]建立了拟合参数与平均压力的关系。Xiang等[12]考虑了不同应力路径的影响，提出了增量非线性亚塑性本构模型，获得了试验验证。明华军等[13]引入考虑颗粒破碎堆石料特征孔隙比的表达式，改进的模型较好地描述堆石料的力学特性。陈泽钦等[14]在Wang-Wu亚塑性模型的基础上，提出了七参数模型，较好描述了堆石料应力变形特性。王仁超等[15]研究了亚塑性模型自适应隐式和显式两种不同的积分算法，并在ABAQUS平台开发UMAT-VUMAT接口，有效地实现了亚塑性模型数值分析应用。唐扬[16]推导了主应力空间的亚塑性模型稳定面，并应用于滑坡稳定性数值计算，较好地分析了潜在不稳定区域。Osinov等[17]基于亚塑性模型进行隧道的动力数值分析，研究了衬砌和土体的应力和变形。Hleibieh等[18]通过与不同边界条件和初始应力状态下获取的砂土试验数据对比，认为亚塑性模型可以有效地描述不同动力响应条件下砂土的应力-应变特性。本文利用改进的Gudenhus-Bauer亚塑性本构模型对面板堆石坝进行了非线性有限元应力分析。

1 Gudehus-Bauer亚塑性模型

Gudehus-Bauer亚塑性模型由Gudehus等[2-3]提出，其模型为：

(1)

其中Gudehus-Bauer模型中的刚度因子fs和密度因子fd表达式如式(2)和式(4)所示：

(2)

(3)

(4)

式中：α和β为模型的拟合参数；ps为平均压力，ps=-tr(σ)/3；ei0、ec0和ed0分别为零压力下ei、ec、ed对应的界限孔隙比；hs为颗粒硬度，kPa；n为拟合指数。

下界孔隙比ed、临界孔隙比ec和上界孔隙比ei随平均压力ps增加而减小[2]，各孔隙比的变化规律如式(5)所示：

(5)

在无量纲因子a1中引入了Lode角θ，则a1为偏应力方向的函数，如式(6)所示。在常规三轴试验时，无量纲因子a1为常数[19]，即a1=1/c1，

(6)

因此，Gudehus-Bauer亚塑性模型共有8个参数，分别为α、β、φc、hs、n、ei0、ed0、ec0。

2 Gudehus-Bauer亚塑性模型的改进

2.1 拟合指数α和β改进

根据文献[4, 20]介绍的方法计算了坝体填筑料的Gudehus-Bauer亚塑性本构模型参数中的6个参数，即颗粒硬度hs、拟合指数n、不同零压力下界限孔隙比ei0、ed0、ec0和摩擦角φc等参数，如表1所示。

α=k1ln(σ3/pa)+b1。

(7)

式中：k1为斜率，b1为截距，均为拟合参数。

β=lnA/lnB。

(8)

式中：B=ei/e；

由式(8)可知，β与ps具有较为复杂的关联，为简化这一关系，假定β与ln(σ3/pa)具有式(9)的关系：

β=k2ln(σ3/pa)+b2。

(9)

式中：k2为斜率；b2为截距，均为拟合参数。

由以上方法即可求取Gudehus-Bauer亚塑性模型的8个参数结果，如表1所示。

表1 模型参数求取结果Table 1 The result of the model parameters

根据表1的参数结果，用Gudehus-Bauer亚塑性模型模拟了主堆石料三轴压缩试验，如图1所示。

图1 主堆石料的三轴试验值与模型模拟结果Figure 1 The test values and the model simulated values of major rockfill materials in triaxial test

由图1可知，Gudehus-Bauer亚塑性模型描述的堆石料偏应力曲线与试验值吻合较好；描述的体积应变曲线与试验值的吻合程度较差，该模型不能较好地反映堆石料的应变状态，需进一步改进。

2.2 针对堆石料的改进

(10)

式中：λ为体积应变调整参数，为拟合参数。

用改进的Gudehus-Bauer亚塑性模型模拟了堆石料三轴压缩试验，体积应变曲线与试验值更为吻合，有效改善了原模型这一缺点。

3 工程应用

3.1 工程概况

某抽水蓄能电站大坝坝型为面板堆石坝，坝顶高程299.90 m，正常蓄水位294.00 m，最大坝高75.1 m。面板厚度采用渐变的方式，顶部厚度0.3 m，底部厚度0.5 m，坝坡及坝体材料分区如图2所示。

图2 大坝河床断面(m)Figure 2 The riverbed section of the dam(m)

3.2 计算情况及材料参数

坝体分为41个横断面，坝体有限元计算网格划分如图3所示，单元总数为7 929，结点总数为8 420。在有限元计算中，采用28级进行加载以模拟坝体施工过程，前18级模拟堆石体施工过程，19级和20级分别模拟面板施工和坝顶施工，第28级大坝蓄水至正常蓄水位为294 m。

图3 堆石坝三维网格Figure 3 FEM mesh of dam

混凝土面板和坝体堆石料采用三维实体单元模拟,面板垂直缝和周边缝采用无厚度Goodman连接单元模拟，单元的参数取值参考天生桥一级面板堆石坝的力-位移模型试验成果[21]。在材料性质相差较大的接触面设置无厚度Goodman接触面单元模拟，如混凝土与垫层料接触面，趾板与堆石体接触面，单元参数从文献[21]取值。

将改进的Gudehus-Bauer亚塑性模型的分析成果与邓肯E-B模型和沈珠江双屈服面模型数值成果进行对比。其中，采用中点增量法求解非线性方程组，双屈服面模型的屈服面中广义剪应力q采用八面体剪应力，邓肯E-B模型采用平均主应力p和广义剪应力q等效代替σ3和(σ1-σ3)[21]。

3.3 坝体应力变形分析

竣工期坝体仅受自重时，坝体沉降量和水平位移的最大值及其变形规律与面板堆石坝常见的变形规律较为吻合，如图4和图5所示。

图4 竣工期沉降量(cm)Figure 4 The vertical displacement in construction period(cm)

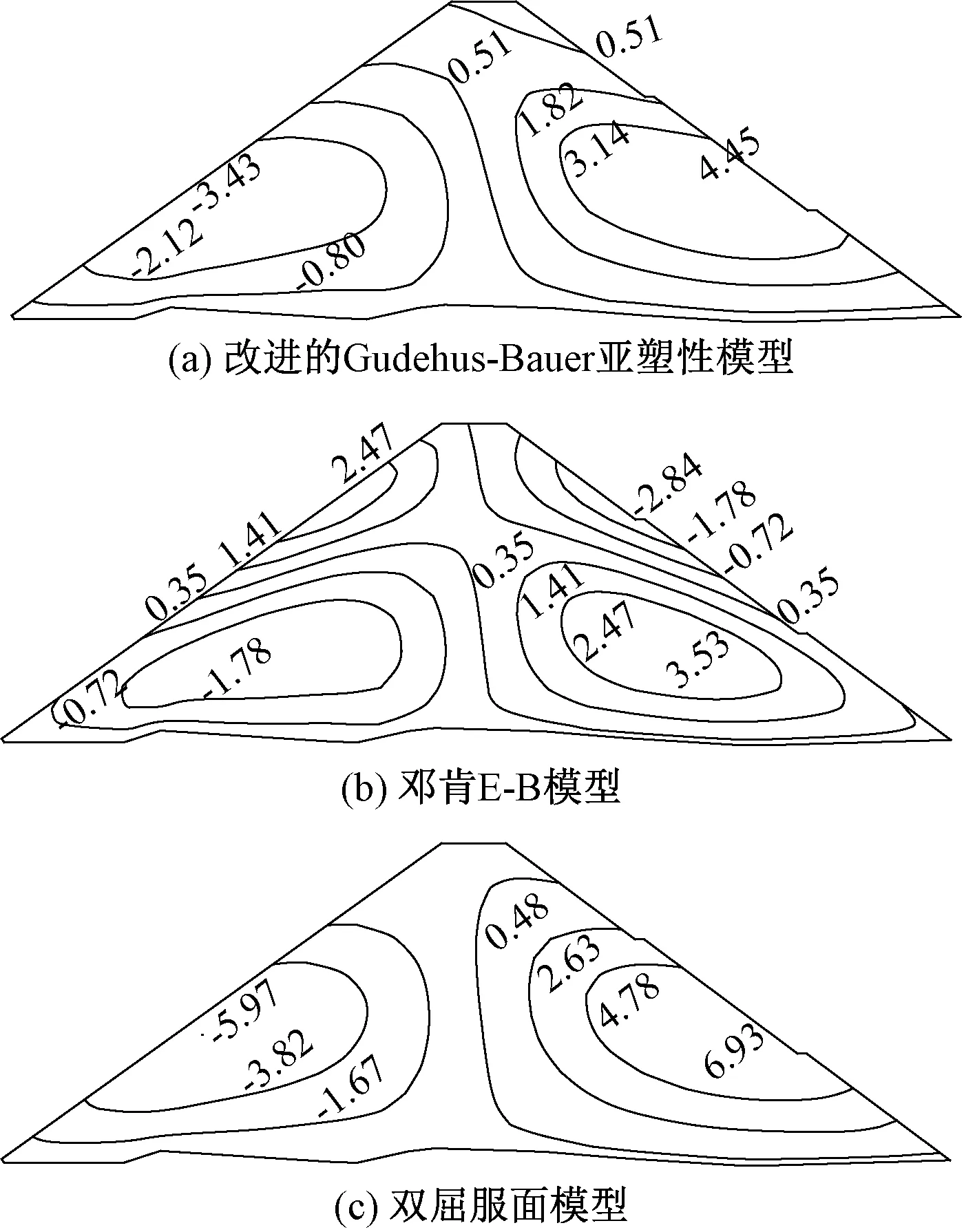
图5 竣工期水平位移(cm)Figure 5 The horizontal displacement in construction period(cm)

由图4可知，改进的Gudehus-Bauer亚塑性模型和双屈服面模型计算的沉降量相近，最大值分别为22.9 cm和24.0 cm，E-B模型的最大沉降量为32.1 cm。3种模型计算的坝体水平位移基本呈对称分布。

由图5可知，改进的Gudehus-Bauer亚塑性模型和双屈服面模型计算的水平位移分布规律相近。改进的Gudehus-Bauer亚塑性模型、邓肯E-B模型和双屈服面模型计算的最大上游向水平位移分别为3.43、2.84、5.97 cm，最大下游向水平位移分别为4.45、3.53、6.93 cm。

蓄水期的坝体沉降量和水平位移如图6和图7所示。

图6 蓄水期沉降量(cm)Figure 6 The vertical displacement in storage period(cm)

图7 蓄水期水平位移(cm)Figure 7 The horizontal displacement in storage period(cm)

由图6可知，蓄水期坝体的沉降量明显有所增大。改进的Gudehus-Bauer亚塑性模型、双屈服面模型和邓肯E-B模型的最大沉降量分别为26.4、26.5、34.8 cm，比竣工期增加3.5、2.5、2.7 cm，约占坝高的0.35%、0.35%和0.46%。

由图7可知，改进的Gudehus-Bauer亚塑性模型和双屈服面模型计算的蓄水期坝体水平位移相近，最大上游向位移分别为1.41 cm、2.98 cm，最大下游向位移为5.31 cm、7.92 cm。E-B模型计算的水平位移发生较大变化，蓄水期产生上游的位移基本消失。

3.4 蓄水期面板应力变形分析

蓄水期面板挠度分布规律，如图8所示。

图8 蓄水期面板挠度Figure 8 Deflection of face slabs

由图8可知，蓄水期面板在水压力作用下产生明显的下游向位移，分布规律为：面板的最大挠度出现在河谷段面板下部约1/3坝高处，且挠度值向四周逐渐减小；改进的Gudehus-Bauer亚塑性模型与双屈服面模型计算的最大挠度较为接近，分别为0.094 m和0.078 m；而邓肯E-B模型的计算值偏大，最大为0.138 m。

蓄水期面板坝轴线向位移，如图9所示。由如图9可知，面板的总体趋势是岸坡段面板向河床位移，3种模型计算的面板最大坝轴线向位移较为接近，改进的Gudehus-Bauer亚塑性模型、邓肯E-B模型和双屈服面模型计算的最大左岸向位移分别为0.017、0.015、0.011 cm，最大右岸向位移分别为1.6、1.4、1.0 cm。

由图10可知，3种模型计算的蓄水期河床段附近的面板中部顺坡向主要承受压应力。改进的Gudehus-Bauer亚塑性模型和双屈服面模型计算的面板底部和顶部顺坡向处于受拉状态，最大值分别为0.1、0.2 MPa，远小于邓肯E-B模型面板底部顺坡向最大拉应力。邓肯E-B模型计算的面板底部顺坡向基本上都处于受拉状态，最大拉应力为1.70 MPa，出现在河床段面板底部。

图9 面板轴线向位移Figure 9 Axial displacement of face slabs

图10 面板顺坡向应力Figure 10 Stress along slop direction of face slabs

由如图11可知，蓄水期河床段面板中下部承担了最大的轴线向压应力，改进的Gudehus-Bauer亚塑性模型、邓肯E-B模型和双屈服面模型计算的最大坝轴线向压应力分别为2.24、3.60、1.68 MPa，面板坝轴线向基本上处于受拉状态，但拉应力不大，分别为0.49、0.69、0.40 MPa。

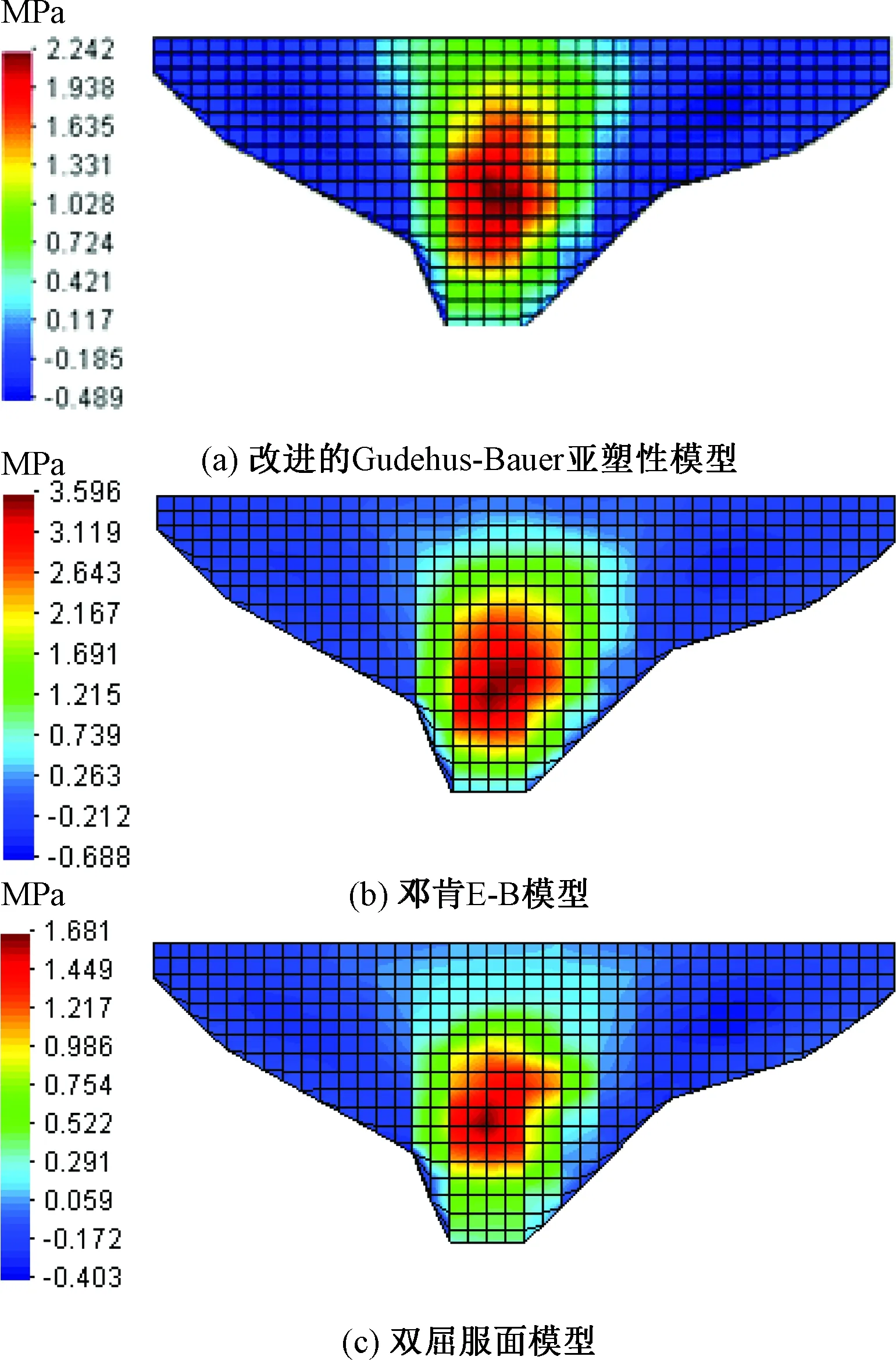
图11 面板轴线向应力Figure 11 Axial stress of face slab

4 结论

根据改进的堆石料Gudehus-Bauer亚塑性本构模型，将其应用于面板堆石坝的应力变形分析，得到如下结论：

(1)改进的Gudehus-Bauer亚塑性模型计算的堆石体沉降量、水平位移以及坝体的主应力等主要结果与沈珠江双屈服面模型的计算结果较为接近。

(2)改进的Gudehus-Bauer亚塑性模型计算的蓄水期面板应力和变形分布规律与沈珠江双屈服面模型和邓肯E-B模型基本一致，且克服了蓄水期邓肯E-B模型面板底部顺坡向拉应力偏大的缺点。因此，改进的Gudehus-Bauer亚塑性模型为堆石坝数值计算提供了参考。