地籍图中线状要素自动综合研究

杨曦承

摘  要：由于地籍图数据量和应用范围的不同，具有多个不同比例尺成图形式。本文提出了一种基于多比例尺地图数据综合线要素的方法，来满足此类图中道路等线状要素连续综合的要求，此方法在不同比例尺的线性要素上标识共同的点，将大型道路等要素划分为多个线段，对每个线段的统一阈值采用DP算法，获得结果最终综合。结果表明，该方法可以获得更接近真实现状的线要素结果。

关键词：地籍图  线要素  DP算法  不同比例尺  地图综合

中图分类号：P208                             文献标识码：A                 文章编号：1674-098X（2020）09（b）-0031-03

Absrtact： Due to the difference of cadastral map data and application scope， there are many different scale mapping forms. In this paper， a method of synthesizing line elements based on multi-scale map data is proposed to meet the requirements of continuous synthesis of linear elements such as roads in this kind of map. This method marks common points on linear elements of different scales， divides large-scale road and other elements into multiple line segments， and adopts DP algorithm for the unified threshold of each line segment to obtain the final synthesis. The results show that the method can get the line element results closer to the real situation.

Key Words： Cadastral map;  Linear element;  DP algorithm;  Different scale;  Map synthesis

當前的地籍图和地籍数据信息系统已用于日常工作和自然资源管理中。众所周知，根据地籍数据大小、应用程序使用差异和区域差异，地籍图可以使用1：50，000、1：10，000、1：5，000和其他比例尺[1]。在不同比例的地籍地图中，它经常涉及边缘、对比度和调整。地图要素的自动综合是地籍制图的困难之一，当地籍地图用户在手机、计算机等的屏幕上执行各种操作时，他们希望地籍地图能够根据其需求进行更改并保持其视图，这对连续地籍地图的自动合成提出了更高的要求。地图综合的传统方法是根据特定比例尺数据生成客观比例尺数据[2]。假设当前的地籍地图管理系统数据库以多个比例尺存储地图数据，则可以使用多个比例尺的地籍地图数据生成中间比例尺地图数据。与基于单比例尺数据的综合相比，基于多比例尺地籍图数据的综合显然应导致更完整的结果，反映出现实情况[3]。

地籍图中的大多数数据都是线性特征，从某种意义上说，这些多边形所描述的多边形也可以被认为是闭合曲线，因此作者将重点介绍如何处理地籍图中的线性特征。如道路等多种规模的数据综合方法[4]。目前，主要的线要素合成方法包括Douglas_Peucker方法，基于Li和Openshaw的自然方法的方法以及基于Aitinghua偏差的方法。集成的Douglas_Peucker算法（以下称为DP算法）是一种改进的垂直距离方法算法，继承了垂直距离方法的优点，并且效率更高[5]。这是一种更好的数据压缩方法，具有广泛的应用范围，尤其是连续曲线效果很好。因此，作者结合Douglas_Peucker综合算法，提出了一种基于多尺度数据的线性要素综合方法[6]。

1  地籍图线状要素多比例尺自动综合

多比例尺线状要素综合方法的思想是，如果在两个不同地籍图的线要素中存在一个相同的点，则还必须保留在平均比例的线要素中。传统的线要素综合方法无法保证。为了有效地在对应于不同比例尺地籍图的线要素中保留这样相应的点，必须标识具有相同名称的点。在获得具有相同名称的点之后，可以使用DP算法基于保留具有相同名称的点来综合线状要素，以获得目标比例尺的线要素。

1.1 Douglas_Peucker算法

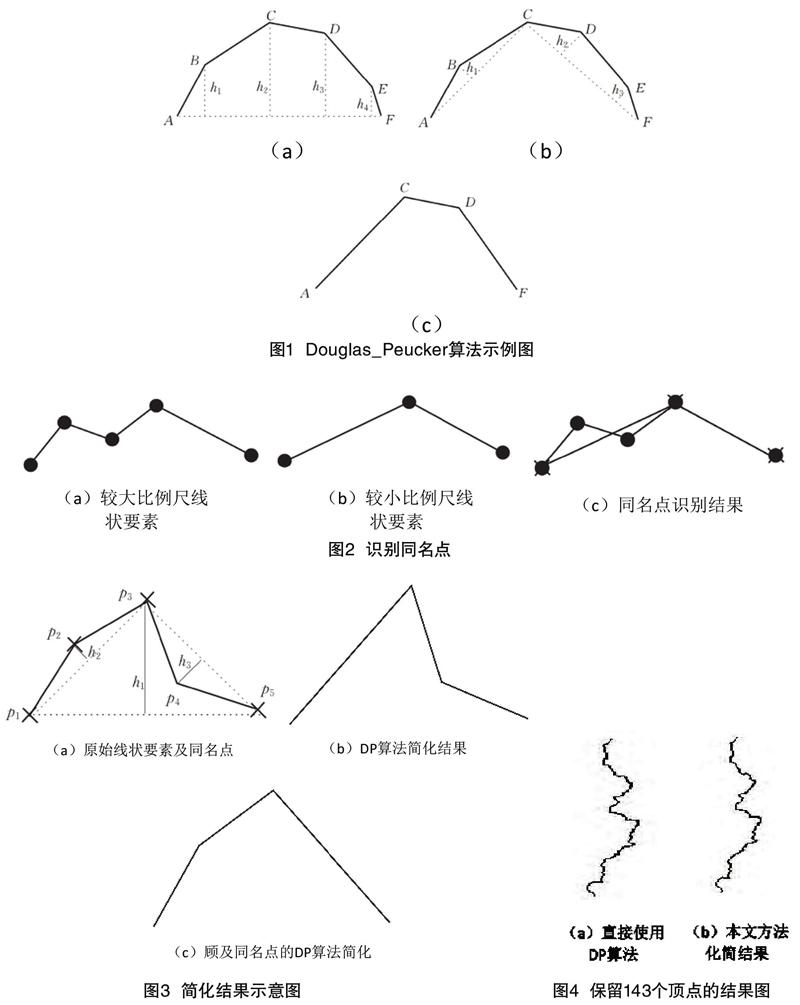
Douglas_Peucker算法是公认的线要素简化经典算法。其描述如图1所示。

首先将曲线首尾两点A、F连接成一条直线AF，计算其余各点到直线AF的距离，选择距离最大值的与阈值比较，若大于阈值，则保留该点（图中点C），否则删除掉直线AF两端点间的其他点，然后以该点分界将曲线分为两部分AC和CF，各部分仍然选择距离最大值和阈值比较，决定取舍，以此类推，直到无点可舍为止，如图1（c）所示。优点是具有平移以及旋转不变性。

1.2 多比例尺线状要素综合方法

在不同比例地籍图的线要素上具有相同名称的点本质上是具有相同坐标的，可以使用点的坐标来匹配相同名称的点。考虑到绘图过程、方法不一致，具有相同名称的点的坐标可能并不完全一致，当匹配有相同名称的点时，点缓冲区将用作重合的基础。具体步骤是：首先，以每个点为圆心绘制一个半径为r的圆，r取值具体取决于线要素本身的特定点精度条件;然后对于具有不同比例的每个线要素，点缓冲区圆执行相交操作。如果两个圆的交点不为空（即两个圆具有重叠的区域），则可以将两个对应的顶点视为相同的名称点，如图2所示。在具有较大比例尺的线要素上标记具有相同名称的点标记。此时，标记的点是在较小比例的线要素上也存在的点，综合时必须保留。

在确定了具有相同名称的特征点之后，我们将使用经典的DP算法基于保留相同名称的点来大规模综合线要素。如何有效保留相同名称的点是本文方法的关键。策略是采用标记有与断点相同名称的点，将原始线性特征分成多个线段，然后在具有统一阈值参数的这些多个线段上运行DP算法。这不仅确保在综合过程中不会删除具有相同名称的特征点，而且还有效地使用了DP算法。

图3显示了此方法和经典DP算法的组合结果。其中，具有相同名称的点用“×”表示。图3（b）和3（c）显示了两种方法保留4个顶点时的组合结果。

如图3所示，经典的DP算法将删除h2中具有最小垂直距离的同名点p2，然而p2是此线状要素的一个重要特征点。但是，本文中的方法有效地维护了具有相同名称的点，并以更大的垂直距离移除了h3处的顶点p4，保留了p2。

2  实验

在这里，作者使用某地籍资料中同一国道上不同比例尺，分别为1：10000，1：50000，1：100000比例尺图上的道路要素进行比较分析。使用形式相似度SS来表现实验结果与原始数据之间的相似度。转向函数用于识别线状要素的形状。为了减少小干扰对单元边界和单元形状及原始形状的影响，应进行匹配。通过匹配，两个转向函数非重叠区域的面积用表示，对象i在两张图上的同一区域用Oi表示。两个道路要素形状的绝对差别为，对象在地籍图 A 和地籍图 B 上的 SS 值由式（1）计算：

式中，为转向函数折线下方的面积。两个对象经过比较，如果是相同的，那么转向函数也是相同的，SS 的结果为 1。每个道路要素在地籍图 A 与其在地籍图 B 上的相应形状之间都产生一个 SS 值。地籍图A 与地籍图B 的相似度确定为每个 SS 值之和的平均值，如式（2）：

图4为使用DP算法和本文中的方法保留若干个相同点的综合结果。在计算SS指数时，直接使用DP算法的综合结果与1：5万比例尺数据的相似度为0.9238，而该方法的综合结果与1：5万比例尺数据的相似度为0.9294。可以看出，该方法在本文中的综合结果更加接近于真实数据，更能反映真实的道路特征。

3  结语

地籍图制作和使用中，道路等线状要素作为比较复杂的地物，与其周边其他地物产生非常广泛的联系，在管理中具有较强的制图综合的需求。本文中作者提出了一種基于多比例尺地籍图数据中道路等线状要素合成方法来实现这种需求。使用不同比例尺的地籍图数据，在线状要素上标识相同的特征点。然后，使用这些标记点，把大型线要素划分为多个线段。最后，根据分割后各段的统一阈值进行DP算法，最终得到自动综合的结果。通过比较实验结果得出结论，该方法在保留地籍图上相同名称的特征点的基础上，获得的线要素的综合结果更加接近现实状态。

参考文献

[1] 周芳.地图综合中传输的信息及其关系探讨[J].智能城市， 2020（2）：11-14.

[2] 杨锐波.地图线状要素编辑处理方法综合研究[J].科技创新导报， 2019（8）：45-47.

[3] 禄小敏.顾及权重信息的地图点群目标自动综合方法[D].兰州：兰州交通大学，2019.

[4] 李伟.地图综合中曲线局部尖锐凸角的光滑方法[J].测绘科学，2018（4）： 112-116.

[5] 郭沛沛.道路网约束下城市大比例尺地图上的建筑物和兴趣点综合方法[D].青岛：山东科技大学，2017.

[6] 王荣林.区域综合航海地图集设计与编制[J].中国海事，2019（5）：53-55.