Reverse Indices and Polynomials of (Propyl) Ether Imine PETIM Dendrimer

MUHAMMAD Jamil，IFTIKHAR Ahmed，HASEEB Ahmad

(1.Department of Mathematics，Minhaj University，Lahore，Pakistan 54000；2.Department of Mathematics，Riphah International University，Lahore，Pakistan 54000；3.Department of Mathematics，Lahore Leads University，Lahore，Pakistan 54000)

Abstract: Dendrimers that are useful in medications are important structures research. To understand the properties of dendrimers is an important task. it is almost impossible to study properties of dendrimers in lab due to the limits of experimental conditions. But Topological indices provide help so researchers can predict properties of dendrimers without performing experiments. In this paper, we study one of the most important dendrimer structure namely (propyl) Ether Imine PETIM dendrimer and compute several reverse indices and first and second reverse Zagreb polynomials for (propyl) Ether Imine PETIM dendrimer.

Key words: dendrimer；topological index；Zagreb polynomial；Zagreb index

The research field in which graph theoretical techniques are used to solve the problems of chemistry is known as chemical graph theory. In these studies we associate numbers with the molecular graphs of chemical compounds that remains invariant upto graph isomorphism and are called topological indices (TIs). TIs help us in guessing the properties of concerned chemical compound without performing experiments in the wet lab. An important field of research is Cheminformatics in which QSAR and QSPR together with TIs are used to know about the properties of different chemical structures[1-3].

In recent years, many researchers defined and computed several TIs and correlate them with the properties of chemical compounds[4-5]and more than 150 TIs are present in literature. But the reality is, no single TI can give all properties of a chemical compound. Hence researchers are always interested to define new TIs, for example, reverse TIs, redefined Zagreb indices (ZIs), etc.

A graphGis connected, if all vertices ofGare connected with each other. The length of smallest path between any two vertices is call distance between them. The degree of a vertexvis the number of vertices that are at distance one fromv. Throughout this paper, we consider only simple connected graphs.

The aim of this paper is to compute several reverse degree-based indices and first and second reverse Zagreb polynomials for (propyl) Ether Imine PETIM dendrimer.

1 Definitions of Reverse Topological Indices

In this section, we give definitions of topological indices and polynomials．

Definition1(Reverse First ZI)

The reverse first ZI is defined as：

Definition2(Reverse Second ZI)

The reverse second ZI is defined as：

Definition3(Reverse First Hyper ZI)

The reverse first hyper ZI is defined as：

Definition4(Reverse Second Hyper ZI)

The reverse second hyper ZI is defined as：

Definition5(Reverse Second Modified ZI)

The reverse second modified ZI is defined as：

Definition6(Reverse Harmonic Index (HI))

The reverse HI is defined as：

Definition7(Reverse Inverse Sum-Index (ISI))

The reverse ISI is defined as：

Definition8(Reverse Augmented ZI)

The reverse augmented ZI is defined as：

Definition9(Reverse first Zagreb Polynomial)

The reverse first Zagreb polynomial is defined as：

Definition10(Reverse Second Zagreb Polynomial)

The reverse second Zagreb polynomial is defined as：

Definition11(Reverse first Multiplication ZI )

The reverse first multiplicative ZI is defined as：

Definition12(Reverse Second Multiplication ZI )

The reverse second multiplicative ZI is defined as：

Definition13(Reverse Randic Index)

The reverse Randic index is defined as：

Definition14(Reverse inverse Randic Index)

The reverse inverse Randic index is defined as：

Definition15(Reverse Symmetric division Index (SDI))

The reverse SDI is defined as：

Definition16(Reverse Atomic Bond Connectivity Index (ABC))

The reverse ABC is defiend as：

Definition17(Reverse Geometric Arithmatic Index (GA))

The reverse GA is defined as：

Definition18(Reverse Sum-connectivity Index (SCI))

The reverse SCI is defined as：

Definition19(Reverse Modified Randic Index)

The reverse modified Randic index is defined as：

Definition20(Reverse Arithmatic Geometric Index (AG))

The reverse AG is defined as：

Definition21(Reverse Shigehalli & Kanabur Indices)

The reverse Shigehalli & Kanabur indices are defined as：

Figure 1 Graph of (Propyl) Ether Imine PETIM Dendrimer

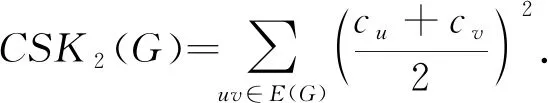
2 Main Results

In this section, we compute some reverse degree based topological indices of (propyl) Ether Imine PETIM dendrimer. Throughout this section,Gdenotes (propyl) Ether Imine PETIM dendrimer.

The molecular graphGis given in Figure 1.The edge partition ofGbased on the degree of end vertices is given in Table 1. The reverse degree based edge partition ofGis given in Table 2.

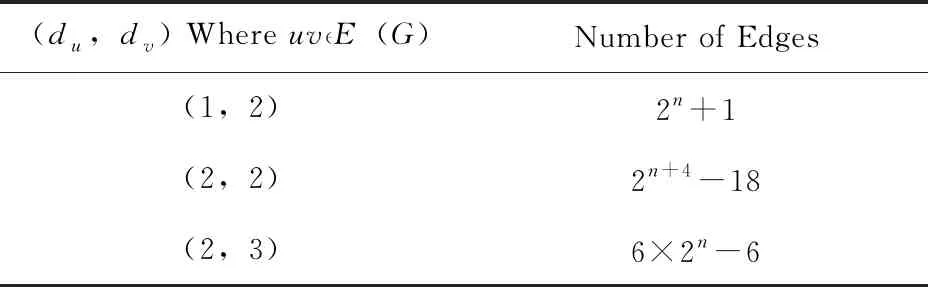
Table 1 Degree Based Edge Partition of G

Table 2 Reverse Degree Based Edge Division of G

Theorem1ForG, We haveCM1(G)= 46(2n+1)-24.

ProofBy definition of reverse first ZI, we have

=5|CE1(G)|+4|CE2(G)|+3|CE3(G)|

=5(2n+1)+4(2n+4-18)+3(6×2n-6)

=46(2n+1)-24.

Theorem2ForG, We haveCM2(G)= 44(2n+1)- 84.

ProofBy definition of reverse second ZI, we have

=6|CE1(G)|+4|CE2(G)|+1|CE3(G)|

=6(2n + 1) + 4(2n + 4-18)+1(6×2n-6)

=44(2n + 1)-84.

We skipped the proofs of the reaming theorem because they follow similarly as that of Theorem 1 and Theorem 2.

Theorem3ForG, We haveHCM1(G)=180(2n+1)-342.

Theorem4ForG, We haveHCM2(G)=176(2n+1)-312.

Theorem8ForG, We haveCA(G)= 96(2n+1-2).

Theorem9ForG, We haveCM1(G)= (x5+8x4+3x3)2n+1-18x4-6x3.

Theorem10ForG, We haveCM2(G)= (x6+8x4+3x2)2n+1-18x4-6x2.

Theorem11ForG, We haveCPM1(G)=52n+1×42n+4-18×36×2n-6.

Theorem12ForG, We haveCPM2(G)=62n+1×42n+4-18×26×2n-6.

Theorem14ForG, We haveCRRα(G)=(6α+8×4α+3×2α)2n+1-6×2α(3×2α-1).

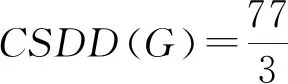
Theorem21ForG, We have

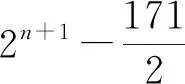
3 Conclusions

Dendrimers are artificial chemical structures that are buildup to manufacture new medicines. To avoid lab cast, TIs are used to know about different structural and chemical properties of dendrimers. In this paper, we presented several TIs and some polynomials for (propyl) Ether Imine PETIM dendrimer. Our results can help to understand the topology of concerned dendrimer structure and may help to enhance pharmaceutical industry.