两种吸附模型对阿特拉津在壤质砂土中的模拟效果分析

李晓宇，任仲宇，李芳春，井 琦*，魏明海

（1.北京工业大学建筑工程学院，北京 100124；2.水质科学与水环境恢复工程北京市重点实验室，北京 100124；3.同方知网（北京）技术有限公司，北京 100192；4.生态环境部环境规划院，北京 100012）

阿特拉津（Atrazine）是目前世界上广泛使用的除草剂之一，也是土壤和地下水中最常检测到的农药之一[1]，已在中国的松花江流域、辽河流域和长江流域中检测到[2-4]。阿特拉津被认定为有潜在的致癌作用并可影响人体的内分泌系统，美国、欧共体和日本等均把它列入内分泌干扰物名单[5-6]。阿特拉津及其代谢产物可在水和土壤中存在数十年[7]，其残留会对饮用水源和生态环境构成威胁，或通过食物链传递和生物富集作用对人体健康造成危害。因此，研究阿特拉津在多孔介质中的迁移与变化规律具有十分重要的现实意义。

国内外学者对影响阿特拉津迁移的主要过程（吸附与解吸）及作用机理的相关研究已有大量报道[8-9]。Kovaios等[10]研究了土壤对阿特拉津的吸附作用，发现阿特拉津的吸附是可逆的，并观察了吸附和解吸过程。针对土壤中阿特拉津的易迁移性，许多学者进行了室内土柱试验和田间试验，并在此基础上通过模型模拟阿特拉津的迁移，从而评价其对地下水的污染风险[4]。Mao等[11]、Zheng等[12]利用两点（两区）非平衡吸附模型模拟阿特拉津在土壤中的迁移，并取得了较好的模拟效果。Prata等[13]采用三点非平衡吸附模型成功地拟合了淋溶条件下阿特拉津在巴西一种氧化土中的穿透曲线。毛萌等[14]建立了包含吸附项和降解项的对流弥散方程，模拟室内滴灌施药条件下阿特拉津在土壤中的迁移。Van Genuchten等[15]发展了两点模型的控制方程，在原方程基础上增加了降解项。Gamerdinger等[16]应用带有降解项的两点模型模拟了室内定流速条件下阿特拉津在土柱中的迁移。

综上所述，已有研究对模型的改进主要表现在改进模型源汇项（例如考虑吸附、降解项等）或将两点非平衡吸附模型改进为三点非平衡吸附模型。单点非平衡吸附模型是两点非平衡吸附模型的特例[15]，Selim等[17]曾利用单点非平衡吸附模型模拟分析2，4-D除草剂在饱和及非饱和分层土壤中的迁移，但未讨论该模型的模拟效果。吸附-解吸模型可用来模拟病毒、细菌和胶体等在多孔介质中的迁移[18]，Yu等[19]还应用吸附-解吸模型模拟了纳米零价铁在饱和砂柱中的迁移，杜青青等[20]应用吸附-解吸模型模拟了氨氮在污染场地的迁移，但有关吸附-解吸模型模拟分析阿特拉津等农药在多孔介质中的迁移报道甚少。笔者在利用单点非平衡吸附模型模拟阿特拉津迁移过程中，发现在淋洗阶段误差较大，进而考虑采用吸附-解吸模型对阿特拉津迁移进行模拟，通过改进吸附、解吸的源汇项表达，以期消减此误差。

本文通过构建室内土柱阿特拉津动态迁移试验，获取模拟所需参数，利用HYDRUS-1D软件，分别建立了基于单点非平衡吸附模型和吸附-解吸模型的运移模型，采用整体调参和分段调参两种模拟方式，模拟阿特拉津在饱和壤质砂土中的迁移与分布规律，深入分析了两种模型模拟结果差异背后的物理机理，并对源汇项的分项逐项进行计算，定量分析了两种吸附模型对模拟结果的影响过程和影响程度，可为深刻认识阿特拉津的迁移特征及其环境风险评价提供科学依据。

1 材料与方法

1.1 室内土柱试验

1.1.1 材料与仪器

试验材料：阿特拉津（纯度98%，国家标准物质中心）、氯化钾（分析纯，北京化工厂）、甲醇（色谱纯、国药集团化学试剂有限公司）。供试土壤采自北京市永定河河滩，采样深度40 cm，土壤取回后自然风干，过2 mm筛备用。用简易比重计法进行了该土壤的粒径分析，并按国际制将土壤质地定名为壤质砂土。分析土壤的砂粒含量为86.653%，粉粒含量为11.795%，黏粒含量为1.553%，有机质含量为4.230%，干容重为1.656 g·cm-3，有效孔隙度为0.130，pH值为6.300。

试验仪器：电子天平（JA2003，上海恒平科学仪器有限公司）、电导率仪（sensION5，哈希水质分析仪器有限公司）、高效液相色谱仪（Agilent1100，安捷伦科技有限公司）等。

模拟装置如图1所示，由进水装置、土柱主体、出水装置三部分组成。进水装置由马氏瓶、进水管和升降支架组成，马氏瓶用于维持土柱定水头淹水状态，升降支架用于承载马氏瓶，可调节高度。土柱主体由有机玻璃柱和充填介质组成，有机玻璃柱工作长度36 cm，内径6 cm，柱顶设置溢流孔，柱中及柱底分别设置取样孔。出水装置由出水管和集液箱组成。

图1 柱试验装置示意图Figure 1 Schematic diagramof column experimental device

1.1.2 土柱迁移试验

在土柱底部铺设5 cm厚粒径为0.5～2 cm的卵砾石，然后将风干过筛后的土壤按10 cm层厚分层填入土柱，装填过程中对土壤层间打毛并在表层土壤上部铺设3 cm厚粒径为0.5～2 cm的卵砾石。土柱填装完成后对土柱进行排气饱和并调整进水出水的水位差，得到稳定渗流速度，在维持水位差恒定条件下将浓度为22µg·mL-1的阿特拉津渗滤液从顶端注入柱内,注入时长200 min，总注入水量1650 cm3，约12.5个土壤有效孔隙体积（12.5 PV），注入结束后瞬时用去离子水淋洗土柱,淋洗时间150 min，总淋洗水量1238 cm3（9.4 PV）。定时从取样孔取样，并测定渗流液中阿特拉津浓度。每次每个观测孔取样2个，测定结果取样品的平均值。

1.1.3 测定方法

应用安捷伦高效液相色谱仪测定阿特拉津浓度。试验采用C18色谱柱，设置流动相（甲醇∶水=70∶30）的流速为1 mL·min-1，在225 nm波长条件下用UVVIS检测器测定。通过比对峰面积/浓度标线，计算得到不同时刻阿特拉津浓度。

1.2 模型的建立

HYDRUS软件可用于模拟分析非饱和、饱和多孔介质中的水和溶质运移[18]。本文利用HYDRUS-1D软件建立土壤水流和溶质运移数值模型，模拟阿特拉津溶液入渗进入饱和土柱后的迁移过程以及随后淋洗条件下阿特拉津在饱和土柱中的迁移过程，设定时间单位为min，质量单位为µg，长度单位为cm。根据土柱试验的运行情况，将模拟时长定为350 min。

1.2.1 水流模型的基本方程

一维平衡水流运动采用Richards方程来描述[18,21]：

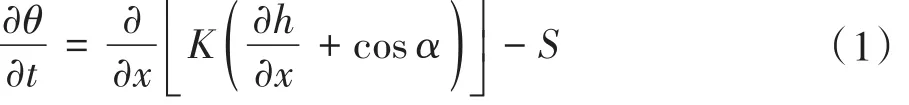
式中：h为土壤压力水头，cm；θ为土壤体积含水率；t为时间，min；S为源汇项，min-1；α为水流方向与垂直方向夹角（即：α=0°代表垂向流动，90°代表水平流动，0°＜α＜90°代表倾斜流）；x为空间位置，cm；K为非饱和水力传导度函数，cm·min-1，如式（2）：

式中：Kr为相对水力传导度；Ks为饱和水力传导度，cm·min-1。

本研究水流模型概化为均质各项同性饱和一维垂向稳定流，因此方程（1）可简化为下式：

式中各参数意义同上。

1.2.2 水流模型的初始条件及边界条件

模型初始条件为整体饱和状态，即初始含水率为饱和含水率。

模型上边界为供水边界，下边界为排水边界，且均为定水头边界，水头差为5.17 cm，通过插值得到土柱内的初始流场。

1.2.3 溶质迁移模型的基本方程

通过改进的对流弥散方程来模拟阿特拉津在饱和多孔介质中的迁移，该方程[22]用一个源汇项表示阿特拉津与固体基质的反应（吸附和解吸过程）。

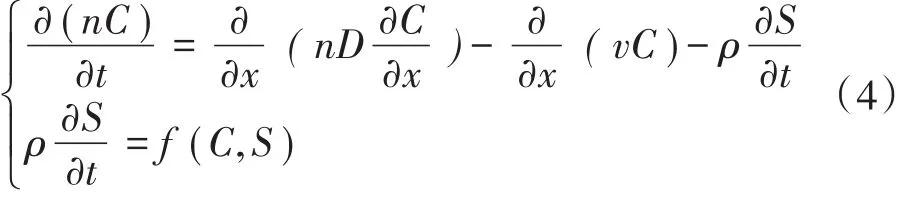
式中：n为孔隙度；C为溶质浓度，µg·mL-1；S为多孔介质中溶质固相浓度，µg·g-1；D为弥散系数，cm2·min-1；v为达西速度，cm·min-1；x为空间位置，cm；ρ为多孔介质干容重，g·cm-3；t为时间，min。

根据不同的吸附机理，源汇项方程式有不同的表达形式。本文分别采用单点非平衡吸附模型和吸附-解吸模型对比模拟分析阿特拉津在土柱中的迁移过程。

式中：α是一级反应物质交换率系数（表示单位时间液相与固相间溶质质量转化大小），min-1；Kd是Henry线性吸附系数，mL·g-1。

式中：ka为吸附系数,min-1；kb为解吸系数,min-1；ψ 为溶质吸附函数；Smax是固相最大吸附量，µg·g-1；θ为土壤体积含水率，在饱和状态下，砂土中θ可近似认为等于孔隙度。

1.2.4 溶质迁移模型的初始条件及边界条件

模型初始条件为初始时刻土柱各位置溶质浓度为0。

模型上边界为浓度通量边界，下边界设定0梯度边界条件。佩克莱数Pe表示对流与扩散在溶质迁移中所占比例[24]。Parlange等[25]认为，当Pe＞4时，近似认为多孔介质流体中溶质浓度与某时段内按出流量计算的平均溶质浓度相等，此时边界条件为0浓度梯度边界条件。Pe计算公式如下：

式中：L为柱长，cm；u为实际平均速度，u=v/n，cm·min-1；D为弥散系数，cm2·min-1。通过计算本试验佩克莱数Pe=49.860＞4，符合Parlange等[25]研究的判定条件，即扩散作用相对于对流作用在溶质迁移中所占的比例较小，此时出流溶质的浓度梯度近似为0，故下边界设定为零梯度边界。

1.3 模型参数的获取

本模拟中需要的参数有土壤水力特征参数和溶质特征参数，土壤特征参数主要指孔隙度、饱和渗透系数等；溶质特征参数主要指弥散系数、吸附系数等。

1.3.1 土壤水力特征参数

土壤水力特性参数的准确性对于反映实际土壤水分运动过程具有重要意义[26]。本研究采用常水头法测定土壤介质饱和渗透系数Ks，容积排水法测定土壤介质孔隙度。测量结果土壤饱和渗透系数为0.340 cm·min-1，孔隙度为0.349。

1.3.2 弥散系数

弥散系数是表征可溶性物质通过渗透介质时弥散现象强弱的指标，可通过实验利用投加示踪剂测定其穿透曲线的方式获取。本研究在室内土柱模拟装置中，以Cl-作为示踪剂，在饱和一维稳定流条件下淋滤KCl溶液，并在土柱出口端定时测定Cl-浓度,利用公式（8）[27]计算弥散系数。计算得到弥散系数为0.600 cm2·min-1。

弥散系数计算表达式：

式中：t0.16、t0.5、t0.84为柱中一个固定点x处相对浓度，分别为0.16、0.5、0.84时对应的时间，min。

Cl-浓度测试采用电导率法。配制不同浓度的KCl溶液，并测定其对应的电导率值，绘制电导率与KCl浓度的关系曲线，试验时用电导率仪测定样品电导率，利用电导率与KCl浓度关系将电导率换算为浓度。

1.3.3 等温吸附系数

吸附系数的确定由室内吸附试验获得，本研究中阿特拉津在土壤中的吸附行为符合Henry等温线性吸附，线性吸附系数Kd为0.372 mL·g-1；将土壤在浓度为22µg·mL-1的阿特拉津溶液中恒温振荡200 min，得到吸附量为6.450µg·g-1，以此作为本试验条件下的固相最大吸附量Smax。

2 结果与讨论

2.1 模型参数率定

在水力试验基础上确定水流模型参数，建立土柱一维水流稳定流模型，调整边界水头以改变土柱内的流场，将观测孔的实测测压管水头值和计算水头值进行对比，反复进行三次，取误差较小的情形所对应的参数为模型水流参数。模型中涉及的土壤水力特征参数如饱和渗透系数为0.340 cm·min-1，孔隙度为0.349。

水质模型中源汇项涉及的参数有弥散系数D、一级反应物质交换率系数α、线性吸附常数kd、吸附系数ka、解吸系数kb、固相最大吸附量Smax。弥散系数D、线性吸附常数kd、固相最大吸附量Smax通过实验得到，并在模型中适当调整，最终得到这些参数值：D为0.600 cm2·min-1，kd为0.372 mL·g-1，Smax为6.450 µg·g-1；针对以上两种吸附模型中不易通过试验直接测得的参数如一级反应物质交换率系数α、吸附系数ka、解吸系数kb进行调参，得到综合反映整个试验过程的“平均的”α、ka和kb，分别为 0.200、0.179 min-1和 0.126×10-5min-1。

实际情况下，随注入、淋洗阶段时间的增长，模型中的一级反应物质交换率系数、吸附和解吸系数会发生变化。为了探究实际情况下各反应系数的变化过程及对模拟效果的影响，本研究以观测孔1和观测孔2为调参检验点，结合阿特拉津穿透曲线形态，将模拟按照穿透曲线的“上升段”“峰值段”“下降段”分段进行调参模拟，得到各阶段参数值如表1所示。

2.2 模拟结果

图2、图3分别为取样孔1和取样孔2阿特拉津浓度实测值与整体调参（未分段调参）拟合的单点非平衡吸附模型、吸附-解吸模型模拟计算结果对比图。图4、图5分别为取样孔1和取样孔2阿特拉津浓度实测值与分段调参拟合的单点非平衡吸附模型、吸附-解吸模型模拟计算结果对比图。

单点非平衡吸附模型在阿特拉津注入过程中拟合情况较好，各观测点浓度模拟值和实测值较为一致，但在淋洗过程中，模拟结果相比于试验结果有较为明显的误差，不能较好地重现整个过程（见图2和图3）；吸附-解吸模型在整个过程中模拟值与实测值趋势更为一致，且误差较小，可以较好地描述阿特拉津在土壤中的迁移过程。通过观察图4、图5并与图2、图3对比可知，分段调参拟合的单点非平衡吸附模型的拟合度在注入阶段提升不明显，在淋洗阶段有显著提升；分段调参拟合的吸附-解吸模型的拟合度在注入阶段和淋洗阶段均提升很小。

2.3 模型结果检验

选用Nash-Suttcliffe模拟效果系数（NSC）和均方根误差（RMSE）评价模型计算结果，计算公式分别为：

表1 各阶段一级反应物质交换率系数、吸附和解吸系数拟合值Table 1 Fitting values of exchange rate coefficient of first order reactive substance，adsorption and desorption coefficients at each stage

图2 观测孔1整体调参拟合：单点非平衡吸附模型与吸附-解吸模型模拟结果对比图Figure 2 Integral parameter fitting of observation hole 1:The simulation result compartion chart of one-site non-equilibriumadsorption model and adsorption-desorption model

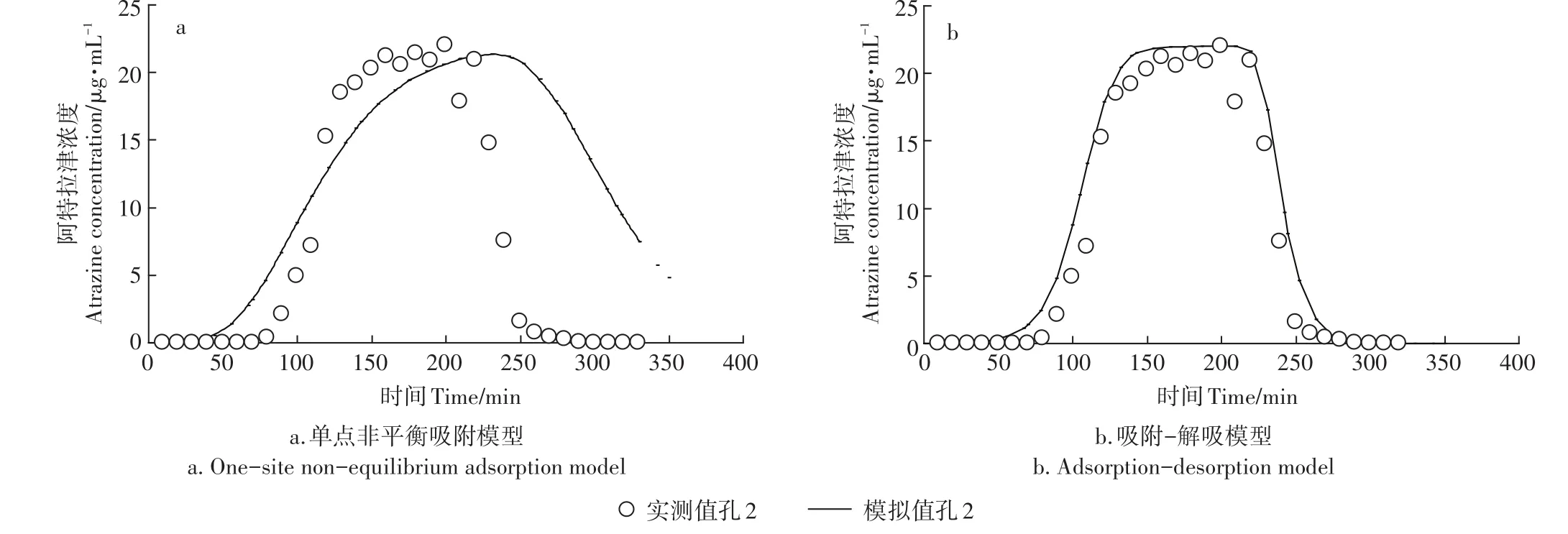
图3 观测孔2整体调参拟合：单点非平衡吸附模型与吸附-解吸模型模拟结果对比图Figure 3 Integral parameter fitting of observation hole 2:The simulation result compartion chart of one-site non-equilibriumadsorption model and adsorption-desorption model

图4 观测孔1分段调参拟合：单点非平衡吸附模型与吸附-解吸模型模拟结果对比图Figure 4 Segmental parameter fitting of observation hole 1:The simulation result compartion chart of one-site non-equilibriumadsorption model and adsorption-desorption model

式中：Xobs为实测值，Xmodel为模型计算值，Xˉobs为实测值的算术平均值。当模型计算值和实际监测值相等时，NSC=1，模拟效果最好；通常NSC在0～1之间，NSC越大，说明计算值与观测值匹配程度越好，一般当NSC＞0.75时，表示模拟结果可以接受。

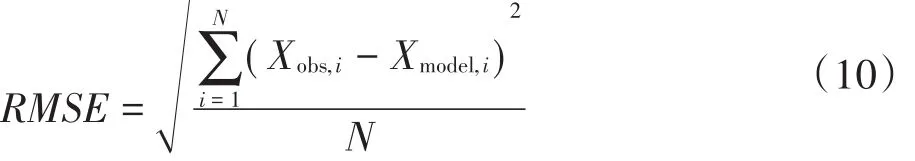
式中：N表示实测值个数，Xobs,i和Xmodel,i为试验观测值与模型计算值。RMSE越小，说明计算值与观测值匹配程度越好。

分整体调参拟合和分段调参拟合两种情形，按照阿特拉津注入阶段、淋洗阶段和注入-淋洗全阶段，计算单点非平衡吸附模型和吸附-解吸模型的NSC和RMSE值，如表2所示。

由表2可知，整体调参拟合情形下，单点非平衡吸附模型模拟注入阶段（吸附阶段）NSCs与RMSEs分别为0.909～0.922和2.752～3.167，吻合较好；而对于淋洗阶段，NSCs为负，说明拟合度很低；单点非平衡吸附模型模拟阿特拉津注入-淋洗的全过程的NSCs与RMSEs分别为0.138～0.593和6.180～8.395。分段调参拟合后，注入阶段的NSCs提高到0.919～0.941，RMSEs减小到2.405～2.986，淋洗阶段的NSCs提高到0.927～0.940，RMSEs减小到2.309～2.036，注入-淋洗全阶段的NSCs提高到 0.921～0.941，RMSEs减小到 2.204～2.717。说明用分段拟合的单相非平衡吸附模型模拟阿特拉津注入、淋洗和注入-淋洗的全过程均是适宜的。

同样通过观察吸附-解吸模型的孔1和孔2的NSC和RMSE值可知，无论整体调参模拟和分段调参模拟，吸附-解吸模型模拟阿特拉津注入、淋洗和注入-淋洗全过程均是较为适宜的。分段拟合的吸附-解吸模型模拟阿特拉津注入、注入-淋洗全过程的模拟效果系数有微弱提高。

2.4 两种模型机理对比分析

图5 观测孔2分段调参拟合：单点非平衡吸附模型与吸附-解吸模型模拟结果对比图Figure 5 Segmental parameter fitting of observation hole 2:The simulation result compartion chart of one-site non-equilibrium adsorption model and adsorption-desorption model

单点非平衡吸附模型认为固相中的吸附量S与一级反应物质交换率系数α和线性吸附常数与溶质液相浓度的乘积KdC有关。S和KdC随着吸附过程的发生不断发生变化。根据单点非平衡吸附模型，可将阿特拉津在土柱中的迁移、吸附过程描述如下：初始时刻柱中各位置阿特拉津固相及液相浓度均为0，阿特拉津随水流迁移进入土柱，土柱中液相浓度升高，同时发生吸附作用，固相浓度随之增加，达到吸附平衡后停止吸附。随后，注入去离子水，吸附在固相中的阿特拉津逐渐解吸到水中随水流出。由图2、图3可知，阿特拉津连续注入阶段（吸附阶段）模拟值与实测值偏差较小，但在去离子水注入阶段（淋洗阶段）则偏差很大。这是因为整个注入-淋洗阶段的一级反应物质交换率系数α为同一常数，淋洗阶段由于采用了与注入阶段相同的α，导致淋洗阶段实测值与模拟值差异较大。分段拟合后，单点非平衡吸附模型由于在注入阶段和淋洗阶段采用了与对应阶段相匹配的α，因此注入阶段和淋洗阶段的拟合度均较高。

表2 各阶段模型模拟效果系数（NSC）和均方根误差（RMSE）值Table 2 Simulation effect coefficient（NSC）and root-mean-squared error（RMSE）values of models at each stage

为了进一步说明两种吸附模型的结果差异，本文对两种吸附模型在不同阶段的源汇项值进行了准确计算，分别列示于表3与表4。

表3列出了观测孔1单点非平衡吸附模型源汇项计算值。由表3可知：随着阿特拉津溶液的持续注入，模型计算得到的液相浓度和固相浓度逐渐增大，均为正值且逐渐减小，到阿特拉津注为0.003 µg·cm-3·min-1，此时固相浓度仍有较小的正向增长；在淋洗阶段，随着去离子水的持续注入，模型计算得到的液相浓度和固相浓变为负值（负值表示解吸过程）且绝对值与注入阿特拉津时的源汇项值相近，即吸附到固相中的阿特拉津逐渐解吸到溶液中，解吸速率与注入阿特拉津溶液时的吸附速率大致相当，因此采用单点非平衡吸附模型在淋洗阶段模拟值远超出实测值。

吸附-解吸模型认为吸附和解吸速率不同，将模型分为吸附项和解吸项分别描述，用ka和kb代表吸附和解吸的速率。在吸附项中，吸附量与溶质液相浓度C和最大固相浓度Smax有关，当吸附量达到Smax时停止吸附。根据吸附-解吸模型，可将阿特拉津在土柱中迁移、吸附过程描述如下：初始时刻柱中各位置阿特拉津液相和固相浓度均为0，随着阿特拉津注入土柱，土柱中液相浓度升高，同时发生吸附作用，固相浓度随之增加，随着土柱中各位置吸附量达到最大值后，吸附不再发生，整个过程中阿特拉津也会发生少量的解吸；对于淋洗阶段，同样存在着吸附和解吸作用，解吸系数kb在数值上很小，说明吸附到壤质砂土中的阿特拉津解吸速率很慢，这也是吸附-解吸模型计算值远低于单点非平衡模型计算值的原因。

表4列出了观测孔1吸附-解吸模型源汇项计算值。由表4可知：随着阿特拉津溶液的持续注入，模型计算的液相浓度和固相浓度逐渐增大，分别达到注入浓度和固相最大吸附量后维持不变，源汇项随着固相浓度的持续增大逐渐减小，达到最大固相吸附量后变成负值且维持恒定，此时的源汇项为-1.388×10-5µg·cm-3·min-1，可知固相浓度虽然在逐渐降低，但下降速率近似为0；在淋洗阶段，随着去离子水的持续注入，模型计算的液相浓度逐渐降低，源汇项为-1.388×10-5µg·cm-3·min-1，表明吸附在固相上的阿特拉津解吸速率极慢。通过观察阿特拉津液相浓度实测穿透曲线发现没有拖尾现象，也说明了其实际解吸速率很小。对比表3、表4的源汇项值计算结果，在解吸阶段单点非平衡吸附模型的源汇项计算值比吸附-解吸模型的源汇项计算值高出4个数量级，这是引起两种模型计算结果差异较大的原因。

表3 观测孔1单点非平衡吸附模型源汇项计算值Table 3 Calculation values of source and sink terms of the onesite non-equilibriumadsorption model of the observation hole 1

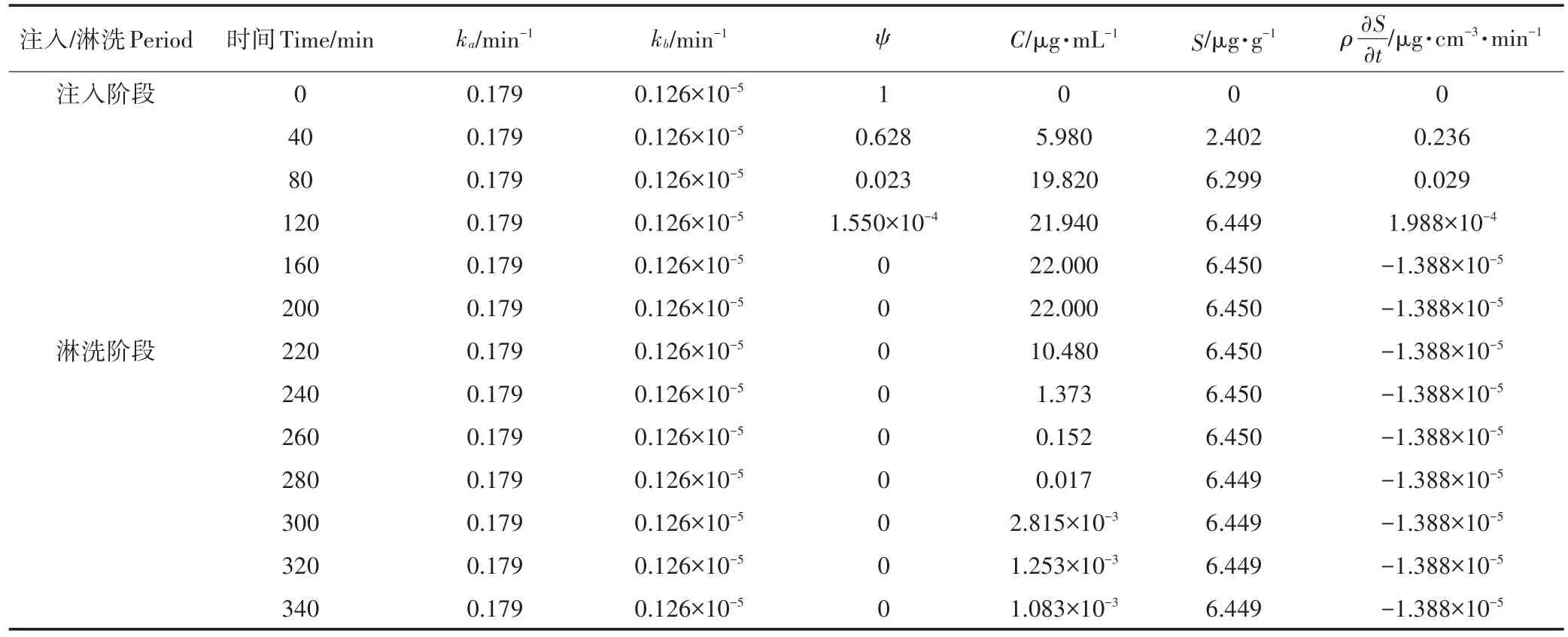
表4 观测孔1吸附-解吸模型源汇项计算值Table 4 Calculation values of source and sink terms of the adsorption-desorption model of the observation hole 1

3 结论

（1）整体调参下，单点非平衡吸附模型在连续注入阿特拉津的条件下，饱和壤质砂土中阿特拉津迁移模拟的NSCs系数为 0.909～0.922，RMSEs为 2.752～3.167，采用单点非平衡吸附模型是适合的；淋洗条件下阿特拉津迁移模拟的NSCs为负值，说明单点非平衡吸附模型不适用于淋洗条件下阿特拉津迁移模拟。

（2）整体调参下，吸附-解吸模型模拟连续注入、淋洗过程中阿特拉津在饱和壤质砂土中的迁移模拟的NSCs为 0.901～0.954，RMSEs为 2.037～3.289，表明吸附-解吸模型模拟连续注入、淋洗过程中阿特拉津迁移均是适合的。

（3）分段调参可提高单点非平衡吸附模型模拟阿特拉津连续注入、淋洗过程中在饱和壤质砂土中迁移的拟合度。