认知无线电中子谱缺失下的似然恢复算法

管 亮,郑 霖,2,张文辉

(1.桂林电子科技大学 a.广西无线宽带通信与信号处理重点实验室; b.广西云计算与大数据协同创新中心,广西 桂林 541004;2.通信网信息传输与分发技术重点实验室,石家庄 050081)

0 概述

近年来,随着无线通信技术的飞速发展,频谱资源短缺的现象日益严重。目前,导致频谱资源匮乏的主要原因是固定频谱分配策略的效率较低[1-2],这一点已被美国联邦通信委员会研究证实。认知无线电能够实现动态频谱接入,从而利用固定分配的频谱资源解决频谱利用效率低的问题[3-5]。

当信道中连续的空闲频段带宽不足以容纳认知用户信号时,频谱分割[6]可以灵活利用信道中的“频谱空穴”,实现认知用户的正常通信。认知用户通过频谱感知技术[7-9]检测空闲频段,利用分割滤波器组进行频域滤波,实现频谱分割,再将分割后的子谱插入空闲频段,从而充分利用空闲琐碎的频带资源。频谱分割是提高频带资源利用率的有效手段,但在实际应用中仍存在许多问题。例如,在时延信道中,由于子谱插空引起相位偏移,因此需要结合相位补偿的方法进行频谱分割。盲相位估计[10]是一种精度较高的方法,其利用未分割前信号相位连续的特性,独立地对相邻子频谱之间的相位偏移进行估计和补偿,不会累计误差。在移动通信中,不同的子频带会产生不同的多普勒频移,因此,在频谱聚合前需要对子频带频率进行精确估计或修正,才能实现原信号的聚合恢复[11]。当用户信号频带宽度大于空余频带的总和,或者“插空”信道出现强干扰时,部分频带将丢失或受严重干扰,导致用户信号波形畸变,影响用户信号检测,因此,在上述场景下,对频谱分割系统的信号恢复进行研究是非常必要的。

本文提出一种自适应信号恢复算法,在频谱分割的基础上构建系统模型,分析在子频带缺失或受干扰时对系统造成的影响。在此基础上求解子谱带缺失情况下的信道离散脉冲响应,并利用最大似然的方式恢复失真信号,从而提升认知无线电中子谱缺失下的信号检测性能。

1 系统模型

1.1 场景模型

图1给出频谱分割下信道中的频段占用情况,其中,当前用户A为认知用户,其信号带宽为wd,通过频谱分割得到3个子谱,分别为wd1、wd2和wd3,授权用户B和授权用户C分别占用信道中的两处连续频带,剩余空闲信道离散地分布在整个信道中。图1(b)表示当前空闲信道带宽不足的情形,其只能容纳用户A的两个子谱wd1和wd2,子谱wd3无法传输。图1(c)表示部分空闲频带出现强干扰的情形,用户A的子谱wd3受到强干扰,使得传输数据受到影响。

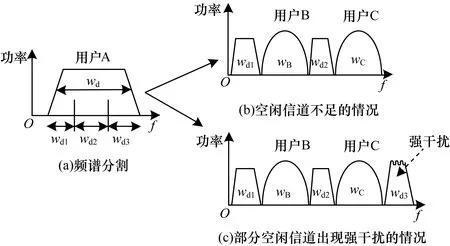
图1 信道中的频段占用情况

假设用户A的发射信号和信道冲击响应分别为x(t)和h(t),则接收信号y(t)可以写作如下形式:

y(t)=x(t)×h(t)+n(t)

(1)

其中,n(t)代表均值为0、方差为δ2的高斯白噪声,结合文献[5]的分割聚合滤波器公式可知,在理想高斯信道下,h(t)对应的频域形式如式(2)所示。

(2)

其中,n为分割子带数,βk为成型滤波器的滚降系数,Bk为分割子带k的带宽,fck为第k个子带的中心频率,H(βi,f,B)的表达式如式(3)所示。

(3)

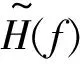
(4)

接收信号可以写作如下形式:

(5)

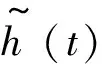
1.2 模型分析

图2给出频谱分割系统和无码间串扰系统的频幅特性示意图。如图2(a)所示,由于频谱分割算法中βkBk=βk+1Bk+1=βoB,因此各子谱的过渡带等宽,在合并重叠的左、右过渡带时,必然拥有相等的增益,保证过渡带合成的信号能够完美恢复原信号。证明过程如下:

(6)

其中,X(w)是原信号谱,加号前后的2项分别表示子带k的右过渡带和子带k+1的左过渡带,fck和fck+1分别为第k个和第k+1个子带的中心频率。

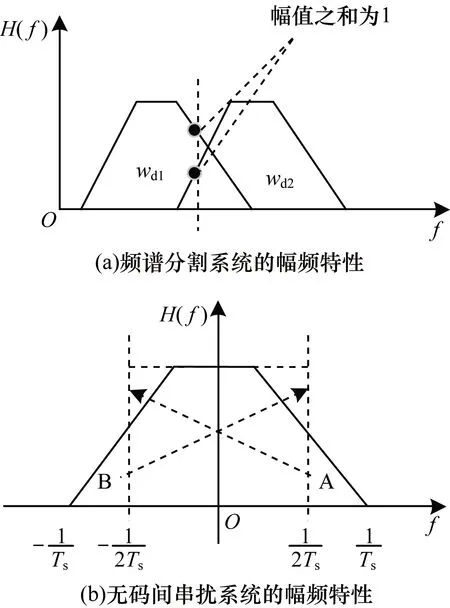
图2 频谱分割系统与无码间串扰系统幅频特性示意图

根据奈奎斯特第一准则[12],系统无码间串扰必须满足如下公式:

(7)

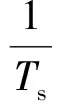
2 似然信号恢复算法

2.1 子谱缺失下信道的冲激响应

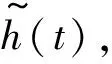
(8)

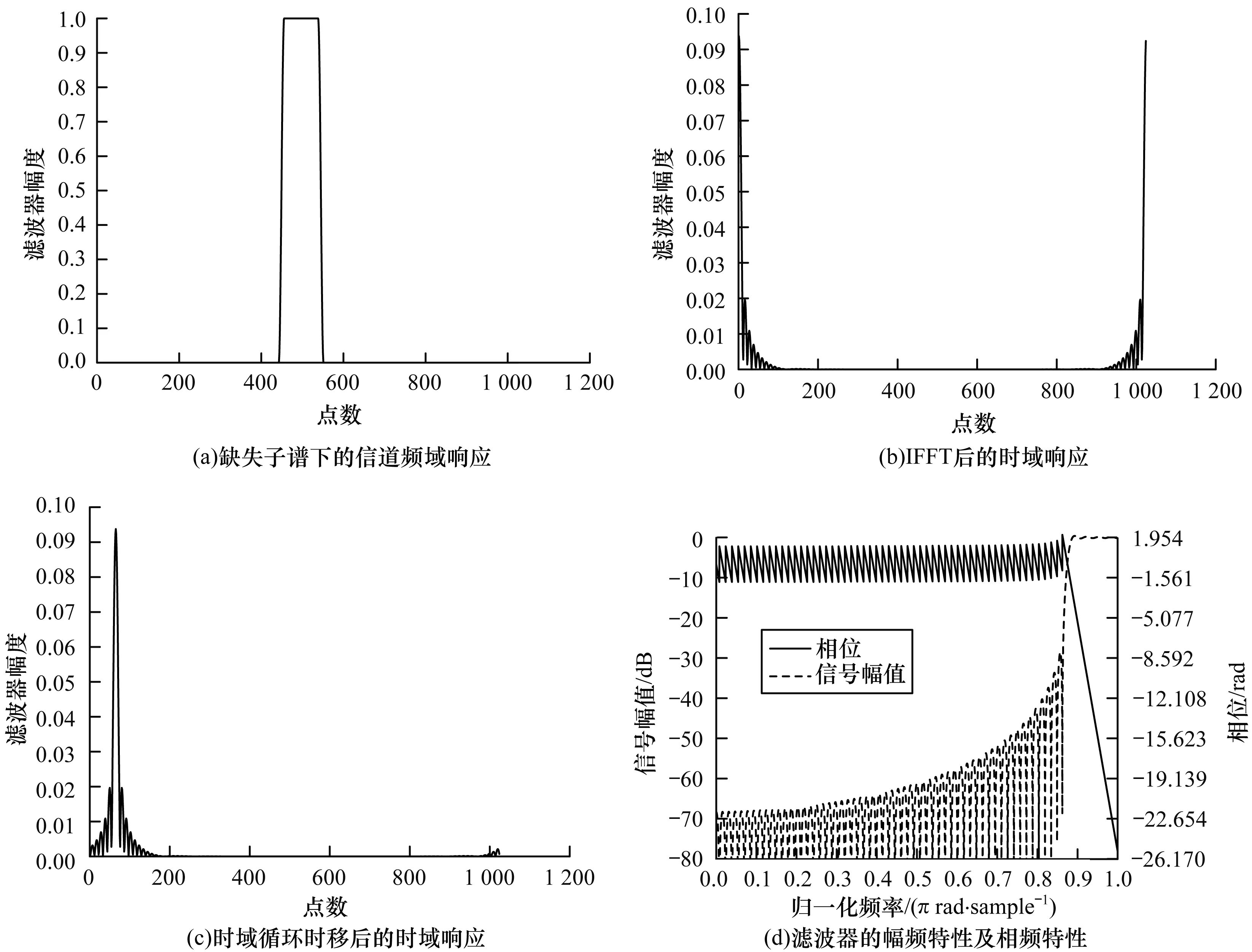
图3 缺失子谱下的信道时域、频域响应及其相频特性

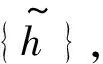
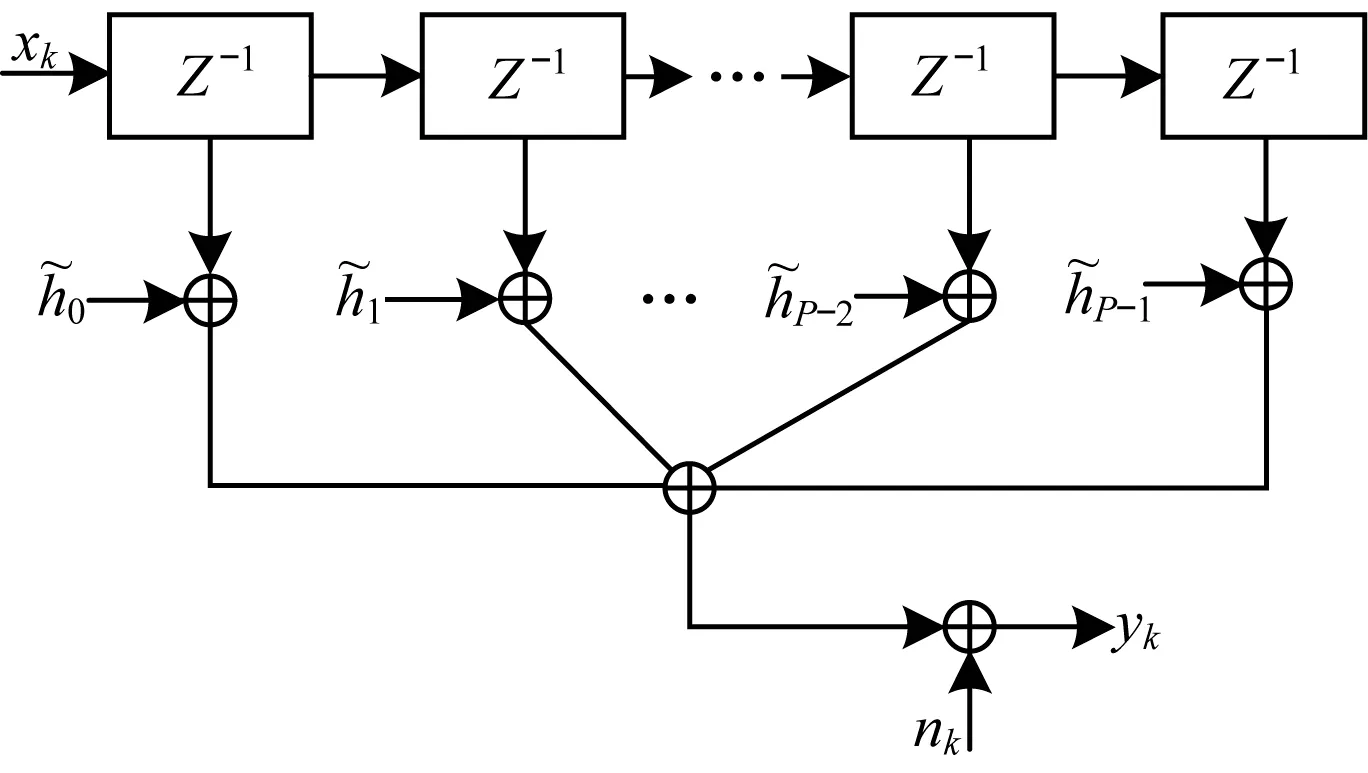
图4 信道FIR模型

通过抽样判决器对y(t)进行抽样判决,则接收信号为:

(9)

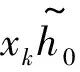
2.2 似然信号恢复

数据信息在通过上述信道后,根据最大似然的序列准则[13-15],需要求出整个数据序列{x}的似然函数。由式(9)可知,在给定数据序列的情况下,yk的条件概率如式(10)所示:

f(yk|{x})=f(yk|xk,xk-1,…,xk-P+1)=

(10)

假设{x}已知,yk间彼此相互独立,对于给定{y}有如下公式:

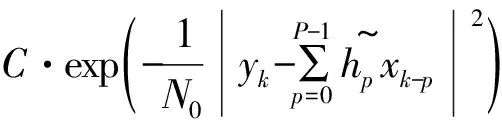
(11)

式(11)等价于{x}的最小价值函数,如式(12)所示。

(12)

当f({y}|{x})取得最大值,即V({x})的值最小时,得到的数据序列即为最佳发送数据序列{x}ml,如式(13)所示。

{x}ml=argmaxf({y}|{x})=argminV({x})

(13)

根据yk的表达式,可忽略噪声影响,得到式(14)。

(14)

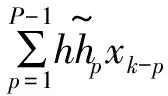
k=0,1,…,L-1

(15)

(16)

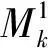
图5 P=2时的分支度量栅格图

3 仿真结果与分析

为了验证自适应似然信号恢复方法的性能,本节给出仿真分析,具体参数如表1所示。

表1 子谱再生系统仿真参数

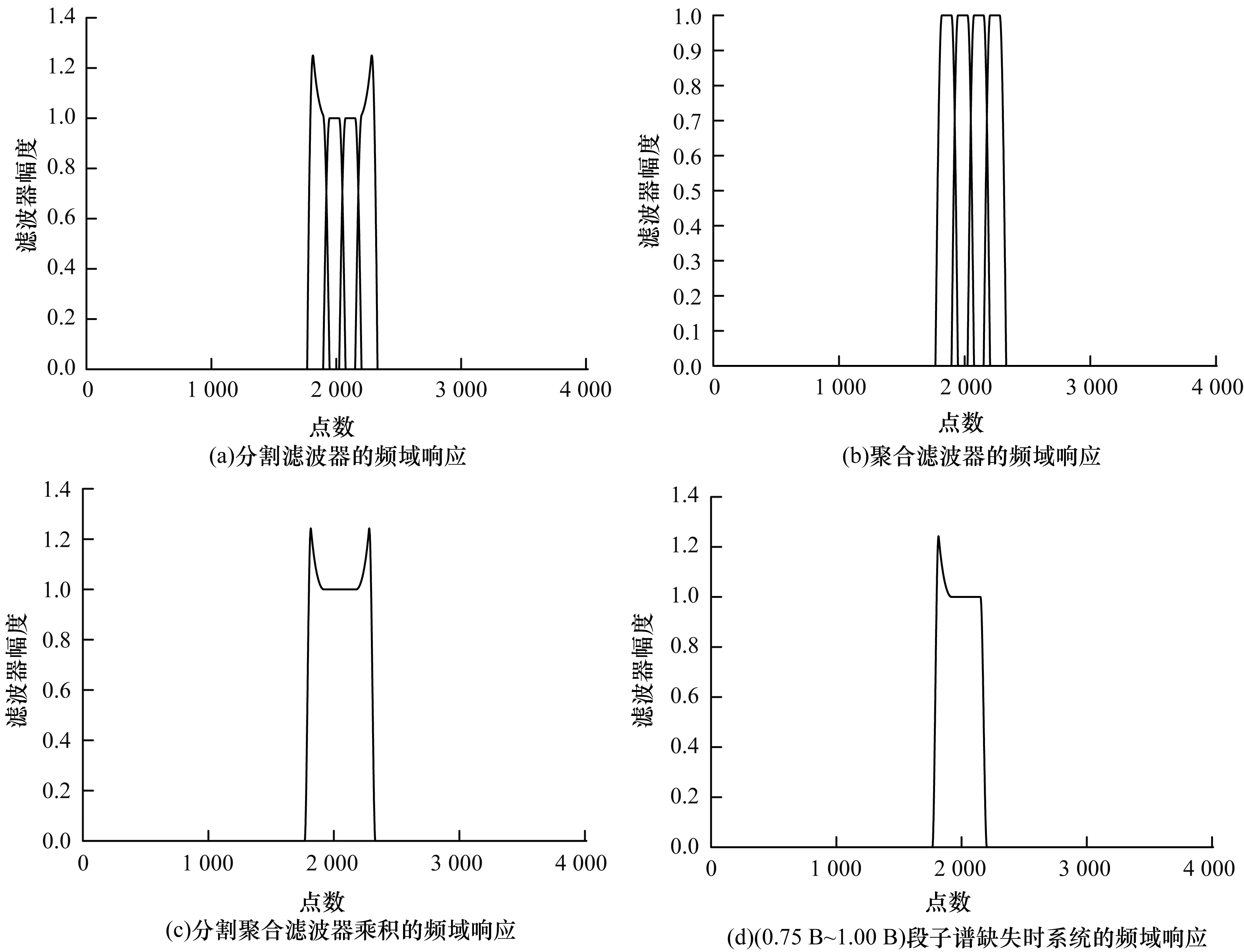
图6 分割滤波器与聚合滤波器的频域响应

图7给出子谱缺失率α为0、1/8、1/4和3/8时,系统采用似然信号恢复方式与不采取任何信号恢复措施(图中表示为None)时的误码率变化曲线。α取1/8、1/4和3/8分别对应信号缺失频段(0.875 B～1.000 B)、(0.75 B～1.00 B)和(0.625 B～1.000 B)。

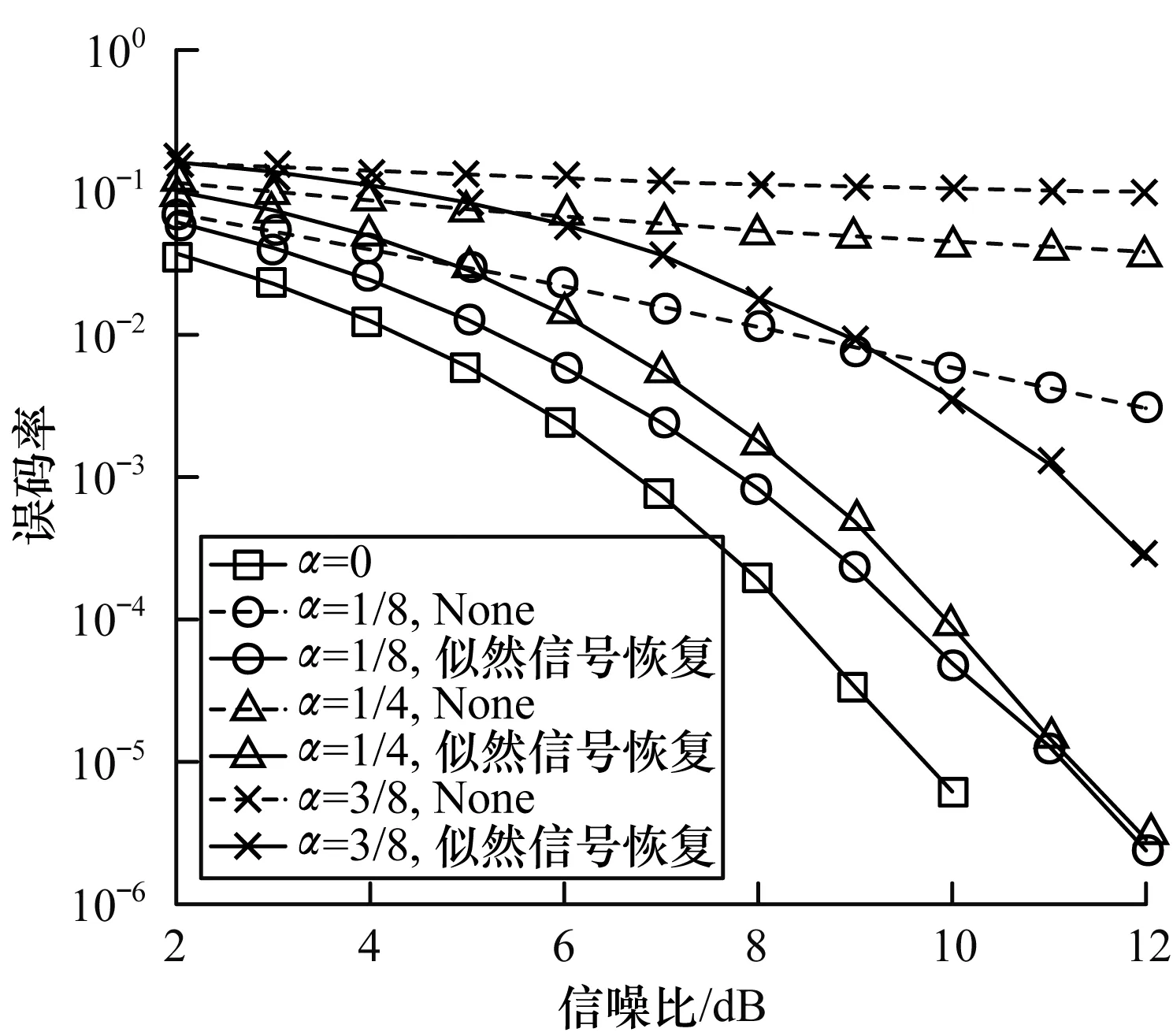
图7 似然信号恢复算法在不同子谱缺失率下的误码率对比

可以看出,在没有采用子谱再生算法时,子谱缺失引起的码间串扰导致信号失真严重,即使在高信噪比条件下,误码率依旧很高,且系统性能随着缺失带宽的增加呈明显的下降趋势。在相同子谱抑制率下,本文方法能够有效抑制因子谱缺失而产生的干扰,提升系统的抗干扰性能,当子谱抑制率α为1/4,信噪比为10 dB时,系统的误码率降至10-4以下。

图8给出子谱缺失率α为1/4时,本文算法与利用前向纠错(Forward Error Correcting,FEC)的子谱再生算法[17-19]的误码率性能曲线,其中,FEC方法选择Turbo码和卷积码2种编码方式。可以看出,在没有采取信号恢复措施时,信号受到严重干扰。采用Turbo码的子谱再生算法在误码性能上优于本文的似然信号恢复算法,同时这两者均优于采用卷积码的子谱再生算法。主要原因在于,基于FEC的子谱再生算法引入了冗余编码,通过牺牲信道效率换取传输可靠性,从而降低了系统的误码率。但由于不同FEC的纠错方式不同,因此性能上会存在差异,且FEC的子谱再生算法使用了多次译码迭代,其算法复杂度较高,并且更易受噪声等干扰的影响。似然信号恢复算法在没有引入编码冗余的条件下充分利用信道特征,其算法复杂度低,即使在强干扰的情况下误码率依然较低。

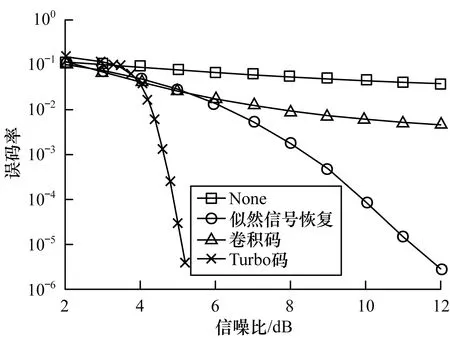
图8 似然信号恢复算法与基于FEC的子谱再生算法误码率对比

4 结束语

本文提出一种似然信号恢复算法。通过分析频谱分割系统的频域响应,构建子谱缺失下的等效信道模型,根据离散脉冲响应,利用最大似然方式减弱频谱缺失造成的干扰。仿真结果表明,该算法能够有效恢复失真信号,与基于FEC的子谱再生算法相比,其子谱缺失下的检测性能较好,不仅避免了编码冗余,还能够保持信息的传输速率,保障频谱分割与聚合系统在复杂环境中的通信性能,同时也为频谱分割与聚合系统提供了一种主动抑制频谱的思路。下一步将选择对整体性能影响最小的子谱进行主动抑制,并在接收端采用似然信号恢复算法规避衰落或干扰频段,以获得更好的解调性能,起到频域均衡的作用。