面向车辆目的地推测的时空搜索优化

韩 磊,於志勇,2,3,朱伟平,於志文

(1.福州大学 数学与计算机科学学院,福州 350116; 2.福建省网络计算与智能信息处理重点实验室,福州 350116;3.空间数据挖掘与信息共享教育部重点实验室,福州 350002; 4.西北工业大学 计算机学院,西安 710072)

0 概述

随着我国城市化进程的不断加快,城市建设取得了巨大成就,但是,城市人口密度大、人员流动性强的状况也引起了一些公共安全问题,车辆目的地推测对解决城市公共安全问题具有重要意义。警察获知目标车辆某时刻从某地出发,其需要尽可能准确地掌握该车辆的目的地以制定行动计划。然而,在很多情况下,由于数据丢失、隐私保护等原因,使得准确推测该车辆的目的地十分困难。此时,警察可以通过已知的目标车辆位置信息来推测其目的地,但是由于已知车辆信息太少(在通常情况下,警察只知道车辆的出发时刻和出发位置),其目的地推测的准确率通常不高。

目前,在城市道路中分布着大量进行全天录像的摄像头,可通过这些视频数据来获取更多关于目标车辆的途经信息,进而提高车辆目的地推测的准确率。从视频中识别目标车辆的途径信息,需要一定的人工和机器成本,且摄像头数量规模庞大,通过所有的视频数据进行全时全域搜索时难度巨大。因此,通过尽可能少的时空搜索(通过搜索城市摄像头视频数据来查看某个时刻目标车辆是否途经某个位置)来准确推测出目标车辆的目的地,引起了研究人员的广泛关注。

本文研究面向目的地推测的时空搜索优化问题,通过对道路摄像头的所有视频录像进行时空搜索以获取车辆的途经信息,从而提高车辆目的地推测的准确率。在此基础上,使用基于概率的单一指标、基于概率和基尼指数的复合指标[1]以及基于概率和信息增益的复合指标[2]来评价时空搜索方法的性能。

1 相关工作

针对目标搜索问题,文献[3]提出并建立了一种海上立体搜寻全局优化模型,文献[4]就飞机发生事故失去动力后黑匣子落水点的位置问题进行了研究,文献[5]以马航事件为背景,基于贝叶斯方法提出一种针对特定区域的失踪目标搜索算法。

基于已知车辆位置信息判断车辆目的地是移动预测的目标,针对该问题,文献[6]提出了一种基于移动性近似的目的地预测算法,该算法关注轨迹本身的运动行为以寻找潜在目的地,然后利用移动梯度下降法来确定目标的目的地。文献[7]研究了个人社会信息和出行信息对出行目的地选择行为的影响。文献[8]通过调查GPS数据,建立利用Markov模型进行目的地预测的概率模型。文献[9]根据人类日常移动路线表现出的时间和空间的规律性,使用拓展的连续路径模式挖掘算法从轨迹中提取运动模式,并从该运动模式中构建模式树以进行目的地预测。此外,在历史信息中(如道路状况、驾驶习惯[10]和轨迹长度[11-13]等)加入外部信息也可以提高预测的准确率。文献[14]提出了SMLP算法,该算法在Markov模型的基础上利用网络内用户的相关性对位置进行预测。

主动感知指智能体采取一定行为以获取更多环境相关信息。在机器视觉[15]和机器人学领域,主动感知已经被广泛应用于定位和导航任务[16]。此外,主动感知还在同步定位和映射[17]、越野驾驶[18]、机器人探索[19]、雷达目标追踪、声呐和光电探测器[20]等方面得到应用。基于车辆起始位置,通过时空搜索获取更多车辆途经信息以提高车辆目的地预测准确率的思想与主动感知[21]相似。在一个主动感知过程中,系统会根据环境状态主动执行感知行为[22]以对环境进行认知。

本文针对城市中的目标车辆搜索问题,提出一种面向目的地推测的时空搜索优化算法,该算法主要包括移动预测和主动感知2个部分。传统目的地预测方法无车辆途经点搜索过程,本文算法增加了这一过程,以获取更多车辆途经信息。

2 问题定义

为了更好地定义面向目的地推测的时空搜索优化问题,本文定义如下符号:令摄像头视频集合D={d1,d2,…,d|D|},位置集合L={l1,l2,…,l|L|},行程集合N={n1,n2,…,n|N|},行程时间序列T=,车辆集合C={c1,c2,…,c|C|},车辆行程轨迹集合TR={tr(cr,nu)},其中,tr(cr,nu)=<(t1,lt1),(t2,lt2),…>|cr,nu。已知车辆cr的出发时间t1和出发位置lt1后,搜索时刻为tk,搜索位置为li,时空搜索结果为q(cr,tk,li),当目标车辆cr在tk时刻出现在位置li时,q(cr,tk,li)=1;否则记为q(cr,tk,li)=0,如式(1)所示。

(1)

IInterval表示搜索时刻与车辆起始出发时刻的差值,即IInterval=tk-t1。最后,本文将q(cr,tk,li)实例化后的tk、li称为time-location,需要考虑(t|T|-t1)×|L|个候选time-location。

在一般情况下,车辆到达目的地后就无法通过城市道路摄像头搜索到该车辆,因此,本文假设车辆当前行程结束后短时间内将无法通过摄像头视频数据再次搜索到该车辆的踪迹。此外,查询视频录像的成本(包括人力和机器成本)远大于模型训练和目的地推测的计算成本,因此,完成车辆目的地推测任务的代价可通过时空搜索次数N来预估,使用AAccuracy作为模型性能的评估度量,AAccuracy表示车辆cr在行程nu中目的地lx的推测准确率,计算公式如下:

(2)

其中,#tr()表示轨迹条数。

问题(面向目的地推测的时空搜索优化)给出车辆的历史行程轨迹集合T′R、车辆cr行程nu的起始时刻t1、起始位置lt1,以及当天可供时空搜索使用的道路摄像头视频录像数据dj。优化目标是在N次时空搜索q(cr,tk,li)的条件下最大化车辆cr行程nu的目的地lx推测的准确率AAccuracy。优化问题表达式如下:

givecr,nu,(t1,lt1),T′R,N,q(cr,ti,lk)indj

returnlx,s.t.maxAAccuracy

(3)

3 车辆目的地推测

假设已知车辆历史行程轨迹T′R,在仅知道车辆某时刻从某地出发的情况下推测该车辆的目的地,方法有以下2种:根据车辆的起始位置信息推测出车辆目的地;通过时空搜索获取车辆途经信息,再结合车辆的起始位置信息推测车辆目的地。

对于第1种方法,本文基于简单一阶Markov模型进行实现,其推测车辆目的地的流程如图1所示。

图1 基于简单一阶Markov模型的车辆目的地推测

设车辆位置转移概率(简称M)表示车辆从一个位置移动到另一个位置的概率,M计算公式如下:

(4)

(5)

对于第2种方法,本文基于引入时空搜索的一阶Markov模型进行实现,其推测车辆目的地的流程如图2所示。

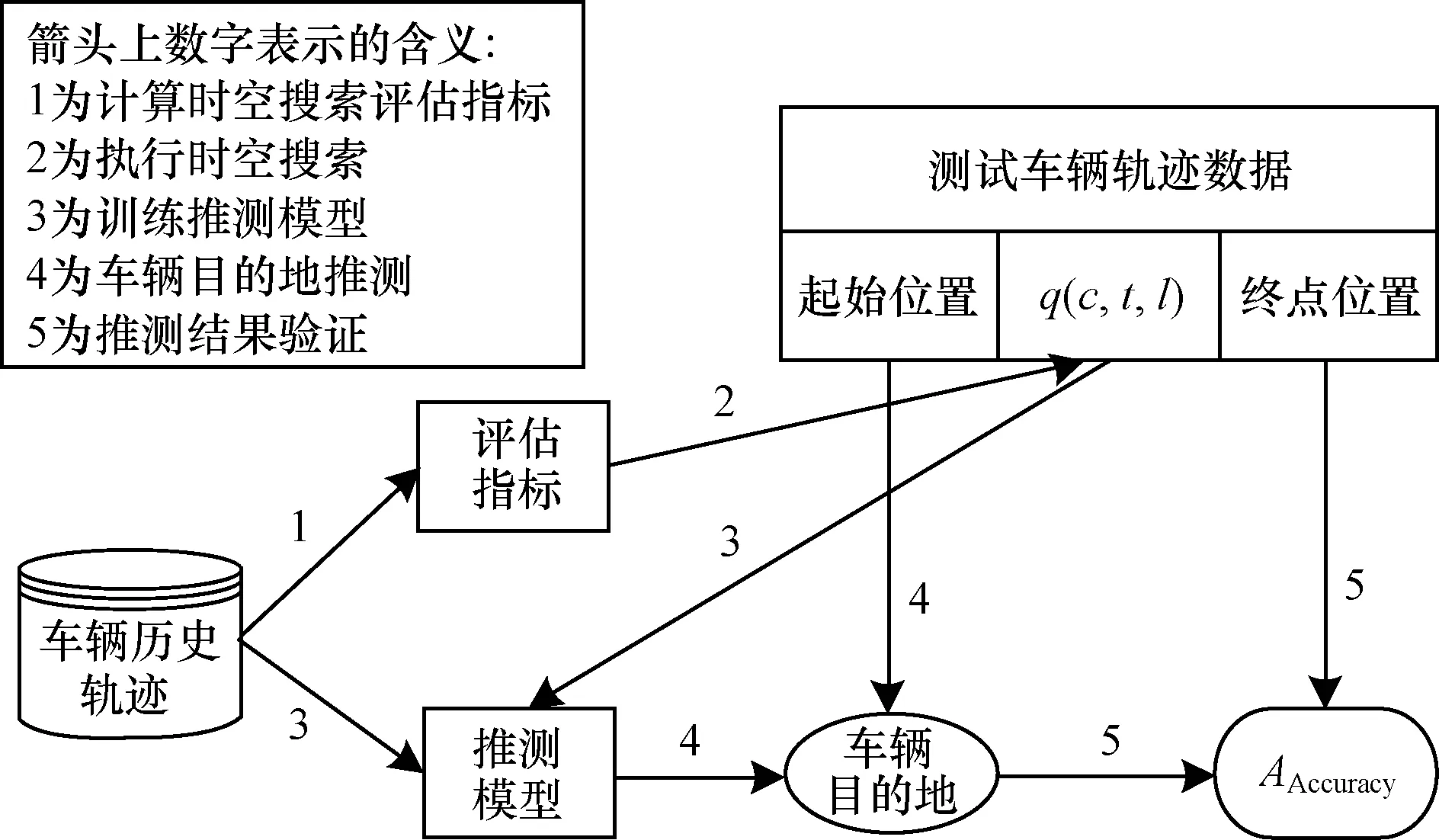
图2 基于改进一阶Markov模型的车辆目的地推测

Fig.2 Vehicle destination inference based on improved first-order Markov model

此时车辆位置转移概率计算如下:

(6)

(7)

由于车辆轨迹信息不足(只知车辆出发位置和出发时刻),基于简单一阶Markov模型推测车辆目的地时的准确率不高,因此本文基于改进一阶Markov模型来推测车辆目的地。在时空搜索方式的选择上,本文提出基于概率的单一指标、基于概率和基尼指数的复合指标以及基于概率和信息增益的复合指标来评估不同时空搜索方式的性能,并基于3种指标分别实现算法CFMM-MidQuery、CFMM-UtilityQuery-Gini和CFMM-UtilityQuery-Info。

3.1 CFMM-MidQuery算法

设车辆cr行程的起始时间为t1,起始位置为li,首先确定车辆cr在tmid时刻的N个可能性最大的位置,表示为lq[1],lq[2],…,lq[j],…,lq[N]。然后执行时空搜索q(cr,tmid,lq[j]),得到N个返回结果,这些结果可能包含一个1(即确定了目标车辆cr在tmid时刻的位置为lq[j])或者所有结果都是0(即tmid时刻在lq[1],lq[2],…,lq[j],…,lq[N]这些位置均未找到目标车辆cr),然后将q(cr,tmid,lq[j])的返回结果作为条件训练一阶Markov模型。该过程为CFMM-MidQuery算法过程,其伪代码如下。

算法1CFMM-MidQuery算法

输入T′R(车辆历史行程轨迹),(cr的起始时刻和位置),tmid(搜索时刻),N(时空搜索次数)

输出车辆cr的终点位置

1.根据T′R计算t1时刻位置为lt1的车辆在tmid时刻的位置分布概率LSm

2.遍历向量LSm,返回N个概率最大的位置编号索引:lq[1],lq[2],…,lq[j],…,lq[N]

3.执行时空搜索q(cr,tmid,lq[j])

4.根据T′R、和时空搜索结果计算终点位置分布概率LSc

5.根据LSc返回概率最大的位置

6.END

3.2 CFMM-UtilityQuery算法

CFMM-MidQuery算法需要先指定搜索时刻,其不能说明哪个搜索时刻是最佳选择,而在CFMM-UtilityQuery算法中,按照效益值大小将不同的候选time-location进行排序,选择效益大的time-location执行时空搜索,然后将返回结果作为条件训练模型(模型构建过程与CFMM-MidQuery相同)。在此基础上,本文分别实现基于概率和基尼指数复合评估指标的CFMM-UtilityQuery-Gini算法与基于概率和信息增益复合评估指标的CFMM-UtilityQuery-Info算法。

3.2.1 CFMM-UtilityQuery-Gini算法

假设目标车辆cr的起始时间为t1,起始位置为lt1。首先,基于概率和基尼指数复合评估指标计算tk时刻搜索位置ls对于推测车辆cr目的地的效用,计算公式如式(8)所示。

(1-ggini(tk,ls))

(8)

式(8)由两部分组成:p(lt1,ls)|(t1→tk)表示q(cr,tk,ls)=1的概率,(1-ggini(tk,ls))用于评估以q(cr,tk,ls)=1作为条件筛选训练数据后车辆cr终点位置分布的混乱程度。若终点位置分布概率为P={p1,p2,…,pk,…,pM},则原始基尼指数计算公式如式(9)所示。

(9)

因此,本文基尼指数计算公式如式(10)所示。

ggini(tk,ls)=ggini{p(lt1,lx)|(t1→t|T|),

q(cr,tk,ls)=1}

(10)

CFMM-UtilityQuery-Gini算法伪代码如下:

算法2CFMM-UtilityQuery-Gini算法

输入T′R(车辆历史行程轨迹),(车辆cr的起始时刻和位置),N(时空搜索次数)

输出车辆cr的终点位置

1.FOR tmid←t1TO t|T|

2.根据T′R计算t1时位置为lt1的车辆在tmid时刻的位置分布概率LSm

3.FOR lmid←l1TO l|L|

4.根据T′R计算t1时刻位置为lt1、tmid时刻位置为lmid的车辆终点位置分布概率LSme

5.END FOR

7.END FOR

,,…,,…,

9.执行时空搜索q(cr,ti,lq[i])并且返回搜索结果

10.根据T′R、和时空搜索结果计算终点位置分布概率LSe

11.返回LSe中概率最大的位置

12.END

3.2.2 CFMM-UtilityQuery-Info算法

假设目标车辆cr的起始时间为t1,起始位置为lt1。首先,基于概率和信息增益复合评估指标计算tk时刻搜索位置ls对于推测车辆cr目的地的效用,其计算公式如式(11)所示。

(11)

其中,Iinfo(tk,ls)评估q(cr,tk,ls)=1作为条件筛选训练数据后车辆终点位置分布的混乱程度。若终点位置分布概率为P={p1,p2,…,pk,…,pM},则熵计算公式如式(12)所示。

(12)

因此,本文信息增益计算公式如式(13)所示。

Iinfo(tk,ls)=E{p(lt1,lt|T|)|(t1→t|T|)}-

E{p(lt1,lt|T|)|(t1→t|T|),

q(cr,tk,ls)=1}

(13)

CFMM-UtilityQuery-Info算法伪代码如下:

算法3CFMM-UtilityQuery-Info算法

输入TR′(车辆历史行程轨迹),(车辆cr的起始时刻和位置),N(时空搜索次数)

输出车辆cr的终点位置

1.根据T′R计算t1时刻位置为lt1的车辆终点位置分布概率LSse

2.根据LSse和式(12)计算熵E1

3.FOR tmid←t1TO t|T|

4.根据T′R计算t1时位置为lt1的车辆在tmid时刻的位置分布概率LSm

5.FOR lmid←l1TO l|L|

6.根据T′R计算t1时刻位置为lt1、tmid时刻位置为lmid的车辆终点位置分布概率LSme

7.根据LSme和式(12)计算熵E2

8.END FOR

10.END FOR

12.执行时空搜索q(cr,ti,lq[i])

13.根据T′R、和时空搜索结果计算终点位置分布概率LSe

14.返回LSe中概率最大的位置

15.END

4 实验结果与分析

4.1 原始数据描述

本文的实验数据来自滴滴出行平台(https://gaia.didichuxing.com),原始数据为成都市部分区域的滴滴订单数据,采集区域的面积大小约为8.37 km×8.35 km,采集日期范围为2016年11月1日—2016年11月30日,原始数据信息如表1所示。

表1 原始数据信息

4.2 实验数据预处理

在数据集中,不同车辆的GPS点是无序的,需要对数据集中车辆订单ID和时间使用二级排序算法生成出租车的GPS点序列。由于原始数据时间精度为3 s,如果同一行程轨迹相邻两GPS点的时间相差超过3 s,则认为该轨迹数据部分缺失,按照3 s的时间精度补全缺失数据。如果缺失时长不超过60 s,则在该段缺失时间内车辆被认为是匀速直线行驶;若缺失时间超过60 s,则认为该轨迹缺失严重,将其舍弃。

在排好序的出租车GPS点序列中,每辆车每分钟包括若干个GPS坐标点,且不同分钟内GPS点的个数不同,因此,本文以分钟为单位将时间离散化,每分钟仅取时间最小的一条位置数据表示车辆在该时间的位置。最后根据数据范围将该区域划分成大小约为0.93 km×0.93 km的方格[23](共计81个网格),将车辆的轨迹数据投影到网格中,一个网格就代表一个位置区域。

4.3 结果分析

本文基于相同的实验数据集,测试不同阶Markov模型推测车辆目的地的准确率,结果如图3所示。从图3可以看出,当Markov模型阶数达到3时,车辆目的地推测的准确率达到最高(2阶Markov模型和3阶Markov模型在推测车辆目的地时的准确率基本一致),然后随着模型阶数的增加其推测准确率逐渐降低,因此,当有多个时空搜索返回结果为1时,本文仅选择一个time-location参与模型的训练与预测。

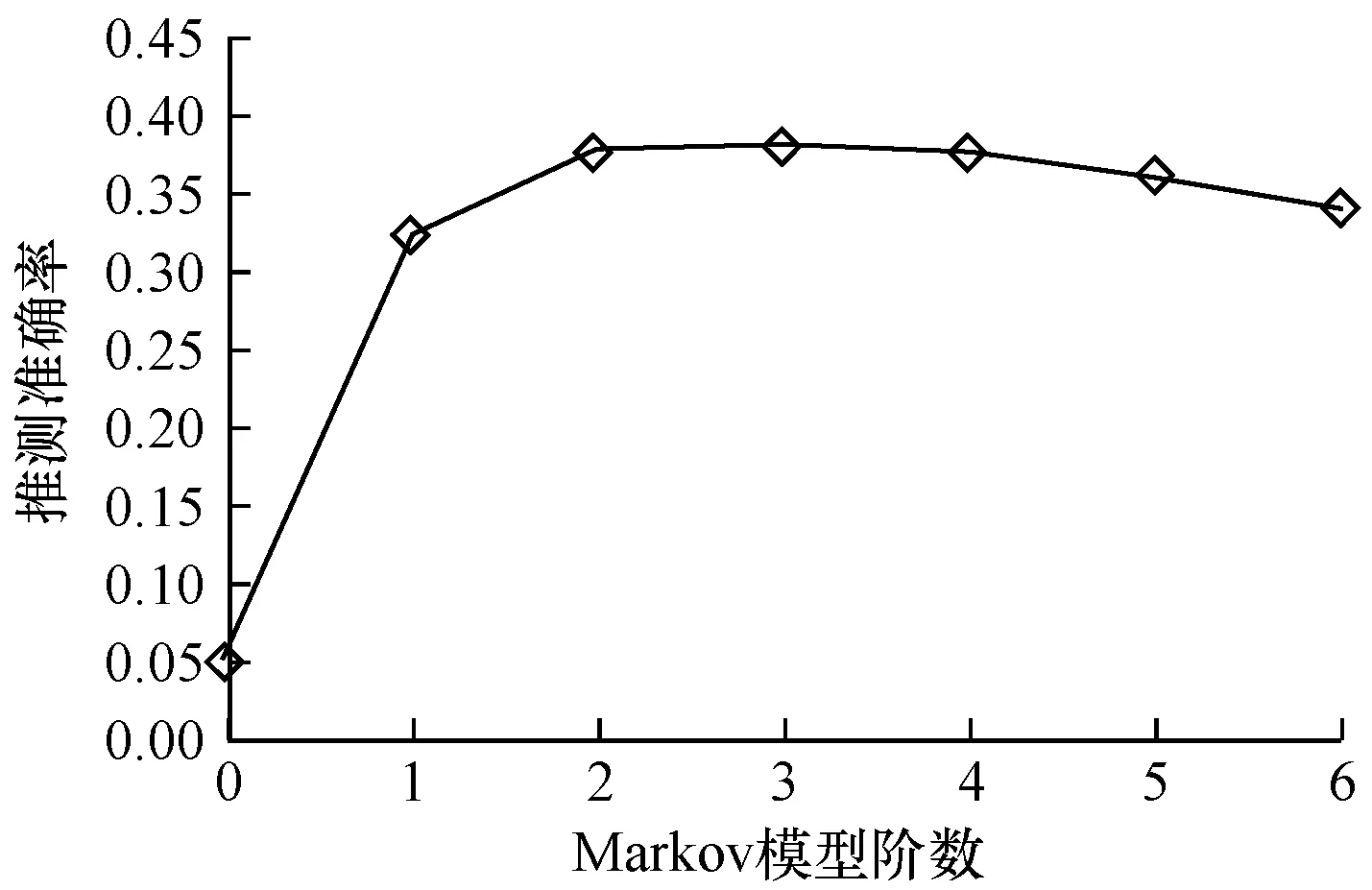
图3 不同阶数Markov模型的推测性能对比

Fig.3 Comparison of inference performance of Markov models with different orders

为研究相同数据集下车辆目的地推测准确率与IInterval的关系,本文基于二阶Markov模型改变IInterval(固定起始时间,改变中间搜索时刻),测试模型推测准确率,结果如图4所示。从图4可以看出,随着IInterval的增大,车辆目的地推测的准确率也逐渐提高。因此,当有多个时空搜索返回结果为1时,本文仅选择IInterval最大的time-location参与模型的训练与预测。

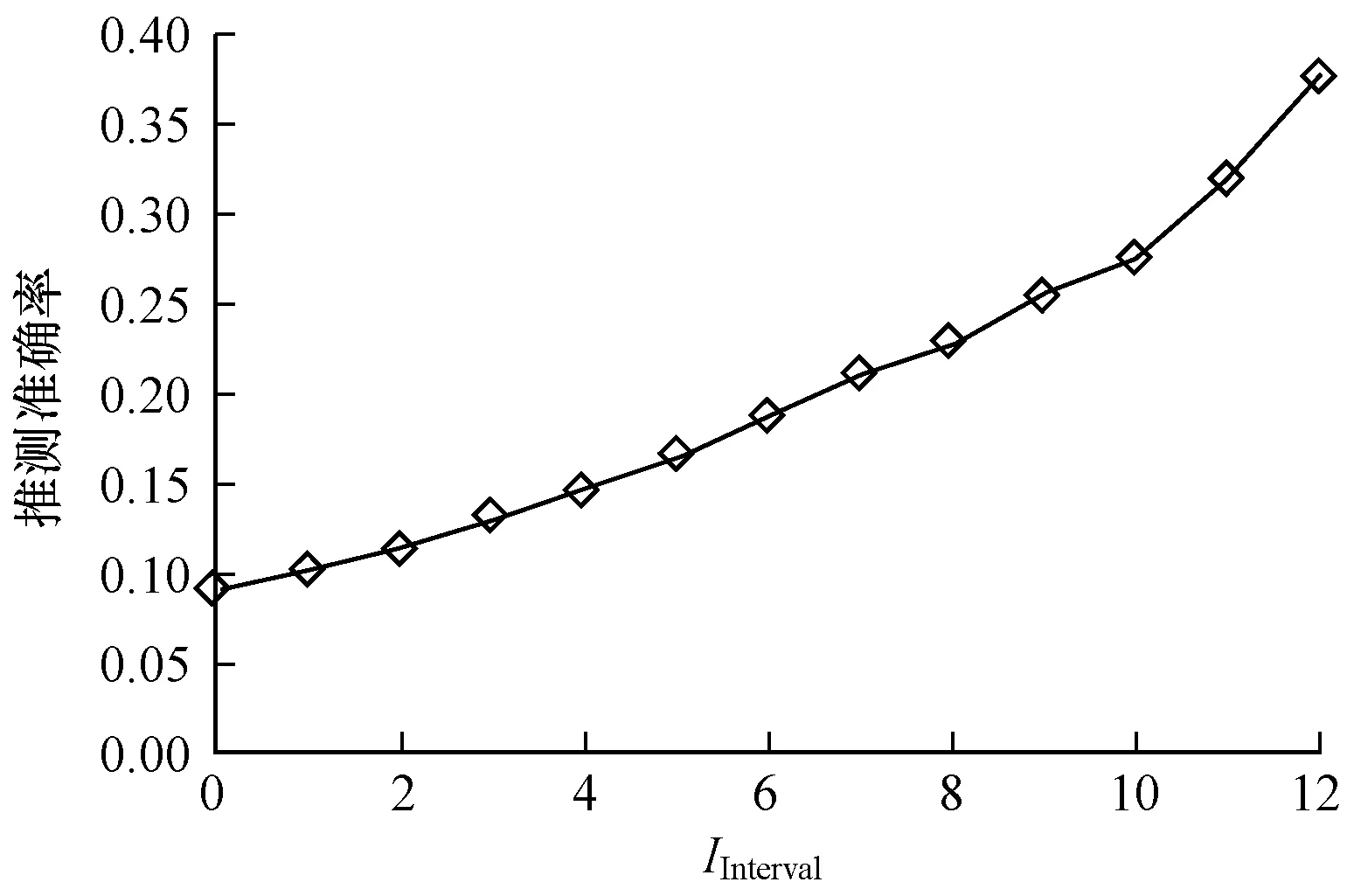
图4 不同IInterval时的二阶Markov模型推测准确率

Fig.4 Inference accuracy of second-order Markov model with differentIInterval

图5所示为不同行程时长下的轨迹统计情况,由图5可以看出,随着时长的增加,大于该时长的轨迹比例逐渐减小,即在搜索时刻逐渐增大时,通过摄像头视频录像找到车辆的可能性将降低。

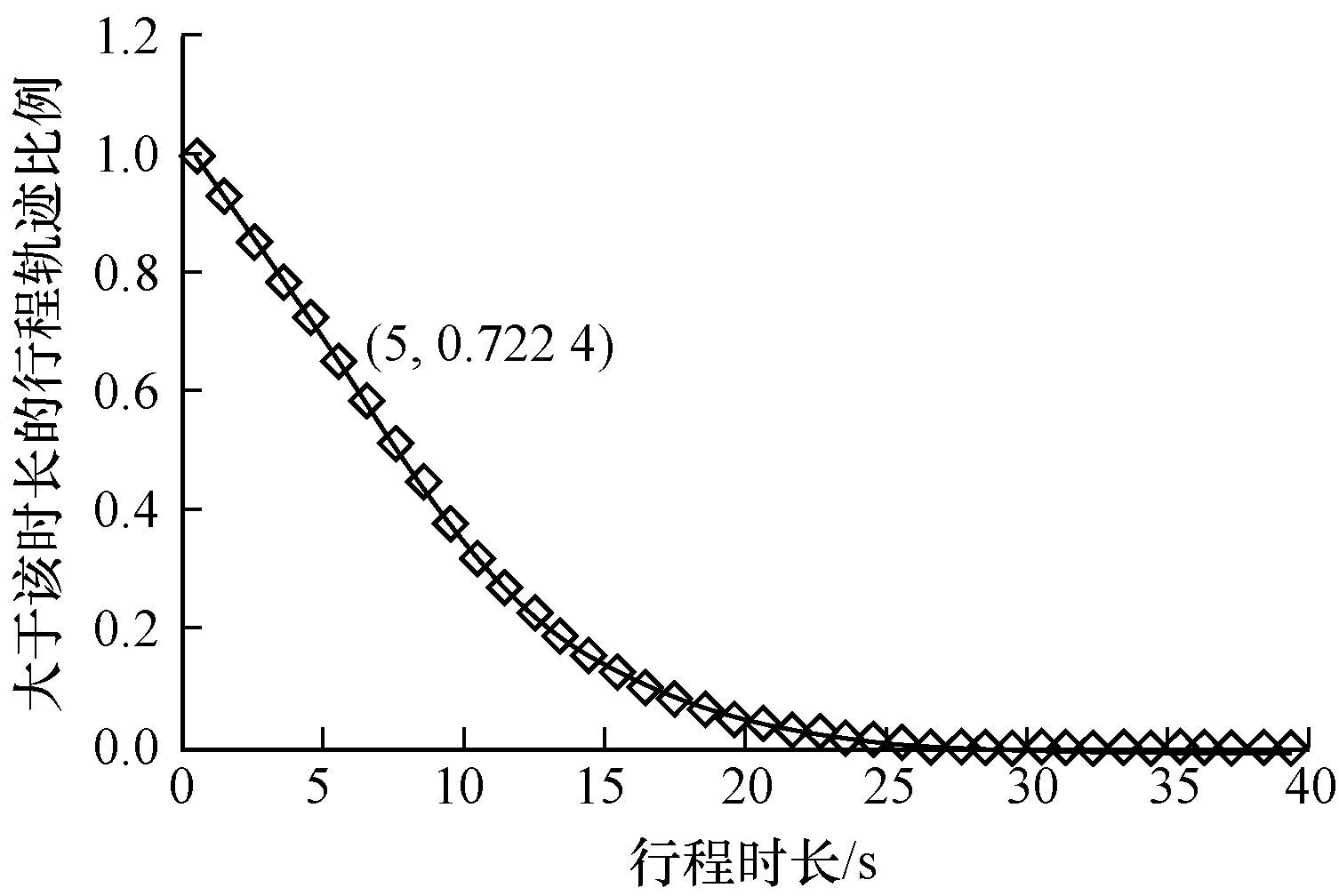
图5 不同行程时长下的轨迹统计情况

由图4可以看出,随着IInterval的增大,车辆目的地推测的准确率逐渐提高;由图5可以看出,随着搜索时刻的增大,行程时长大于该搜索时刻的轨迹比例逐渐减小。因此,CFMM-MidQuery算法很难选择合适的中间搜索时刻。本文基于二阶Markov模型,测试相同搜索次数下不同中间搜索时刻时车辆目的地推测的准确率,结果如图6所示,从图6可以看出,在相同搜索次数下,IInterval为5 min时,CFMM-MidQuery算法推测车辆目的地的准确率最高。

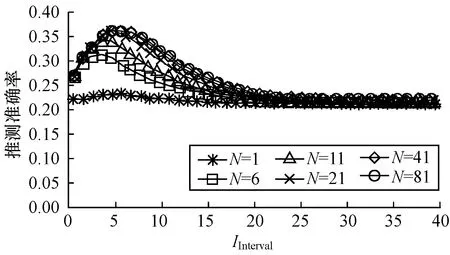
图6 不同搜索时刻下CFMM-MidQuery算法推测准确率

Fig.6 Inference accuracy of CFMM-MidQuery algorithm at different search times

由图6可以看出,当搜索时刻为5 min时,CFMM-MidQuery算法的性能较好,因此,将CFMM-MidQuery算法的搜索时间定为5 min,本文将之称为CFMM-MidQuery-5算法。比较CFMM-MidQuery-5、CFMM-UtilityQuery-Info、CFMM-UtilityQuery-Gini 3种算法,结果如图7所示。从图7可以看出,当N较小时,CFMM-UtilityQuery-Gini和CFMM-MidQuery-5算法推测车辆目的地的准确率没有太大区别,且2种算法略优于CFMM-UtilityQuery-Info算法;当N进一步增大时,CFMM-UtilityQuery算法推测车辆目的地的准确率明显高于CFMM-MidQuery-5算法,而CFMM-UtilityQuery-Info、CFMM-UtilityQuery-Gini 2种算法在推测车辆目的地的准确率方面无明显区别。基于概率单一指标的方法只考虑当前时空搜索找到目标车辆的概率,不考虑当前时空搜索对车辆目的地推测的效用,并且该指标需要指定搜索时刻,限制了时空搜索范围,导致时空搜索次数较高时无法执行更合适的时空搜索;信息增益和基尼指数都是评价车辆位置分布混乱程度的度量,都能在客观上反映车辆位置的概率分布情况,因此,这2种复合指标在推测车辆目的地的准确率方面无明显区别。

图7 不同搜索次数下3种算法车辆目的地推测准确率对比

Fig.7 Comparison of inference accuracy of vehicle destination using 3 algorithms under different search times

5 结束语

获取目标车辆更多的行程途经信息可以提高车辆目的地推测的准确率。本文提出基于概率和基尼指数的复合指标与基于概率和信息增益的复合指标,不仅考虑当前时空搜索下找到目标车辆的可能性,还兼顾当前时空搜索对目的地推测的长期效用。复合指标无需指定搜索时间,可以将不同时间下的空间搜索进行比较,解决了概率单一指标需要指定搜索时间的问题。实验结果表明,在高搜索次数条件下,复合指标的评估效果明显优于概率单一指标。

本文假设车辆行程结束后短时间内无法通过视频数据再次搜索到该车辆的踪迹,该假设过于理想,下一步将基于车辆一天中的完整轨迹在给定时刻进行车辆位置搜索,以解决上述假设的局限性问题。