Parity-time对称性对电注入半导体激光器的模式控制*

王学友 王宇飞 郑婉华

1) (中国科学院半导体研究所,中国科学院固态光电信息技术重点实验室,北京 100083)

2) (中国科学院大学材料科学与光电技术学院,北京 100049)

3) (中国科学院大学未来技术学院,北京 101408)

4) (中国科学院半导体研究所,集成光电子学国家重点实验室,北京 100083)

非厄米的描述对于开放系统有重要意义,满足parity-time对称性的哈密顿量,其参数在一定范围内可以使能量具有实的本征值.本文通过模拟,研究了损耗大小以及结构对称性对条形波导中的parity-time对称性的影响,并通过实验发现了电注入条件下由parity-time对称破缺导致的脊条波导模式间隔加倍、模式数减半的现象.

1 引 言

能量守恒对于一个闭合系统是很自然的要求,这就会导致系统所对应的本征能量为实数,这时所对应的算符就为厄米算符,描述这个系统的哈密顿量的厄米性可以确保系统能量为实数,相应的数学表达可写为非厄米的哈密顿量会产生复的本征值,这意味着系统不再幺正,这是非厄米哈密顿量无法被人们接受的原因.但很多时候,人们关注的只是闭合系统中一个有限的子空间.为了唯象地描述这种开放系统,开始有科学家们引入非厄米的描述方式.1928 年,Gamow[1]使用复的能量本征值来描述粒子隧穿逃离原子核时的速度,通过量子力学的隧道效应解释了α放射性衰变的随机性.1943 年,Dirac[2]提出通过使用非厄米算符和自洽內积理论来解决场论中的发散问题.1954年,Feshbach等[3]通过引入非厄米的势来描述中子和原子核的散射相互作用.此外还有许多通过非厄米理论来讨论实际问题的工作[4−9].

早期的非厄米系统中,哈密顿量的虚部通常被用来描述系统的耗散,这只是对物理现象的一种非本质的唯象描述,因为这样的描述并不具备幺正性.1998年,基于前人关于非厄米哈密顿量的研究,Bender和Boettcher[10]提出一类满足PT对称性的非厄米哈密顿量,PT对称性中的P是parity,指的是空间反演变换;T是time,指的是时间反演变换,并证明在一定参数的取值范围里,这类哈密顿量的本征能量为实数,哈密顿量形式为H=p2+x2(ix)ε(ε≥ 0),空间反演变换P的作用是:p → –p,x → –x;时间反演变换 T 的作用是:p → –p,i → –i.由此可以看出,空间反演算符P是线性算符,而时间反演算符T是反线性的.对于哈密顿量H,若其与PT算符满足对易关系则称这个哈密顿量具有PT对称性,满足PT对称性的哈密顿量可以表达为当哈密顿量对应的本征函数ψ也满足PT对称性时,通过简单的推导可以发现,这种情况下,能量E 的虚部为 0,满足 E=E*,这样的系统具有严格的PT对称性.同理,当哈密顿量对应的本征函数不满足PT对称性时,通过简单的推导可以证明,如果哈密顿量有本征能量E对应本征函数ψ,那么存在另一个本征函数ψ′,其能量本征值为E*,这意味着系统中的某能量会和它的复共轭同时成对地出现在能谱中.此时,哈密顿量依然满足PT对称性,但系统中仍可能出现复的本征能量,这种情况称为PT对称性的自发破缺.

2 实验设计和模拟分析

首先采用金属有机化学气相沉积法(metal organic chemical vapor deposition,MOCVD)生长了外延晶片,其中波导层由Al(x)GaAs材料构成,其折射率n≈3.42,量子阱由GaAs和GaIn(x)As材料构成,外延片的详细条件在我们之前的工作中有相应报道[23],结构如图1所示.

图1 外延片结构图Fig.1.Epitaxy structure of wafers.

通过标准的光刻工艺制备条形激光器,为了满足PT对称条件,使其中一部分能够通过电注入对激光器提供增益,作为增益区;另一部分为了避免载流子扩散带来的影响,将这部分区域的高掺层通过电感耦合等离子体(inductively coupled plasma,ICP)工艺刻蚀掉,然后由SiO2覆盖,起到绝缘层的效果,由于本征吸收的存在,这部分吸收区可以作为损耗区,结构如图2所示.

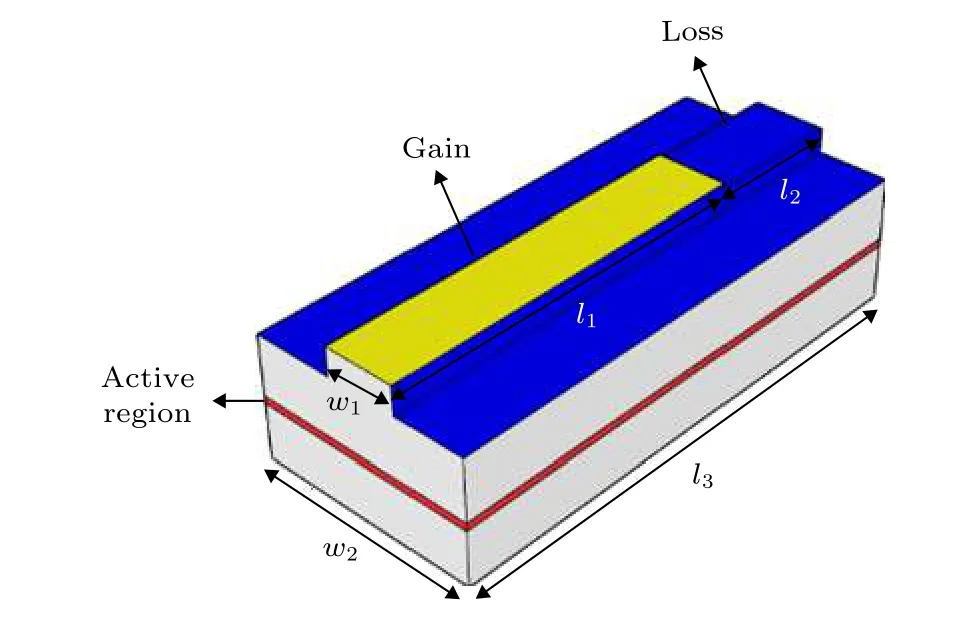
图2 器件结构图,其中黄色部分为增益区,蓝色部分为损耗区Fig.2.Device structure diagram,the yellow part is the gain region and the blue part is the loss region.

其中脊条总长l3=550 μm 的条形波导,增益区长度l1=450 μm,损耗区长度l2=100 μm,条宽w1=7 μm,衬底总宽度w2=300 μm,红色区域为激光器有源区,脊条上黄色区域为增益区覆盖电极,脊条上蓝色部分为损耗区.

激光器测试时由夹具固定不动,通过控制注入电流来对增益区的增益进行调节,将产生的激光通过光纤导入光谱仪中,记录不同电注入水平下,激光器的光谱特性,从而分析电注入条件下PT对称对模式调控带来的影响.

首先计算了条形波导有源腔和无源腔中共振模式的本征频率,波导结构如图3所示.其中黄色部分为增益区,蓝色部分为损耗区,模拟区域的外围通过完美匹配层对泄漏光进行吸收.通过对共振频率的本征值求解,得到复数形式的特征频率f=fR+ifI,其中 fR为特征频率的实部,fI为特征频率的虚部.波导的折射率 n=nR+inI,其中nR为折射率实部,nI为折射率虚部.可以通过对复折射率的设置,来构建一个满足PT对称性的势,即要求 n (x)=n*(-x).分别设置增益区折射率为nl=nRl+inIl,损耗区折射率分布为 nr=nRr+inIr.由于在制备器件后,损耗往往较为固定,可以通过增益的调节来分析PT对称的性质.因此,设另两部分的折射率实部满足 nRl=nRr=3.42,分别固定损耗区折射率虚部为 nIr=-0.01 以及 nIr=-0.05,调节 nIl的大小,计算模式的变化,结果如图4、图5所示.

图3 条型波导模拟结构图Fig.3.Simulation structure of stripe waveguide.

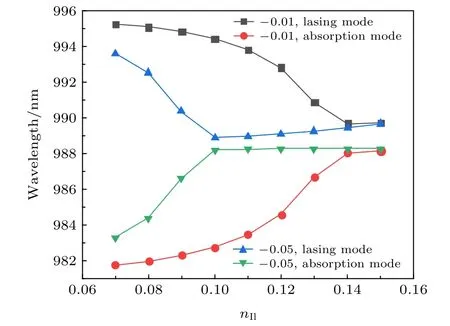
图4 折射率虚部为 n Ir=-0.01和n Ir=-0.05 时,波长与 n Il 的关系图Fig.4.Relationship between wavelength and nIl when nIr=-0.01 and n Ir=-0.05.

图4和图5为固定损耗区虚部为–0.01和–0.05时的模拟结果,其中图4为 nIl和波长的关系曲线图,图5为 nIl和特征频率虚部的关系曲线图.可以看到,随着 nIl的增大特征频率的虚部数值首先增大,达到破缺点后分叉,其中一个模式的虚部迅速减小,演化为吸收模式 (absorption mode),另一个模式的虚部增大,作为发射模式(lasing mode).发射模式和吸收模式被主要限制在增益区和损耗区[18].图中,黑线和红线是固定虚部为–0.01时发射模式以及吸收模式曲线,蓝线和绿线是固定虚部为–0.05时发射模式以及吸收曲线.根据图4可以看出,随着损耗区损耗的增加,PT对称破缺发生时所对应的的 nIl的数值更小,且破缺点的模式简并度更高.根据图5还可以看出,特征频率的虚部在破缺点时的数值还会明显下降.

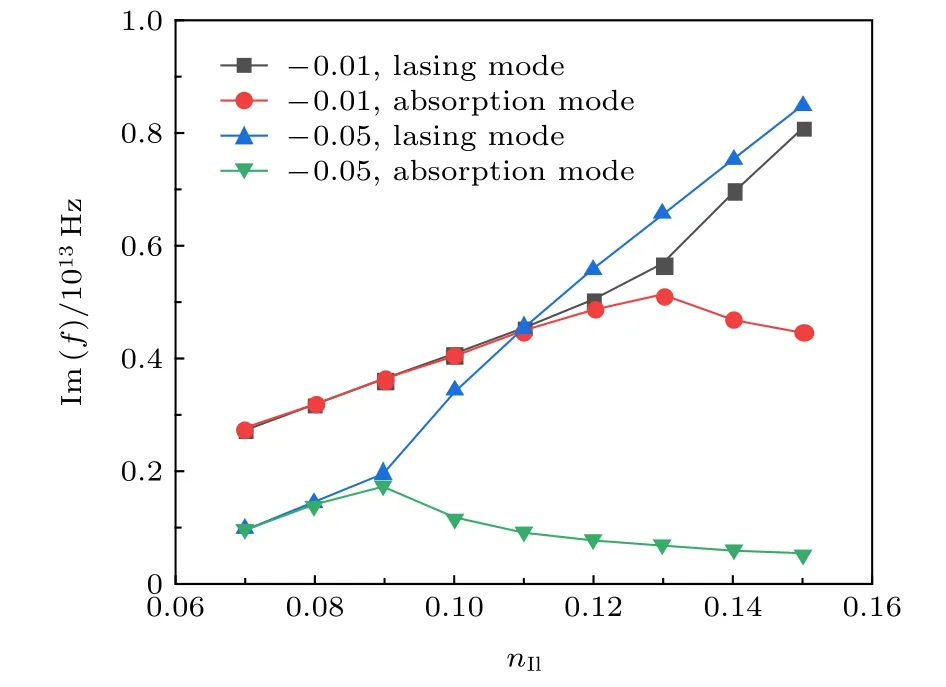
图5 折射率虚部为 nIr=–0.01 以及 nIr=–0.05 时,特征频率虚部与 n Il 的关系图Fig.5.Relationship between the imaginary part of the characteristic frequency and nIl when n Ir=-0.01 and nIr=-0.05.

这个现象可以通过耦合模方程来理解[24]:

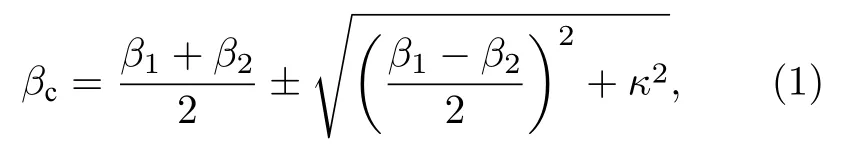
其中βc为耦合后的传播常数,β1和β2表示两种非耦合模式的无扰动解,κ 为耦合系数,当损耗腔和增益腔,除损耗外的参数全都相同时,可得

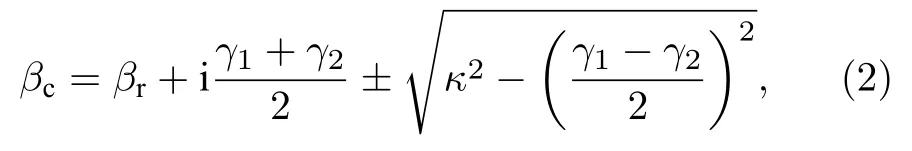
βr为传播常数的实部,显然在PT对称破缺点时,增益损耗 (γ1-γ2)/2 与耦合系数 κ 之间要满足一定的比例关系[25,26],使项带来的虚部刚好为0,当固定损耗增加时,PT对称破缺点对应的增益数值下降.并且破缺点处对应的虚部数值 (γ1+γ2)/2,由于 γ1数值减小以及 γ2的减小(固定损耗增大),也会明显减小.

本文还对器件结构对称性的影响进行了模拟分析,分别模拟了增益区与损耗区长度比例为5∶5,7∶3以及8∶2时的结果,如图6—图8所示.

图6为增益区与损耗区长度比例分别为5∶5,7∶3以及8∶2时的结构图,图7和图8为固定损耗区虚部为–0.05时模拟结果.其中图7为 nIl和波长的关系曲线,图8为 nIl和特征频率虚部的关系曲线.图中,黑线和红线、蓝线和绿线、紫线和棕线分别对应增益区与损耗区长度比例为 5∶5,7∶3 以及8∶2时的发射模式以及吸收模式.由于模拟结构的总长度不变,非对称性的增加,在这里可以理解为损耗腔损耗的减小,增益腔带来的增益与损耗腔带来的损耗 (γ1-γ2)/2 与耦合系数 κ 之间仍然要满足耦合模方程中PT对称破缺点时对应的关系,损耗的减小会导致PT对称破缺点处对应增益的变大,且破缺点处对应的特征频率虚部数值变大.

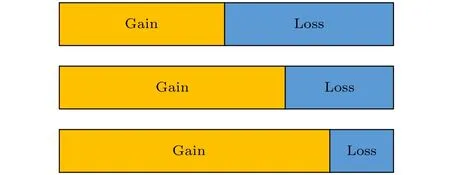
图6 增益区和损耗区长度比为 5∶5,7∶3 以及 8∶2 时的结构图Fig.6.Simulation structure of ridged waveguide when length ratio of gain region and loss region is 5∶5,7∶3,and 8∶2.

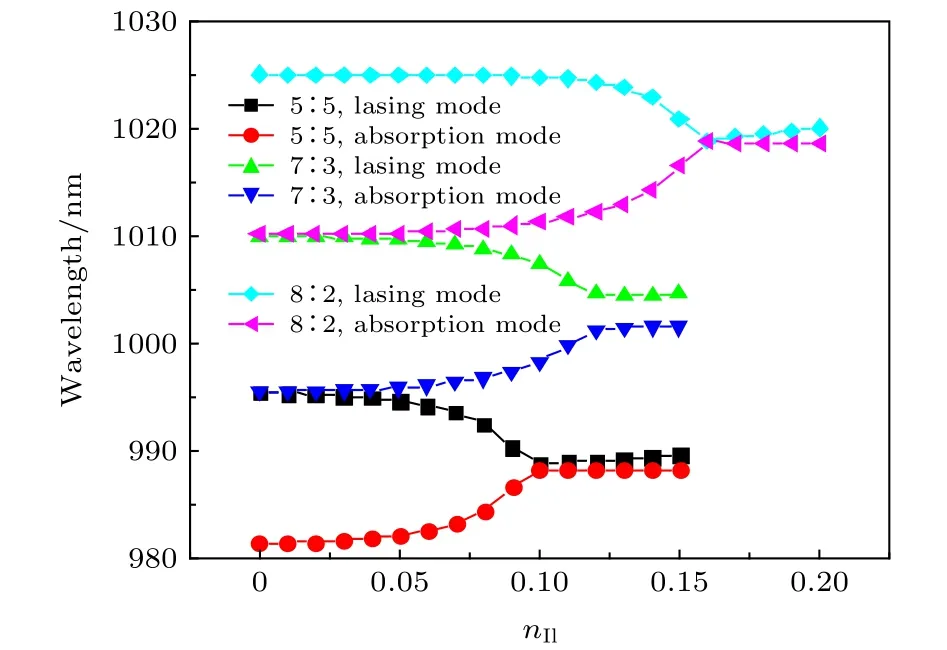
图7 长度比为 5∶5,7∶3 以及 8∶2 时,波长与 nIl 的关系图Fig.7.Relationship between wavelength and nIl when the length ratio is 5∶5,7∶3,and 8∶2.

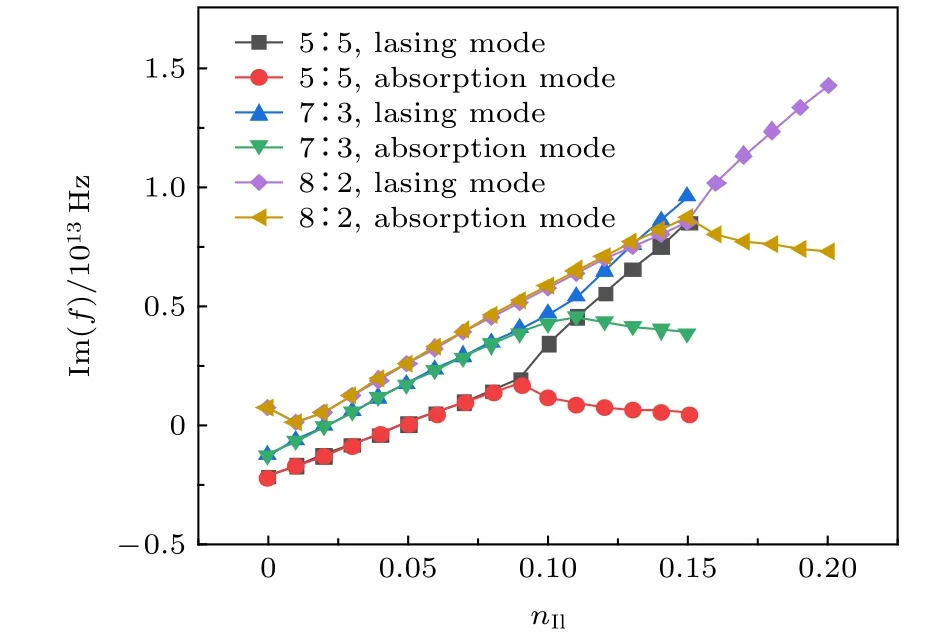
图8 长度比为 5∶5,7∶3 以及 8∶2 时,特征频率虚部与nIl的关系图Fig.8.Relationship between the imaginary part of the characteristic frequency and nIl when the length ratio is 5∶5,7∶3,and 8∶2.

3 实验结果

在激射条件下,通过对注入电流的控制来实现增益的调制,将激光器的输出在热电制冷器(thermoelectric cooler,TEC)制冷的条件下由光纤导入光谱仪中,测试了其腔模(非激射模)与注入电流大小的关系,发现当电流达到PT对称破缺 (约 320 mA) 后,发生模式简并现象,测试结果如图9所示.

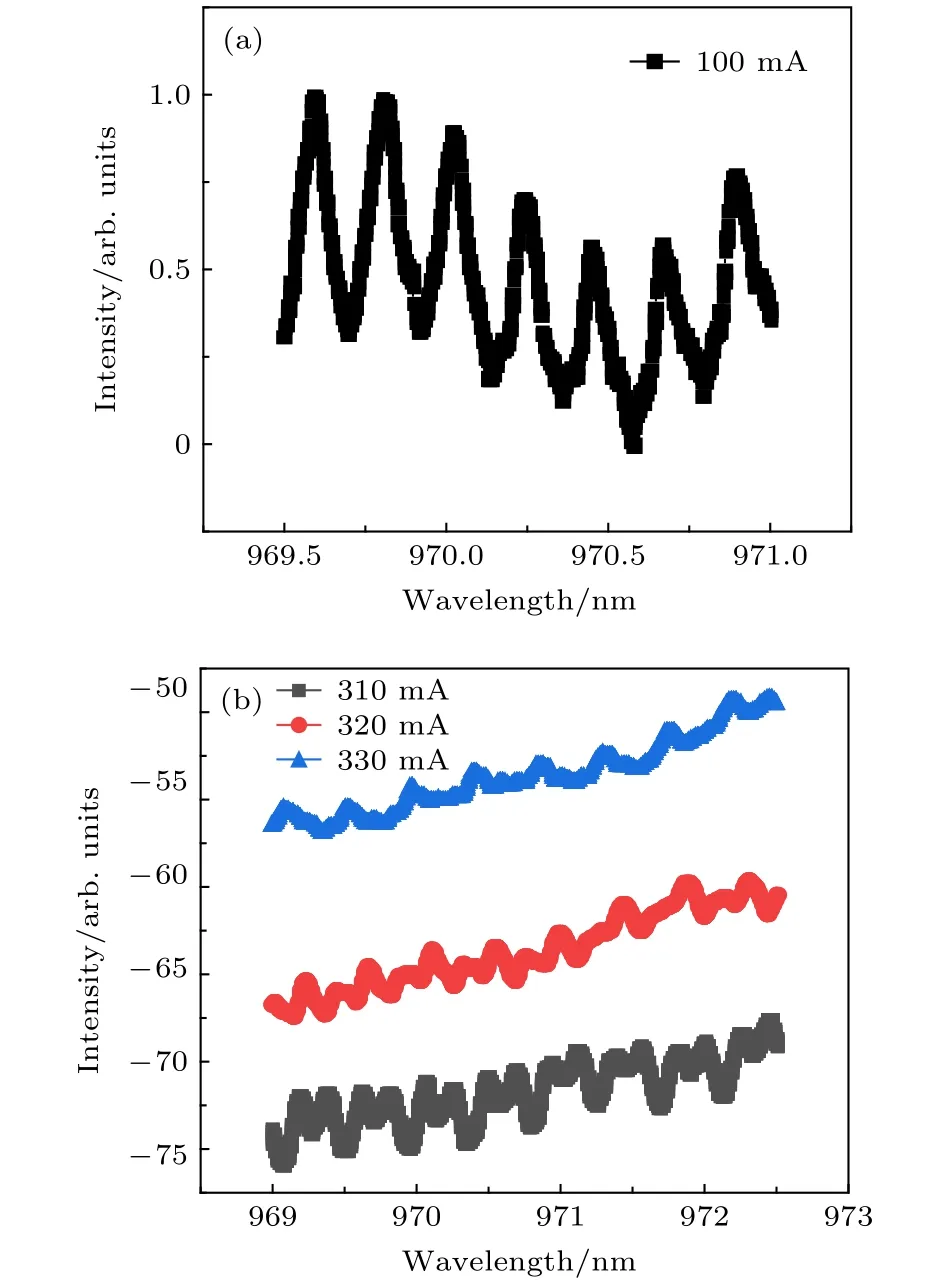
图9 腔模强度与波长关系(a)注入电流为100 mA;(b)注入电流分别为310mA(黑 线)、320 mA(红 线)以及330 mA(蓝线)Fig.9.Relationship between the normalized intensity and wavelength of cavity modes:(a) The injection current is 100 mA;(b) the injection current is 310 mA (black line),320 mA (red line) and 330 mA (blue line),respectively.

由图9(a)可以看到,模式间隔0.24 nm与理论计算数值(Δ λ ≈ λ2/(2nL)=0.25nm)基本匹配.由图9(b)可以明显地发现,在发生PT对称破缺后,腔模模式简并,模式间隔加倍,并且模式数减半.这是因为实验制备器件和模拟都是两个腔(gain腔和loss腔),是两个腔内模式的耦合,PT对称破缺点其实就是传播常数中项虚部刚好为0的点,这就是两个模式简并为一个模式的原因,表现出来的现象就是模式数减半,相应地,模式间隔就会加倍.当腔的个数改变时,有可能实现更高阶的模式简并,比如模式数变为1/3,模式间隔变为3倍或更多的现象[26].

4 结 论

通过模拟分别分析了损耗的大小和非对称性对于PT对称性的影响,发现损耗区固定损耗的增加会导致PT对称破缺点所对应的 nIl数值变小,并且会使破缺点对应特征频率的虚部减小;激光器总腔长不变的情况下,非对称性的增加会导致PT对称破缺点所对应的 nIl数值变大,并且会使破缺点对应特征频率的虚部变大.本文还通过电注入脊条波导实验,观察到了激射条件下,腔模发生PT对称破缺的现象,即腔模的模式间隔加倍以及模式数减半.电注入条件下PT对称性的引入有利于对半导体激光器实现更好的模式调控,并且使PT对称性在小尺寸、复杂结构器件中的实现更为容易.