一种卫星导航接收机固定多波束抗干扰方法

马衍秀，马忠志，李晓东，杨述华

(1.北京遥测技术研究所，北京 100076；2.火箭军装备部驻北京第二军代表室，北京 100076)

0 引言

全球卫星导航系统(Global Navigation Satellite System, GNSS)在军事、商业、民用基础建设中的应用越来越广泛。然而，由于GNSS信号到达地球表面时的功率已十分微弱，很容易受到各种有意或无意的电磁干扰，从而导致接收机接收信号的信噪比下降，定位精度降低，甚至无法捕获跟踪定位[1]。这也使得抗干扰技术成为了卫星导航应用领域的一个研究热点。

自适应天线阵列是一种有效的GNSS抗干扰措施[2-4]。采用功率倒置准则的自适应调零算法已在工程实践中得到广泛应用。自适应调零无需任何先验信息辅助，可通过自适应调整不同天线阵元的加权值在干扰方向形成零陷，工程实现简单，但其在抑制干扰的同时未能对卫星信号进行有效保护，会导致卫星信号存在一定程度上的能量衰减和波形失真。为解决上述问题，进一步提升导航接收机的抗干扰能力，自适应波束形成算法成为了抗干扰技术中的一个重要研究方向[5-6]。自适应波束形成不仅能够在干扰方向形成零陷，还通过在算法中施加卫星导向矢量约束形成指向卫星信号来向的高增益波束，在抑制干扰的同时提高卫星信号信噪比，从而对卫星信号进行有效保护。近年来，虽然自适应波束形成算法的理论研究已较为成熟，但其在工程实践中的应用和推广依然存在诸多问题，主要包括：1)阵列天线、射频通道等硬件平台的通道幅相误差导致波束指向失配，引起抗干扰性能下降[7-8]；2)硬件平台通道幅相误差标定的复杂度高，对标定环境的要求较为苛刻，工程代价较大[9-11]；3)依赖载体姿态、卫星来向等先验信息，鲁棒性不高。文献[7]分析了硬件通道幅相误差对自适应波束形成的性能影响，指出幅相误差可导致波束不能对准卫星信号方向、使干扰零陷深度变浅、输出信干噪比(Signal to Interference plus Noise power Ratio, SINR)下降等问题，需要在工程设计中对幅相误差进行校正。文献[10]采用了一种基于真实卫星信号数据采集后处理的方法进行幅相误差标定，但存在标定耗时长、工程可实现性差的问题。文献[11]提出了一种基于对称阵列单元结构设计的幅相误差标定方法，但该方法忽略了天线阵元的安装误差和方向图不圆度，工程中的标定效果很难保证。文献[12]和文献[13]提出了盲波束形成的抗干扰方法，但大都需要利用卫星信号的循环平稳特性或需要在干扰施加之前捕获卫星信号，当导航接收机在强干扰环境中冷启动时，该类方法将不能快速形成波束，影响抗干扰性能。文献[14]提出了一种无需先验信息的多波束抗干扰方法，但未从理论上分析最优波束的空间分配方式。

针对自适应波束形成在工程实践中存在的问题，本文提出了一种固定多波束形成的卫星导航天线阵抗干扰方法，给出了工程实现架构，分析了最优的波束空间分配方案和卫星筛选定位策略，并通过仿真试验进行了性能验证。该方法无需先验信息辅助，也无需进行复杂的幅相误差标定，可在干扰环境中快速形成多个波束，具有抗干扰性能好、鲁棒性强、易于工程实现等优点。本文安排如下：首先介绍卫星导航天线阵自适应波束形成抗干扰的信号模型，然后对本文所提出的固定波束形成抗干扰方法进行详细的说明，最后进行仿真实验，从而得出本文结论。

1 自适应波束形成抗干扰

考虑一个M阵元的天线阵，假设远场有1个卫星信号s(t)和J个互不相干的干扰信号jp(t)(p=1, 2, …，J)以平面波的形式射入天线阵，则阵列接收信号X(t)可表示为

X(t)=S(t)+J(t)+N(t)

(1)

式中：S(t)、J(t)和N(t)分别为M维的卫星接收信号、干扰接收信号和本地噪声信号；as=[a1,a2,…,aM]T为卫星信号导向矢量，与阵元位置和卫星信号来波方向有关，其中am=e-j2πf0τm(m=1,2,…,M)，τm为第m阵元接收的卫星信号与参考阵元接收的卫星信号的相对时延；同理，ap为干扰信号导向矢量。依据最小方差无失真响应(Minimum Variance Distortionless Response，MVDR)准则，如式(2)所示，将卫星信号方向增益约束为1(单位约束)，且使得阵列的输出功率最小。

(2)

由拉格朗日乘子法，解得MVDR准则的最优权值矢量如式(3)所示

(3)

其中，Rxx=E[X(t)X(t)H]为阵列接收信号的协方差矩阵。

由式(3)可知，通过施加卫星导向矢量约束，可在抑制干扰的同时形成指向该卫星的波束，对卫星信号形成有效保护。在工程实现中，通常采用多个并行的波束形成器分别指向不同的卫星信号，典型的自适应波束形成设计架构如图1所示。

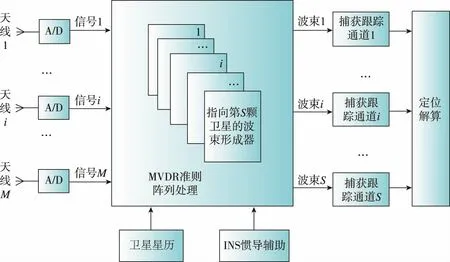
图1 自适应波束形成实现架构示意图Fig.1 The structure of adaptive beamforming algorithm

卫星信号和干扰信号由天线阵接收后，经变频和采样，由模/数转换模块(A/D)将模拟信号转换成数字中频信号，传递给阵列信号处理模块。阵列信号处理模块通过从外界获取卫星位置、载体姿态等先验信息，依据MVDR准则在抑制干扰的同时对每颗卫星信号形成一个波束形成器，并分配给相应的接收机通道进行捕获跟踪，获得伪码、载波相位等信息。

理论上，自适应波束形成虽然可以进一步提升卫星导航接收机的抗干扰能力，但其在具体工程设计和应用中还存在受硬件平台幅相误差影响大、硬件标定复杂度高、依赖先验信息辅助和鲁棒性差等问题，这也进一步限制了自适应波束形成在某些平台和环境中的工程应用。

2 固定多波束抗干扰

针对自适应数字波束形成在工程实现中存在的问题，本文提出了一种固定多波束形成抗干扰方法，设计架构如图2所示。

图2 固定多波束形成实现架构示意图Fig.2 Structure of fixed multi-beam forming algorithm

该方法的核心思想是通过将整个空域分成P个子空间，并指定P个波束形成方向，使每组权值形成的波束中的主波束指向该子空间，从而对多个卫星信号形成增益。然后通过在每个固定波束后连接捕获跟踪通道对卫星信号质量进行筛选，筛选后的优质卫星参与定位解算，从而得到定位结果。

与典型的自适应波束形成抗干扰方法相比，固定多波束抗干扰方法不需要载体姿态和卫星信号来向等先验信息，也无需复杂的硬件误差标定，接收机在冷启动条件下也能快速形成多个波束，具有鲁棒性强、更易工程实现等优点。以下分别描述固定多波束形成的最优波束分配方式和优质卫星筛选方法。

2.1 最优波束空间分配

最优波束空间分配主要从波束个数和波束增益覆盖范围两方面进行考虑。设定一组波束指向初值，包括波束指向个数P和每个波束指向对应的方位角θl和俯仰角φl。如果天线阵型和每个天线单元的方向图确定后，则该天线在每个方向上的波束覆盖范围是可以确定的。因此，可以根据阵列天线的阵型和各天线单元的方向图进行波束扫描仿真，确定整个天线接收空间范围内各方向对应的波束覆盖范围，从而确定波束指向个数和波束指向角度的初值。

对于阵元分布确定的天线阵列，设参考阵元的坐标为原点，第m个阵元的位置坐标为(xm,ym,zm)，m=2,…,M，当该天线阵接收来向为(θ0,φ0)的卫星信号时，所形成的数字波束方向矢量为

a=[1,ej2πf0τ2,…,ej2πf0τM]

(4)

其中，τm为第m个阵元与参考阵元接收信号之间的波程差，其解析式为

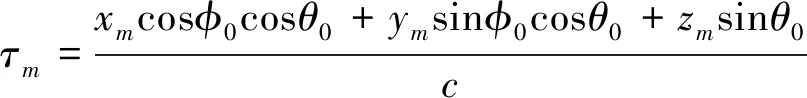
(5)

其中，c为光速，f0为信号中心频率。

当天线阵中各阵元位置固定时，其静态方向图的主瓣宽度固定，由此可得该波束主瓣在方位角方向波束宽度Δθ和俯仰角方向的波束宽度Δφ。

在波束宽度Δθ和Δφ确定的情况下，可以进一步确定波束个数

(6)

其中：θmax和θmin分别为阵列天线接收空间内的最大仰角和最小仰角；φmax和φmin分别为阵列天线接收空间内的最大方位角和最小方位角。

本文以七阵元带参考节点的圆阵为例，详细介绍了最优多波束指向的确定。阵元位置分布如图3所示。

仿真中，将固定波束仰角设定为20°～ 90°，方位角均设定为180°。波束的典型方向性图分别如图4～图6所示，每个固定仰角的波束宽度统计如表1和表2所示。

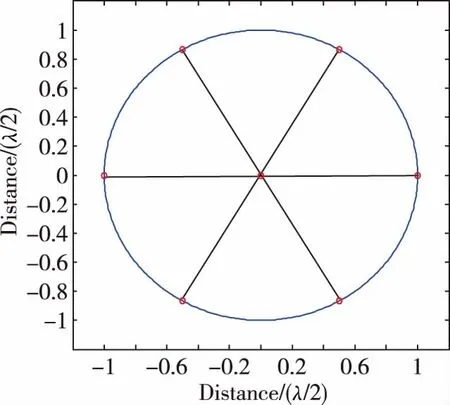
图3 七阵元天线阵元分布示意图Fig.3 Location of seven-array antenna array

图4 波束指向(180°, 30°)的方向图Fig.4 Beam pattern for (180°, 30°)

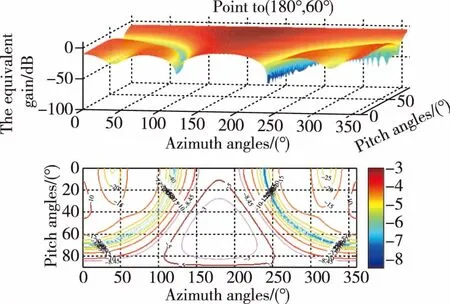
图5 波束指向(180°, 60°)的方向图Fig.5 Beam pattern for (180°, 60°)

图6 波束指向(180°, 90°)的方向图Fig.6 Beam pattern for (180°, 90°)

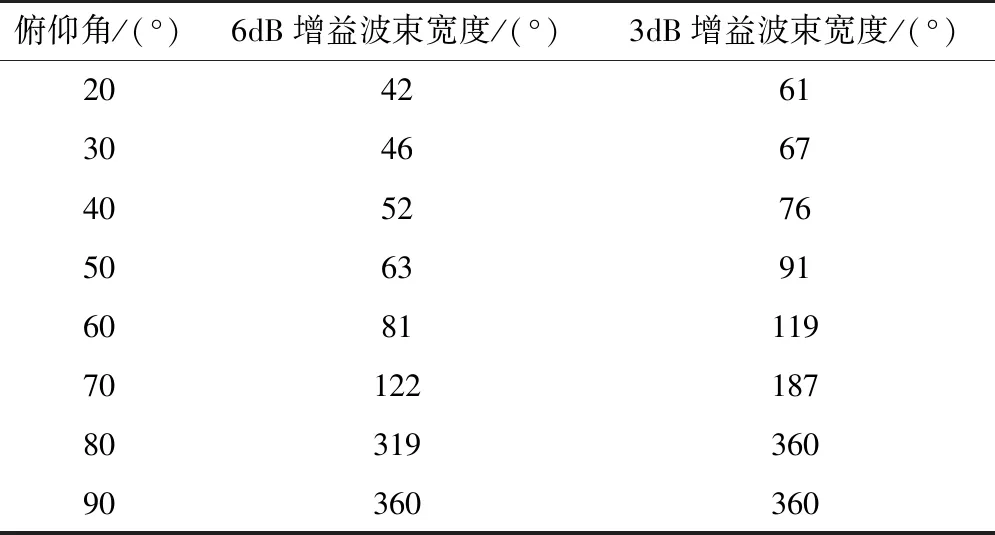
表1 俯仰角方向剖视波束宽度统计结果Tab.1 Statistical results of beam width after pitch angle section

表2 方向角方向剖视波束宽度统计结果Tab.2 Statistical results of beam width after yaw angle section

由表1统计结果可知，沿俯仰角剖视，在不同仰角上设定的固定波束覆盖范围有较大差异，波束仰角越低，波束3dB增益覆盖的方位角范围越小；而波束仰角越高，波束3dB增益覆盖的方位角范围越大。由表2统计结果可知，沿方向角剖视，当波束固定在高仰角时，波束3dB增益覆盖90°以下至某个阈值范围内，且仰角越高，波束3dB增益覆盖范围越小；当波束固定在低仰角时，3dB增益波束覆盖0°以上至某个阈值范围内，且仰角越小，波束3dB增益覆盖范围越小。波束6dB增益的覆盖规律与3dB增益相同。

从卫星分布和抗干扰角度考虑，固定波束指向的仰角不宜过低，从波束增益覆盖范围角度考虑，固定波束指向的仰角不宜过高。因此，在进行固定波束分配时，可以将1个波束指向设定在高仰角90°，剩余波束指向设定在仰角30°～50°范围，以在卫星接收空域内达到较高的波束增益覆盖率。

本文算法设计中，设定6个固定波束，其中1个波束指向仰角90°，另外5个波束仰角均为40°，并在方位角上均匀分布，具体波束指向为(180°, 90°)、(0°,40°)、(72°,40°)、(144°,40°)、(216°,40°)、(288°,40°)。由表1和表2可知，6个固定波束的3dB增益波束覆盖了天线阵列整个上半球空间，6dB增益可以覆盖78.7%的上半球空间。

2.2 优质卫星信号筛选

固定多波束抗干扰将整个空域分为P个子空间，并形成P个波束，每个波束可能会覆盖多颗卫星信号，即，抗干扰处理后P个波束的空域合集中可能含有多个重叠的卫星信号，因此需要对卫星信号进行筛选。

本文提出的方法是在捕获跟踪通道后增加一个卫星信号筛选模块。模块示意图如图7所示。当捕获跟踪到i号卫星时，首先计算该卫星的SNR

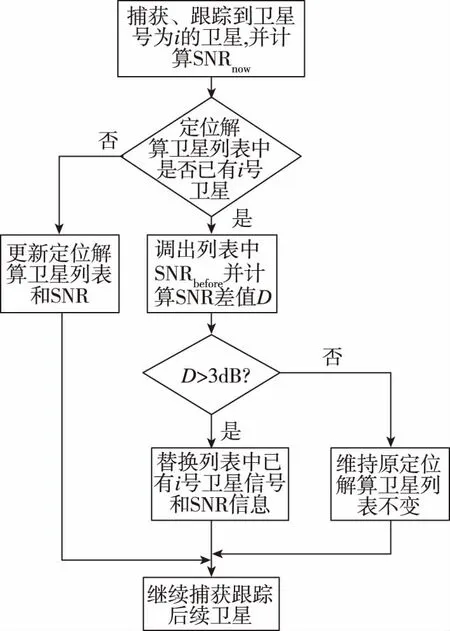
图7 优质卫星筛选流程图Fig.7 Flowchart of choosing high quality satellite

(7)

得到SNRnow，然后判断当前定位解算卫星列表中是否已含i号卫星：如果列表中没有i号卫星，则将当前捕获跟踪到的i号卫星添加到定位解算卫星列表，并更新SNR；否则，调出列表中i号卫星的SNRbefore，计算SNR的差值D

D=SNRnow-SNRbefore

(8)

如果D>3dB，则当前i号卫星取代原定位解算列表中的i号卫星加入定位解算卫星列表，并更新SNRbefore；否则，维持原定位解算卫星列表不变。

以6个波束子空间共收到10颗卫星为例，从6个分集中优选信噪比高的卫星进行定位解算的示意图如图8所示。用圆周代表波束子空间，Sn(n=1,2,3,…,12)代表收到的卫星序列号。子空间P1、P2、…、P6共收到10颗卫星，分别为

•P1：S4、S5、S6、S8；

•P2：S1、S2、S4；

•P3：S2、S3、S6；

•P4：S7、S8；

•P5：S9；

•P6：S8、S10。

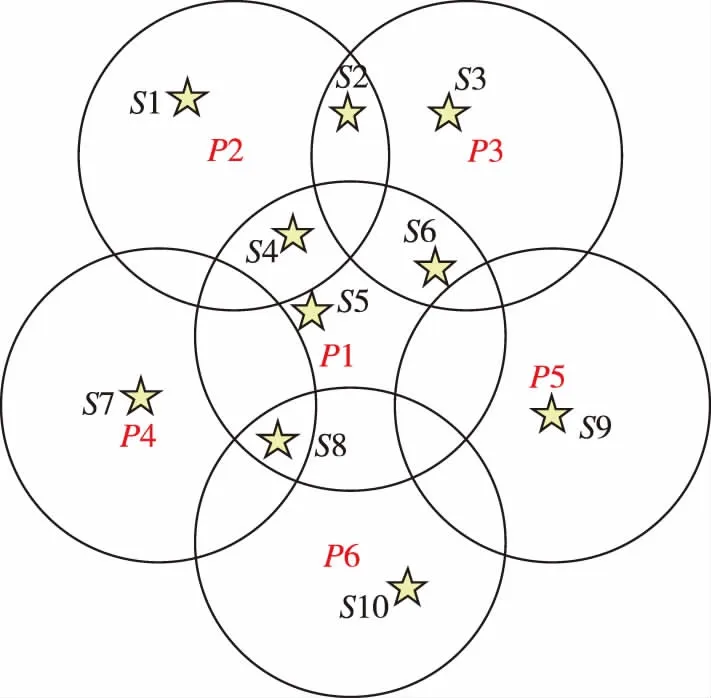
图8 各分集收星示意图Fig.8 Schematic diagram of each diversity receiving stars

依据选星准则，S1、S3、S5、S7、S9、S10直接参与定位解算。而S2、S4、S6、S8均有2个以上(含2个)的波束收到，需要根据信噪比筛选卫星进行后续的定位解算。用Sn_Pm(n=1,2,…,10；m=1,2,…,6)表示子空间Pm收到的Sn号卫星，则最后用于定位解算的卫星为

•S1_P2、S3_P3、S5_P1、S7_P4、S9_P5、

S10_P6；

• MAX_SNR_D{S2_P2,S2_P3}；

• MAX_SNR_D{S4_P1,S4_P2}；

• MAX_SNR_D{S6_P1,S6_P3}；

• MAX_SNR_D{S8_P1,S8_P4,S8_P6}。

其中，MAX_SNR_D表示选取集合中信噪比最高且与其他卫星信噪比差值大于3dB的卫星，如不满足D>3dB条件时，按捕获跟踪顺序选取卫星。

3 性能仿真验证

3.1 仿真条件

为了验证固定多波束方法的抗干扰性能，本文采用基于MATLAB数值仿真的形式将固定多波束(Fixed Multi-Beamforming, FMB)算法与自适应调零算法(PI准则)、典型自适应波束形成算法(MVDR准则)在同一干扰环境进行了性能比较。具体仿真条件如下：

1)天线阵

天线阵沿用第2节图3介绍的带有中心参考阵元的七阵元圆阵，天线阵元间距满足卫星信号半波长要求。

2)卫星信号和干扰信号

选取本地某一时刻真实的GPS可见卫星分布情况作为仿真的卫星星座条件，如图9所示，并针对GPS L1频点设置干扰。干扰信号为宽带高斯噪声干扰，中心频点为1575.42MHz，干扰带宽为2MHz，与卫星信号的带宽相同。带内热噪声为-140dBW，卫星信号信噪比为-20dB，干扰信号的干噪比为70dB。详细参数设置如表3所示。

图9 卫星和干扰位置星座示意图Fig.9 Maps of satellite and jamming

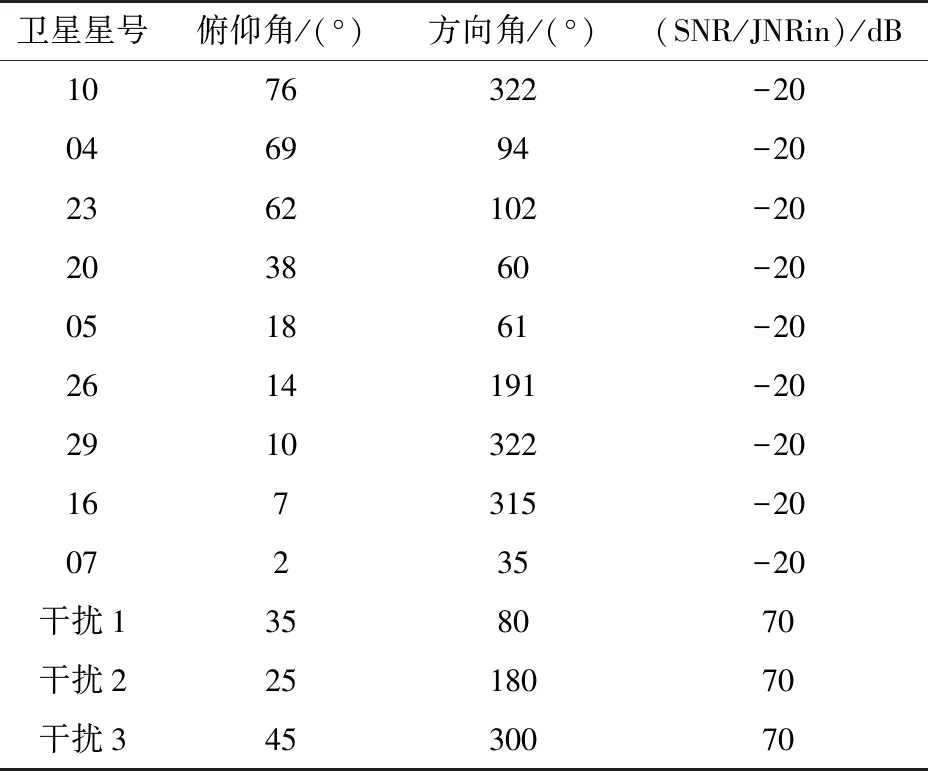
表3 卫星和干扰仿真参数设置Tab.3 Settings of satellite and jamming simulation

3)误差项

实际硬件系统中，误差来源主要包括阵元通道幅相误差和ADC量化噪声。器件发热和老化、天线阵周围环境的变化、阵元天线安装误差、滤波器群延时差异等，都会引起通道幅相特性的变化。ADC分辨率、时钟源抖动等误差都将产生ADC量化噪声。因此，本文仿真中考虑硬件(阵列天线、射频通道)通道幅相不一致误差、ADC量化误差和波束形成指向精度误差。

M自适应天线阵的通道不一致系数矩阵数学模型为[1]

(9)

式中，ρi和ψi分别为第i通道的幅度误差和相位误差，ρi服从高斯分布，ψi服从均匀分布。对于接收天线阵列而言，其阵列流型矩阵为

(10)

式中，A为阵列方向矢量。

相应地，天线阵的输出则变化为[8]

X(t)=ΓΑ[S(t)+J(t)]+N(t)

(11)

式中，N(t)为通道噪声向量。

ADC对输入的模拟信号进行采样和量化，定义ADC最大量化范围为±V，量化位数为NADC，则Δ表示ADC的最小量化间隔，Δ为[14]

(12)

实际工程中，ADC的量化噪声可以通过ADC的有效位数(ENOB)来表征。

MVDR波束指向精度误差服从正态分布N(μ,σ2)，μ为波束指向误差的均值，σ2为波束指向误差分布的方差。

综上分析，本文仿真中的误差项参数设置为：各通道的幅度误差在-3dB～3dB内服从高斯分布，相位误差在-20°～20°内均匀分布；ADC量化位数为16位，有效位数为12位；MVDR波束指向精度误差均值μ分别为5°、10°、15°和20°，方差σ2为1°。

3.2 仿真结果

分别对无误差理想条件下和有误差非理想条件下不同算法的抗干扰性能进行仿真，统计抗干扰处理后卫星信号的SINR。

1)理想条件

理想条件下各算法的抗干扰仿真结果如图10所示。

图10 理想条件下不同算法抗干扰处理后的卫星信号SINRFig.10 Comparisons of SINR after different processing

当抗干扰输出的卫星信号SINR<-30dB时，认为接收机不能正常捕获跟踪到该颗卫星，因此，图10中未画出SINR<-30dB的卫星。从图10中可以看出，PI算法的抗干扰性能最差，MVDR波束形成算法的抗干扰性能最好，本文提出的FMB波束形成算法与MVDR波束形成算法的性能接近。这是因为PI算法在抑制干扰的同时未对卫星信号进行有效保护，当干扰与卫星的空间分布比较接近时，PI算法对卫星信号的能量造成较大衰减。而理想条件下，MVDR波束形成算法可以将波束准确地指向各颗卫星，形成最高波束增益，从而获得最优的抗干扰性能。FMB波束形成算法通过最优波束空间分配使波束增益覆盖到了所有卫星，并筛选信噪比高的优质卫星参与定位解算，从而获得接近MVDR波束形成的次优抗干扰性能。

2)非理想条件

加入硬件通道幅相不一致误差、ADC量化噪声误差和MVDR波束指向精度误差后，各算法的抗干扰仿真结果如图11所示。

如图11所示，在存在通道幅相误差和波束指向精度误差的情况下，PI算法的抗干扰性能依然最差，MVDR波束形成的抗干扰性能随着波束指向精度误差的增加出现下降，特别是20号星和5号星的SINR下降明显，本文提出的FMB算法抗干扰性能无明显下降。表4统计了MVDR波束形成算法与FMB波束形成算法抗干扰处理后输出的同一颗卫星的SINR差值，其中，当MVDR算法处理后的卫星信号信干噪比高时，数值为正，反之为负。

(a)波束指向精度误差5°

(b)波束指向精度误差10°

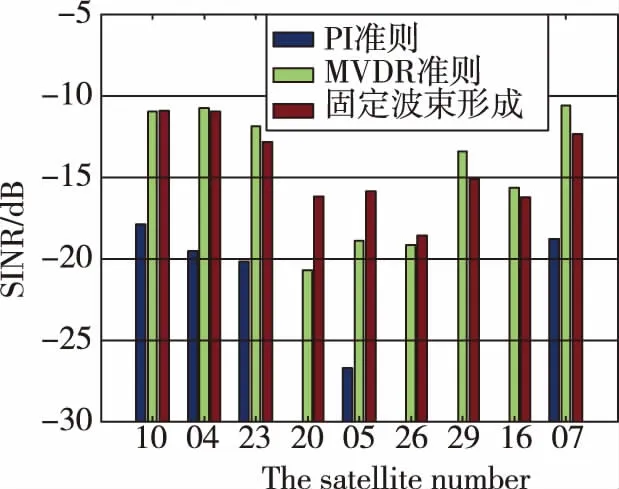
(c)波束指向精度误差15°

(d)波束指向精度误差20°图11 非理想条件下不同算法抗干扰处理后的卫星信号SINRFig.11 Comparisons of SINR after different processing

表4 不同算法处理后信号信干噪比统计表Tab.4 SNR statistical results of signal processed by different algorithms

由表4可知，在存在硬件通道幅相误差的条件下，当波束指向精度误差为5°时，FMB算法抗干扰输出的卫星信号SINR与MVDR算法非常接近，两种算法SINR差值的平均值为1.20dB；当波束指向精度误差为10°时，两种算法的SINR差值进一步缩小为0.77dB，且20号和5号卫星经FMB算法处理后的SINR已高于MVDR算法；当波束指向精度误差为15°时，经FMB算法处理后，有4颗卫星的SINR高于MVDR处理结果；当波束指向精度误差为20°时，FMB算法处理后卫星的SINR高于MVDR算法1.99dB，5颗卫星的SINR高于MVDR算法，特别是20号和5号卫星的SINR差距明显，分别达到11dB和5dB以上。

从仿真结果可以看出，本文提出的FMB波束形成算法在通道幅相不一致误差、ADC量化噪声误差和波束指向误差存在的条件下，可以达到与典型MVDR波束形成算法相当的抗干扰性能。在波束指向精度误差为20°的恶劣条件下，固定多波束方法的抗干扰性能更优，对SINR的性能改善最高达到11dB，平均改善1.99dB。相对于MVDR算法，FMB算法具有更好的抗干扰鲁棒性，更易于工程实现。

4 结论

典型的自适应波束形成技术在工程实现中依赖卫星来向、载体姿态等先验信息，受硬件通道幅相误差和波束指向精度误差的影响较大，且硬件标定复杂度高。针对这一问题，本文提出了一种固定多波束卫星导航接收机抗干扰方法，并给出了最优的波束空间分配方案和卫星筛选定位策略。该方法无需先验信息辅助和复杂的硬件误差标定，鲁棒性强且更易工程实现。性能仿真验证结果表明：在实际工程误差存在的条件下，本文提出的固定多波束抗干扰方法性能与典型的自适应波束抗干扰方法性能相当。在波束指向精度误差为20°的恶劣条件下，固定多波束方法的抗干扰性能更优，对SINR的性能改善最高达到11dB，平均改善1.99dB。