基于冗余伪观测的自适应滤波算法

蒋刘洋，张 海

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

0 引言

经典的卡尔曼滤波要求在确定的系统模型和观测方程下，对系统噪声和量测噪声的统计特性具有准确的先验知识[1]，因此噪声分布在卡尔曼滤波器的状态估计中起着非常重要的作用。然而在多数实际应用中，噪声的统计特性通常是未知的，往往被经验值替代；此外还会因为受到环境等因素的影响而发生改变。上述情况都会使预设的噪声方差不能准确地反映当前系统模型的随机噪声特性，导致估计精度下降，甚至滤波器发散。自适应滤波是一种具有抑制滤波器发散作用的方法，其在滤波计算过程中，同时对未知的或不确切的系统模型参数和噪声统计参数进行估计和修正。自适应滤波方法有很多，从滤波器结构的角度划分，大体上可分为两类：基于多模型的自适应估计(Multiple Model Adaptive Estimation，MMAE)和基于新息/残差的自适应估计(Innovation-based Adaptive Estimation，IAE/Residual-based Adaptive Estima-tion，RAE)[2-3]。

MMAE是由Magill于1965年提出的[4]，当系统模型未知或不确定时，该方法仍能给出较准确的状态估计结果。标准的MMAE滤波器同时运行一组卡尔曼滤波器，其中的每个滤波器使用不同的系统动态模型或随机噪声模型，然后基于Bayes方法通过新息或残差计算每个模型是正确模型的概率，最后对每个滤波器的输出结果做加权和得到最优的状态估计[5-6]。在实际应用中，当系统模型由于某些未知原因发生变化时，该方法仍能给出较高精度的状态估计结果，因此，故障诊断是其最具潜力的应用领域之一[7-8]。

IAE/RAE方法是对经典卡尔曼滤波方法的一个扩展，通过额外的程序对过程噪声方差矩阵与观测噪声方差矩阵进行自适应估计和调节，使其不断地适应系统的变化[9]。近年来，IAE/RAE算法取得了很多新的进展：文献[10]提出了一种使用新息向量及其滞后时刻向量的自协方差函数来估计过程噪声方差矩阵与观测噪声方差矩阵的最小二乘回归法。文献[11]提出了一种具有鲁棒性的抗差自适应卡尔曼滤波(Robust Adaptive Kalman Filtering，RAKF)算法，RAKF利用一个自适应因子来调节状态预测误差的协方差矩阵。该自适应因子是通过比较实际的新息协方差矩阵与其对应的理论值来计算获得的，且其值大于1，故RAKF为新的量测值提供了更多的权重，增强了滤波器的鲁棒性。文献[12]基于Sage-Husa自适应滤波,引入改进的时变噪声估计器实时估计噪声的统计特性。此外，文献[13]基于新息和残差的相关性推导出了一个包含过程噪声协方差的线性矩阵方程，从而实时解决过程噪声方差矩阵。

值得注意的是，上述几种算法都是基于新息和残差向量完成的自适应调节，但是作为数据基础的新息/残差向量耦合了状态量的估计误差。因此，当状态估计误差较大时，调节因子的计算会受到影响，进一步影响到系统噪声方差阵或状态误差协方差阵的估计和调节，从而导致滤波器输出的不准确甚至发散[14]。

为了克服这一问题，有学者提出了基于冗余测量的二阶互差分(Second Order Mutual Difference，SOMD)算法来估计观测噪声方差矩阵[15-16]。该算法的主要思想是利用一个观测序列作为参考来估计另一个观测序列的观测噪声方差矩阵，获得的噪声方差矩阵只与测量系统自身相关，而与滤波系统的其余参数无关，因此与状态估计误差解耦。在此基础上，文献[17]研究了同时估计两种观测系统噪声方差矩阵的算法。然而，由于成本的约束，多数实际系统不能满足冗余测量的前提条件，限制了该算法的应用。

考虑到SOMD算法的优越性，为了避免冗余测量条件的限制，本文通过构建伪测量序列，将SOMD算法扩展到只具有单一测量系统的应用中，使其适用于更广泛的应用场景。

1 SOMD算法简介

本节介绍了一种基于冗余观测利用SOMD序列估计观测噪声方差阵的算法[15]，其主要思想是当被观测对象存在2个不同的观测系统时，根据测量序列的变化关系，分别计算2个序列的一阶自差分序列以及SOMD序列，并通过统计的方法获得观测系统的噪声统计特性。

针对如下描述的线性随机离散系统

Xk=Φk,k-1Xk-1+Wk-1
Zk=HkXk+Vk

(1)

式中，Xk为系统状态；Φk,k-1为状态转移矩阵；Zk为量测量；Hk为量测矩阵。Wk-1为过程噪声，Vk为量测噪声，且有

(2)

式中，E[]为数学期望算子；δkj为Kronecker-δ函数。

SOMD算法具体如下：

(3)

构造2个测量系统的一阶自差分序列以及SOMD序列如下

(4)

如果2个测量系统的精度存在极差，即

(5)

那么方差较大的噪声方差为

(6)

SOMD算法主要有如下特点：

1)测量系统的确定性误差通常在短时间内比较稳定，通过求取一阶自差分序列可将其消除。

2)被测对象在短时间内有可能存在状态突变的现象，在一阶自差分序列中不能被消除，但是SOMD序列可将其完全抵消掉，进而只保留随机噪声项。这也是该方法最突出的特点。

3)与传统的自适应滤波方案不同，SOMD算法将噪声估计作为一个独立的问题进行研究，脱离了对滤波系统的依赖，实现噪声估计与滤波状态估计的解耦。因此，该方法对噪声特性估计的鲁棒性更强。

但是，定理1要求具有冗余测量系统，并且2个测量系统的精度之间存在极差，限制了其应用。若要将定理1扩展到单一测量系统，必须提供一个额外的观测系统作为冗余观测，并且确保其噪声是与直接观测系统的测量噪声不相关的白噪声。

2 基于伪观测的SOMD算法

2.1 基于伪观测的噪声方差矩阵的估计

在本节中，提出了一种构造伪观测的方法，并利用伪观测在SOMD算法的基础上给出了观测噪声方差矩阵的估计(PSOMD)。

定理2.对于线性离散随机系统(1)，定义相邻2个时刻的伪观测以及其一阶自差分序列如下

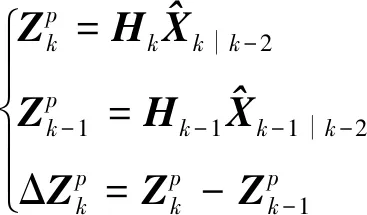
(7)

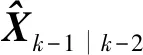
如果采样时间Ts比较小，那么单一测量系统的观测噪声方差可以通过式(8)获得

(8)

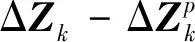
证明：根据系统(1)，直接观测的一阶自差分序列为

ΔZk=Zk-Zk-1

=(HkXk+Vk)-(Hk-1Xk-1+Vk-1)

(9)

(10)

(11)

那么伪观测的一阶自差分序列为

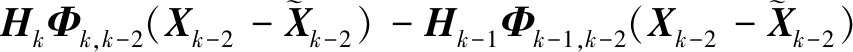
=HkΦk,k-2Xk-2-Hk-1Φk-1,k-2Xk-2-

=Hk(Xk-Φk,k-1Wk-2-Wk-1)-Hk-1(Xk-1-

(12)

式中

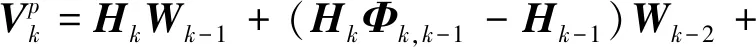
(13)

结合式(9)，可得如下SOMD序列

(14)

(15)

因此

(16)

对于时不变系统，Hk=Hk-1。一般而言，Hk≈Hk-1在较短的时间间隔内也成立，因此式(13)可以简化为

(17)

Pk-2[Hk(Φk,k-1-I)Φk-1,k-2]T

(18)

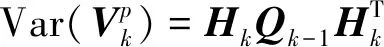
(19)

将式(19)代入式(16)中，可以得到式(8)。定理得证。

由式(19)可知，状态估计误差的影响在伪观测的一阶差分序列中可以忽略，利用伪观测估计的噪声方差矩阵的准确性只与系统的过程噪声方差矩阵有关。在已知过程噪声方差的先验知识的情况下或存在模型补偿时，上述算法的准确性可以得到保障。

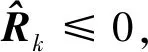
注2：由于经典的IAE自适应滤波算法中，观测噪声方差矩阵的估计中也包含减法运算，其公式为

(20)

(21)

(22)

由式(22)可知，相对于IAE自适应滤波算法，本文所提算法更不容易产生非正定的观测噪声方差估计，也就是说，其计算稳定性优于IAE算法。

2.2 PSOMD算法的实现

在实际应用中，使用整体数据作为样本会造成体现噪声分布变化的动态信息淹没于大量的历史数据中。为了及时适应噪声的变化，以连续滑动开窗的方式，利用当前窗口长度内的数据进行估计，具体如下

(23)

式中，w为滑动窗口的长度。

此外，为了抑制滑动窗口样本不足的影响，采用衰减记忆的方法，引入一个遗忘因子对历史信息进行加权，具体实施如下

(24)

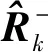
此外， 所提算法对观测噪声方差矩阵的估计效果与采样频率密切相关，采样频率越高，获得的估计精度越高。由于较高的采样频率对计算机的要求也较高，工程应用时可首先尝试采用能够满足要求的低采样频率。

3 仿真验证

在本节中，采用目标跟踪问题作为应用来验证所提算法的有效性，并且通过与扩展卡尔曼滤波(Extended Kalman Filter，EKF)、RAE以及RAKF算法的比较来证明所提算法的有效性。

考虑在3D笛卡尔坐标系中具有直线运动和机动运动的目标轨迹。总的跟踪时间为140s，前50s目标以恒定的速度200m/s做直线运动，50s～100s之间以相同速度做周期为100s的匀速圆周运动，最后仍以200m/s的速度沿直线飞回，目标轨迹如图1所示。

图1 目标运动轨迹Fig.1 Target trajectory

采用三维位置和速度组成系统状态，建立连续的定常速度的运动模型系统，其过程噪声的功率谱密度为

(25)

使用雷达观测距离、俯仰角和方位角，观测周期Ts=0.1s。为了验证所提算法的效果，将观测噪声方差设置为

(26)

由于RAE算法也自适应地估计噪声方差矩阵，故将其与所提算法获得的噪声方差矩阵作对比，结果如图2～图4所示。 由图可知，RAE给出的噪声方差估计在机动运动时段严重偏离真值，这是由于其依赖于状态估计误差导致的误差累积造成的。然而， PSOMD几乎能够在整个跟踪时段给出较准确和稳定的估计(除了噪声方差突然变大之后的过渡阶段，这是由采样频率较低引起的，增大采样频率即可解决)。

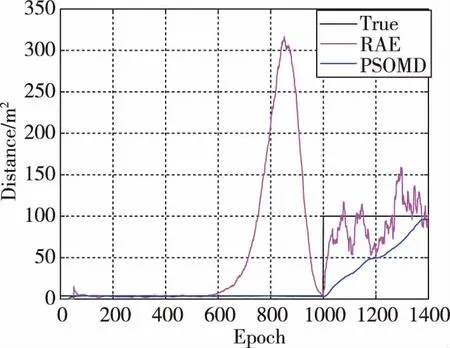
图2 距离的噪声方差估计Fig.2 Estimation of R on distance

图3 方位角的噪声方差估计Fig.3 Estimation of R on azimuth

图4 俯仰角的噪声方差估计Fig.4 Estimation of R on pitch

所有参与比较的自适应滤波算法的位置估计误差如图5和图6所示。结果表明，所有算法给出的估计结果在前50s没有明显的差异，这是因为在该时间段内直线运动的模型准确，观测噪声也没有发生突变。然而，在50s后几种算法之间产生了明显的差异：RAE在目标机动运动期间表现最差，这是因为其基于残差序列并且与状态估计误差耦合；RAKF通过膨胀估计误差协方差可以补偿模型误差，故在50s～100s之间模型不准时给出了误差较小的估计，可是由于其依赖观测使得估计结果比较振荡，尤其是在100s之后观测噪声方差变大的时段；然而，本文所提的算法在整个跟踪时段都给出了比其他算法更准确的估计。

表1列出了连续进行100 次Monte Carlo仿真实验，所有算法在不同的运动模式下的均方根误差(Root Mean Squared Eerrors，RMSEs)。误差数据也表明了所提算法的有效性。

图5 X轴速度误差Fig.5 X-axis position errors

图6 Y轴位置误差Fig.6 Y-axis position errors

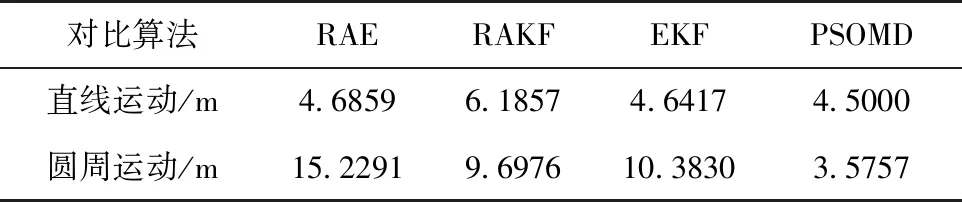
表1 位置估计的误差Tab.1 Average RMSEs of position estimation

表2比较了几种算法的仿真时间。由表2可知，RAE和PSOMD比RAKF和EKF用时较长，这是因为这两种算法都采用了滑动开窗来估计当前时刻的观测噪声方差；而本文所提算法相较于RAE又用时稍长0.01s，这是因为PSOMD为了抑制滑动窗口样本不足的影响采用了衰减记忆的方法。

表2 仿真时间Tab.2 Simulation time

针对目标做螺旋运动的轨迹，在相同的采样频率下进行了仿真实验。结果表明， PSOMD算法仍能给出较准确的滤波结果。由于该算法是基于滑动窗口实现的，如果轨迹更为机动，可以通过提高采样频率来实现快速跟踪。

4 结论

本文介绍了一种基于冗余伪观测的自适应卡尔曼滤波算法来估计观测噪声的方差，并且通过目标跟踪问题验证了该算法的有效性。对本文工作的总结如下：

1)通过构建伪测量将现有的SOMD算法推广到只具有单一测量的系统中，使其适用于更广泛的应用场景。

2)仿真结果表明，即使在采样频率较低时，所提算法仍能够准确反映测量系统的噪声特性，在准确性和鲁棒性方面优于其他参考算法。

3)所提算法对观测噪声方差矩阵的估计中包含了过程噪声方差矩阵。虽然当采样周期较小时，估计结果受状态估计误差的影响可以忽略，但仍受过程噪声方差的影响。只有过程噪声方差确切已知时才能准确地估算观测噪声方差，这使得该算法的应用受到了限制。因此，找到一种方法使过程噪声方差对观测噪声方差估计的影响也可以被忽略，值得进一步研究。