非线性波动方程的新数值迭代方法*

曹娜 陈时 曹辉 王成会 刘航

(陕西师范大学物理学与信息技术学院, 陕西省超声学重点实验室, 西安 710119)

提出了一种新的求解非线性波动方程的数值迭代法, 它是一种半解析的方法.与完全的数值计算方法(如有限元、有限差分法)相比, 这种迭代法的解具有非常清晰的物理含义, 即它的解是各阶谐波的组合.与微扰法相比, 它能够考虑各阶谐波的相互作用, 且能够满足能量守恒定律.用它研究了非线性声波在液体中的传播性质, 结果表明, 在微扰法适用的声强范围内迭代法也适用, 在微扰法不适用的一个较宽的声强范围内迭代法依然适用.

1 引 言

非线性声学是声学的一个重要分支, 当系统的声强比较强时就会产生各种非线性效应, 如谐波产生、冲击波形成、声辐射力的出现等.非线性声学在某些领域有着重要的运用, 如高声强聚焦超声[1−4]、超声悬浮[5−7]、声空化[8]、声谐波成像[9,10]、参量发射阵[11,12]等.在这些领域中声波的非线性方程的求解是非常重要的.

关于非线性声学系统波动方程的求解, 现阶段用到的方法一般包括：1)完全的数值计算方法, 如有限元和有限差分法[13−17].这类方法得到解的物理意义并不明确, 很难揭示非线性作用的物理本质, 而且在很多情况下还会引起数值发散问题, 并非适用于全部的非线性问题.2)严格的解析方法[18−21].这种方法只能处理极少数系统的非线性声学问题,如理想流体中非线性声波的传播.3)微扰法[22].它的优点是方法简单和解的物理意义清晰, 但是只适合处理低声强时的非线性效应.且它只考虑低阶谐波对高阶谐波的作用, 而忽略其反作用, 因此并不满足能量守恒定律.

对于声学非线性方程的求解问题, 本文提出了一种新的、半解析的数值迭代方法.它是在频域内把声场展开为傅里叶级数的形式, 实现时间变量和空间坐标的分离.然后根据计算精度的具体需求,截断高频谐波而实现方程的求解.它的解具有非常清晰的物理意义, 即是各阶谐波的组合.经过研究发现, 在微扰法适用的声强范围内, 本文提出的方法也是适用, 且满足能量守恒定律(无耗散的系统).在微扰法不适用的一个较宽的声强范围内, 迭代法依然适用且满足能量守恒定律(无耗散的系统).只是在极高声强的情况下, 本文提出的方法才不适用.

2 理论方法

2.1 非线性波动方程的迭代数值方法

在拉格朗日坐标系下, 黏性液体中一维非线性声波的位移满足下式[23]：

式中 β 为液体的非线性系数; c0是静态时(即不存在声波时)液体的声速;其中 µ 为液体的体积黏滞系数, ρ0是静态时(即不存在声波时)液体的密度.下标中逗号后的坐标x和时间t表示对它们求偏导数.令 µ =0 , 则方程(1)退化为理想液体中一维非线性声波的波动方程.

在许多情况下(如求解稳态问题), 把u中的变量t和x分离开来是有利的, 一般情况下u可以表示为(可以称为频域内的傅里叶级数展开)：

其中i是一个虚单位, ω 表示波的角频率; A0为一个实数场变量, A0/2 表示声波的“直流”部分;An(n≥1)为第n阶谐波的复数场变量(即复振幅),Anexp(inωt)的实部是第n阶谐波真实的位移,是 An的复数共轭场变量.注意 An和中已经不包含时间变量t, 它们只是空间坐标x的函数.

一般情况下高阶谐波是比较弱的, 根据计算精度的需要可以忽略掉某些高阶谐波.为了简化理论的叙述, 本文只考虑阶数小于或者等于N(N≤6)的各阶谐波, 忽略掉其他的高阶谐波, 称之为N阶近似.

将方程(2)代入方程(1)中, 因为有相同时间因子( e xp(inωt) , n =0,±1,±2,··· )的项之和必须为零, 所以可以得到下面的方程：

注意此处只给出了场变量的方程, 共轭场的方程并没有列出来, 只要对方程(3)—(9)取复数共轭就可以得到共轭场的方程, 因此方程(3)—(9)是完备的.

方程(3)—(9)是一组耦合的非线性方程, 直接求解它们是很困难的.本文提出求解它们的一种新的简单迭代方法.用 A(m)和 A∗(m)( m ≥0 )表示第m次迭代计算得到的场量.在第m次迭代计算中,采用了如下方法：方程(3)—(9)等号左边的场量取为 A(m), 右边的场量取为 A(m-1)和 A∗(m-1).在第m次迭代计算中, 用到如下的方程：

分别用 A(m-1)和 A∗(m-1)替换F中的A和 A ∗ , 得到的结果就是 F(m-1).方程(17)—(23)是一组非耦合的方程, 因此可以分别独立地计算出.这意味着当涉及到更多的高阶谐波时, 计算量不会急剧地增加.

2.2 本文迭代方法的具体运用过程

用迭代方法研究非线性声波在黏性液体中的传播问题.现设在 x =0 处有一列平面波朝x正向传播, 其为入射声波, 且声场可以表示为

其中 Bi是一个已知量.入射波的能流密度 Pi可以表示为

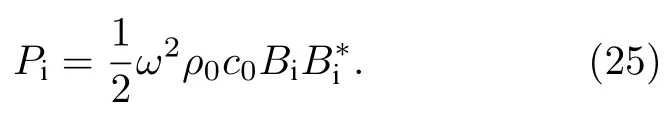
本文需要计算在 x =L 处出射的各阶谐波的声场.它们可以表示为

其中 Bon就是要计算的量.出射波的能流密度Pon可以表示为

为了求解在 [ 0 ,L] 坐标间隔内的非线性声场,用有限差分法来求解方程(17)—(23).在迭代计算中, 令 A(0)=0 和 A∗(0)=0 , 非 零的 A(m)和A∗(m)由边界激励条件产生.用到的边界条件是：在x=0和 x =L 两个端点处, 各阶谐波的位移和垂直应力都是连续的.

3 数值计算和讨论

通过数值计算分析了非线性声波在液体中的传播性质, 得到了本文提出的新数值方法的适用范围, 并证明了其有效性.在所有的计算中, 如果没有特别说明, 那么用到的参数是：c0= 1.5 ×103m/s, ρ0= 103kg/m3, P0= 1.01 × 105Pa,µ=1× 10—3Pa/s, L =0.05 m, ω = 5 × 106rad/s,β=3.5.如果文中或图中对某个参数有特别说明,那么该参数就替换为特殊说明处的数据.

图1显示了非线性声波在理想液体( µ =0 )中传播时能量守恒的破坏程度 Ed、二阶谐波的相对能流 P2/Pi和三次谐波的相对能流 P3/Pi随入射能流 Pi的变化情况.能量守恒的破坏程度 Ed定义为所有出射能流密度与入射能流密度的相对差值,即越小能量守恒越能保证, 它越大能量守恒定律破坏程度越大.实线对应着本文提出的迭代法的情况, 虚线对应着微扰法的情况.

由图1(a)可见, 能量守恒的破坏程度 Ed随入射波能流 Pi的增大而增大.其他参数不变, 入射波能流相同时, 明显可以看出本文提出的新数值迭代方法得到的能量守恒的破坏程度比微扰法得到的能量守恒的破坏程度小很多.当入射波能流是1.5×107J/(m2·s)时, 迭代法的破坏程度是 7.7 ×10—3, 微扰法的破坏程度是 0 .506 ; 当入射能流是5.5×107J/(m2·s)时, 迭代法的破坏程度 1.92 ×10—2, 微扰法的破坏程度是 2 .268 .

由图1(b)和图1(c)可知, 二次谐波的相对能流 P2/Pi和三次谐波的相对能流 P3/Pi均随入射能流 Pi的增加而增加.当入射波能流小于1.5×107J/(m2·s)时, 迭代法和微扰法得到的P2/Pi和 P3/Pi的值几乎相同; 当入射波能流大于5.5×107J/(m2·s) 时, 迭代法和微扰法得到的 P2/Pi的值分别等于 0 .6295 和 1 .4741 及 P3/Pi的值分别大于0.0421和 0 .4847 .

从图1还可以看出, 当入射波能流小于1.5×107J/(m2·s)时, 两种方法(本文提出的新数值迭代法和微扰法)均适用; 当入射波能流小于5.5×107J/(m2·s)且大于 1 .5× 107J/(m2·s)时, 迭代法适用, 微扰法不适用; 当入射波能流大于5.5×107J/(m2·s)时, 两种方法均不适用.

图2显示了声波在理想液体( µ =0 )中传播时各阶谐波的相对能流 Pn/Pi(n=1,2,···,6) 随入射波能流 Pi的变化情况.从图2可见, 各阶谐波的能流随入射波能流的变化趋势相同, 均随入射波能流的增加而增加, 但基频波的能流明显大于其他高阶谐波的能流.从图2还可以看出, 基频波的相对能流随入射波能流的增加而减小, 高阶谐波的相对能流随入射波能流的增加而增加.

图2 各阶谐波的相对能流随入射波能流的变化Fig.2.Relation between relative energy of each order of harmonics and incident wave energy.

图2显示的结果是与文献[20, 24]中基频波能流与各高阶谐波能流之间的关系相一致.从图2可以明显得到, 声波在介质中传播时, 基频波能流向各高阶谐波传递, 这同时也解释了, 基频波的相对能流随入射波能流的增加而减少, 但各高阶谐波的相对能流却随入射波能流的增加而增加.

图3显示了声波在理想液体( µ =0 )中传播时入射波能流不同的情况下二阶谐波的相对能流 P2/Pi随迭代次数m的变化关系.m表示迭代次数.由图3可知, 当入射波能流是0.4687×107J/(m2·s), 迭代次数大于等于3时, 二次谐波的相对能流收敛于 0 .145 ; 当入射波能流是2.7×107J/(m2·s), 迭代次数大于等于4时, 二次谐波的相对能流收敛于 0 .515 ; 当入射波能流是5.418×107J/(m2·s), 迭代次数大于等于 7时, 二次谐波的相对能流收敛于 0 .639 .由图3可见, 本文提出的新数值迭代方法具有收敛性, 且入射声强越大, 达到收敛的迭代次数需要越多.

图3 入射波能流不同时二阶谐波的相对能流随迭代次数的变化Fig.3.Relative energy flow of the second harmonic varies with the number of iterations under different incident wave energy flow.

图4 黏度不同的情况下, 各阶谐波的能流随入射波能流的变化(图中曲线的黏度分别是 1 ×10-6 , 6 ×10-1 和 1 0×10-1 Pa/s,箭头表示黏度减小的方向)Fig.4.Relation of relative energy flow of each order of harmonics with incident wave energy flow under different viscosity.Viscos−ites for different curves are 1 ×10-6 , 6 ×10-1 , 1 0×10-1 Pa/s, respectively.Arrows indicate the direction of decreasing viscosity.

图5为声波在黏性液体( µ =0 )中传播时, 黏度不同的情况下各阶谐波的相对能流 Pn/Pi(n =1, 2)随角频率的变化.从图5(a)和图5(b)可见：1)基频波的相对能流随角频率的增加而减少, 二次谐波的相对能流随角频率的增加而增加; 2)随黏度的增加基频波和二次谐波的相对能流均减小,但基频波的影响程度比二次谐波的影响程度更大一些.

图5 黏度不同的情况下, 各阶谐波的相对能流随角频率的变化(图中曲线的黏度分别是 1 ×10-6 和 1 ×10-1 Pa/s,箭头表示黏度减小的方向)Fig.5.Relative energy flow varies with angular frequency under different visco−sity.Viscosites for different curves are 1×10-6and 1 ×10-1 Pa/s, respectively.Arrows indic−ate the direction of decreasing viscosity.

4 结 论

用一种新的数值计算方法研究了声波在液体中的传播特性.得到的主要结论如下：

2)声波在介质中传播时, 基频波的相对能流随入射波能流(或角频率)的增加而减少, 但各高阶谐波的相对能流却随入射波能流(或角频率)的增加而增加;

3)声波的各阶谐波能流(或相对能流)均随黏度的增加而减小;

4)在相同的参数下, 本文提出的研究计算方法比微扰法能更好地保证在研究声传播的过程中能量守恒, 且当涉及到更多的高次谐波时, 用本文提出的数值方法计算时间不会急剧增加.