基于项目拟合统计量RMSEA的Q矩阵估计方法
杨亚坤 朱仕浩 刘芯伶


摘 要 Q矩阵在认知诊断评估中至关重要,Q矩阵可以由相关领域的专家界定,也可以根据学生的作答数据进行估计。在已有Q矩阵修正方法的基础上,研究提出了基于项目拟合统计量RMSEA的Q矩阵估计方法,通过模拟和实证研究验证了该方法的可行性、有效性及效率。结果表明:(1)基于RMSEA的CSE算法可以有效地估计新题的属性向量,且耗时较少;(2)对Q矩阵估计的成功率受属性数目和基础题个数影响甚大,尤其是当属性数目较多时,要求有较多的基础题个数;(3)该统计量对被试数量要求不高,即使被试人数为400人,只要基础题个数足够多,估计效果依然较好;(4)该方法应用于实证数据的分析,可以一定程度地优化已有的分析结果,提高模型-数据的拟合性。
关键词 认知诊断;Q矩阵估计;项目拟合统计量;DINA模型
分类号 B841.2
DOI: 10.16842/j.cnki.issn2095-5588.2020.01.007
1 引言
在认知诊断评估(Cognitive Diagnostic Assessment, CDA)中,Q矩阵表征了题目与认知属性之间的关联,是认知诊断测验编制的蓝图。Q矩阵直接关系着诊断测验的质量,并最终影响着诊断分类的精确性(涂冬波, 蔡艳, 戴海琦, 2012; Chiu, 2013; de la Torre, 2008; de la Torre & Chiu, 2010; Kunina-Habenicht,Rupp & Wilhelm,2012; Rupp & Templin, 2008)。
在CDA实践中,可以通过采用多种方法,如文献分析、学生口语报告法和领域专家判断等确定测验的Q矩阵,然而,这些方法都或多或少具有一定的主观性。如,对于分数减法的属性界定至今仍存在很多的争议性(de la Torre, 2008; DeCarlo, 2011, 2012)。因此,研究者提出直接从学生作答数据中估计测验Q矩阵。DeCarlo(2012)基于DINA模型(Junker, & Sijtsma, 2001),提出可以使用贝叶斯方法直接估计Q矩阵中不确定的元素。贝叶斯方法在一定程度上克服了主观性,但需要事先知道Q矩阵中哪些元素或项目是不确定的。Liu,Xu和Ying(2012)尝试通过最小化S统计量直接从作答数据估计出Q矩阵,并证明了估计的Q矩阵收敛于真实Q矩阵。但此方法在计算题目数和属性个数时,计算量巨大且耗时。喻晓锋等人(2015)直接从模型—数据拟合的角度,构建并使用似然比D2统计量,在搜索算法的基础上,通过一定数量的基础题(即属性考核模式已知的项目),使用LROE(Likelihood Ratio Online Estimation)算法,来定义题目考核模式,进而估计Q矩阵。模拟研究显示,该方法可以较好地用于在线项目估计,在执行效率上也较Liu,Xu和Ying(2012, 2013)的S统计量更高。根据模型—数据拟合的思路,汪大勋,高旭亮,蔡艳,涂冬波(2018)和汪大勋,高旭亮, 韩雨婷,涂冬波(2018)分别通过重现建构属性一致性指标(hierarchy consistency index; HCI)和RSS(residual sum of squares)指標,提出了两种非参数的Q矩阵估计方法,即ICC-IR(ICC based on ideal response)法和基于海明距离的 Q 矩阵估计方法。非参数估计方法操作简单,但不能获取题目的相关参数,不能进行项目质量的评估与拟合检验等。且与喻晓锋等(2015)方法相似,ICC-IR法和基于海明距离的 Q 矩阵估计方法通过搜索算法使得项目对应的指标或统计量最大/最小,实现对Q矩阵的估计,相比Liu等(2012,2013)的S统计量方法更简单明了,便于操作,但由于没有明确的拟合范围,在修正阶段需要对Q矩阵中的题目进行逐个修正,直至收敛。如果初步估计的Q矩阵正确题目较多,就会浪费时间,如果正确的题目较少,错误的题目可能会影响统计量的准确性,进而把正确的题目重新估计错误。
一个好的用于Q矩阵估计的拟合统计量,应该简单高效且有确定的拟合范围。 von Davier(2005)提出了一个可以用于认知诊断的项目拟合统计量近似误差均方根(Root Mean Square Error of Approximation, RMSEA)。Kunina-Habenicht, Rupp和Wilhelm(2009,2012)通过模拟和实证研究,将该统计量作为评估认知诊断测验中项目质量拟合好坏的指标,并给出了拟合范围:RMSEA小于0.05为拟合很好;介于0.05~0.1为中度拟合;大于0.1为不拟合。Kang, Yang和Zeng (2019)进一步将该统计量应用于Q矩阵的修正中,并从数理上证明了该统计量的合理性,模拟研究表明,该统计量可以找出Q矩阵的不拟合项目并进行修正。然而, Kunina-Habenicht等(2009, 2012)和Kang等(2019)使用RMSEA探测不拟合项目或进行Q矩阵修正,但并没有进一步使用RMSEA对Q矩阵进行估计。借鉴喻晓锋等(2015)LROE算法的思路,使用项目拟合统计量RMSEA对Q矩阵进行估计,在修正阶段就可以利用其拟合范围找到不拟合项目,然后仅对不拟合项目中的项目进行修正,应该能在一定程度上节省搜索时间,提高修正效率。为此,本文拟提出一种基于RMSEA的Q矩阵估计方法,并通过模拟研究验证其估计效果。研究包括:(1)基于RMSEA的Q矩阵修正算法; (2)算法的有效性及效率; (3)讨论与结论。
2 基于RMSEA的Q矩阵修正算法
2.1 DINA模型
本研究使用DINA模型来考察该统计量作为Q矩阵估计的拟合统计量,DINA模型易于解释且简洁,具有扩展到更复杂认知诊断模型的潜力(de la Torre,2009;Park & Lee,2014)。并且DINA模型常被用于Q矩阵估计和修正方法的研究中(涂冬波,蔡艳,戴海崎,2012; 汪大勋,高旭亮等,2018;喻晓锋等,2015; DeCarlo, 2012; de la Torre,2008)。
2.2 最小统计量算法
Chiu(2013)基于非参数分类方法,提出通过计算项目的RSS值来为可能存在错误的项目进行重新定义。对于项目j,如果属性考察个数k已知,那么该项目的可能属性向量就可以知道。比如,基于DINA模型,不考虑属性之间的层级关系,对于任何项目,其可能的属性向量均为2k-1种。基于非参数方法,计算项目j在不同属性向量下的RSS值,找到使得RSS值最小所对应的那个属性向量,并把其作为项目j新的属性向量。类似的,喻晓锋等(2015)、汪大勋等(2018)在一定数量的基础题上,采用“增量”的方式,即每次只考虑一个项目,通过计算项目的似然比统计量D2,利用LROE算法,寻找每个项目j在不同属性向量下的最小D2对应的属性向量,对项目进行逐个估计,进而估计Q矩阵。为便于表述,本文将这种通过寻找统计量最小值对应的项目属性向量来对项目进行重新定义的方法,称为最小统计量算法。
最小统计量算法通过每次估计一个项目,来对Q矩阵进行定义或修正,一般包括两个阶段:估计阶段和校正阶段。在估计阶段,利用不同的估计方法,如非参数分类方法或EM算法,估计获得被试的属性掌握模式或项目参数,计算不同属性向量对应的项目统计量值,并把项目重新定义为统计量值最小时对应的属性向量。在校正阶段,对所有项目逐个进行估计,直至达到某个收敛标准(汪大勋等,2018;喻晓锋等,2015)。
2.3 基于RMSEA的最小统计量算法
本文借鉴前人研究的思路,介绍基于最小RMSEA的Q矩阵修正算法,因RMSEA为基于卡方的统计量,为方便介绍,将基于RMSEA的算法命名为CSE(Chi Square Estimation)算法。假设已有少量属性向量正确的项目,称为基础题,记为Qbase;属性未知的项目称为新题,记为Qnew。CSE算法的具体步骤如下:
第一步,估计阶段:
(1)从需要定义的新题Qnew中选取一个,为qnew,将其加到Qbase中;同时把受测者在qnew上的作答数据也加到Qbase的作答数据中。
(2)为qnew选择可能的属性向量,根据选择的属性向量组成的新Q矩阵和作答数据(Qbase和qnew组合而成),使用EM算法(de la Torre,2009)进行参数估计。
(3)计算每种可能的属性向量下,qnew的项目拟合统计量RMSEAqj,选择项目拟合统计量RMSEAqj最小时,qnew对应的属性向量为其题目属性向量,把该题纳入Qbase,记作Qbase2
(4)把qnew从Qnew中忽略,即Qnew2=Qnew\(qnew)。
(5)把Qbase2和Qnew2分别赋值给Qbase和Qnew,重复1~4,直至所有新题估计完成,得到估计后的Q矩阵,记为Q0。
第二步,校正阶段:
(1)以所有作答数据(即Qnew和Qbase上的作答数据)和Q0矩阵进行参数估计,计算每题的项目拟合统计量RMSEAj。
(2)找出其中项目拟合统计量RMSEAj大于0.05的项目。
(3)计算每种项目属性向量下,项目j的项目拟合统计量RMSEAj,并把项目拟合统计量RMSEAj最小时对应的项目属性向量更新为项目j的属性向量。直至所有项目拟合统计量RMSEAj大于0.05的项目都进行了校正。
(4)算法结束,此时所得Q矩阵作为最终估计值。
已有的研究使用最小统计量算法对Q矩阵的项目逐个进行估计,实现对属性向量未知项目的定义。但是,初步估计得到Q矩阵仍可能存在错误,需反复逐个项目校正直至达到某个收敛标准。这种没有针对性的校正耗费时间,且可能出现不收敛的情况。CSE算法使用RMSEA的拟合范围,只对拟合不好的项目进行重新估计,可以大大缩减算法执行时间,提高修正效率。
3 模拟研究:CSE算法的有效性及效率3.1 研究目的
为了研究最小RMSEA算法对Q矩阵估计的有效性和效率,即使用一定数量的基础题,逐个加入新题,利用CSE算法对新题进行估计。从属性個数、基础题个数和被试人数等3个方面考察CSE算法的稳健性。
3.2 研究方法
3.2.1 研究设计
在被试的属性掌握模式为均匀分布的情况下,研究为包含3种属性个数(K=3,4,5),4种被试人数(N=400,500,800,1000),5种基础题个数(J=8,9,10,11,12)的3×4×5的交叉设计,共60种条件。包含20个题目的Q矩阵真值(喻晓锋等,2015; Li ,Xu & Ying, 2012),见图1。其考察的属性个数递增,分别为3、4、5,记为Q1、Q2、Q3。
3.2.2 数据模拟
DINA模型下,当属性考察个数为K时,被试属性掌握模式为2k种;将被试按均匀分布分配到各属性掌握模式中,使每种属性掌握模式上的人数大致相等。然后使用公式1,分别得到被试在Q1、Q2、Q3上的理想反应模式(Ideal Response Pattern, IRP);生成题目参数s和g,在区间[ 0.05,0.25 ]随机产生且服从均匀分布(喻晓锋等,2015)。根据IRP使用公式2,计算被试在Q1、Q2、Q3上的正确作答概率,并将其与均匀分布U(0,1)的随机数比较,当正确作答概率大于随机数,则被试作答正确,否则作答错误。
每种条件模拟100批数据,从中随机抽取不同个数的基础题及其对应的属性向量作为初始Q矩阵,这样每种基础题个数下都有100个初始Q矩阵。
3.2.3 参数估计与数据分析
以初始Q矩阵和对应的被试作答数据作为估计算法的出发点,使用CSE算法的第一步,逐个将新题加入到基础题中进行估计,直至所有新题估计完成。使用CSE算法第二步进行校正,确定最终Q矩阵。
3.2.4 评价指标
对于不同基础题个数,计算CSE算法在100个初始Q矩阵下的估计成功率(估计得到的Q矩阵与原始Q矩阵的相同率),以此作为算法的评价指标(汪大勋等,2018;喻晓锋等,2015; Liu,Xu & Ying,2012)。3.3 研究结果
3.3.1 CSE算法具有较高的估计成功率
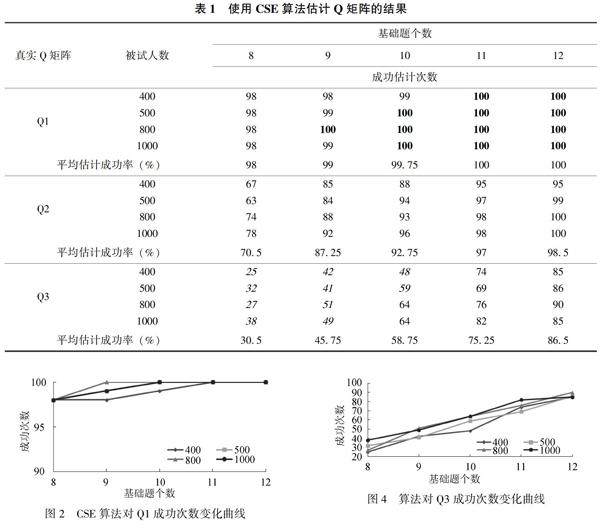
表1是各条件下CSE算法的估计结果。从表1可以看出,CSE算法的成功率分布范围为25%~100%,除了Q3时8,9,10个基础题下的成功率较低外,其他各条件下的成功率均较高。纵观60个条件下的成功率(每条件下均为重复100次的均值),可以发现:在14个条件下,其成功率为100%(见加黑的数字),成功率在90%~99%的有18个条件,在80%~90%的有8个条件。由此,60种实验条件下,成功率在80%以上的有40个。此外,成功率在60%以下的有10个条件,为属性个数较多基础题又较少的各个条件(见表1斜体数字)。
3.3.2 成功率受样本容量的影响相对较小
结合表1和图2、图3、图4可以看出,相对属性数目(Q矩阵)和基础题个数,CSE算法估计成功率受样本容量影响甚微。在Q1条件下,5种基础题个数下的成功率在样本容量上的变量最大只有2%(基础题9时, 样本容量400~800变化时的98%~100%), 多数条件下成功率基本不变; 在Q2和Q3条件下, 成功率随样本容量的变化稍微大点,但一般情况下也只变化5、6个百分点,最大也只变化了15个百分点,为Q2条件下8基础题时,样本容量500~1000时的63%~78%。因此,在属性数目较少时,样本容量基本不影响CSE算法的估计成功率,但随着属性数目的增多,样本容量也不宜太小。
3.3.3 成功率受属性数目和基础题个数影响显著 从表1中的平均估计成功率,结合图2、图3、图4纵坐标的截距点和变化趋势明显地看出, 相对于样本容量,CSE算法成功率受属性数目和基础题个数影响显著。从3个图中可以看出,各样本容量的变化趋势线挨得很近,表明成功率受样本容量影响甚微。然而,各图中纵坐标的起点和终点差异很大,表明成功率受属性数目和基础题个数影响明显。具体而言:当基础题个数从8个增加到12个时,成功率的变化为:Q1时, 成功率从98%增加到100%; Q2时, 成功率从70.5%增加逐步递增到98.5%,起点较Q1时低,但变化幅度较Q1时大,增加了28个百分点;Q3时,起点再次降低,幅度再次提升,从30.5%增加到86.5%,上升了56个百分点。进一步对Q1、Q2、Q3不同基础题个数的估计成功次数进行Kurskal-Wallis H检验,结果显示不同个数的基础题估计成功率有显著差异,分别为χ22=14.85, df=4,p<0.01;χ22=16.72, df=4,p<0.01;χ22=17.91, df=4,p<0.001。由此,可以得出:CSE算法估计成功率随着属性数目的增加而减低,随着基础题个数的增加而升高,但受样本容量影响相对较小。在Q矩阵估计中,基础题个数非常重要,当属性数目没办法改变时,提高成功率的重要途径则是增加基础题个数。
3.3.4 CSE算法的执行时间少,具有较高的效率 表2列出了各条件下算法完成一次估计和校正的平均用时。在60个条件下,平均用时的波动范围为约9s(N=1000, J=12, K=3)~15min(N=500,J=8,K=5)。纵观表2的所有数据,可以发现:执行时间受属性数目影响较大,而与基础题个数和样本容量关系不大。表2最右侧列出了各条件下的平均用时。Q1时,所需时间为10.07~10.70秒;Q2时,所需时间为139.10~180.11秒;Q3时,所需时间为635.60~682.50秒。可见,在每个Q矩阵内部,执行时间因样本容量和基础题个数影响甚小,但在每个Q矩阵之间,每增加一个属性,所需时间从10秒左右变化到100多秒直至5个属性时的600多秒。
4 实证研究:CSE算法在实证数据中的应用 为进一步探讨CSE算法在实际应用中的效果,本研究使用该方法对K. K. Tatsuoka (1990)的分数减法数据进行分析,数据包含了536名学生在15个测验项目上的作答,測验考察了5个属性,测验Q矩阵改编自Missevy(1996)。该数据在之前的Q矩阵的估计和修正研究中均被使用(汪大勋等,2018;DeCarlo, 2012; de la Torre, 2008)。根据原始作答数据和Q矩阵,使用DINA模型计算出各项目的鉴别度指数(item discrimination index, IDI; Lee, de la Torre & Park,2012)。将数据按IDI从高到低排列,分别选取前6、7、8、9、10题作为基础题,对剩余项目逐个进行估计。分析重新估计后的Q矩阵与原始Q矩阵的一致性程度,其中Q矩阵共有15×5=75个元素,计算相同元素的比例(括号内为相同元素个数),结果如下表。从表3可以看出,使用不同基础题个数,估计得到的Q矩阵与原始Q矩阵一致性程度差异不大,说明不同基础题个数下Q矩阵的估计结果趋于稳定。
为比较估计的Q矩阵与原始Q矩阵的合理性,这里分别计算根据不同Q矩阵其模型拟合指标(即负2倍的对数似然、AIC和BIC指标)。结果见表4。从表4可以看出,重新估计的Q矩阵在拟合指标上优于原始Q矩阵,且随着基础题个数的增加,呈现逐渐优化的趋势。在基础题为10个时, 各拟合指标相比于9个时略变差,这可能是因为基础题为10个时,基础题包含鉴别指数前10的项目,第10个项目鉴别指标较小,作为基础题有一定偏差。总体而言,估计Q矩阵在基础题9个时达到最优,且优于原始Q矩阵拟合水平。
5 讨论
Q矩阵界定是认知诊断研究中的一个重要问题,尤其是在认知诊断计算机自适应测验中,常常需要对题库的项目进行在线标定。为获得有效、客观的Q矩阵,本文从项目拟合的角度,提出一种基于项目拟合统计量RMSEA的Q矩阵项目估计思路,并通过模拟和实证研究考察了方法的有效性和稳定性。
5.1 RMSEA可以作为题目属性向量估计的有效指标 使用CSE算法基于一定数量的基础题对新题逐个进行估计,并把0.05作为拟合临界值,在校正阶段只对大于拟合值的项目进行重新估计,耗时较短,效率较高。为了说明CSE算法的有效性和效率,加入与同样基于参数的Q矩阵估计的LROE算法的比较。
从表5可以看出,在属性考察个数为3个或4个时CSE算法估计成功率比LROE算法高,这可能是因为当属性个数较少时,基于相同数目的基础题,RMSEA能准确地找到项目属性向量,在校正阶段可以有效的识别并校正错误项目而不是对所有项目进行重新估计。当属性考察个数为5个时,CSE算法估计成功率总体较LROE算法略低,这可能是因为属性个数为5个时,基础题个数较少,估计得到的Q矩阵包含的错误较多,当使用拟合临界值作为修正临界值,对Q矩阵中错误的项目不能有效的识别并修正。不过,两者所呈现的趋势仍然是一致的,即随着基础题个数的增加,算法的表现越来越好。因此,当属性个数较多时,可以适当增加基础题以达到较为理想的效果。此外,从表6可以看出,CSE算法在各条件下所花费时间明显比LROE算法少,这表明CSE算法效率较高。
关于临界值的选取,Kunina-Habenicht等(2012)指出I类错误率相同的情况下,对于不同条件(样本大小和属性考察个数)没有单一的截断值,研究者或应用者可以根据特定的条件进行模拟,获取该条件下更精确的临界值。不过可以肯定的是,当Q矩阵错误较少时,选择较为宽松的临界值可以节省时间,且可达到较好的修正效果(Kang et al., 2019)。这也说明选取一个合适的截断值,不仅可以有效的识别和修正Q矩阵中的错误,也可以减少Q矩阵估计时修正阶段所花费的时间。未来研究可以进一步探讨,不同条件下,临界值的选取对Q矩阵估计的影响。此外,该方法对被试人数的要求不高,但对于基础题(即属性向量界定正确的题目)个数有一定要求。
5.2 CSE算法用于實证数据分析效果较好
对于分数减法的属性界定至今仍存在很多争议(DeCarlo,2011,2012; de la Torre, 2008),本研究通过将CSE算法应用于分数减法数据的分析,发现使用不同数量的基础题,能在一定程度上提高数据—模型的拟合水平;且随着基础题个数的增加,该方法的表现逐渐变好,这与模拟研究发现的结果一致。在基础题个数为9个时,估计Q矩阵拟合情况整体最好, 与汪大勋, 高旭亮, 韩雨婷等(2018)所得结果较为一致。由此,该方法在用于实证数据的分析时也可以取得较好的效果。
此外,CSE算法是一种直接从模型—数据拟合角度对Q矩阵进行估计的方法,对被试数量要求不高,并且不同认知诊断模型RMSEA的计算在R语言直接调用即可,具有较强的适用性,可以满足多种研究或实践的需要。
6 结论
本研究通过模拟实验和实证数据分析,探讨了将RMSEA用于Q矩阵估计的方法的可行性、有效性及效率问题,得到以下结论:(1)基于RMSEA的CSE算法可以有效地估计新题的属性向量,且耗时较少;(2)对Q矩阵估计的成功率受属性数目和基础题个数影响甚大,尤其是当属性数目较多时,要求有较多的基础题个数;(3)该统计量对被试数量要求不高,即使被试人数为400人,只要基础题个数足够多,估计效果依然较好,可适于中等规模的测评中;(4)该方法应用于实证数据的分析,可以一定程度的优化已有的分析结果,提高模型—数据的拟合性。
参考文献
涂冬波, 蔡艳, 戴海崎(2012). 基于DINA模型的Q矩阵修正方法. 心理学报, 44(4), 558-568.
汪大勋, 高旭亮, 韩雨婷, 涂冬波(2018). 一种简单有效的Q矩阵估计方法开发:基于非参数化方法视角. 心理科学, 41(1), 180-188.
汪大勋, 高旭亮, 蔡艳, 涂冬波(2018). 一种非参数化的Q矩阵估计方法:ICC-IR方法开发. 心理科学, 41(2), 466-474.
喻晓锋, 罗照盛, 高椿雷, 李喻骏, 王睿, 王钰彤(2015). 使用似然比D2统计量的题目属性定义方法. 心理学报, 47(3), 417-426.
Chiu, C. Y. (2013). Statistical Refinement of the Q-matrix in Cognitive Diagnosis. Applied Psychological Measurement, 37(8), 598-618.
DeCarlo, L. T. (2011). On the analysis of fraction subtraction data: The DINA model, classification, latent class sizes, and the Q-matrix. Applied Psychological Measurement, 35(1), 8-26.
DeCarlo, L. T. (2012). Recognizing uncertainty in the Q-matrix via a Bayesian extension of the DINA model. Applied Psychological Measurement, 36(6), 447-468.
de la Torre, J. (2008). An empirically based method of Q-matrix validation for the DINA model: Development and applications. Journal of Educational Measurement, 45(4), 343-362.
de la Torre, J. (2009). DINA model and parameter estimation: A didactic. Journal of Educational and Behavioral Statistics, 34(1), 115-130.
de la Torre, J., & Chiu, C. -Y. (2010). A General Method of Empirical QMatrix Validation Osing the GDINA Model Discrimination Index. Paper Presented at the Annual Meeting of the National Council on Measurement in Education, Denver.
Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258-272.
Kang, C., Yang, Y., & Zeng, P. (2019). Q-Matrix Refinement Based on Item Fit Statistic RMSEA. Applied Psychological Measurement, 43(7), 527-542.
Kunina-Habenicht, O., Rupp, A. A., & Wilhelm, O. (2009). A practical illustration of multidimensional diagnostic skills profiling: Comparing results from confirmatory factor analysis and diagnostic classification models. Studies in Educational Evaluation, 35(2-3), 64-70.
Kunina-Habenicht, O., Rupp, A. A., & Wilhelm, O. (2012). The impact of model misspecification on parameter estimation and item-fit assessment in log-linear diagnostic classification models. Journal of Educational Measurement, 49(1), 59-81.
Lee, Y. S., de la Torre, J., & Park, Y. S. (2012). Relationships between cognitive diagnosis, CTT, and IRT indices: An empirical investigation. Asia Pacific Education Review, 13(2), 333-345.
Liu, J., Xu, G., & Ying, Z. (2012). Data-driven learning of Q-matrix. Applied psychological measurement, 36(7), 548-564.
Liu, J., Xu, G., & Ying, Z. (2013). Theory of the self-learning Q-matrix. Bernoulli, 19(5A), 1790-1817.
Mislevy, R. J. (1996). Test theory reconceived. Journal of Educational Measurement, 33(4), 379-416.
Park, Y. S., & Lee, Y. S. (2014). An extension of the DIAN model using covariates: examining factors affecting response probability and latent classification. Applied Psychological Measurement, 38(5), 376-390.
Rupp, A. A., & Templin, J. (2008). The effects of Q-matrix misspecification on parameter estimates and classification accuracy in the DINA model. Educational and Psychological Measurement, 68(1), 78-96.
Tatsuoka, K. K. (1990). Toward an integration of item-response theory and cognitive error diagnosis. Diagnostic monitoring of skill and knowledge acquisition, 453-488.
von Davier, M. (2005). A general diagnostic model applied to language testing data. ETS Research Report Series, 2005(2), 1-35.
Abstract
Usually, cognitive diagnostic assessment (CDA) is based on a test and the corresponding cognitive diagnostic model to construct a diagnostic analysis. Many approaches need a Qmatrix which reflects how attributes are measured in each item when applying the cognitive diagnosis model into an assessment. Qmatrix plays an important role in CDA. Qmatrix can be defined by experts in related fields, and also can be estimated according to students response data. Based on the existing Qmatrix refinement methods, a Qmatrix estimation method using an item fitting statistics RMSEA is proposed. The effectiveness and efficiency of the method are verified by a simulation study. And a real data analysis is also included. The results show that: (1) the CSE algorithm based on RMSEA can effectively estimate the attribute vectors of new items, and it takes less time; (2) the success recovery rate of Qmatrix estimation is greatly affected by the number of attributes and the number of basic items, especially when the number of attributes is large, it requires more basic items to estimate the attribute vectors of new items; (3) The sample size has little effect on the performance of CSE approach and a big sample size is not necessary to implement the Qmatrix modification method. Even if the number of subjects is 400, as long as the number of basic items is enough, it can have a high recovery ratio; (4) The application of this method to the analysis of empirical data can optimize the existing analysis results to a certain extent and improve the fitting of model-data.
Key words: cognitive diagnosis; Qmatrix estimation; item fit statistic; DINA model

