基于混合效应的湖南栎类与杉木单木断面积生长模型研究*

钟栋明 黄华蓉 李临兵 徐誉远

（广东省岭南综合勘察设计院，广东 广州 510663）

把握林木生长发育规律，对于指导树木的生产经营与利用具有重要作用，其生长规律既有时间积累下来的定性经验，又可用生长模型等方法来定量测定。目前，林分的生长模型可分为全林分模型、径阶分布模型和单木生长模型[1]，前两种是反映林分或径阶的平均变化状态，着重于总体趋势的变化。而单木生长模型[2-3]能直观反映年龄、立地和竞争等因子对单一树木的生长影响，预估精度高的单木模型能有效地预估树木的生长动态，为林分质量的精准提升提供依据，因此单木生长模型一直是林业科研工作者的研究重点。

在传统建模中，往往只考虑单一因素对树木生长的影响，如胸径对树高[4]、胸径对冠幅[5]的影响，这样的单木预估模型拟合精度一般，对树木的生长反映不够灵敏。树木的生长受自身遗传因素的影响较大，但林木竞争、立地条件、气候等因子的影响也不可忽略。因此，一些学者尝试引入混合效应来提高生长模型预估精度，同时综合反映不同因子对树木生长的影响。如符利勇等[6]考虑林场与样地效应构建的蒙古栎(Quercus mongolica)单木断面积模型拟合精度明显优于传统模型；李春明等[7]基于样地效应构建落叶松(Larix gmelinii)林分断面积模型，其拟合精度明显高于传统的非线性回归方法。目前，混合效应模型已应用于杉木、落叶松、马尾松(Pinus massoniana)等速生针叶树种，而关于栎类次生林的研究较少。

栎类是我国常绿阔叶林的主要建群树种之一，是我国分布最广、面积最大的重要森林资源。但目前很多栎类林都是经砍伐后萌生的次生林，普遍存在林分过密、萌生、细长杆材等质量低下问题[8]。湖南的栎类资源丰富，总面积占全省阔叶林面积的13%，栎类树种达到6 属77 种，主要树种为青冈栎(Cyclobalanopsis glauca)、石栎(Lithocarpus glaber)、甜 槠(Castanopsis eyrei) 等，其中栎类的主要混交类型包括有栎类-杉木、栎类-马尾松、栎类-阔叶树混交林，栎类-杉木混交林类型广泛分布于全省岳阳、怀化、郴州等14 个地级市和自治州，总面积占据栎类资源的18%以上，是湖南省一种主要的森林类型[9]。考虑到混交树种的复杂性以及栎类杉木混交林的重要性，本研究以栎类和杉木占主要优势的栎类杉木混交次生林为主要研究对象，基于样地随机效应分别构建栎类与杉木的断面积混合效应模型，为进一步把握栎类与杉木的生长规律，提高栎类资源的林分质量提供参考。

1 研究区概况

湖南省位于长江中下流，洞庭湖以南，地理坐 标 为108o47′～114o15′E，24o38′～30o08′N。境 内海拔分布范围24～2 122 m，地形地貌复杂，包括有丘陵、平原、山地等，全年春夏湿润多雨，秋冬少雨干旱，为典型的大陆性亚热带季风湿润气候，年平均气温在15～18oC，年均降雨量1 200～1 700 mm。境内的土壤以红壤、黄壤为主，少量分布有石灰土、潮土等。湖南省位于中亚热带常绿阔叶林地带，境内植被资源丰富，主要分布树种有杉木、马尾松、枫香(Liquidambar formosana)、樟树(Cinnamomum camphora)、青冈栎等。

2 数据来源与方法

2.1 数据来源

研究数据来源于湖南省第八次森林资源连续清查数据库，从中筛选以栎类和杉木为主要组成树种的样地共31 块，其中岳阳市7 块、怀化市6块、永州市6 块、郴州市5 块、益阳市4 块、湘西自治州3 块。为确保研究样本的一致性与代表性，样地筛选时按照以下标准进行：样地郁闭度在0.7 以上；每公顷株树在1 000 株以上；样地内栎类与杉木的总株数占样地总数的70%以上；样地受人为干扰程度较少。研究样地为25.8 m×25.8 m 的正方形，主要调查计算因子包括每木胸径、年龄、断面积和树种等林木因子，海拔、坡度、坡向、坡位、土壤、郁闭度等林地因子。林木年龄由龙时胜等[10]方法计算而来，其中，在6 块样地中分别选取20 株树木，利用生长锥钻取树木木芯样本，通过计算年轮的方法确定了树木的实际年龄，结果表明实测年龄与该方法的误差控制在20%以内。

经筛选后确定的样本数为栎类1 646 株，杉木1 154 株，样地、栎类与杉木的基本概况见表1。为确保所建立的模型科学合理，研究选取总样本的2/3（1 867 株）作为建模数据，1/3（933 株）作为验证数据。

表1 样地与样木基本概况Table 1 The basic situation of sample and wood

2.2 研究方法

研究拟构建以样地为随机效应的栎类、杉木断面积生长混合效应模型，其中断面积为因变量，林木年龄为自变量。混合效应模型的具体构建与评价步骤如下。

2.2.1 基础模型的筛选 相关研究表明，理论生长模型在描述林木的生长过程时往往优于经验模型，为进一步验证该理论，研究考虑选取3 个经验模型（线性、指数和二次函数）和4 个生长模型（Schumacher、Richards、Gompertz、Logistic）作为模拟断面积生长的基础模型，基础模型的表达式如表2。

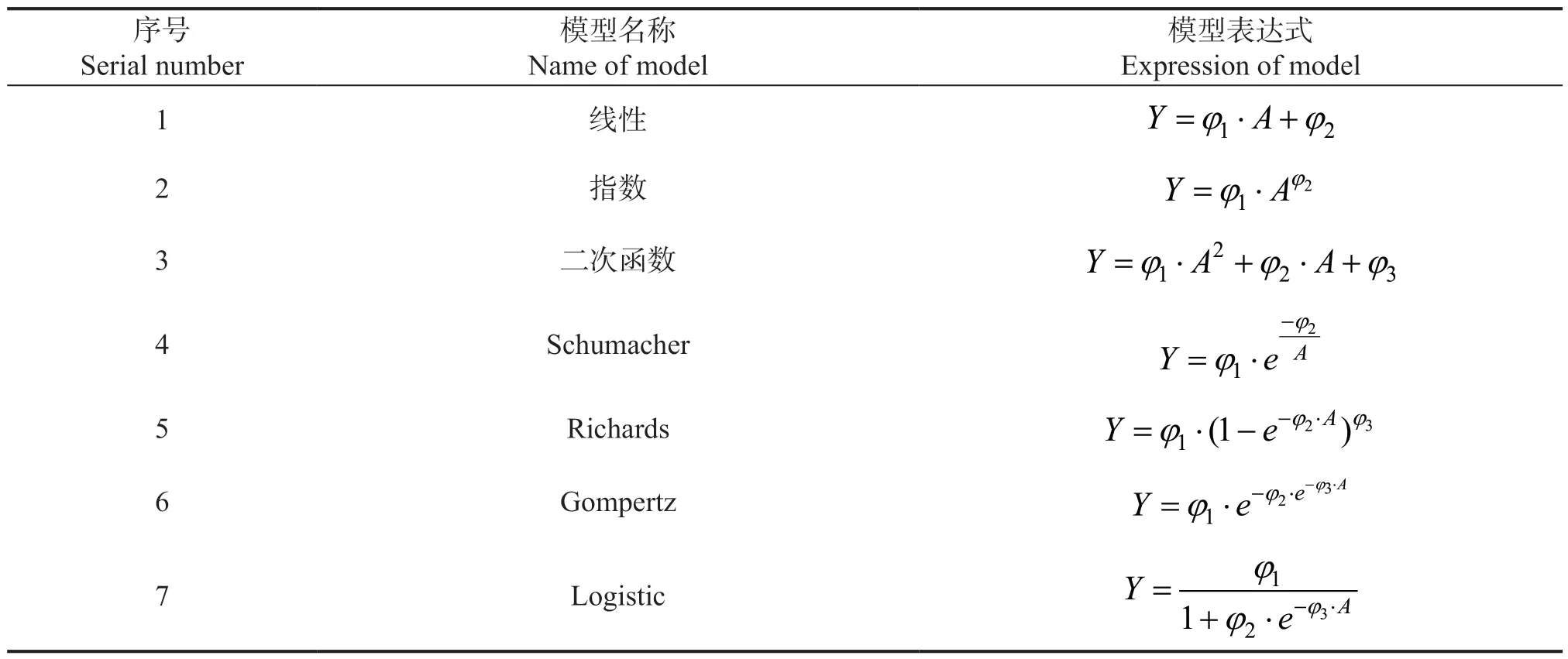
表2 基础模型表达式Table 2 The expression of base model

2.2.2 混合效应模型的构建 混合效应模型是依据回归函数依赖于固定效应参数和随机效应参数的线性或非线性关系而建立的[11]。考虑到不同样地之间的树木生长可能存在差异，本研究以林木年龄为固定效应，样地为随机效应，拟构建栎类与杉木的单木生长混合效应模型，其表达式为：

式中，Yij为第i个样地第j株林木的断面积；Aij为第i个样地第j株林木的年龄；m为样地个数；ni为第i个样地的林木株数；f是关于参数向量φij的函数；β为p×1 维固定效应参数；ui为q1×1 维的样地随机效应参数，假定服从期望为0，方差为ψ的正态分布；φij为形式参数，它与β，ui呈线性函数关系；aij、bij分别为β、ui的设计矩阵；εij为随机误差项，假定ui、εij之间相互独立。

混合效应模型的构建关键在于形式参数的构建，形式参数如何构造争议较大，目前还没有一个统一的标准。本研究选用一种常用的方法，即在保证模型收敛的情况下，考虑基础模型中所有形式参数都为混合参数，利用评价指标-赤池信息准则（Akaike Information Criterion，AIC）和贝叶斯信息准则（Bayesian Information Criterion，BIC）对所有形式参数组合类型进行比较。AIC 与BIC两者的原理有所差异，AIC 是从预测角度选择一个好的模型用来预测，BIC 是从拟合角度选择一个对现有数据拟合最好的模型，但两者都能有效避免模型精度过高而造成模型过度复杂的现象，模型评价过程中AIC 和BIC 越小越好[12]，两个评价指标的表达式分别为：

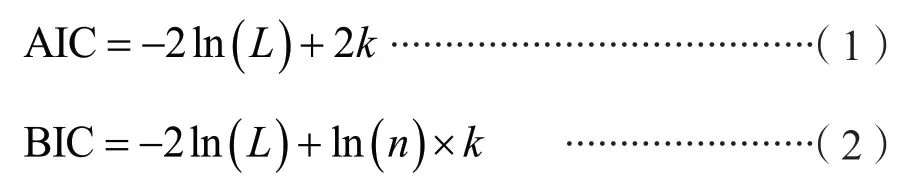
式中，k为参数个数；n为样本数；L为模型的似然函数。

2.2.3 模型评价与检验 模型的评价指标包括决定系数（R2）、相对均方根误差(RRMSE)、残差平方和(SSE)共3 个指标，R2越大，RRMSE 和SSE越小，模型拟合效果越佳。根据建模数据求出7个模型的参数，依据3 个评价指标进行对比，就可筛选出最优的基础模型，然后利用检验数据评价基础模型与混合效应模型的拟合效果。其中，3个评价指标的表达式为：

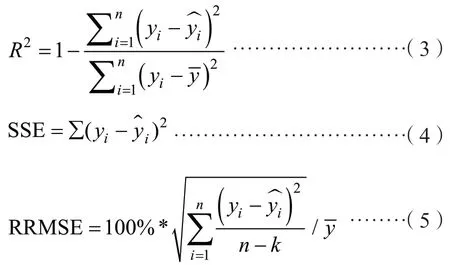
式中，n为样本数；y为测量值；为预估值；为测量值的平均值；k为参数个数。

3 结果与分析

3.1 基础模型拟合结果

利用7 个基础模型分别拟合栎类与杉木的断面积生长模型，结果见表3。除线性模型外，栎类单木断面积生长模型的决定系数均在0.711 以上，非线性模型的拟合效果较好，其中Gompertz模型的拟合效果最佳（R2=0.845，SSE=0.037，RRMSE=5.64%），可作为栎类单木断面积的最优基础模型；除线性模型外，杉木单木断面积生长模型的决定系数均在0.733 以上，非线性模型的拟合效果较好，其中Logistic 模型的拟合效果最佳（R2=0.746，SSE=0.032，RRMSE=4.79%），可作为杉木单木断面积的最优基础模型。

表3 栎类与杉木断面积生长模型拟合结果Table 3 The fitting results of basal area model of Quercus sp. and Cunninghamia lanceolata

3.2 混合效应模型拟合结果

基于样地水平，构建栎类的断面积混合效应生长模型，针对不同形式参数的组合，利用AIC、BIC 两个统计指标对模型的拟合优度进行比较，AIC 与BIC 值越小，模型拟合效果越好。由表4的结果可知，栎类的断面积生长混合效应模型随机参数位于φ1时，模型的AIC、BIC 指标最小。其中，栎类的混合效应生长模型AIC、BIC 均明显小于基础模型的AIC、BIC，说明基于样地水平的栎类混合效应模型拟合效果优于基础模型。

表4 栎类的混合效应模型拟合结果Table 4 The fitting results of mixed effect model of Quercus sp.

基于样地水平，构建杉木的断面积混合效应生长模型。由表5 可知，杉木的断面积生长混合效应模型随机参数位于φ1时，模型的AIC、BIC 指标最小。其中，杉木的混合效应生长模型AIC、BIC均明显小于基础模型的AIC、BIC，说明基于样地水平的杉木混合效应模型拟合效果优于基础模型。

表5 杉木的混合效应模型拟合结果Table 5 The fitting results of mixed effect model of Cunninghamia lanceolata

3.3 栎类与杉木的生长规律

对比分析栎类与杉木的断面积生长规律，结果如图1。栎类的断面积生长过程较为缓慢，且随着年龄的增大呈增加的趋势，说明栎类的成熟年龄在50 年以后；杉木的断面积生长速率明显高于栎类，且在30 年左右生长速率逐步放缓，之后生长趋于稳定。

图1 栎类与杉木的生长规律Fig.1 The growth law of Quercus sp. and Cunninghamia lanceolata

3.4 模型检验与评价

基于检验样本对栎类与杉木的最优基础模型与混合效应模型拟合效果进行检验。由表6 可知，栎类断面积生长混合效应模型的决定系数R2比基础模型增加0.053，残差平方和SSE 与相对均方根误差RRMSE 均有所降低，检验数据的结果进一步表明栎类的混合效应模型拟合效果优于基础模型；杉木断面积生长混合效应模型的决定系数R2比基础模型增加0.035，残差平方和SSE 与相对均方根误差RRMSE 均有所降低，检验数据的结果进一步表明杉木的混合效应模型拟合效果优于基础模型。

表6 基础模型与混合效应模型的拟合效果对比Table 6 Comparison of the fitting results between basic and mixed effect model

4 结论与讨论

莫辉等[13]在构建木荷的直径、树高与材积生长模型时发现，与经验模型相比，理论生长模型在模型拟合精度及生物学解释上均具有一定优势；吕勇[14]在研究杉木与马尾松树高生长模型时也具有同样的结论。本研究在构建栎类与杉木的断面积生长模型时发现，栎类的最优基础模型为Gompertz 理论生长模型，杉木的最优基础模型为Logistic 模型，理论生长模型的拟合精度总体高于经验模型，说明理论生长模型在拟合林木的生长过程时能比较准确的反映出树木随年龄的累积变化规律，且在生物学解释具有一定的优势。

树木的生长变化是林木遗传特性、林木竞争以及立地条件综合影响的结果，单一方面的指标无法很全面的反映树木的生长过程。混合效应模型在考虑林木的平均变化趋势时，还能体现出个体或立地对林木生长的影响，在构建树木的生长模型方面具有优势。部分研究表明，模型中加入样地随机效应能有效的提高模型的拟合精度，如李春明[15]在构建杉木蓄积联立方程的基础上引入样地混合效应，结果显示，混合效应模型的拟合效果明显优于基础模型；刘洵等[16]在栎林生长收获模型中加入样地层次的混合效应后，模型精度得到很大改善。样地随机效应是对立地因子差异性的反映，不同样地的海拔、坡度、坡向、土壤等往往存在差异，而这种差异性就会导致树木的生长规律表现不一。本研究在栎类与杉木的断面积生长模型中加入样地随机效应后，模型拟合精度得到提高，说明栎类与杉木的生长不仅受固定效应年龄的影响，在不同样地之间也会表现出差异性。

异龄混交林中单株树木年龄的测定一直是林业工作中的重点与难点，目前还没有一种准确性高、操作成本低廉的有效测定方法。龙时胜等[10]采用林木多期直径数据估计异龄林的年龄，能确保单木的平均绝对百分误差控制在14.8%以内，对于树木年龄的估计具有一定的参考价值。本研究参考此方法，利用生长锥选取了部分林木进行了年龄的实测，结果表明实测年龄与该方法的相对误差控制在20%以内。本文以年龄为自变量，拟合栎类与杉木的断面积平均生长曲线，反映的是树木平均年龄与断面积的生长过程，而估计年龄是在实测年龄的上下波动，20%的误差对平均年龄的影响不大，可以认为估计年龄对本文的研究结果影响较小，可以应用于断面积的生长建模。