立体几何中动态问题的解题策略

>>>杨春辉

近几年的高考试题中，立体几何中的动态问题多次作为压轴的客观题出现。动态问题的起因大致分为两类：平移与旋转；而要解决的问题主要有三类：一是面积、体积问题，二是角度问题，三是距离问题。解决这类问题需要非常强的空间想象能力和转化能力，解题要在动态中找到“静”的一面，在变中找到“定”的一面，动中求“静”，变中求“定”。

一、几何体表面上的动点间的最短距离问题

例1.已知各棱长均为1的四面体ABCD中，E是AD的中点，P∈CE，则BP+DP的最小值为

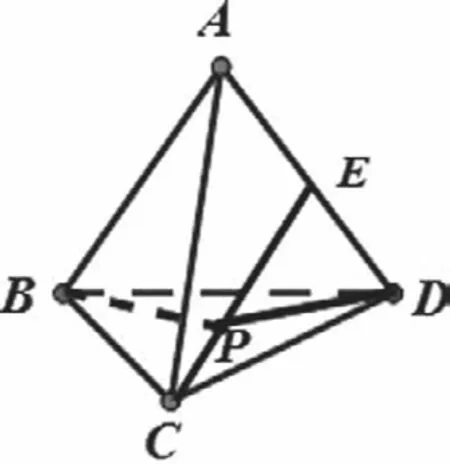
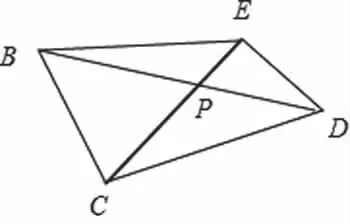
解析：把平面BEC及平面CED以CE为折线展平，三角形CED是正三角形的一半，故在平面DEBC中，连接BD，与EC相交于点P，则DP+BP为最短距离，再利用余弦定理即可得出.

二、动态中与形成的截面的面积有关的问题

例2.长方体 ABCD-A1B1C1D1中，已知 AA1=3，AB=AD=2，棱AD在平面α内，则长方体在平面α内的射影所构成的图形面积的取值范围是_______.

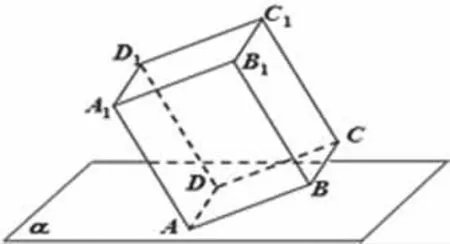
解析：由题意，四边形ABCD和ADD1A1的面积分别为4和6.

若记平面ABCD与α平面所成角为θ，则平面ADD1A1与平面α所成角为-θ.它们在平面α内的射影的面积分别为 4cosθ 和 6cos（-θ）=6sinθ，所以，S=4cosθ+6sinθ=2sin（θ+φ）（其中，tanφ=）.

三、动态中与形成的几何体的体积有关的问题

例3.一个棱长为12的正方体形状的铁盒内放置一个正四面体，且能使该正四面体在铁盒内任意转动，则该正四面体的体积的最大值是______.

解析：如图，设正四面体A-BCD的棱长为x，过A作AO1⊥底面BCD于O1，连接BO1并延

设正四面体A-BCD的外接球的半径为r，

要使正四面体可以在棱长为12的正方体内任意转动，

四、动态中与形成的角有关的问题

例 4.在四面体PABC中，PA=PB=PC=AB，如果PA与平面ABC所成的角等于60°，则PC与平面PAB所成的角的最大值是 .

解析：如图所示，过点P作PO⊥平面ABC于点O，连接OA，OB，OC.取 AB的中点 D，连接OD.则∠PAO是PA与平面ABC所成的角，其大小等于 60°.不妨设 PA=2=AB=PB=PC，则 P O=.因为PD=.所以点O与D必然重合. 可知点C在以O为圆心，AB为直径的圆周上运动（去掉A，B两点）.当且仅当CD⊥AB时，PC与平面PAB所成的角取得最大值 30°.

五、动态中形成与球的体积有关的问题

例5.已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为

A.36π B.64π

C.144π D.256π

解析：如图所示，当C点位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大，设故R=6，则球O的表面积为4πR2，故选：C.

通过以上例题的分析可知，在立体几何中由动态引出的有关距离、面积、体积、角的最值或范围问题，思维难度比较高，对直观想象、数学推理等核心素养的要求很高，解决问题的基本方法有：利用极限位置法，即通过分析图形特征，找出取得最值的位置，再进行计算；在动中找定，引入变量，构建函数模型，通过研究函数的最值解决问题。