银杏落叶期叶片NDVI 值2 种拟合方法比较

周柯妙，林 辉，宋仁飞，蒋 仟，陈忠明，杜 凯

（1.中南林业科技大学 林业遥感信息工程研究中心，湖南 长沙 410004； 2.林业遥感大数据与生态安全湖南省重点实验室，湖南 长沙 410004； 3.南方森林资源经营与监测国家林业与草原局重点实验室，湖南 长沙 410004）

随着遥感技术的不断发展，尤其是近些年来高光谱遥感技术的大力发展，使快速获取植物叶片的的精细光谱信息成为了可能。对银杏Ginkgo bilobaL.叶片的落叶期光谱特征参量进行以宏观上的时间为自变量的曲线拟合，有助于了解银杏落叶期叶片光谱特征参量的变化趋势，从而了解银杏的生长情况，对其进行决策和控制，并为植被的大尺度遥感动态监测提供了方法参考。

国内外学者利用遥感技术对植被的NDVI 进行时间序列监测取得了大量的成果。在空间大尺度遥感数据方面，夏照华、张克斌等人采用多月多分辨率遥感数据，合成NDVI 数据，在加上同时期的降水、温度数据，从多角度分析了近些年NDVI 大尺度的时空分布规律[1]，吴文斌等利用NOAA/AVHRR NDVI 时间序列数据，利用两种比较方法对Savitzky-Golay 滤波法和非对称性高斯函数拟合法进行了比较分析[2]；蒋雪冰等采用MODIS NDVI 影像和野外实测的反射率数据，利用线性内插和扩展卡尔曼滤波组合重构方法进行重构处理[3]；宋盼盼等基于最小二乘原理，采用多项式拟合方法对中稻、晚稻NIR、R、NDVI 3 种植被指数进行时间序列特征曲线拟合[4]； 在地物高光谱遥感方面，卢霞等利用ASD 光谱仪，对浒苔水体的反射率数据进行连续测定，再提取计算浒苔水体的光谱特征参量，进而对其进行时间序列拟合研究[5]；同时，卢霞等还对ASD 光谱仪测定获取浒苔水体的反射率数据，对浒苔藻体时间序列高光谱特征参量进行曲线拟合[6]。但在关于地表植被的NDVI 时间序列模拟的研究中，大部分都是使用的大尺度多光谱遥感数据，少有用地面高光谱数据作分析；而在用地面高光谱数据来分析特征参量的数据模拟研究中，又鲜有对乔木树种的研究。

以银杏为研究对象[7]，利用SVC HR-1024I 全波段地物光谱仪，对银杏落叶期叶片数据进行周期为15 d 的高光谱观测，对获取的高光谱数据进行去重处理，提取特征参数，并分别进行二次函数拟合及ARIMA 时间序列拟合，得到最优拟合方法。

1 材料与方法

1.1 研究区概况及位置图

研究区位于湖南省长沙市天心区中南林业科技大学植物园内，112°59′31″E，28°8′11″N，为亚热带季风气候，四季分明，春温多变，夏秋多晴，严冬期短，暑热期长的特点，适合植物生长。植物园内植物种类繁多，银杏作为主要行道树之一，广泛分布在植物园内。

1.2 实验数据获取及数据预处理

1.2.1 高光谱数据获取

高光谱观测采用的仪器为SVC HR-1024I 全波段地物光谱仪，波长范围350 ～2 500 nm，包含 1 024 个波段，视场有4°标准和25°光纤两种，本次实验选用的是4°标准视场角。

银杏为银杏科、银杏属落叶乔木，4月初发芽，每年9月底至12月为落叶期，叶片逐渐由绿变黄并掉落，至1月初完全落叶。实验选在银杏叶片落叶期（9月中旬至12月中旬）进行，选取3 株健康、生长环境相同的中龄银杏为叶片采集对象，以15 d为观测周期，利用高枝剪对其冠层向阳处叶片进行采集，将采集到的叶片置于保鲜袋，迅速将叶片带到室验室内，进行高光谱测量，每株树观测5 次。将采集到的进行整理与筛选，剔除异常光谱曲线后，选取3 株树的光谱反射率均值为实验数据，得到银杏落叶期各期光谱值（图1）。

图1 银杏落叶期各时期光谱曲线图Fig.1 Spectral curves of Ginkgo leaves in various periods

1.2.2 高光谱数据重叠校正

由于仪器在测量时有的波段进行了重复测量，光谱曲线在波长967 ～1 013 nm 部分有一段重叠曲线，因此需要对原始数据进行重叠校正，使光谱曲线变成一条平滑且无重复点的曲线，校正后结果如图2 所示。

图2 银杏落叶期光谱曲线重叠校正结果Fig.2 Overlapping correction results of spectral curve of Ginkgo leaves in various periods

由图2 可以看出光谱曲线重叠部分已经被去除，光谱波段也由原始的1 024 个减到了960 个。

1.2.3 银杏叶片NDVI 值计算

归 一 化 植 被 指 数（Normalized difference vegetation index，NDVI）是反映作物长势和营养信息的重要参数之一[8]，植物生长状态健康、长势旺盛的时候，其NDVI 值比较高；但当植物处于不健康状态，或者趋于衰老的时候，其NDVI值会随之降低，NDVI 计算公式为：

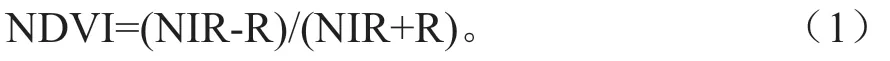
其中，NIR—近红外波段的反射率，R—红光波段的反射率。

不同树种由于反射能力不同，而NIR 与R 所对应的反射率也不一样。对于SVC 全地物光谱仪获取的光谱值数据，目前普遍采用波长719 nm 处的反射率为NIR 处反射率，波长680 nm 的反射率为R 的反射率[5]，据公式（1）计算银杏落叶期各期NDVI 值（表1）。

1.3 研究方法

1.3.1 二次函数拟合法

最小二乘法中的二次函数拟合法，原理是所选择的回归模型应该使所有观察值的残差平方和达到最小[9]，其模型为：对给定的数据列(xi,yi)，i=0，1…，m，满 足y=a0x2+a1x+a2，a0，a1，a2的计算如公式（2）（3）（4）。

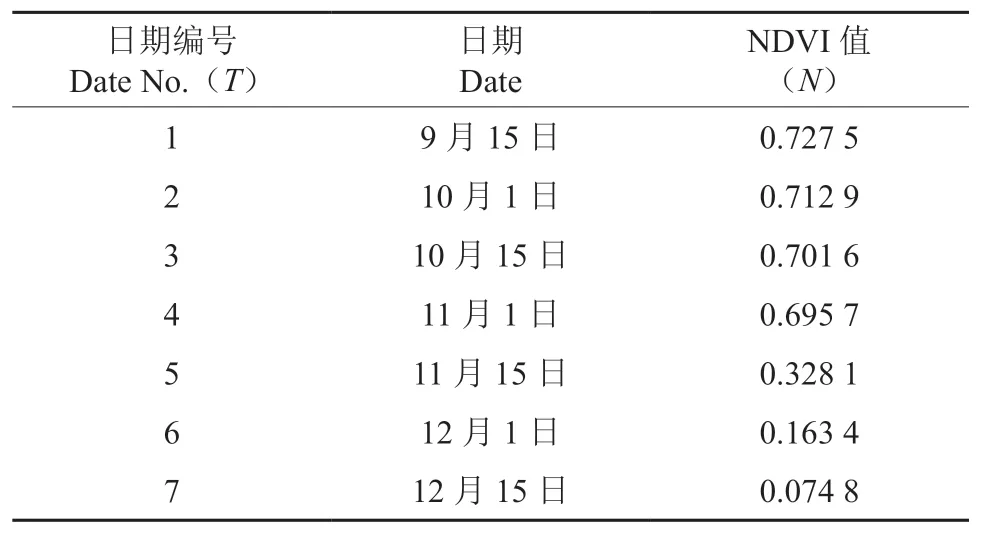
表1 银杏落叶期各时期NDVI 值Table 1 NDVI in the deciduous period of Ginkgo leaves

1.3.2 ARIMA 时间序列拟合法

差分自回归移动平均模型（Autoregressive integrated moving average model, ARIMA）拟合是根据实测的数据[10]，通过对原始不平稳序列进行差分使序列平稳，再通过曲线拟合对系统进行客观的描述，可对时间序列进行分析、预测、决策和控制等[12]。一个ARIMA 过程包括自回归移动平均过程（ARMA）以及ARIMA 过程，其中ARMA 模型有以下三种形式[11]：

一是自回归模型（AR：Auto-regressive），其基本形式为：

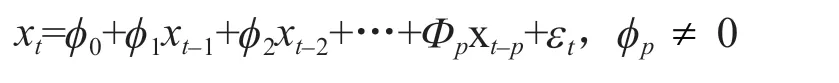
式中εt为白噪声序列，此时称时间序xt为服从p阶的AR 模型；

二是移动平均模型（MA：Moving-average）， 其基本形式为：

式中εt为白噪声序列，此时称时间序列xt为服从q 阶的MA 模型；

三是自回归滑动平均模型（ARIMA），其初始序列一般不具有平稳性，对序列进行d 差分后使序列平稳，其基本形式为：

式中εt为白噪声序列，此时称xt为服从(p,d,q)阶的ARIMA 模型。

1.3.3 零均值化处理

零均值化处理能去除直流分量的影响，避免在后面的处理中引入不必要的分量从而对结果造成影响。零均值化处理计算公式如公式（5）。

—零均值化处理后数据，xi—原始数据，—原始数据平均值。

1.3.4 AIC 准则

最小信息量准则（An information criterion，AIC 准则）是一种考评综合最优配置的指标，也是拟合精度和参数位置个数的加权函数，在模型定阶过程中，使AIC 值达到最小值的值被认为是最优模型阶数。在现实生活中，要求模型越简单越好，通常阶数≤2。AIC 计算公式如公式（6）。

式中n—样本数量，ln—对数运算符，A—残差平方和，p—回归方程中自变量的个数。

2 结果与分析

2.1 二次函数拟合结果

银杏落叶期叶片NDVI 值拟合过程采用Matlab 与Eviews。在Eviews 中 对 银 杏 落 叶 期NDVI 值（N）与其所对应的时间编号（T）进行方程二次函数拟合，根据公式（2）（3）（4）得到的参数结果如表2。

表2 银杏落叶期叶片NDVI 二次函数拟合分析结果表Table 2 Analysis of NDVI quadratic function fitting of leaves of Ginkgo leaves

由表2可知模型二次项系数为-0.022 1，一次项 系数为0.054 7，常数项为0.710 6，即拟合方程为：

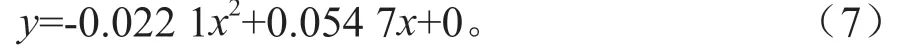
式（7）中：y—NDVI，x—时间编号。

在Matlab 中对运用最小二乘法对银杏落叶期叶片的NDVI 值进行曲线估计得到曲线，如图3所示：

图3 银杏落叶期NDVI 值二次函数拟合结果Fig.3 Fitting results of quadratic function to NDVI values in deciduous period of Ginkgo leaves

如图4 中拟合曲线是一条平滑的曲线，在时间编号范围1 ～3 之间时，预测值与实际值大体相符；在时间编号范围3 ～4.5 之间时，预测值小于实际值，且实际值不是平缓下降，而是在编号4之后才开始有明显的下降趋势；在编号范围4.5 ～7之间，下降的速度慢慢变缓，而在编号4.5 ～6.5之间，预测值略高于实际值。

从拟合的结果看，R2为0.926，说明拟合效果较好；根据两个系数项和常数项的t 统计量取值情况，研究中所用到的NDVI 值个数为7 个，所以这些t 统计量要服从自由度为5 的t 分布，根据查得的t 分布表[11]，当t=5 时，检验水平为0.1、0.05和0.01 时所对应的临界值分别为2.015、2.571 和4.032，本次拟合中3 个t 统计量只有常数项的t 统计量显著，2 个系数项的t 统计量均远小于检验水平的临界值，且常数项的P值小于0.05，而两个系数P值远大于0.05，这说明所构建模型拟合结果具有随机性[13]。

2.2 ARIMA 时间序列拟合结果

在Matlab 中利用公式（5）对原始NDVI 数据进行零均值化处理，得到一组新的数据NDVI。在SPSS 软件中对得到的新的数据组进行单样本K-S检验，看数据组是否服从正态分布，检验结果如表3 和表4 所示。

表3 K-S 检验描述性统计量表Table 3 K-S test descriptive statistical scale

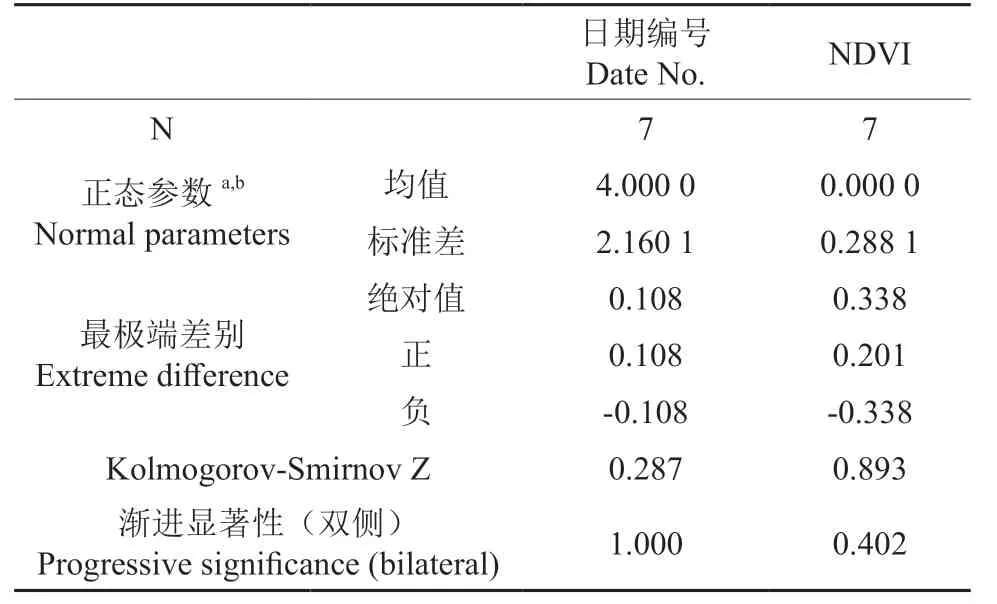
表4 单样本Kolmogorov-Smirnov 检验Tab.4 Single sample Kolmogorov-Smirnov test

由表3 表4 可知，数组双侧渐进显著性均大于0.1，数组服从正态分布。

对数列进行模型识别，即计算时间序列其自相关函数和偏自相关函数的拖尾及截尾情况[14]。自相关系数（ACF）指的是同一事件在两个不同时期之间的相关程度，目的是度量过去的事件对现在的时间所造成的的影响；偏自相关系（PACF）指的是单纯考虑单独事件某一时期对另一时期的影响或相关程度，只考虑事件两个时期之间的相关性程度。ARMA 模型三种形式的相关性特征及模型选择，如表5 所示。

由于序列本身具有不平稳性，先将数据进行差分使序列平稳，在Matlab 软件中差分后的样本序列的自相关系数和偏自相关系数，如图4 和图5 所示：

表5 ARMA 模型相关性特征Table 5 ARMA model correlation characteristics

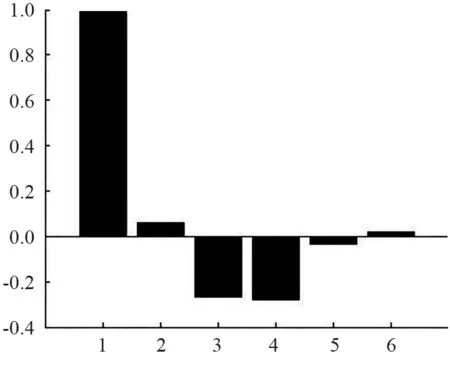
图4 样本数据自相关系数Fig.4 Sample data autocorrelaion coefficient

图5 样本数据偏自相关系数Fig.5 Sample data partial self-correlation coefficient

根据NDVI 值零均值化后的样本序列所计算得到的自相关系数以及偏自相关系数结果来看，自相关函数自延迟1 阶后，在2 倍标准差的范围内波动，表明数列短期内相关，因此自相关系数可视为拖尾；偏自相关函数延迟1 阶的偏自相关函数显著大于标准差，其他的自相关系数在2 倍标准差范围内做小值的波动，非零相关系数衰减为小值的过程十分突然，自延迟3 阶后相关系数衰减为0，即偏自相关系数视为截尾；根据ARMA 模型的相关特征，初步将模型视为AR（3）模型，由于序列组数据比较少，为了提高拟合的准确性，具体模型的识别及定阶通过AIC 准则进行计算确定[15]。

AIC 准则计算根据公式（6）在Matlab 软件中进行，计算结果如表6：

由表6 可知，当p=2，q=2 时，AIC 值最小，此时模型为最优，即ARIMA 过程中的ARMA 过程为ARMA（2，2）模型，加上一次差分过程，综合模型为ARIMA（2,1,2）。

采用Matlab 软件对模型进行ARIMA 时间序列曲线拟合得到曲线，如图6 所示。

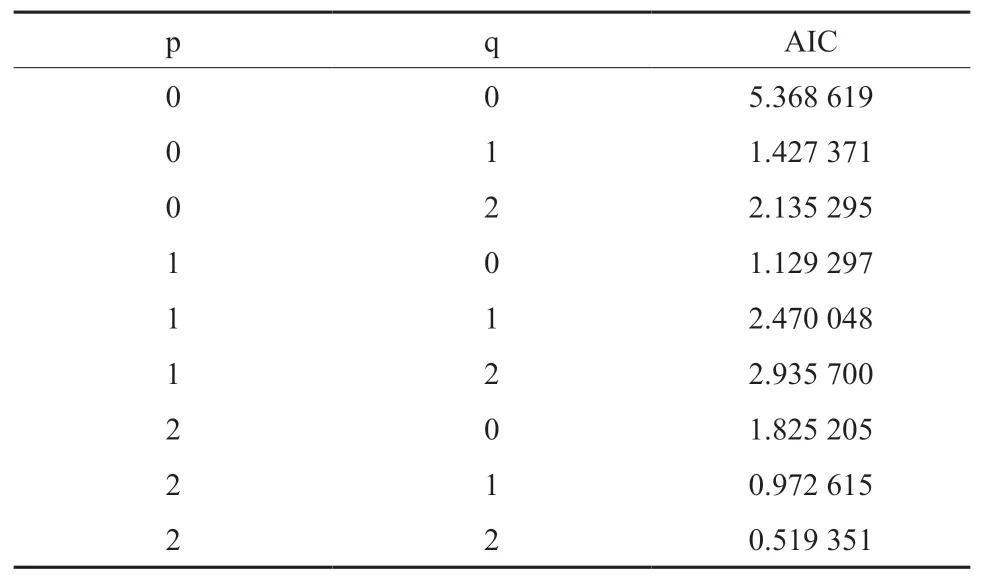
表6 AIC 计算结果Table 6 AIC criteria to calculate the results

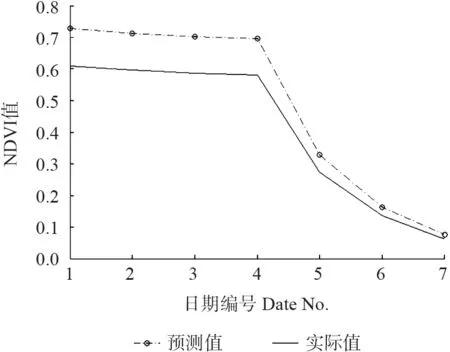
图6 银杏落叶期NDVI 值ARIMA 时间序列拟合结果Fig.6 Deciduous period of Ginkgo leaves NDVI values of ARIMA time series fitting results

采用Eviews 软件对模型进精度评价，R2为0.811，拟合曲线与实际曲线走势一致，拟合效果较好。

3 结论与讨论

以中南林业科技大学校植物园为研究区，在银杏的落叶期内，以健康生长的中龄银杏叶片为研究对象，以半个月为周期，利用SVC HR-1024I全波段地物光谱仪对其进行定点的高光谱数据采集，对采集的数据进行数据预处理后，根据计算观察到的NDVI 趋势，选用二次函数曲线拟合和ARMA 时间序列拟合法对各期的NDVI 值进行拟合，得到银杏落叶期间NDVI 值的动态变化规律，得出的主要结论如下：

1）二次函数拟合结果为NDVI=-0.022 1T2+ 0.054 7T+0.711，决定系数R2为0.926，t 值不显著，样本结果随机性大，不具广泛性；

2）ARIMA 时间序列拟合结果为ARIMA（2,1,2）模型，R2为0.811，样本结果与实际趋势大致一致，拟合效果较好；

3）二次函数拟合和ARIMA 时间序列拟合都能较好地对本次实验数据进行拟合，但由于二次函数拟合结果具有很大的随机性虽然二次函数拟合结果的决定系数大于ARIMA 时间序列拟合结果，但二次函数拟合结果具有很大的随机性，总体上讲ARIMA 时间序列拟合的方法要优于二次函数拟合方法。

基于高光谱遥感数据的乔木树种动态一直是研究的一个难点和重点。本研究采用地面实测高光谱数据，通过两种方法对银杏落叶期叶片NDVI值进行曲线拟合，为植被大尺度的高光谱空间监测提供方法参考，在下一步的研究中，将尝试用其他高光谱特征参量对银杏及其他树种的光谱特征参量进行年度上的微观变化分析。