基于逆系统解耦的MSCSG姿态测量方法

于春淼，汪洲，任元，*，王卫杰，樊亚洪

（1.航天工程大学 研究生院，北京101416； 2.航天工程大学 宇航科学与技术系，北京101416；3.北京控制工程研究所，北京100190）

随着空间航天器事业不断发展，卫星快速发射需求越来越高，体积越来越趋近于小型化［1-2］，而姿态测量与控制一体化是航天器实现小型化的有效手段之一［3-4］。本文研究对象磁悬浮控制敏感陀螺（Magnetically Suspended Control and Sense Gyroscope，MSCSG）［5-6］是将姿态控制与姿态测量功能合二为一［7］的新概念陀螺，其具有低噪声［8］、微振动［9］、非接触［10］等突出优点，也是有效解决高分侦察技术所面临甚稳超静［11］姿态控制难题的理想选择。MSCSG检控一体的特点可以有效减小航天器体积、重量和功耗［12］。

在基于磁悬浮惯性器件的航天器姿态测量研究上，国内外开展了一系列研究。刘彬等［13］基于磁悬浮陀螺飞轮，提出一种将输出控制力矩和敏感姿态角速度于一身的方案，采用洛伦兹力磁轴承（Lorentz Force Magnetic Bearing，LFMB）进行五自由度支承，其产生的磁力与电流成线性特性，从而达到测量姿态的目的，但该方案未得到实验验证；文献［14］中加拿大Bristol宇航有限公司研制了一种挠性陀螺飞轮，该装置可以在输出三自由度的控制力矩的同时敏感航天器两自由度的角速度，但该陀螺测量精度有待提升；房建成和任元［15］提出一种新型磁悬浮陀螺飞轮，可以对航天器同时输出三自由度控制力矩和敏感两自由度姿态角速度，可减小航天器姿态控制系统的体积。但是磁悬浮陀螺飞轮的转子转动与平动之间存在耦合，从而也导致了该陀螺测量角速度精度有限；房建成等［16］提出利用双框架MSCMG进行姿态测量，针对测量得到的两轴姿态角速度间存在耦合的问题，提出了动态解耦补偿方法，进一步提高了陀螺的测量精度，但是该动态解耦方案在解算化简过程中采用了高阶近似，精度还有提升的空间。

此外，模糊解耦［17］、神经网络解耦［18］、滑模解耦［19］等方法也被用于抑制两自由度姿态控制耦合。但这些方法都需要大量的计算机资源分配，需要大量的数据进行学习，因此在航天器姿态测量系统中通常受到限制。逆系统［20］方案简单、直观，执行起来相对简单，物理概念清晰，且易于理解和分析，同时对于MSCSG来说，数学模型建立较为方便，更适合采用逆系统。目前逆系统通常应用于控制，测量方面的应用还未见报道。

MSCSG是由航天工程大学2015年首次提出的一种新概念陀螺仪，并于2018年研制成功国际首台原理样机［5，7］。本文将在原理样机研制的基础上，结合控制MSCSG径向偏转的LFMB的工作原理建立动力学模型，推导基于MSCSG的姿态角速度测量方法，并分析MSCSG 2个测量轴之间的耦合关系，为提高航天器姿态角速度的测量精度，本文采用逆系统对其进行了解耦，在抑制2个测量轴之间耦合的同时提高MSCSG的测量精度。

1 M SCSG工作原理及动力学建模

1.1 工作原理

如图1所示，MSCSG由上、中和下陀螺房、转子、电机、位移传感器、力矩器、轴向磁轴承与径向磁轴承等部分组成。其中：转子是MSCSG结构中的核心部件，也是MSCSG质量分布最集中的部分。电机、轴向磁轴承、径向磁轴承与力矩器共同来控制转子的六自由度，电机用来控制转子转速，即转子轴向旋转自由度；轴向磁轴承控制转子稳定悬浮，即转子的轴向平动自由度；径向磁轴承控制转子的径向两平动自由度。力矩器采用LFMB结构控制转子径向偏转两自由度。径向磁轴承与轴向磁轴承均采用了球面结构，可保证转子发生偏转后的磁极面依然均匀，不至于因偏转而产生径向干扰力矩，从结构上消除了轴向和径向3个平动方向对径向2个偏转方向的耦合。位移传感器用于检测转子的位置变化信息；此外上、中、下陀螺房用于支承定子构件，同时还具有密封防护的作用。

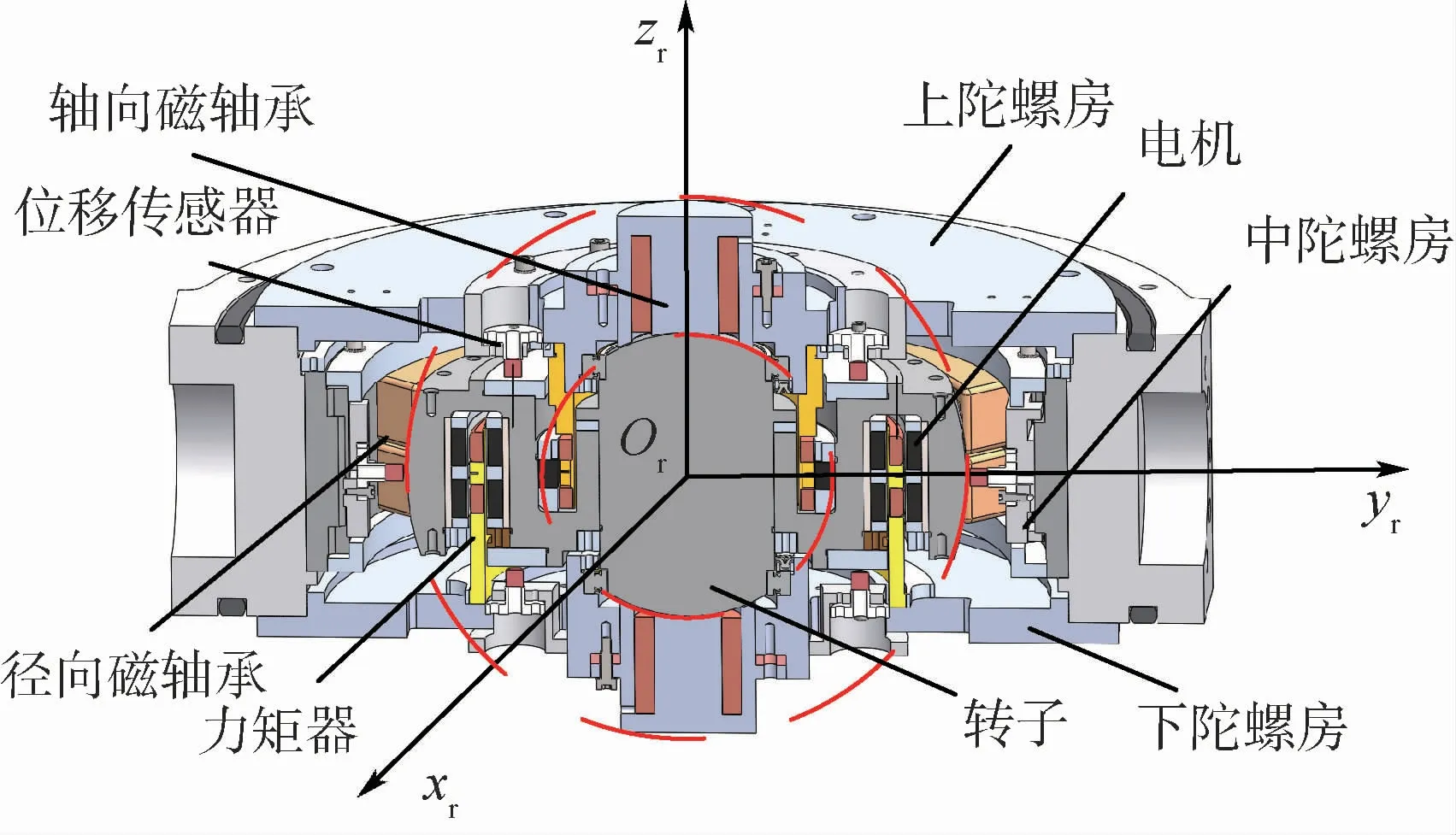
图1 MSCSG陀螺房结构示意图Fig.1 Schematic diagram of MSCSG gyro room structure

1.2 动力学建模

MSCSG安装在航天器上，其定子相对惯性系具有3个转动自由度，其转子具有3个转动自由度和3个平动自由度。为了便于建立MSCSG动力学模型，定义陀螺初态为计时零时时刻，高速稳定旋转的转子悬浮于定子腔体中心，转子、定子球形包络面的球心重合，定子相对于惯性空间角速度为零的状态，同时定义坐标系如下：

惯性坐标系Oi-xiyizi：将地心赤道坐标系作为惯性坐标系，地心Oi为坐标原点，xi轴指向春分点，zi轴指向地球北极，与yi轴构成右手坐标系。

定子坐标系Os-xsyszs：定子坐标系与陀螺定子固连，原点Os位于定子球形包络面几何中心，取径向磁轴承的垂直平分线作为zs轴。

转子坐标系Or-xryrzr：与转子固连，但不随转子转动，原点Or位于转子几何中心，zr轴为转子旋转轴，当转子位于平衡位置时，Or-xryrzr与Osxsyszs重合。

依据安培力定律，LFMB产生的电磁力表达式为

式中：f为产生的电磁力；B为磁感应强度；L为与磁场垂直方向的线圈长度；I为线圈中的偏置电流。

LFMB结构如图2所示，α和β分别是转子绕xr轴、yr轴偏转的角位移，LFMB骨架中心与转子中心重合。其与下陀螺房固连，上面安装有上、下两层磁钢，为保证能够形成闭合磁场，内、外磁钢的充磁方向相反。同时LFMB骨架上缠绕了4组相同匝数的线圈，4组线圈保持均匀分布，每相对的2组线圈分别控制一个径向偏转自由度。

α和β分别为转子绕xs、ys轴偏转角的大小，lm为LFMB定子半径，ls为4个位移传感器所在圆的半径。

当图2中的线圈通入电流时，将产生垂直于线圈与磁场方向的安培力，上、下2个线圈的合力大小为

式中：N为LFMB中线圈匝数。

将式（2）改写为

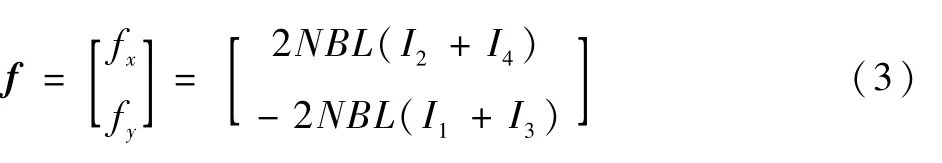
式中：I1、I3分别为xs轴正、负线圈上等大、反向的电流；I2、I4分别为ys轴正、负线圈上等大、反向的电流。则有I2＝I4＝Iα，I1＝I3＝Iβ，其中：Iα、Iβ分别表示xs轴、ys轴的偏置电流，此时相对的线圈将产生等大、反向安培力。从而有

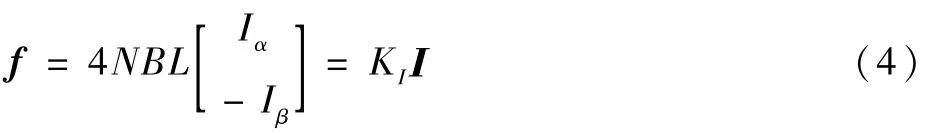
其中：KI＝4NBL为电流刚度。

由此可得LFMB提供的xs、ys方向偏转力矩为

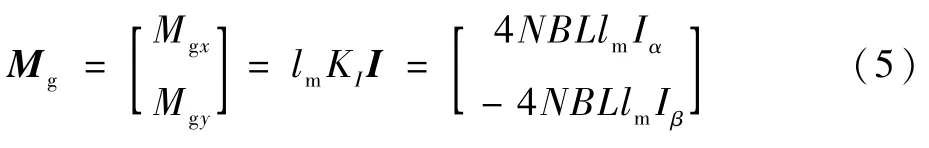
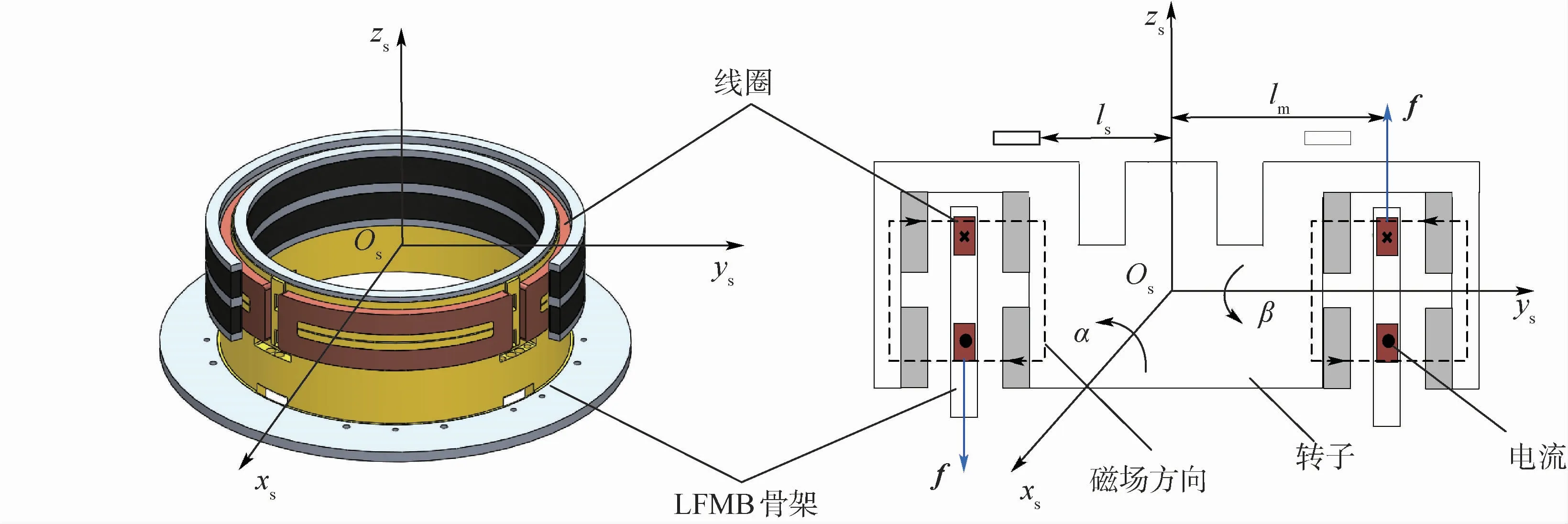
图2 LFMB结构原理Fig.2 LFMB structure principle

为了获得足够大的角动量以增加输出转矩和姿态灵敏度，MSCSG设计成扁平状。当转子高速运行时，陀螺效应十分显著，因此陀螺容易产生失稳。如果控制方法中没有考虑到这一点，会导致高速转子的失稳。控制器相位滞后，会对高速转子稳定性产生影响。为保证MSCSG转子控制系统的稳定性，本文采用了一种交叉反馈补偿的PID控制器来解决上述问题，GPID用于分散PID控制，Gcr（s）用于交叉反馈补偿，控制器设计为

Gc（s）＝GPID（s）＋Gcr（s）＝

式中：kP为比例增益；kI为积分增益；kD为微分增益；kL和kH分别为低通滤波器和高通滤波器的系数；τL和τH分别为2个滤波器的时间常数；E2为2×2的单位矩阵；s为拉普拉斯算子；Ω为转子绕zr轴旋转的速度；Cr为交叉反馈矩阵，其表达式为

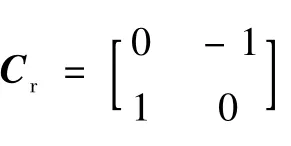
为实现电流比例反馈控制而获得更宽的带宽，功放系统可用一阶环节建模，表示为

式中：kw为功放增益；ωw为截止频率。

传感器信号的反馈回路上，通过调理电路和抗混叠滤波器传至数字控制器，表示为

式中：ks传感器增益；ωs为抗混叠滤波器的截止频率。

2 两自由度姿态测量方法

MSCSG转子控制系统由控制器、信号调理电路、电磁铁转子和传感器组成，见图3。当转子沿轴向高速转动时，靠轴向磁轴承产生的磁场悬浮；当发生转动时，转子将沿xr或yr方向产生偏转角，高精度传感器将检测到转子位置的变化，位移信号经由信号调理系统传递至控制器，控制器将会在xr或yr方向的线圈上施加相应控制电流，改变磁场内作用导线的电流大小并生成作用于转子的恢复力，使转子重新回到起始位置；最后通过测量观察线圈上的控制电流即可推导出MSCSG的角速度。MSCSG的角速度测量主要与径向转动自由度有关，所以下文将通过分析转子径向xr和yr方向的偏转自由度来建立动力学模型。

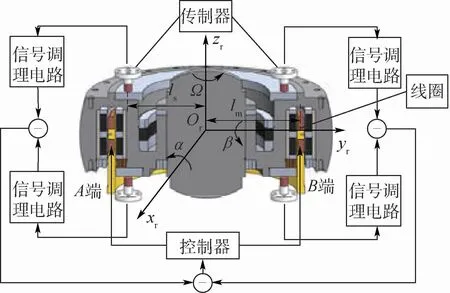
图3 MSCSG转子结构示意图Fig.3 Schematic diagram of MSCSG rotor structure

根据刚体运动的动量矩定理，有

式中：Mu为转子输出的控制力矩；ωir为转子的牵连角速度；Hr为转子系下转子的角动量，可以表示为

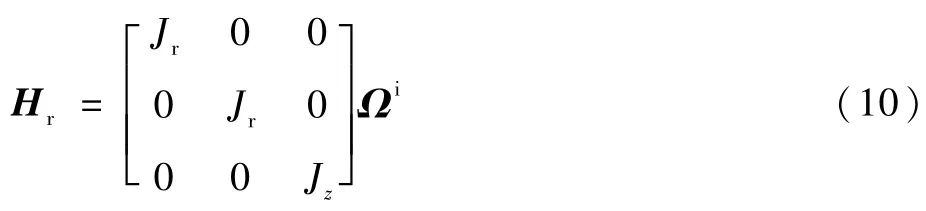
其中：Jr为转子的径向转动惯量；Jz为转子的极转动惯量。Ωi为转子绝对角速度，可表示为

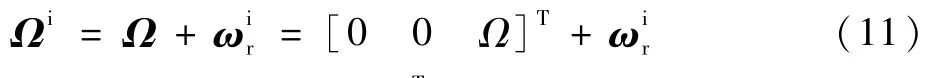
其中：Ω＝［0 0 Ω］T为转子相对于转子坐标系的角速度。

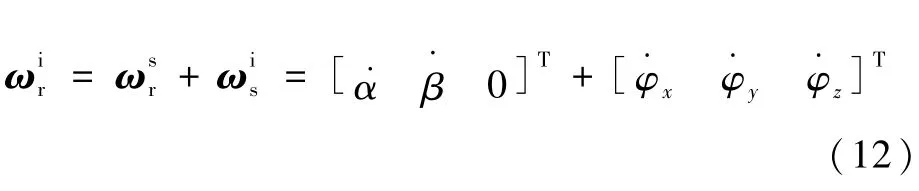
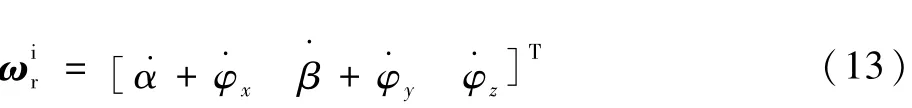
从而有

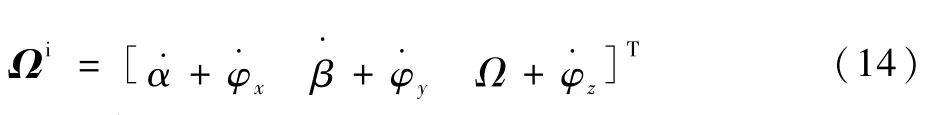
代入式（10）得

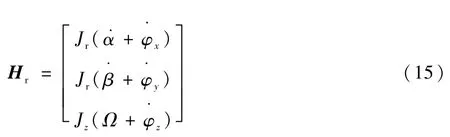
对式（15）求导得

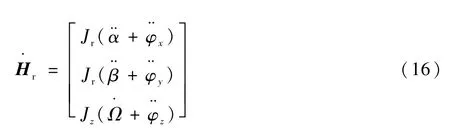
又

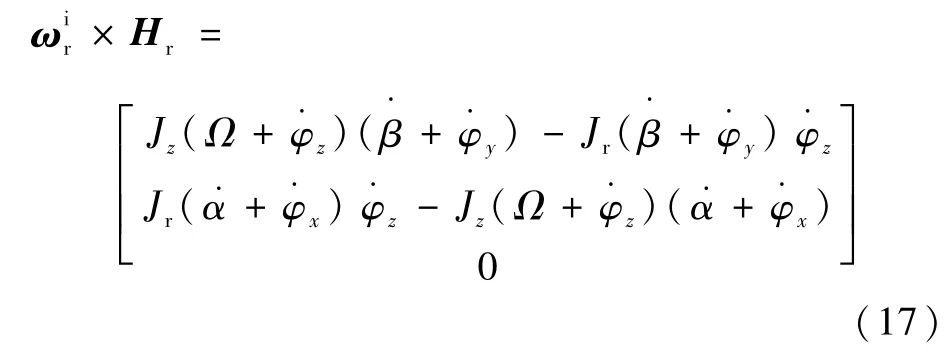
将式（16）、式（17）代入式（9）中得M u＝

为求磁悬浮转子所受的合外力矩，令式（18）中的φ·x，φ·y，φ·z，Ω·＝0。可得

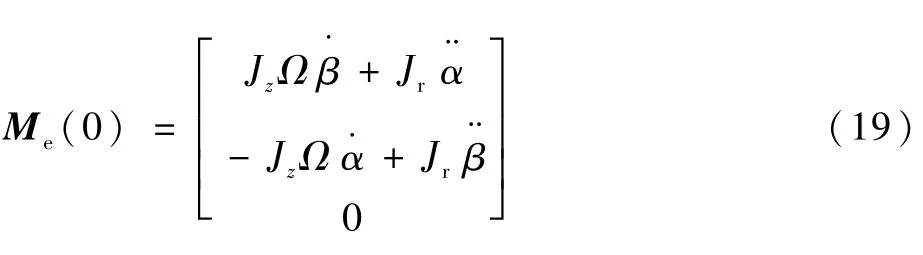
从式（18）中减去Me（0），同时假设航天器在zs轴上转速为零，即可得陀螺转子径向两轴方向上的输出力矩为

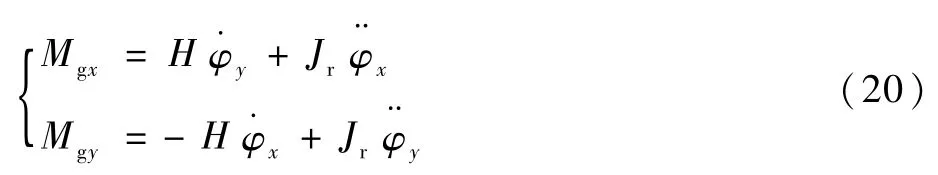
式中：Hφ·y、Hφ·x分别为xs轴和ys轴方向上的陀螺进动力矩项，分别为xs轴和ys轴方向上的惯性力矩项。由于转子通常运行在很高的转速下，具有很大的角动量，而航天器的姿态角加速度很小，这样，作为微小量，可忽略惯性力矩项，则有

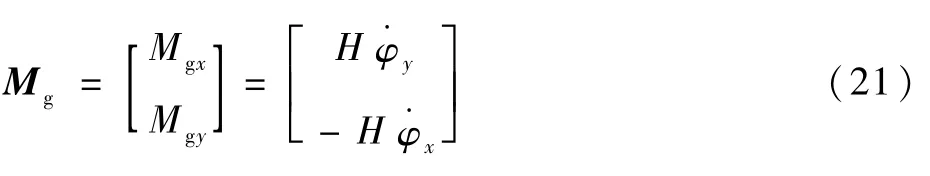
对式（21）进行拉普拉斯变换得

根据牛顿第二定律和陀螺技术方程，广义坐标系中转子动力学方程描述为

对式（24）进行拉普拉斯变换，可得

通过前面的一系列设计，结合每个环节的逻辑利用框图将姿态测量原理展示出来，结果如图4所示。

图4 姿态测量系统原理框图Fig.4 Principle block diagram of attitude measurement system

图4为包含以上各个环节的姿态测量系统原理框图，利用式（6）所设计的控制器，磁轴承控制器可很好地补偿外界施加力矩，姿态角速度计算式为

由图4可得，从φ（s）到φ＾（s）的角速度测量传递函数为

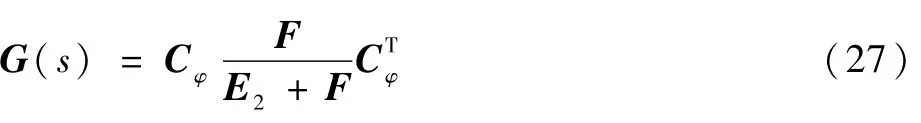
式中：F＝KsGcGwKI lmGg；Cφ为一个常数变换矩阵，其表达式为

结合式（19）、式（26）和式（27）得

式中：I＝（Iα，Iβ）为检测得到的电流结果。代入式（28），可以由测得的电流计算得出MSCSG的两自由度姿态信息。

3 两自由度姿态测量解耦方法

3.1 耦合分析

联立式（4）、式（5）和式（20）得

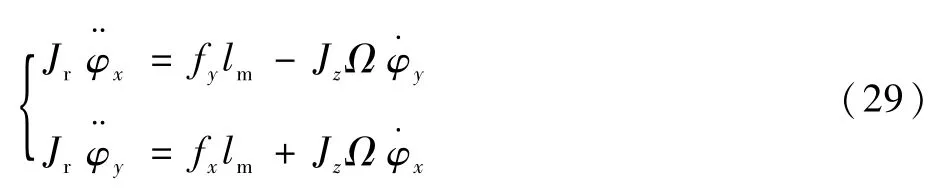
式（4）改写为

同时还有如下关系：

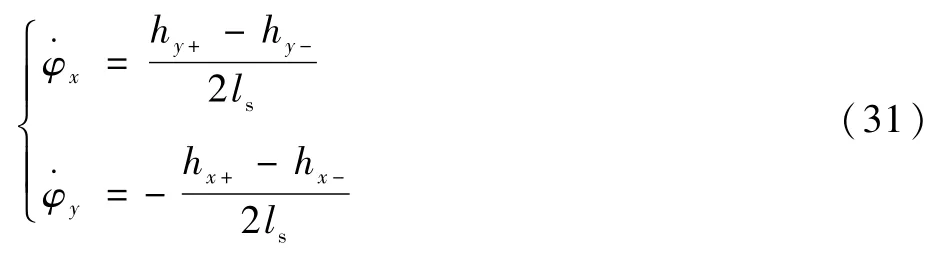
式中：hx＋、hx－、hy＋、hy－分别为xr轴和yr轴正、负方向位移传感器的测量值，并且满足hx＋＝－hx－＝hx与hy＋＝－hy－＝hy的关系，所以有

将式（32）代入式（29）得

即

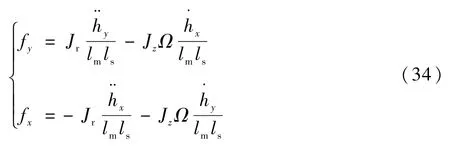
以xs轴方向为例，当Ω＝0时，fx是hx变量的函数，即xs轴与ys轴不存在耦合；当Ω≠0时，fx是hx、hy这2个变量的函数，xs轴与ys轴存在耦合。

3.2 利用逆系统对两自由度姿态测量解耦

由于解耦的目的是弱化径向两偏转自由度间的 耦 合，因此以φx、φy为输出变量，即Y＝［y1y2］T＝［φxφy］T；同时，把Iα、Iβ当作控制变量，也就是U＝［u1u2］T＝［IαIβ］T；然后把在径向xs轴与ys轴方向上的测量值hx、hy及他们的一阶导数作为状态变量，即X＝故 原系统Σ可写成

式中：f（X，U）和矩阵C可以表示为

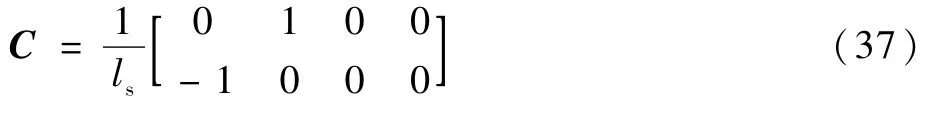
根据逆系统理论，系统输出变量Y＝［y1y2］T＝［φxφy］T对时间进行微分，直到导数中包含控制变量U＝［u1u2］T＝［IαIβ］T为止，得

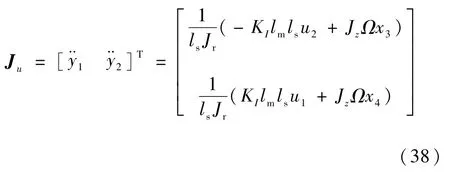
因此，雅可比矩阵D为

从而，通过计算可以得到

令det（D）＝0，由于电流刚度KI≠0，所以得lm＝0，但lm值恒为正数，所以det（D）≠0在系统中始终满足。因此系统的相对顺序是 α ＝［α1α2］T＝［2 2］T，满足α1＋α2＝4≤n（n为状态变量的数量）。因此，根据逆系统理论，可以得出原始系统的逆存在的结论，逆系统可以写为

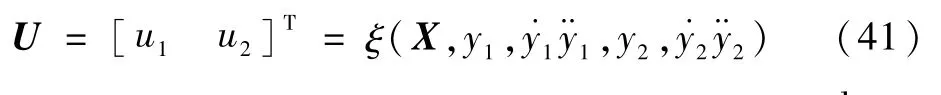
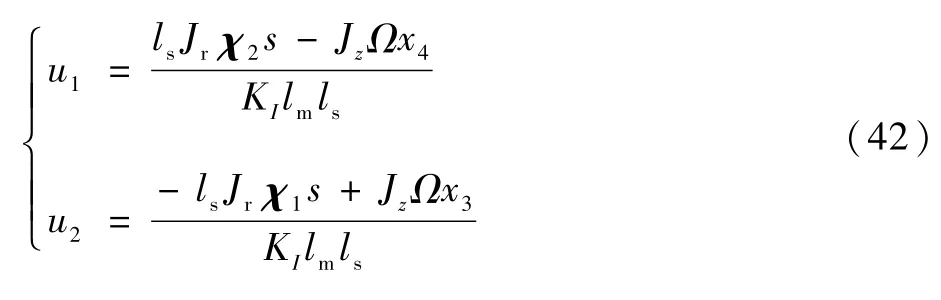
将原系统与求得的逆系统相连接，可以得到一个伪线性系统，如图5所示。从而达到了降低径向两自由度偏转之间的耦合，在一定程度上提高了航天器姿态测量的精度。

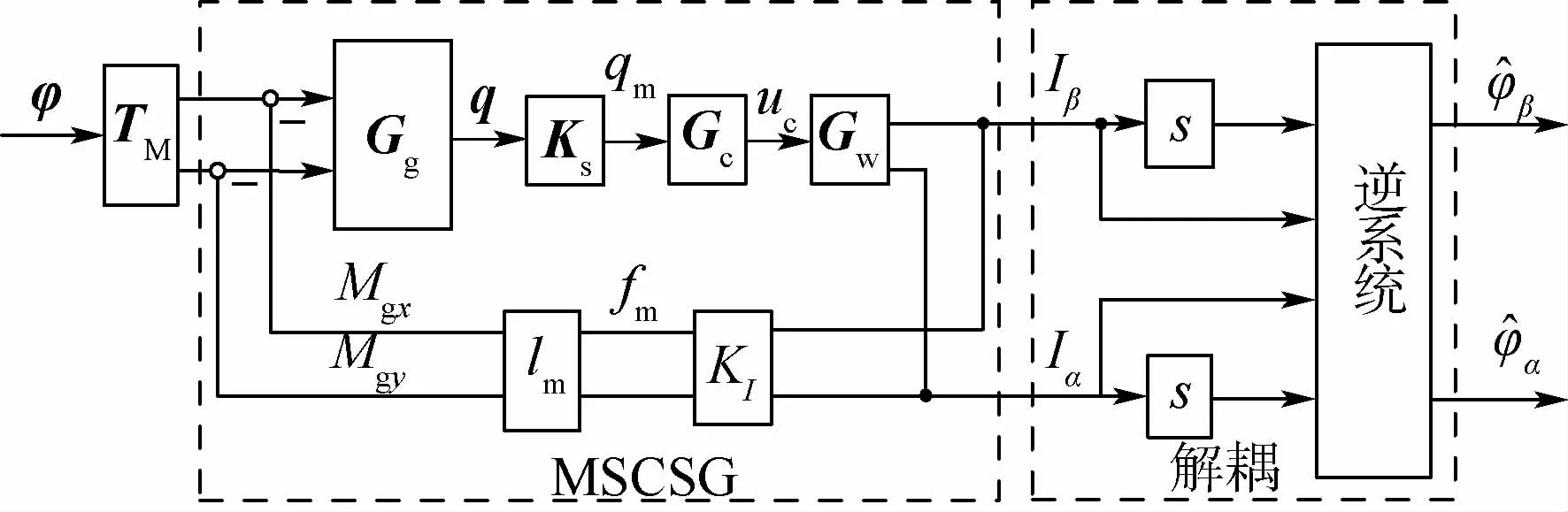
图5 采用逆系统解耦的MSCSG原理示意图Fig.5 Schematic diagram of MSCSG principle with inverse system decoupling

4 逆系统解耦测量仿真验证

为了验证本文方法在实际中的有效性和可行性，通过MATLAB中的Simulink模块对MSCSG样机进行建模并进行敏感解耦仿真验证。

MSCSG样机模型的部分仿真参数如表1所示。图6所示是给卫星的y轴输入振幅为1、频率为10 Hz、20 Hz的正弦角速度信号后的仿真结果。经过仿真得知，当输入频率为10 Hz时，传统方法的测量误差为5.01%，采用逆系统解耦后的测量误差为0.74%；当输入频率为20 Hz时，传统方法的测量误差为7.09%，采用逆系统解耦后的测量误差为0.63%。

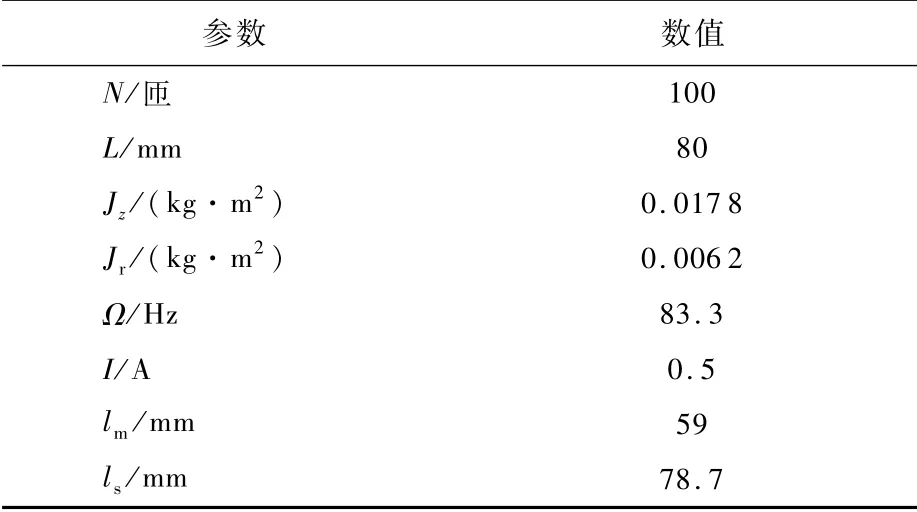
表1 M SCSG系统仿真参数Table 1 M SCSG system sim u lation parameters

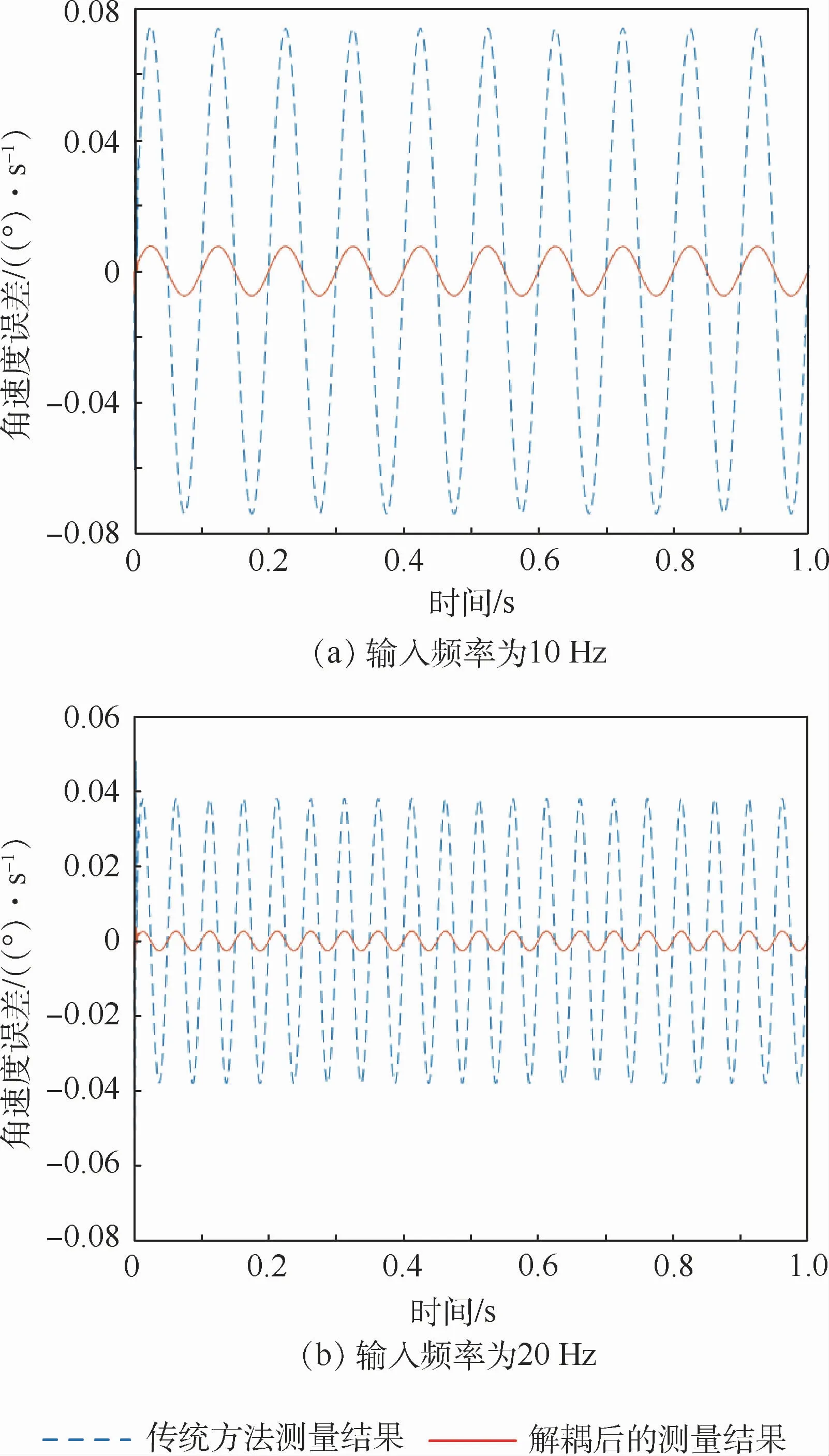
图6 两种方法在输入频率为10Hz和20Hz时的测量误差比较曲线Fig.6 Comparison curves of measurement errors between two methods at input frequency of 10Hz and 20Hz

通过比较可知，相比于传统方法而言，采用逆系统解耦后的测量结果更为精确，测量误差可提升1个数量级，随着输入频率的增加，本文提出的方法对提升测量精度的效果越加明显。

为了验证本文提出解耦方法的有效性，同样给卫星的y轴输入振幅为1、频率分别为10 Hz、20Hz的正弦角速度信号，结果如图7所示。经过仿真得知，当输入频率为10 Hz时，传统方法的耦合可达4.10%，而采用逆系统解耦后的耦合可减小至0.37%；当输入频率为20Hz时，两种方法的耦合分别为9.71%和0.43%。由此可见，本文提出的解耦方法相对于传统方法具有很明显的解耦功能，同时随着输入频率的增加，解耦效果也越加明显。

图7 两种方法在输入频率为10Hz和20Hz时的测量耦合比较曲线Fig.7 Comparison curves of measurement coupling between two methods at input frequency of 10Hz and 20Hz

5 结 论

1）传统测量方法未采取解耦措施，直接通过忽略惯性力矩项求得航天器两自由度姿态信息，使得MSCSG测量精度低。在给航天器输入频率为10 Hz和20 Hz的姿态角速度时，经过逆系统解耦测量精度可提高一个数量级。且随着输入频率的增加，MSCSG测量精度越来越高。

2）采用逆系统解耦，可以很好地降低MSCSG 2个测量轴之间的耦合，在航天器y轴输入频率为10 Hz和20 Hz的姿态角速度时，航天器x轴的耦合可分别降低3.73%和9.28%。且输入频率越大，解耦效果越明显。