基于气动导数的类X-37B飞行器纵向稳定性分析
张庆,叶正寅
(1.西安航空学院 飞行器学院,西安710077; 2.西北工业大学 航空学院,西安710072)
随着日益频繁的空间应用和太空探索活动,人类对廉价、快速和可靠性高的天地往返运输系统的应用需求日趋迫切[1-2]。比较而言,跨大气层轨道飞行器是可重复使用天地往返运输器中比较独特的一种布局形式,其具有较大的气动升阻比,强大的气动舵面操控能力和横向机动能力,较好的再入飞行热、力学环境条件和可重复使用能力,能够在火箭推力作用下跨越大气层后在地球卫星轨道上运行,并像飞机一样水平着陆在地面跑道上[3-5]。据公开资料显示,截至目前,X-37B至少进行了5次太空飞行试验,最近的一次于2017年9月9日发射升空执行“轨道试验飞行器-5”任务,2019年10月27日返回肯尼迪航天中心,总停留时间780天,打破了之前“轨道试验飞行器-4”任务创下的在轨停留718天的X-37B飞行时长纪录。该飞行器在轨运行2年多,还能像普通飞机一样在机场跑道着陆[1,5]。其设计活动可见范围也极大,可从地面一直到外太空轨道,这也是X-37B任务的关键所在[5]。与飞船等传统再入飞行器相比,这类新型再入飞行器在机动性能和可重复利用方面具有更大的优势,已成为各航天大国研究的热点和天地往返运输系统的主要发展趋势[1,6]。但是,由于这类再入飞行器气动布局形式复杂,操纵舵面多,飞行弹道也采用升力式模式,相对于传统的飞行器来说,出现了一系列新的气动设计难点问题,气动设计的复杂程度和难度都非常大[7-8]。
对于可重复使用的跨大气层轨道飞行器来说,其巨大的性能优势的背后是非同一般的技术复杂程度[9-12]。在空气动力学方面,跨大气层轨道飞行器的飞行速度范围涵盖亚、跨、超声速到高超声速,飞行高度从地面延伸到大气层外,在如此巨大的飞行速度和高度跨越中,马赫数效应、黏性效应、气动加热效应、稀薄气体效应和真实气体效应等复杂的因素彼此交错,给气动力评估和稳定性分析带来了很大的困难和挑战[1,8,12]。如何找到合理的气动布局和气动外形,使其既能够满足自主进场着陆、高超再入热防护和火箭发射整流罩尺寸限制,又可以在整个飞行包线内获得理想的气动力、有效的操纵和满足降落机场条件的起降性能是保障中国类似再入飞行器顺利研制成功的先决条件和关键任务之一[1-2]。在气动力性能预测方面,高超声速飞行器与传统飞行器的最大区别在于地面试验设施无法完全再现实际的飞行环境。因此,如何预测飞行器实际飞行环境中的气动性能参数是一项重要的工作[11-12]。目前,唯一的技术途径是:通过风洞试验获得有限条件下的气动性能参数,运用CFD计算模拟风洞环境和实际飞行器飞行环境下的气动参数,获得它们之间的差异,将风洞试验数据外推到实际飞行所需的气动参数[12]。
在气动参数外推的过程中,存在着很多不确定性因素,如何考虑这些不确定性因素的影响是一个一直困扰着气动工作者的难题,目前仍待攻克[10-12]。长期以来,一方面,人们努力提高风洞试验和CFD计算的精度,降低不确定性散布;另一方面,人们也在不断深入探索流动机理,努力摸清传统上没有认识到的影响因素,从而提高预测的精确程度。但是在实际飞行过程中,飞机的运动方式很复杂,会受到诸多因素(包括马赫数、运动频率和运动幅值等)的影响。为了考察此类飞行器随这些因素的变化规律,本文以类似X-37B的典型跨大气层轨道飞行器为例,对这些问题进行了探索性的研究,系统地分析了纵向气动导数随主要运动参数的变化规律,探讨了此类飞行器气动导数求解时的关键影响因素,希望能为中国未来类似轨道器的动力学分析、建模和控制律设计提供参考和指导。
1 计算方法及算例验证
GMFlow是笔者课题组开发的柔性体动力学问题求解程序,该程序包括网格模块、CFD模块和应用模块,可以计算亚声速、跨声速、超声速及高超声速等大速域范围的流动,也可以求解从二维翼型、翼身组合体到带增升装置的三维全机模型等复杂外形的绕流问题,除此之外,还可以用来模拟六自由度多体分离、静气动弹性及动气动弹性等耦合问题[13]。本节主要验证程序对高超声速强迫运动钝锥(所选模型的头部钝度为dN/dB=0.20,dN和dB分别为钝锥头部和尾部的直径)的纵向动态稳定性参数的计算能力,其中非定常流场求解部分采用基于Spalart-All maras湍流模型的有限体积法,强迫运动的网格变形方法为弹簧网格变形方法。首先,用GMFlow计算了该钝锥在马赫数为6.85时,不同平均迎角下进行强迫俯仰运动的非定常气动力变化情况。然后,将纵向阻尼导数提取出来,计算方法详见第2节。最后,将计算结果与采用内伏牛顿流理论计算的结果及试验结果[14-16]进行对比。
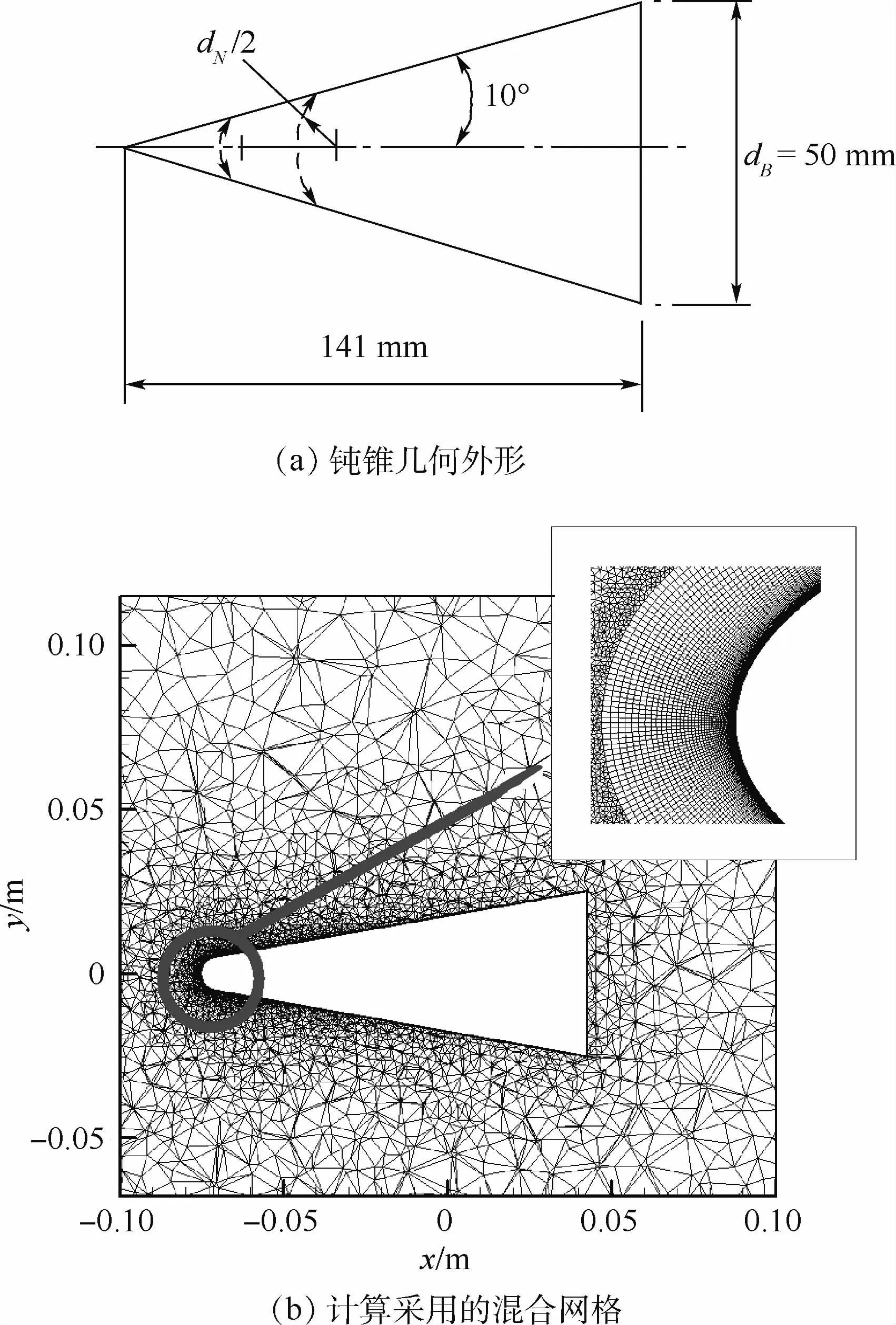
图1 钝锥的几何外形和计算采用的混合网格Fig.1 Blunted cone’s geometric profile and hybrid mesh for computation
图1(a)为10°钝锥的几何外形,本节所选模型的头部钝度为dN/dB=0.20,重心与钝锥顶点距离为钝锥总长度的70%。图1(b)为钝锥初始时刻对称面的网格分布情况,重心在原点处,俯仰轴为y轴。流场网格是混合网格,其中附面层是四棱柱网格,第一层高度为1.0×10-6m,一共31层,其他区域是三棱锥网格。可知,附面层网格质量保持较好,正交性也保持较好。图2为3种方法(试验、内伏牛顿流理论及程序求解)在不同迎角时得到的俯仰阻尼的变化情况。图中:α为迎角,Cmq+Cm.α为俯仰阻尼。可知,与试验值相比,在迎角小于10°时,内伏牛顿流理论计算的数值偏大;而当迎角大于10°时,内伏牛顿流理论计算的数值偏小。程序计算值与试验值在计算的迎角范围内都保持了较好的一致性,由此说明了本文计算方法对于高超声速三维构型强迫运动流场模拟的结果在一定程度上也是可靠的。
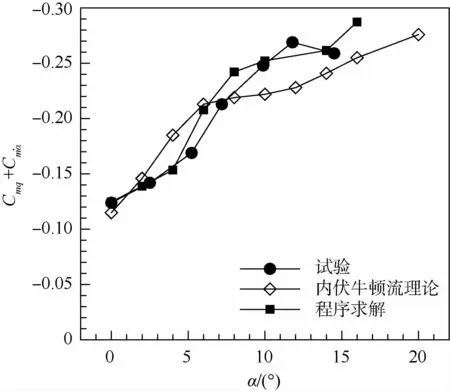
图2 俯仰阻尼随迎角的变化曲线Fig.2 Variation curves of damping in pitching motion with angle of attack
2 纵向气动导数计算和分析
气动导数是表征飞行器气动性能的重要参数,也是高速再入飞行器动态特性分析及轨道和落点位置预测时的重要参数。准确而高效地获取飞行器的气动导数,特别是动态气动导数(动导数),是飞行器设计、飞行力学和空气动力学的重要研究内容之一[17]。为了深入认识跨大气层轨道飞行器的动态特性,同时也为了厘清气动导数求解时的计算参数选择问题,本节以类X-37B的跨大气层轨道飞行器为主要研究对象,详细探讨了平均迎角、振动幅值、飞行马赫数及减缩频率等运动参数对类X-37B飞行器动态性能的影响规律。
首先介绍强迫运动俯仰阻尼计算方法。与文献[18-19]一样,俯仰运动的运动规律可以表示为
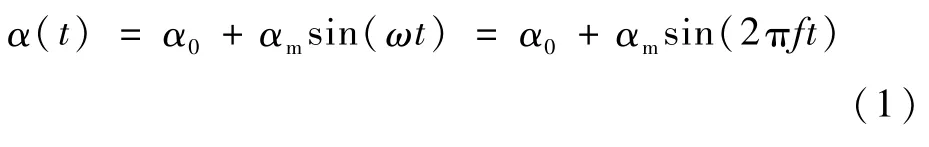
式中:α0为平衡位置处的迎角;αm为迎角的振幅;ω为简谐振动的圆频率;f为简谐振动的频率。
定义减缩频率为

式中:C为参考长度,在本文中取平均气动弦长;V∞为来流速度。
根据Etkin气动力模型[20-22],俯仰运动任一位置相对于平衡位置的非定常气动力可以表示为ΔCj =Cj-Cj0=CjαΔα+

式中:Cj为任意位置的气动力系数;Cj0为平衡位置的气动力系数;ΔCj为任意位置气动力系数和平衡位置气动力系数的差值;Cjα为任意气动力系数相对于迎角的导数;Δα和Δq分别为迎角和俯仰角速度相对于平衡位置的变化量;Cj.α和Cjq的量纲相同,都为空气动力系数对角度随时间一阶变化率的导数。
根据强迫俯仰运动时运动规律可知
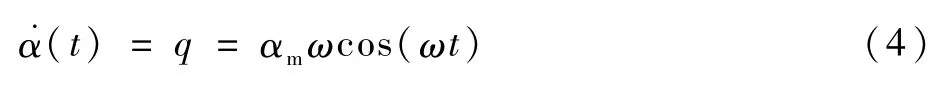
式中:q为俯仰角速度。
俯仰运动任一位置相对于平衡位置的非定常气动力可以表示为
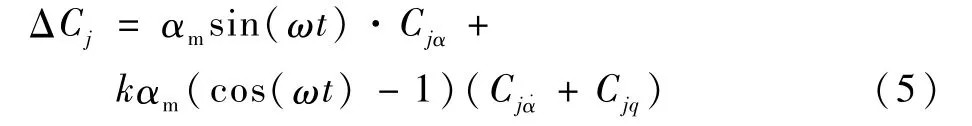
所以
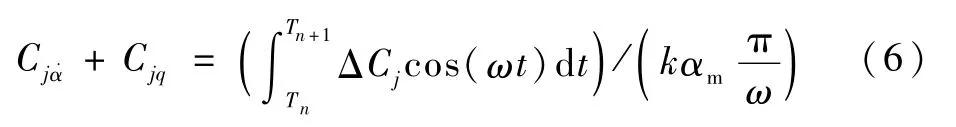
式中:Tn代表任意的时间点,Tn+1代表对应的下一个周期。
采用强迫简谐运动求解气动导数的优点是计算精度高,对于不同种类的气动导数辨识都有较好的适用性[23],缺点是存在减缩频率、振动幅值及振动初值的选择问题,如果这些值选取的不合适,求解结果误差会很大[24]。有时为了简化分析难度,传统意义上不考虑气动参数的数值随这些因素变化,但是,随着现代飞行器对机动性和操纵性要求的提高,不得不重新考虑这些因素对气动导数的影响规律。例如,振动幅值过小,数值仿真过程中气动参数的增量过小,增加了随机误差的比例,带来了精确预测动态气动参数的困难,振动幅值过大,明显增强的迟滞效应又可能造成气动参数的快速变化,从而偏离精确值。振动频率的选取也是如此,频率过低,气动增量太小,频率过高,气动增量过大,这些都会影响气动导数的精确求解。为了定量分析以上因素在气动导数,特别是动导数求解中的作用,本节以类X-37B飞行器的纵向气动导数为例,详细分析了飞行马赫数、平均迎角、振动幅值及振动频率对气动导数计算的影响效果,计算时网格变形方法采用弹簧网格方法。
图3(a)为所用飞行器的三视图,该模型与美国的跨大气层轨道飞行器X-37B类似[3-5],主要结构由机身、机翼、斜置垂直尾翼及机身后部的体襟翼构成。全机长度为7 950mm,平均气动弦长为2 838mm,机翼投影面积为9.86×106mm2,重心与机头的距离为3 356 mm。图3(b)为计算时全机不同位置的网格分布情况。可知,表面网格为三角形,空间网格为混合网格,包括附面层的三棱柱网格及其他区域的三棱锥网格。附面层第一层的高度为9.0×10-5m,增长率为1.12,一共31层。
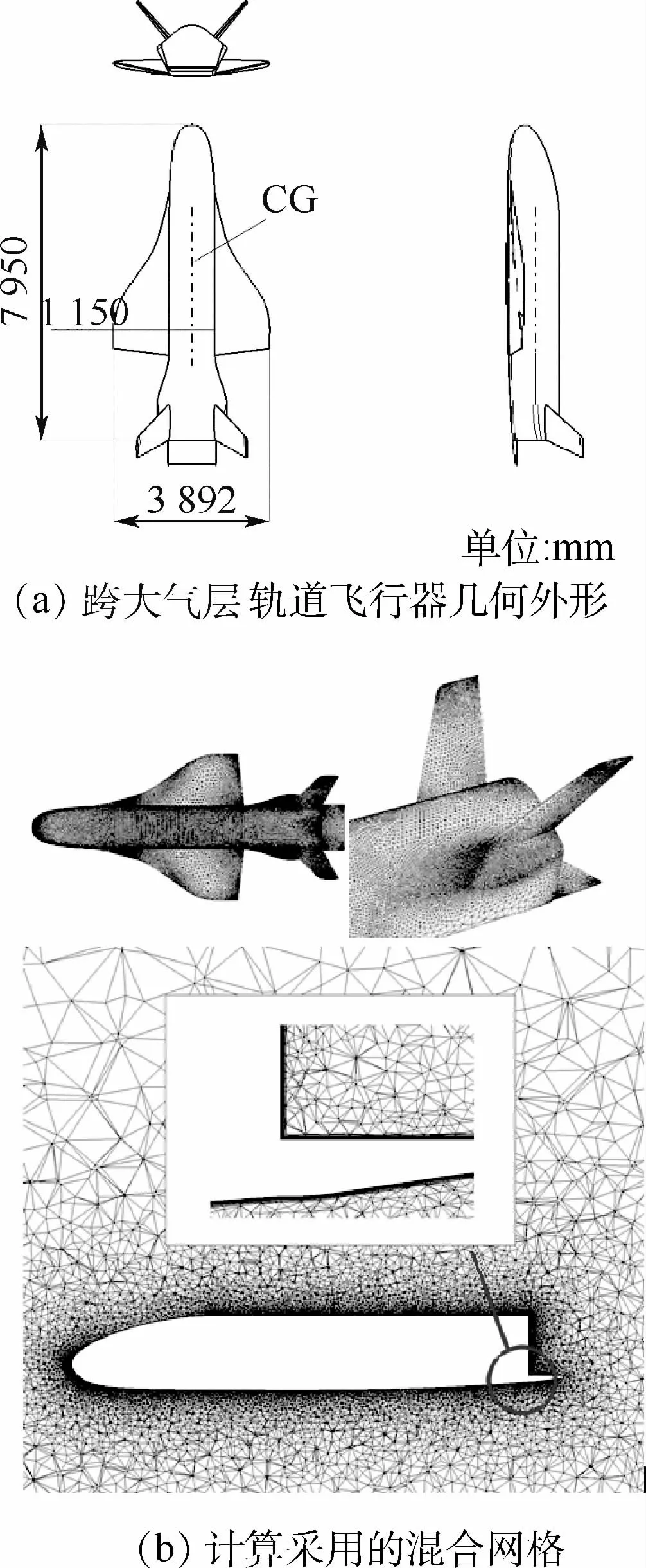
图3 跨大气层轨道飞行器的几何外形和计算采用的混合网格Fig.3 Tran-atmospheric orbiter’s geometric profile and hybrid mesh for computation
2.1 平均迎角的影响
平均迎角决定了强迫运动时的平均流场形态,由于非定常气动特性受气流时间历程的影响较大,为了探讨平均迎角对气动导数的影响规律,本节针对俯仰振动平均迎角对气动导数的影响规律展开研究。

图4 不同平均迎角时的俯仰力矩系数迟滞曲线Fig.4 Hysteresis curves of pitching moment coefficient at various average angle of attack

图5 不同平均迎角时的俯仰组合气动导数变化曲线Fig.5 Combined pitching aerodynamic derivative variation curves at various average angle of attack
图4为强迫俯仰运动在不同平均迎角时对应的俯仰力矩系数Cm迟滞曲线,图5为对应的俯仰组合气动导数的变化曲线。计算条件为:飞行高度为30 km,飞行马赫数为5.0,俯仰运动振动幅值为2°,振动频率f=10.0Hz,俯仰振动平均迎角α0=-1°~30°。由图4和图5可知,对于不同平均迎角下的俯仰力矩迟滞曲线,所有的迟滞环都是逆时针的,说明该外形在纵向是动态稳定的。不同的是,小迎角下(-1°,0°,1°,2°,3°,4°,5°,6°)迟滞曲线的外形几乎不变,也就意味着组合气动导数值基本不变,当平均迎角不小于10°(即10°,15°,20°,25°,30°)后,迟滞曲线的外形越来越尖,长轴逐渐沿着逆时针方向旋转,组合气动导数的数值逐渐增大(见图5),数值越大,代表动态稳定性越强。由于平均迎角越大,背风区的脱体涡越明显,说明对类X-37B飞行器来说,脱体涡的形成增强了纵向动稳定性。实际上,其他许多飞行器也有类似情况,甚至有的飞行器在小迎角动不稳定、大迎角动稳定,从而会出现极限环运动的情况。
2.2 振动幅值的影响
就传统上的风洞试验来说,小振幅强迫运动是获取气动导数的常用手段。随着风洞动态试验装备和测量设施的提高,近十几年来,大振幅强迫运动试验已在国内外很多风洞展开[17,23]。因为非定常气动特性受气流时间历程的影响较大,所以小振幅气动导数试验的流动与大振幅运动达到同样位置时的流动有很大差别。能否从大振幅振动动态试验中获得更多有用的气动导数信息是最近一些研究者的研究方向,由于非定常气动特性受气流时间历程的影响,为了探讨强迫俯仰运动幅值对气动导数的影响规律,本节研究俯仰振动的振动幅值对气动导数的影响规律。
计算条件为:飞行高度为30 km,飞行马赫数为5.0,俯仰运动平均迎角α0=0°,振动频率f=10.0 Hz,俯仰运动振动幅值αm=0.5°~30°。
图6为不同振动幅值时的俯仰力矩系数迟滞曲线。可知,所有的迟滞环都是逆时针的,说明不论俯仰运动的振动幅度多大,该外形在纵向总是动态稳定的。不同的是,振动幅值较小时(0.5°,1.0°,1.5°,2.0°,2.5°,3°,5°),所有的迟滞环均为椭圆形,但是振幅不小于10°(即10°,20°,30°),在俯仰运动的最高和最低位置处有一个扭曲,使得迟滞曲线也同样有一个扭曲,不再是标准的椭圆形。结合图5可知,迎角较大时,动稳定性较强,所以,在大振幅振荡运动到大迎角附近时,其俯仰力矩系数在上下行过程中的差异就有被拉大的趋势,从而导致了该扭曲。结合图7可知,虽然不同振动幅值对应的迟滞曲线外形有些许变化,但是由于在最大位置和最小位置的扭曲刚好对称,所以所有的气动导数数值变化不大,保持在-3.24左右,由此说明不同的振动幅值对类X-37B外形的纵向动态特性的影响不大。虽然大振幅运动的非定常效应更强,迟滞环也有明显的扭曲,但是大振幅运动包含小振幅运动的相关信息,所以可以准确预测出非定常气动特性。
2.3 飞行马赫数的影响
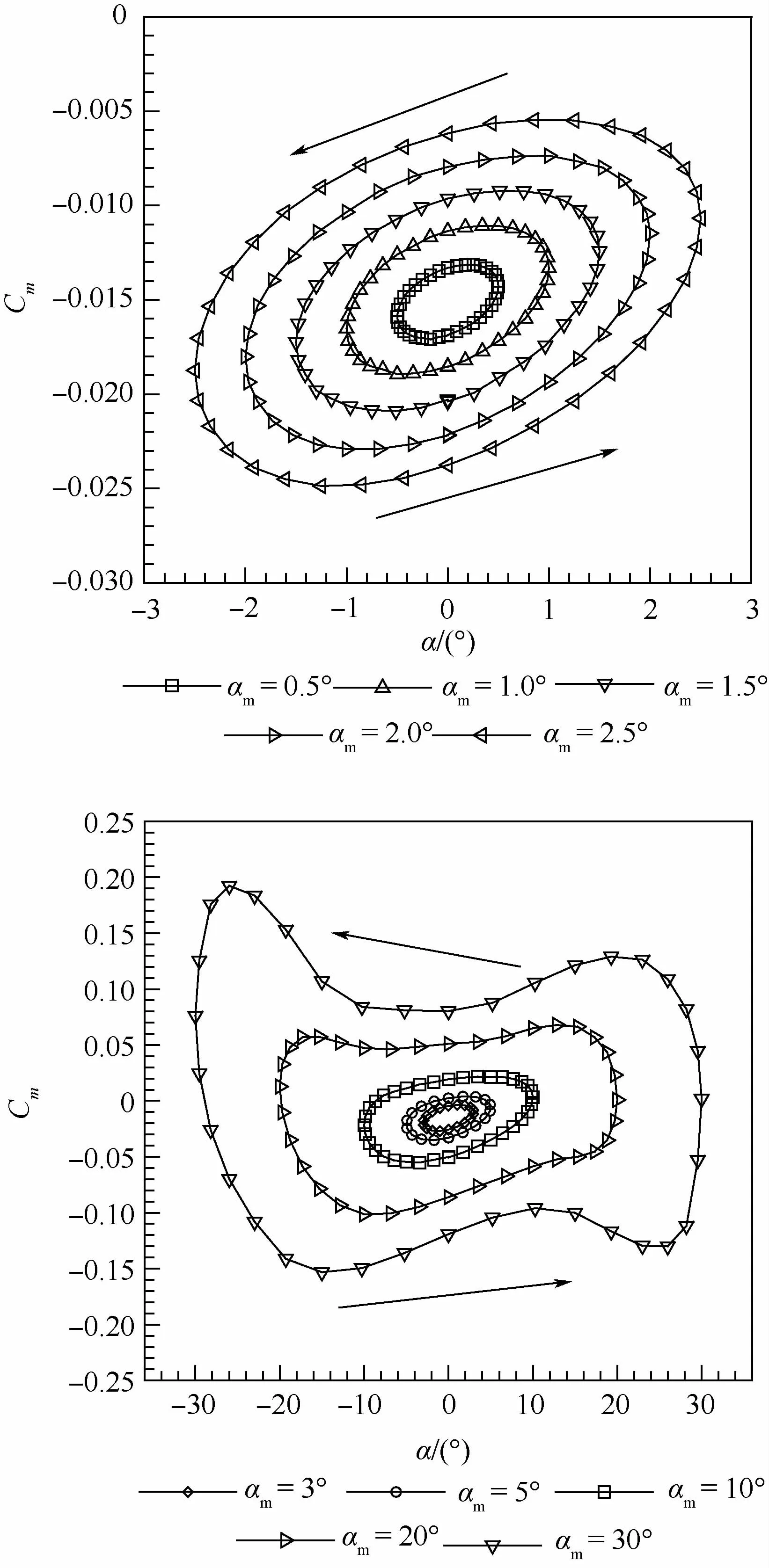
图6 不同振动幅值时的俯仰力矩系数迟滞曲线Fig.6 Hysteresis curves of pitching moment coefficient at various oscillation amplitude
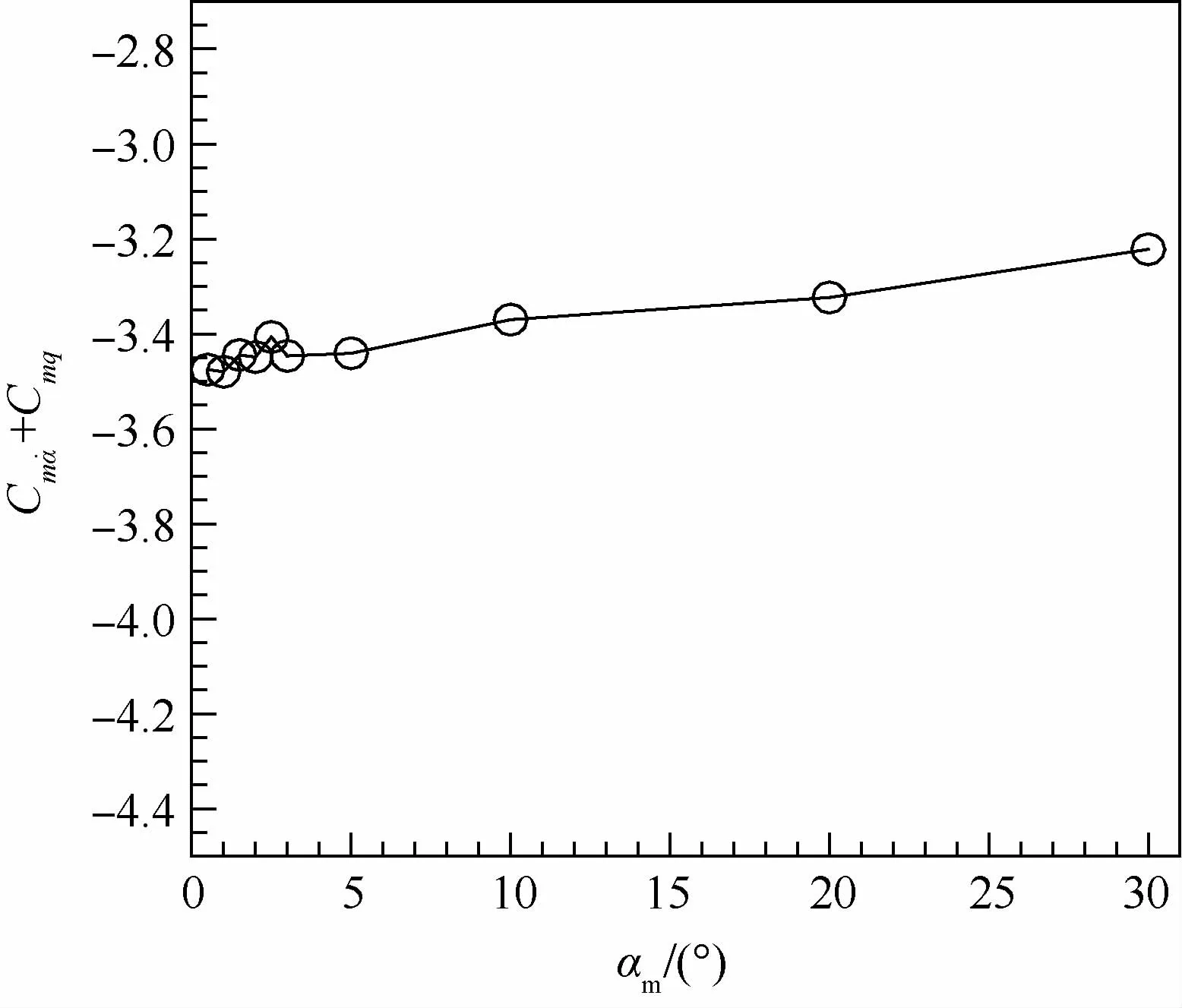
图7 不同振动幅值时的俯仰组合气动导数变化曲线Fig.7 Combined pitching aerodynamic derivative variation curves at various oscillation amplitude
飞行马赫数是气动导数的重要影响因素,飞行马赫数的变化带来了飞行速度的变化,从而直接影响飞行器表面的气动力和气动力矩,使短周期频率增加。为了定量说明飞行马赫数对类X-37B飞行器气动导数的影响规律,本节计算了不同飞行马赫数下的气动导数。计算条件为:飞行高度为30 km,俯仰运动平均迎角α0=0°,俯仰运动振动幅值αm=2.0°,振动频率f=10.0Hz,飞行马赫数变化范围为0.2~15。
图8为不同飞行马赫数下的迟滞环。可知,不同曲线的外形虽然都是逆时针的椭圆,但是飞行马赫数越小,迟滞环包围的面积越大,这是因为飞行马赫数越小,俯仰运动相对于来流来说扰动越明显,迟滞效果也越显著。结合图9可知,在亚声速范围内,随着飞行马赫数增加,气动导数数值增加,在声速附近达到最大值,这就是跨声速附近强烈非线性流场造成的跨声速凹坑现象。超声速范围内,随着飞行马赫数增大,气动导数数值减小,飞行马赫数超过10以后,气动导数的数值基本保持不变,这也与高超声速飞行马赫数无关原理相符[1-2]。
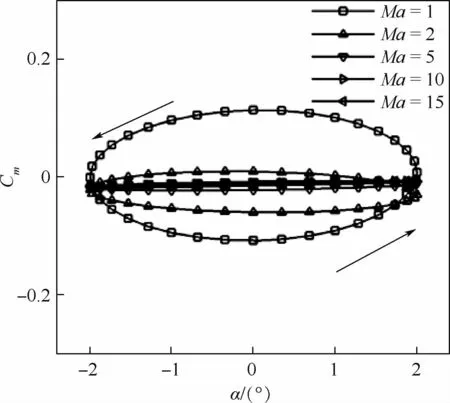
图8 不同飞行马赫数时的俯仰力矩系数迟滞曲线Fig.8 Hysteresis curves of pitching moment coefficient at various Mach number in flight
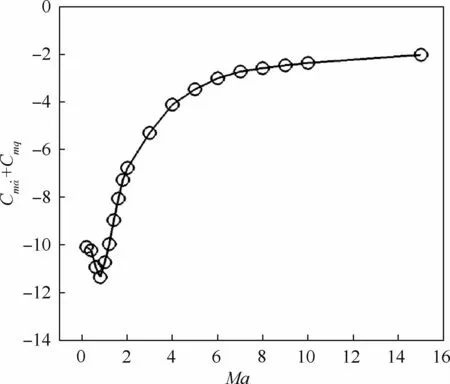
图9 不同飞行马赫数时的俯仰组合气动导数变化曲线Fig.9 Combined pitching aerodynamic derivative variation curves at various Mach number in flight
2.4 振动频率的影响
在传统的稳定性分析和飞行仿真中,频率的选取往往由经验确定,很少会考虑减缩频率对气动导数的影响[18,24]。然而对真实飞行器的实际飞行过程而言,燃油的持续消耗和油箱的安置位置将会改变飞行器的转动惯量;飞行高度的变化则会改变大气的物理特性;在突风、舵偏等扰动的持续作用下,飞行器运动的固有短周期频率会发生部分改变等,这些因素都会导致实际飞行时飞行器的固有频率不断地发生变化,因而气动导数也可能发生较大的改变,这时就必须研究气动导数随频率的变化关系,从而为稳定性分析、飞行仿真或是控制律设计提供更为准确的原始数据。为此,本节计算了不同振动频率时的气动导数。计算条件为:飞行高度为30 km,飞行马赫数为5.0,俯仰运动平均迎角α0=0°,俯仰运动振动幅值αm=2.0°,振动频率f=0.1,1,10,50,100 Hz,相应的基于平均气动弦长的减缩频率为5.91×10-4,5.91×10-3,5.91×10-2,2.96×10-1,5.91×10-1。特别要注意的是,飞行器在所有的轨道上真实飞行时的振动频率不可能到100 Hz,这里只是为了模拟某些极限的情况,探索这些极限情况下的运动特性。减缩频率在非定常计算中是一个非常重要的参数,其实际上表征了强迫振动频率的快慢,对气动导数求解影响很大,减缩频率的大小会影响气动导数的量值乃至符号。
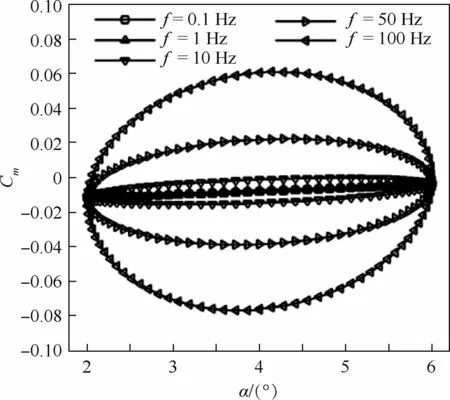
图10 不同振动频率时俯仰力矩系数迟滞曲线Fig.10 Hysteresis curves of pitching moment coefficient at various oscillation frequency
图10为不同振动频率下的迟滞曲线。可知,不同的迟滞环包围的面积不同,频率越高,迟滞环面积越大,但是处在俯仰运动的最低位置和最高位置处的力矩系数值保持不变。这是因为振动频率越高,相应的减缩频率就越大,俯仰运动非定常效应相对于来流来说扰动越明显,迟滞效果也越显著。而在俯仰运动的最低和最高位置,由于不同频率运动对应的俯仰角速度均为0,所以力矩系数的数值就相同。结合图11可知,频率变化时组合气动导数的数值变化不大。但考虑到类X-37B飞行器短周期频率较低,约为0.5 Hz,计算的较高频率的运动形式偏离了该外形的固有运动模式,预测结果可能会与真实情况不符。所以,在采用强迫运动方式分析飞行器的稳定性时,强迫运动的振荡频率不能随意给定,应该结合飞行器的典型飞行状态、典型速度分布范围、质量分布特性和静导数特性,估算给出典型振荡频率的范围,这样计算出的结果才有实际参考价值。
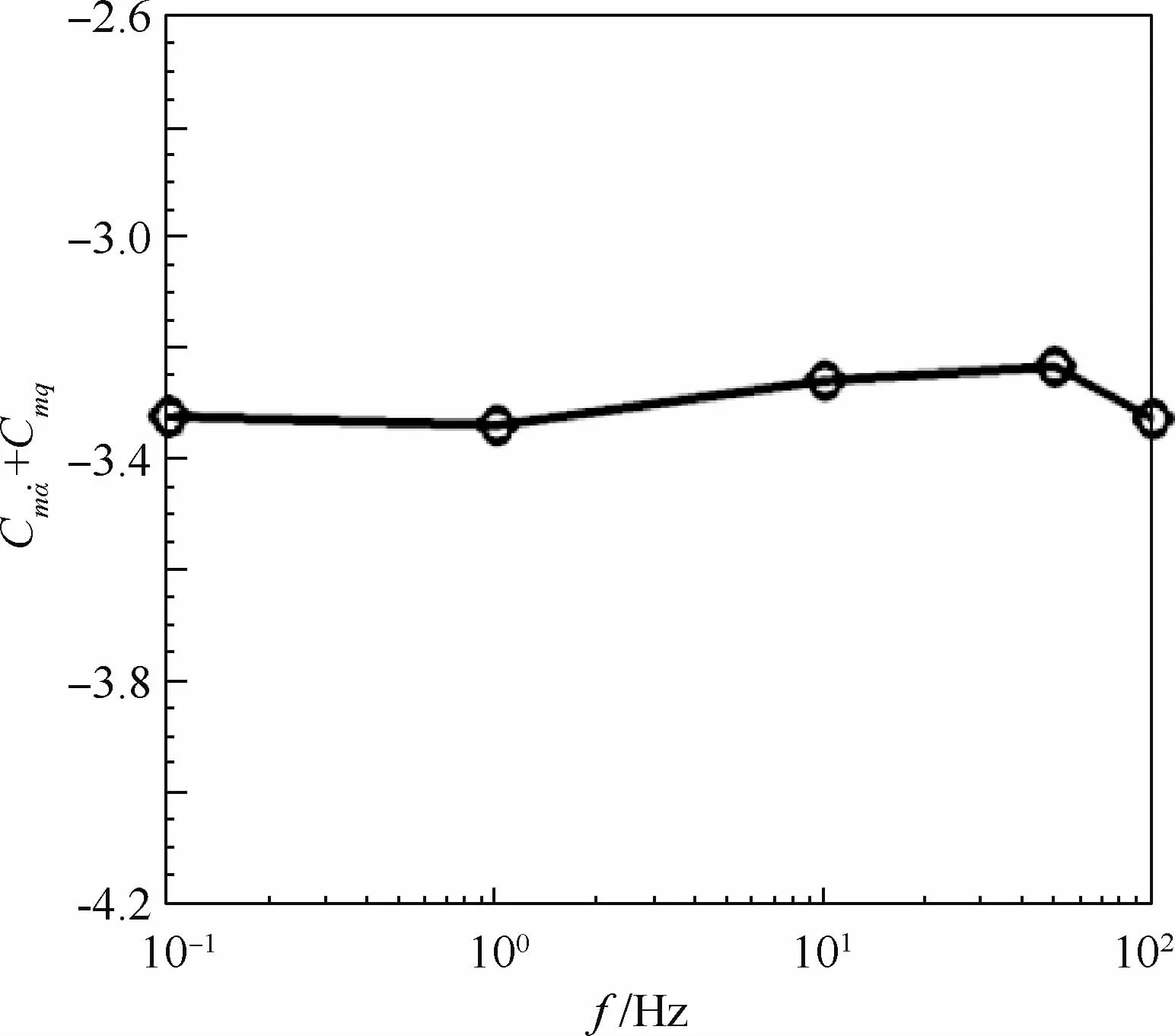
图11 不同振动频率时的俯仰组合气动导数变化曲线Fig.11 Combined dynamic derivative variation curve at various oscillation frequency
3 结 论
作为一种新型天地往返输运系统,可重复使用的跨大气层轨道飞行器的动力学相关问题很复杂。为了定量地研究这类跨大气层轨道飞行器在不同飞行条件下的动力学响应问题,同时也为了厘清计算参数选择对气动导数提取结果的影响,在Etkin气动力模型的基础上,本文详细地研究了飞行马赫数、减缩频率、振动幅值、平均迎角等因素对飞行动态稳定特性的影响规律,结果表明:
1)对于可重复使用的类X-37B飞行器来说,在计算的平均迎角范围内(-1°~30°),其纵向都是稳定的。在平均迎角小于10°时,稳定性随着迎角的增加基本保持不变,但是当平均迎角不小于10°后,随着平均迎角的继续增大,稳定性迅速增强。
2)在计算的振动幅值范围内(0.5°~30°),其纵向也都是稳定的,并且稳定性随着振幅的增加有缓慢减弱的趋势。
3)飞行马赫数对纵向稳定性的影响比较显著,在计算的飞行马赫数范围内(0.2~15),其纵向也都是稳定的。当飞行马赫数小于1时,稳定性随着飞行马赫数的增加迅速增强,当飞行马赫数继续增大时,稳定性又开始减弱,当飞行马赫数超过10以后,稳定性基本保持不变。
4)强迫运动的振动频率也是影响飞行器气动导数求解的关键因素,因为振动频率与代表流动非定常程度的减缩频率是一一对应的。本文计算的振动频率范围为0.1~100 Hz,对应的减缩频率范围为5.91×10-4~5.91×10-1。计算结果表明,对类X-37B飞行器来说,稳定性参数与强迫运动频率的大小没有明显关系。但是,需要注意的是,在采用强迫运动方式分析飞行器的稳定性时,强迫运动的振荡频率不能随意给定,应该结合飞行器的运动状态、质量分布规律和静导数特性,估算出典型振荡频率的范围,这样计算出的结果才有实际参考价值。

