一种基于等区域划分的RFID防碰撞算法

胡黄水, 张 国, 王宏志, 赵宏伟, 王出航

(1.长春工业大学 计算机科学与工程学院, 长春 130012; 2.吉林建筑科技学院 计算机科学与工程学院, 长春 130114;3.吉林大学 计算机科学与技术学院, 长春 130012; 4.长春师范大学 计算机科学与技术学院, 长春 130032)

随着物联网[1-6]的迅速发展, 射频识别(radio frequency identification, RFID)技术作为物联网感知层的重要组成部分之一, 在各领域得到广泛应用[7].当多个阅读器或标签同时存在于RFID系统中时, 无线电信号之间会相互干扰, 导致标签与阅读器之间产生应答错误, 出现碰撞问题[8-10].包括同一标签和多个阅读器之间产生的阅读器碰撞、 多个标签和同一阅读器之间产生的标签碰撞[11-13].由于在实际应用场景中, RFID系统对多标签碰撞问题处理能力较弱, 导致系统吞吐率较低[14].

基于时分多路类的随机性算法和确定性算法目前已成为主流的多标签RFID防碰撞算法[15], 其中随机性算法以Aloha类算法为主, 确定性算法则主要源于树形搜索算法.相比于Aloha类算法, 树形搜索算法虽能保证标签识别率, 但增长了系统识别周期, 提高了系统设计的复杂性.基本的Aloha类算法[16-17]包括纯Aloha(pure aloha, PA)算法、 时隙Aloha(slotted Aloha, SA)算法、 帧时隙Aloha(framed slotted Aloha, FSA)算法和动态帧时隙Aloha(dynamic framed slotted Aloha, DFSA)算法[18].FSA算法[19-20]将一帧分成多个时隙, 并规定了每帧中标签仅响应一次，当标签发生碰撞后, 标签延迟至下一帧继续传输数据，但由于FSA算法中帧长固定, 导致系统识别稳定性较差; GDFSA算法[21]将动态调整时隙数原则和标签分组方法相结合改进RFID防碰撞算法, 但该算法的识别效率并未得到有效提高；文献[22]提出了一种基于优先级的RFID防碰撞算法, 设计了标签的优先级分组信息并对标签的响应次序进行了调整, 但该算法并未对大规模标签应用场景进行仿真验证; 文献[23]提出了一种基于距离预测分组的Aloha算法, 根据标签分布距离进行分组, 但该算法只优化了DFSA算法的使用范围, 并未对标签的识别部分做出实质修改.

针对现有算法存在的各种不足, 本文提出一种基于等区域划分的RFID防碰撞(an RFID anti-collision algorithm based on equal area division, BEAD)算法, 通过将阅读器识别范围内的标签进行均等区域划分建立一种新型的分组结构, 根据标签数量多少将阅读器识别范围划分为1～N个组.为进一步优化系统吞吐率, 将改进的Aloha算法在每组中分别使用, 通过对DFSAC-Ⅱ算法进行改进得到动态预测权值后, 使每轮剩余标签数目的估计更准确, 在此基础上优化时隙数进而达到标签高效快速识别的目的.仿真结果表明, 在大规模标签应用场景中, BEAD算法能有效提高系统吞吐率并改善标签增多导致系统稳定性差的问题, 减少了通信过程中的时隙数.

1 算法设计

本文首先确定阅读器最大功率识别范围, 对识别范围内的标签进行均等区域分组, 限制每次识别的标签数目, 并对已有的标签估计算法进行优化, 在分析标签数和时隙数的基础上, 进行最优时隙数调整, 使每次估计出的标签数目与时隙数相对应, 进而提高系统吞吐率.

1.1 基本定义

BEAD算法规定将一帧划分为T个时隙, 即时隙数为T, 同时规定阅读器识别范围内的待识别标签总数为m.由于标签对时隙进行选择的过程是互不相关独立选择的过程, 与其他标签无关, 故可将标签与时隙的匹配识别过程视为一个多重Bernoulli试验, 将其转化为一个二项分布的数学问题, 概率表示如下：

(1)

其中k∈[0,m]且k取整.当k=1时, 根据式(1)可得成功时隙的概率[12], 即一个时隙只有一个标签选择的概率为

(2)

同理可得当k=0时空闲时隙的概率, 即一个时隙无任何标签选择的概率为

(3)

当k≥2时, 碰撞时隙的概率, 即一个时隙有多个标签同时选择的概率可通过概率总和为1的原则表示为

Pe=P(X≥2)=1-P(X=1)-P(X=0).

(4)

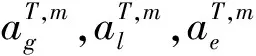
规定系统吞吐率为SRFID, 即一帧内阅读器成功识别标签与总时隙数的比值, 公式为

(8)

对式(8)求导可得

(9)

对式(9)求极值可得时隙数与标签数的函数关系为

(10)

式(10)表明当系统可分配的时隙数约等于标签数, 且标签数远大于1时, 系统吞吐率达到极值.此外, 如果所有时隙均为空闲时隙, 或所有响应的标签均由于碰撞而识别失败, 则吞吐率变为最小值0; 在一次识别周期内, 如果所有标签都被成功识别, 则吞吐率达到最大值1.

1.2 等区域分组

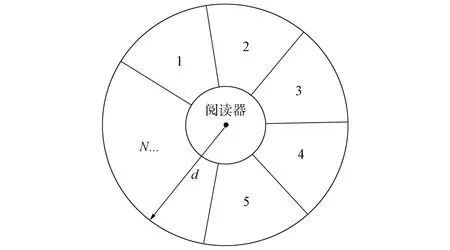
图1 等区域分组示意图

由于标签以阅读器为中心随机分布, 且RFID系统具有标签数目越小, 系统识别效率越高的特性, 故根据等区域划分的思想将阅读器识别范围内的所有标签进行分组, 即以阅读器为中心进行扇形分组, 通过将每组标签分开识别达到提高系统识别效率的目的.等区域分组结构示意图如图1所示.

在无线通信系统中, 信道是随时间变化的, 故需考虑标签与阅读器之间距离导致的路径损耗.在无线信道中, 平均接收功率(dBm)与发射机和接收机间的距离的对数成反比, 故设系统的平均接收功率为

(11)

其中:d为阅读器识别范围；λ为路径衰落指数, 即随着距离增长路径损耗的速度, 一般取值为2～5；d0为近地参考距离.

1.3 标签数目估计

目前RFID防碰撞算法的系统吞吐率主要依赖于标签数与时隙数, 当未识别标签数远大于系统分配时隙数时, 随着碰撞时隙数增多, 系统吞吐率会变低；当未识别标签数与系统分配时隙数越接近, 系统吞吐率会达到最大.所以, 为了优化系统吞吐率, 本文在分析现有标签估计算法的基础上对其进行了优化.在经典标签估计算法中, DFSAC-Ⅱ主要用于静态标签估计场景, 而Vogt标签估计算法则更适用于动态标签估计场景, 但由于Vogt算法计算复杂度过高, 故本文主要在DFSAC-Ⅱ标签估计算法的基础上进行优化.

设成功时隙数、 空闲时隙数和碰撞时隙数分别为Tg,Tl,Te.假设经过n轮查询, 待识别标签总数与碰撞时隙数具有线性函数关系, 则第(n+1)轮标签数目预测公式为

mpredict(n+1)=ξ·Te(n).

(12)

相应地, 当第(n+1)轮标签数目估计开始后, 采用DFSAC-Ⅱ算法计算当前帧的待估计标签数, 对第n轮的预测结果进行调整：

madjust(n+1)=2.392 2·Te(n+1).

(13)

则用第n轮的预测结果与第(n+1)轮的调整结果相减可得理论误差值为

ε=mpredict(n+1)-madjust(n+1)=ξTe(n)-2.392 2Te(n+1).

(14)

为了得到最小误差, 通过对理论误差值的平方关于ξ求导得到极小值为

(15)

令式(15)为0, 解得标签估计的动态预测权值为

(16)

由于算法在实际执行过程中无法做到提前得到下一轮的碰撞时隙数, 所以将公式进行相应地修改, 通过将本轮的时隙数及上一轮的时隙数代入上述公式可得动态预测权值ξ为

(17)

将ξ代入式(12), 可得下一轮预测标签数目为

(18)

1.4 最优时隙数调整

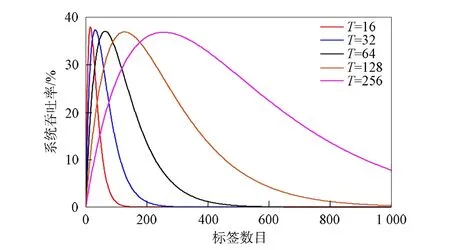
图2 不同固定时隙数下的吞吐率

由于标签成本受硬件条件限制, 时隙数不能随意分配, 所以需要在标签估计的基础上对标签进行最优分组, 并在此基础上动态调整时隙数进一步提高系统吞吐率.

通常情况下, RFID系统中时隙数取值一般是关于2x的函数, 且由于受硬件成本限制, 时隙数最大取28, 超过将失去实际应用价值, 故时隙数的取值为{22,23,24,25,26,27,28}数集.图2为不同固定时隙数下, 标签数目增加对系统吞吐率变化的影响趋势.由图2可见, 两相邻时隙数的交点为标签数目影响系统吞吐率变化的临界点, 将相邻两个固定时隙数代入式(8)可得时隙数对应的标签数量, 进一步求得分组临界点.相邻两时隙数的吞吐率关系可表示为

(19)

从T=22开始将整个数集逐次代入式(19)可得

(20)

例如, 当T=22时,m≈5.5, 取m=5, 则5为当时隙数为22时的最大标签数.分组结果列于表1.

表1 时隙与分组数的对应关系

1.5 算法流程

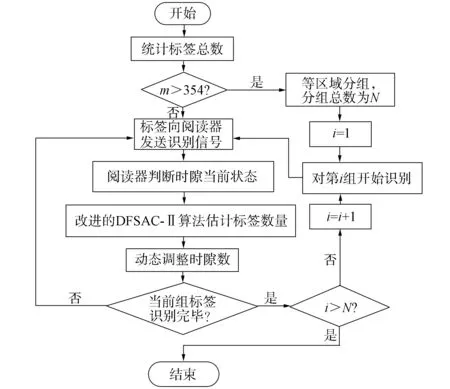
图3 BEAD算法流程

图3为BEAD算法流程, 算法识别过程如下：

步骤1)在识别开始前, 统计标签总数, 当标签总数大于354时, 在阅读器识别功率覆盖范围内进行等区域分组, 通过将阅读器识别范围划分为1～N个面积相等的扇形进而达到对标签分组的目的;

步骤2)从第1组开始, 设定初始时隙数, 组内标签初始化, 随机选择一个时隙并向阅读器发送信息;

步骤3)系统根据本轮已获得的标签选择信息判断每帧的时隙状态, 并根据时隙的选择情况采用改进的DFSAC-Ⅱ算法估计当前组内剩余标签数;

步骤4)通过已获得的本轮标签数信息, 系统对时隙数做出最优调整并分配下一轮时隙数;

步骤5)阅读器对成功识别的标签发送休眠命令, 使其退出本轮查询过程; 碰撞标签延迟至下一帧重新开始识别过程, 直到本组标签全部休眠为止;

步骤6)本组识别完毕后, 组数加1, 转步骤2), 开始新一轮的识别过程, 并采用相同方式进行识别, 直到系统识别范围内所有组的标签识别完成, 算法结束.

2 算法性能分析

为了分析BEAD算法的有效性, 本文选择MATLAB软件作为仿真平台, 通过实验分析算法的可靠性.将BEAD算法与FSA_256算法和DFSA算法进行性能比较, 采用吞吐率和标签识别过程中系统消耗的总时隙数作为评价性能优劣的评价指标.仿真实验中, 假设标签分布均匀, 系统标签数目设为1 500, BEAD算法、 FSA_256算法及DFSA算法初始时隙数均设为256.为了增加实验结果的权威性, 令标签数从50开始, 直到标签总数增加到1 500, 记录每次变化的仿真结果, 并对每次仿真结果取平均值.

2.1 系统分组数分析

等区域分组结构分组方法表示为

(21)

其中:N为分组数;m为标签总数; down表示向下取整.本文实验中, 分组数不断变化, 当标签总数为354时,N=1；当标签总数达最大值1 500时,N=4.

2.2 系统传输总时隙分析

图4为不同标签数量下系统消耗总时隙数增加情况.由图4可见, 当标签数为850时, FSA_256算法和DFSA算法所消耗的时隙总数随着标签数量的增加呈指数增长, 这是由于256的时隙数过短, 引起碰撞次数增多所致, 当标签总数达1 500时, FSA_256算法和DFSA算法所消耗的时隙总数分别达21 248和20 520.而BEAD算法性能明显优于FSA_256算法和DFSA算法, 所需时隙数增长缓慢, 呈线性增长趋势, 当标签数为1 500时, 所需总时隙数为4 935, 与FSA_256算法相比降低了76.77%, 与DFSA算法相比降低了75.96%.这是由于BEAD算法根据时隙数与标签数分组关系对标签总数进行了合理的分组, 使每组标签最大识别总数不超过354, 从而有效减少了碰撞时隙的增加, 节省了大规模标签应用场景下的RFID系统识别时间.

2.3 系统吞吐率分析

图5为不同标签数量下系统吞吐率的变化情况.由图5可见, FSA_256算法的系统吞吐率最小, 在标签数约为650时, 吞吐率达最大值28.21%.DFSA算法的系统吞吐率得到了相应提高, 在标签数约为300时, 最大吞吐率达37.88%.BEAD算法相比于FSA_256算法和DFSA算法均有不同程度的改善.在标签数约为400时, 最大吞吐率达43.95%.这是由于本文采用的动态权值估计法同时结合了当前帧的碰撞时隙数与上一帧的碰撞时隙数, 在每轮时隙数更新后动态改变预测权值, 使标签数估计更合理.当系统待识别标签数量超过850时, FSA_256算法和DFSA算法的系统性能相近, 并逐渐降低, 而BEAD算法的系统吞吐率仍稳定在30%以上.

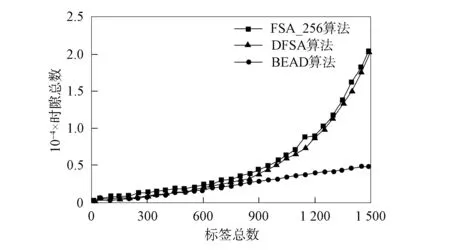
图4 总时隙数比较

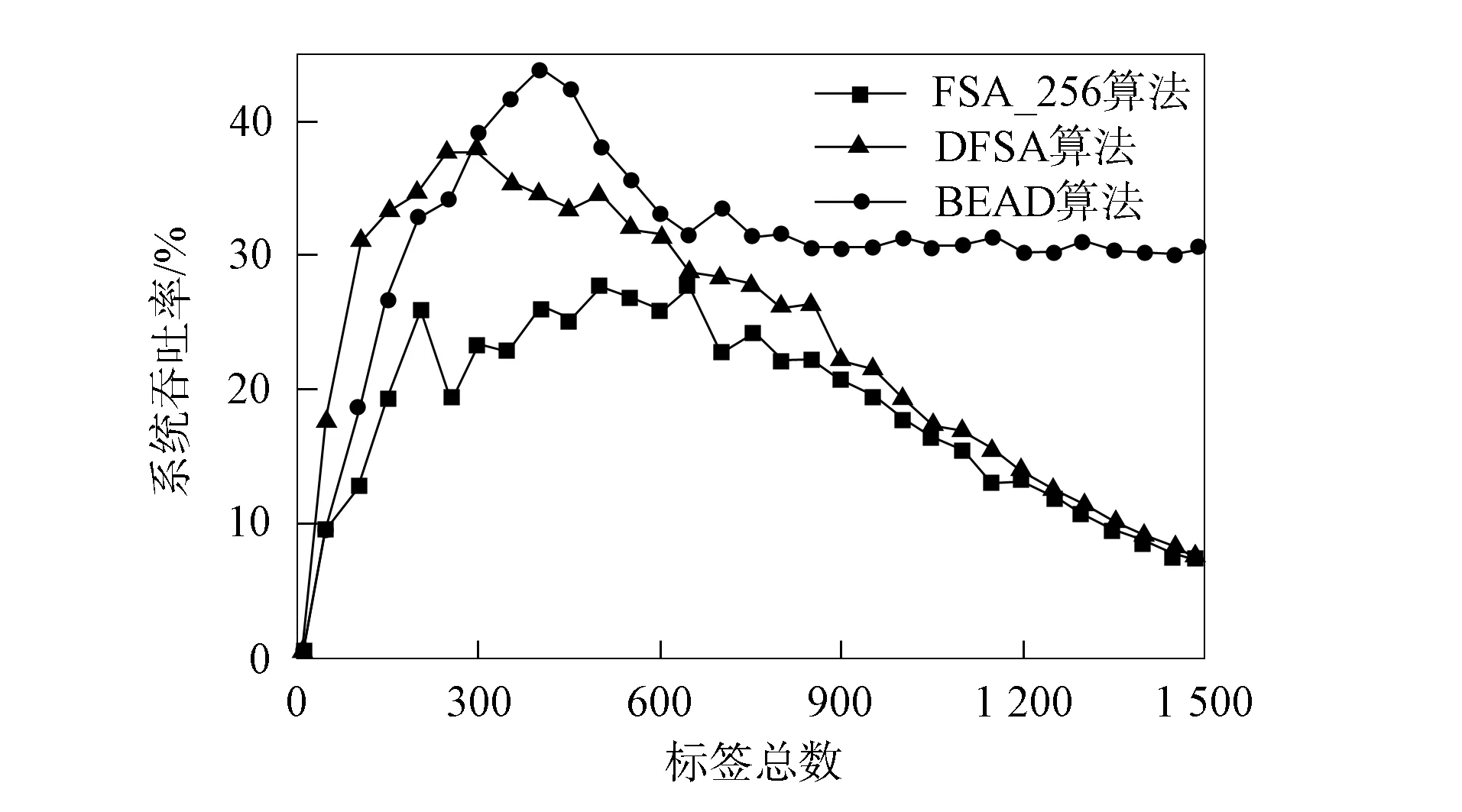
图5 吞吐率比较

综上所述, 针对标签数量过多引起的RFID识别系统时隙碰撞率过高等问题, 本文提出了一种基于等区域划分的RFID防碰撞(BEAD)算法.通过分析不同时隙数与标签数对应关系下的最大吞吐率, 对标签进行分组识别，并对组内标签进行动态估计以及最优时隙数调整提高系统的时隙利用率.仿真结果表明, 在大规模标签应用场景下, 与FSA_256算法和DFSA算法相比, BEAD算法的系统吞吐率较高, 通信消耗的总时隙更少, 具有良好的稳定性, 对物联网感知层技术的发展有一定的借鉴意义.