具有迁移性质的Ross-Macdonald系统的格子Boltzmann方法

李 婷, 闫广武

(1.吉林化工学院 理学院, 吉林 吉林 132022; 2.吉林大学 数学学院, 长春 130012)

0 引 言

格子Boltzmann方法(LBM)因其算法简单、 并行计算、 复杂边界条件易处理等优点而得到广泛应用, 目前已成为一种有效的求解各类非线性偏微分方程的数值方法, 如反应扩散方程[1]、 Maxwell方程组[2]、 热波方程[3]、 Wave-Like方程[4]、 Ginzburg-Landau方程[5]等.文献[1]给出了用于反应扩散方程的LBM模型, 得到了与经典方法相近的数值结果.本文考虑具有迁移性质的Ross-Macdonald方程的格子Boltzmann模型, 并将LBM数值结果与经典中心差分格式的结果[6]进行比较, 结果表明, 两种方法结果相符.

具有迁移的Ross-Macdonald方程描述了疟疾病疟蚊的演化规律[7-9], 其偏微分方程的初边值问题[10-11]为

(1)

其中:Ω⊂n表示疟疾病疟蚊区域;u为感染疟疾病病人所占人口的密度,v为疟蚊占蚊子种群数的密度,u0,v0分别是u,v的初值;α为蚊子的叮咬率,β为蚊子叮咬后的发病率,μ表示蚊子的死亡率,γ为疟疾病病人恢复健康率,α,β,μ,γ均为正的常数; Δ为二维Laplace算子.由于Δ的系数为1, 因此该方程扩散性质较弱, 更具有迁移性质.

1 具有迁移过程的Ross-Macdonald系统的格子Boltzmann模型

选择二维5-bit网格, 分布函数fα(x,t)表示在位置x处、t时刻, 具有速度eα(α=0,1,…,b)的粒子出现的概率, 其中α=4表示静止粒子, 在二维空间中b=4, 粒子速度为

e0=(c,0),e1=(0,c),e2=(-c,0),e3=(0,-c),e4=(0,0),

式中c表示速率.定义宏观量

(2)

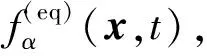
(3)

平衡态分布函数(3)满足格子Boltzmann方程:

(4)

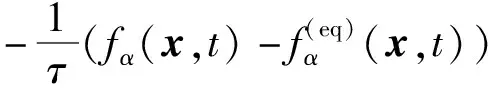
引入Knudsen数ε作为数值模拟的时间步长和Chapman-Enskog展开的小参数, 在该尺度上方程(4)可写为

(5)

假设方程(5)中

Sα=ε2Φα(t).

(6)

运用Chapman-Enskog展开和多尺度技术, 对方程(6)进行Taylor展开, 保留余项到O(ε2)的精度, 可利用不同时间尺度上的系列格子Boltzmann方程[12]:

(7)

(8)

其中:

将式(7)+式(8)×ε并对α求和, 同时假设

(9)

得宏观具有迁移的Ross-Macdonald方程为

(10)

其中

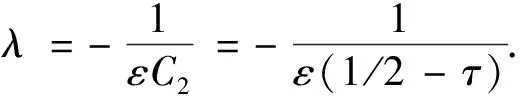
在推导方程(10)的过程中结合方程(1)可得

(11)

结合方程(3),(9),(11)易得平衡态分布函数为

其中D表示空间维数.

2 数值算例

为了验证模型效果, 在数值模拟区域内分别通过取不同的初始条件进行数值模拟, 下面以方程(1)中u的数值解为例,v的数值解模拟情况同理.

例1初始条件: 在数值模拟区域内

(12)

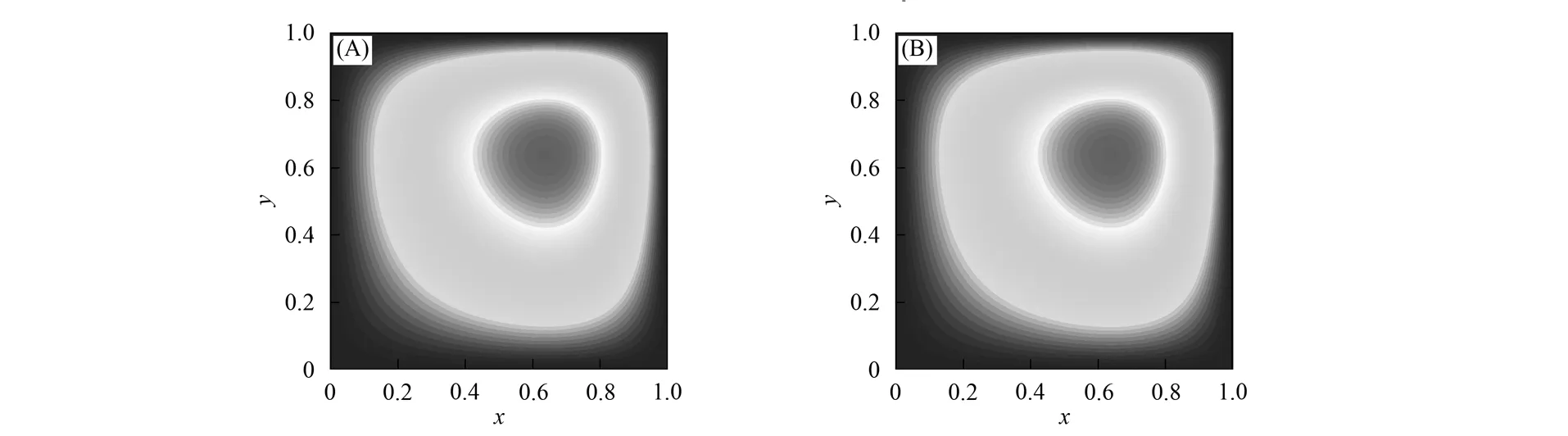
图1 例1的LBM数值解(A)及有限差分法数值解(B)

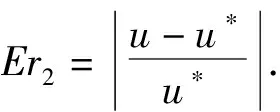
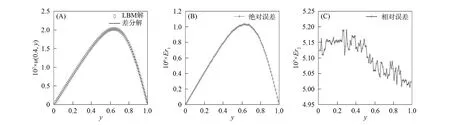
图2 当x=0.4, t=0.024时, LBM数值解和有限差分法数值解的比较(A)、 绝对误差曲线(B)及相对误差曲线(C)

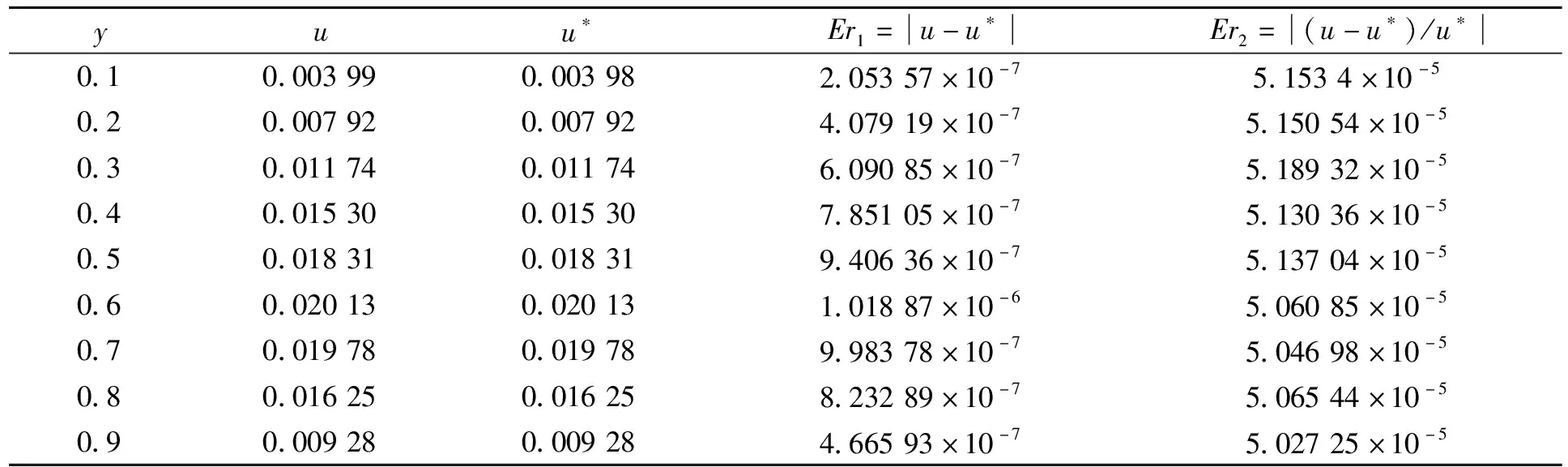
表1 当x=0.4, t=0.024时观测数据对比

图3(A)为观测点(0.65,0.55)在t≤0.024时的LBM数值解u和有限差分法数值解u*的比较结果；图3(B)为两种结果的绝对误差Er3=|u-u*|；图3(C)为两种结果的相对误差Er4=|(u-u*)/u*|.

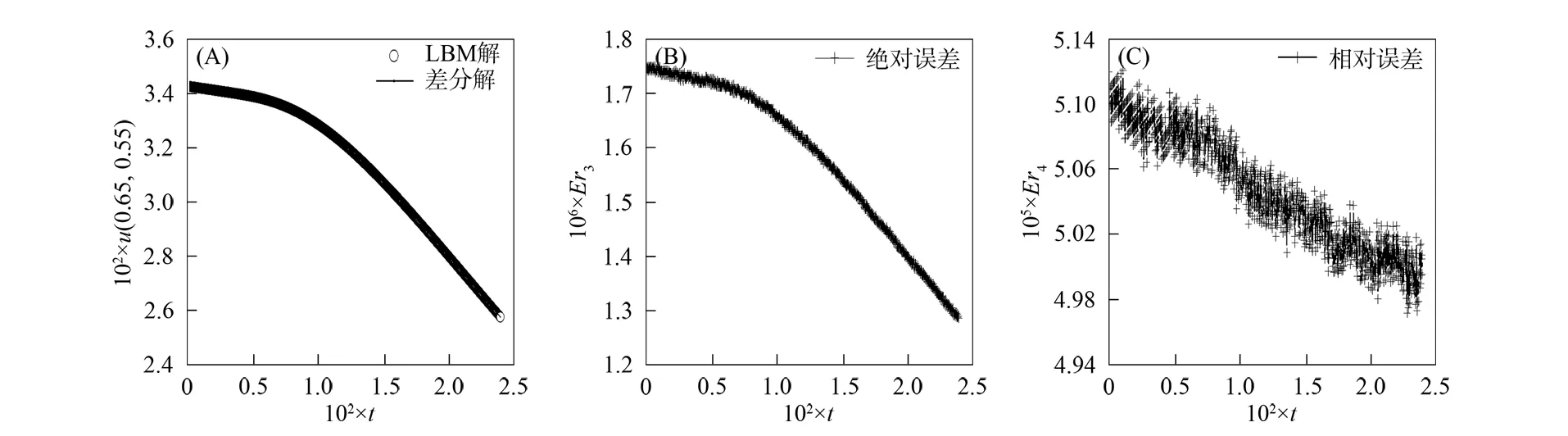
图3 当t≤0.024时, LBM数值解和有限差分法数值解的比较(A)、 绝对误差曲线(B)及相对误差曲线(C)

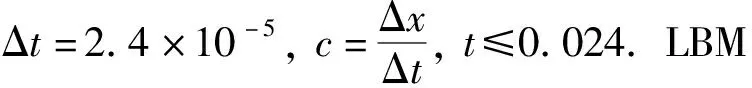
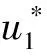
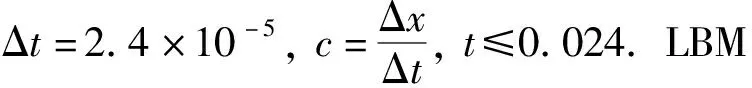
图4 例2的LBM数值解(A)及有限差分法数值解(B)

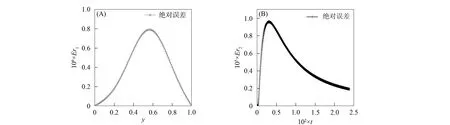
图5 LBM数值解(A)和有限差分法(B)的绝对误差曲线

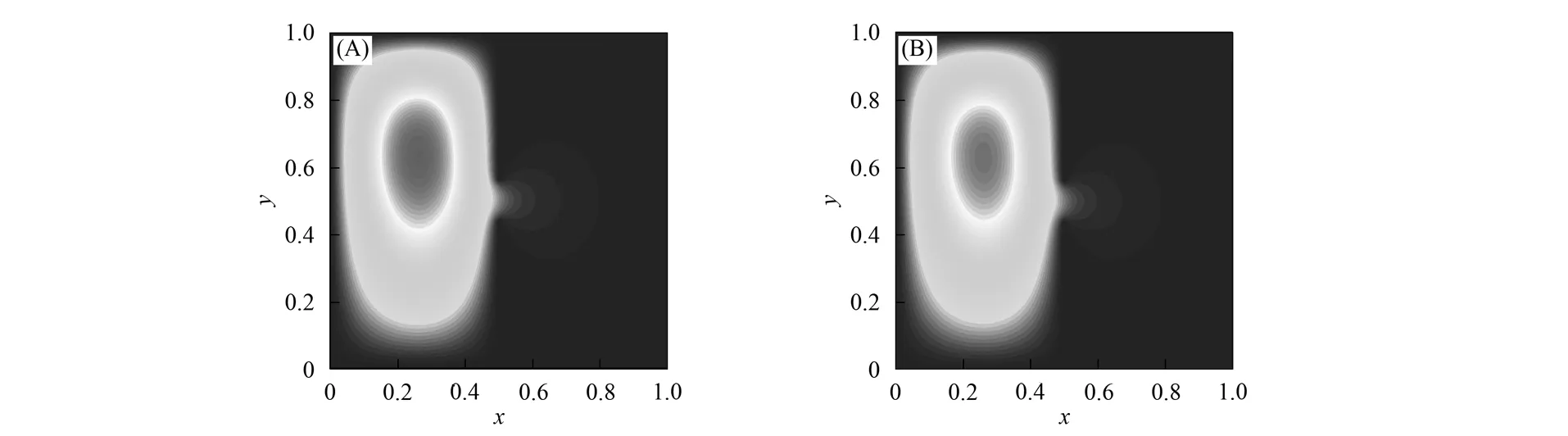
图6 例3的LBM数值解(A)及有限差分法数值解(B)

综上可见, 本文提出了一个应用于具有迁移性质的Ross-Macdonald系统的格子Boltzmann 模型, 通过3个实例的数值模拟, 并且与有限差分法数值解进行对比, 结果表明, LBM是可以用于模拟具有迁移的Ross-Macdonald系统的一种数值方法.

在完成本文过程中多次与吉林大学数学学院王博宇、 陈建华进行讨论, 受益匪浅, 深表感谢.