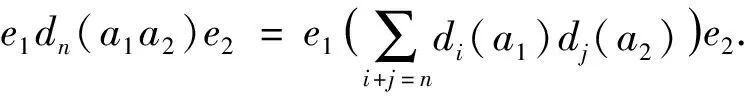三角代数上一类局部非线性三重高阶可导映射

费秀海, 戴 磊

(1.滇西科技师范学院 数理学院, 云南 临沧 677099; 2.渭南师范学院 数学与统计学院, 陕西 渭南 714099)

1 预备知识

设A是交换环R上的代数,是非负整数集,D={dn}n∈是A上的一列线性映射(其中d0=idA是恒等映射),Ω={x∈A:x2=0}.若对任意的x,y∈A,n∈, 有则称D是高阶导子; 若对任意的x,y,z∈A,n∈, 有

(1)

则称D是三重高阶导子; 进一步, 若D={dn}n∈无可加性假设, 对任意的x,y,z∈U,n∈且xyz∈Ω, 有式(1), 则称D是A上的一个局部非线性三重高阶可导映射.

近年来，算子代数上各类映射的研究已成为算子代数研究领域中的热点问题, 如: 文献[1-3]分别研究了套代数、 三角代数、 广义矩阵代数上的全可导点、 Jordan高阶全可导点及交换零点Jordan可导映射; 文献[4-5]刻画了素环和B(X )上的非线性Lie可导映射; 文献[6-10]研究了三角代数上的Lie导子、 非线性Lie(高阶Lie)可导映射、 非线性广义Lie可导映射; 文献[11-12]把非线性和局部相结合研究了上三角矩阵代数和全矩阵代数上的非线性零点可导映射；特别地, 文献[13]研究了三角代数上的局部非线性三重可导映射.基于上述研究, 本文主要刻画三角代数上的局部非线性三重高阶可导映射.

设A和B是定义在单位交换环R上含有单位元的代数, M是含有单位元的(A,B)-双边忠实模, 即M既是A的左模又是B的右模.则称R-代数

在矩阵通常的加法与乘法运算下是一个三角代数.设1A和1B分别是代数A和B中的单位元, 1 是三角代数U中的单位元, 用e1和e2分别表示:

显然, 三角代数U可被分解为

U=e1Ue1+e1Ue2+e2Ue2=A+M+B.

从而对任意的x∈U, 可以将x分解成x=a+m+b, 其中:a∈A;m∈M;b∈B.

2 主要结果

定理1设U是一个2-无挠的三角代数,Ω={x∈U:x2=0},D={dn}n∈是U上一列映射(无可加性假设).若对任意的n∈,x,y,z∈U且xyz∈Ω, 式(1)成立, 则D是一个可加的高阶导子.

对定理1的证明主要用数学归纳法, 在证明过程中总假设U是一个2-无挠的三角代数,是非负整数集,+是正整数集,Ω={x∈U:x2=0},D={dn}n∈是U上的一个局部非线性三重高阶可导映射.由文献[13]中定理2.1知, 当n=1时,d1在U上是一个可加的导子, 从而d1有如下性质(P1):

下面假设当1≤l

证明D={dn}n∈在U上是一个可加的高阶导子.

引理1对任意n∈+, 有dn(0)=0,dn(M)⊆M,dn(e1)和dn(e2)∈M且dn(e1)+dn(e2)=0.

证明: 在式(1)中令x=y=z=0, 则xyz=0∈Ω, 从而由归纳假设性质(P2), 有

对任意的m∈M, 在式(1)中令x=y=e1,z=m, 由于e1e1m=m∈Ω, 从而由归纳假设性质(P2), 有

从而有dn(m)=2e1dn(e1)e1m+e1dn(m).类似地, 可得dn(m)=2me2dn(e2)e2+dn(m)e2.于是可得e1dn(m)e1=e2dn(m)e2=0, 从而dn(M)⊆M, 进而由U的2-无挠性及M的忠实性, 可得

e1dn(e1)e1=e2dn(e2)e2=0.

(2)

在式(1)中令x=z=e1,y=e2, 由于xyz=0∈Ω, 从而由归纳假设性质(P2), 有

类似地, 在式(1)中令x=z=e2,y=e1, 可得2e2dn(e1)e2=0, 从而由U是2-无挠性, 有

e2dn(e1)e2=e1dn(e2)e1=0.

(3)

因此, 由式(2),(3)可得dn(e1),dn(e2)∈M.在式(1)中令x=y=e1,z=e2, 由于xyz=0∈Ω, 从而由归纳假设性质(P2), 有

于是可得e1dn(e1)e2+e1dn(e2)e2=0.证毕.

引理2对任意n∈+, 有dn(A )⊆A+M,dn(B)⊆M+ B.

证明: 对任意的a∈A, 在式(1)中令x=z=e2,y=a, 因为xyz=0∈Ω, 从而由归纳假设性质(P2), 可得

进而有dn(A )⊆A+M.类似地, 可证dn(B)⊆M+B.证毕.

引理3对任意n∈,a∈A,m∈M,b∈B, 有:

证明: 1)对任意在b∈B, 在式(1)中令x=y=e1,z=b, 则xyz=0∈Ω, 从而由归纳假设性质(P2)及引理1, 有

因此

(4)

类似地, 可得

(5)

对任意a∈A,b∈B, 在式(1)中令x=a,y=e2,z=b, 则xyz=0∈Ω, 从而由归纳假设性质(P2)及式(4), 有

2)对任意a∈A,m∈M, 在式(1)中令x=a,y=m,z=e2, 则xyz=am∈Ω, 从而由归纳假设性质(P2)及引理1和引理2, 有

类似地, 可以证明3)成立.证毕.

引理4对任意的n∈,a1,a2∈A,b1,b2∈B, 有:

证明: 1)对任意的a1,a2∈A,m∈M, 设p,q∈.由归纳假设性质(P2)及引理3, 一方面有

(6)

另一方面有

(7)

比较式(6)和式(7), 得

进而由M的忠实性, 得

(8)

从而可得

(9)

类似地, 可以证明2)成立.证毕.

引理5对任意的n∈,a∈A,m∈M,b∈B, 有:

1)dn(a+m)=dn(a)+dn(m);

2)dn(m+b)=dn(m)+dn(b).

证明: 1)对任意的a∈A,m∈M , 在式(1)中令x=a+m,y=z=e2, 则xyz=m∈Ω.由归纳假设性质(P2)及引理1～引理4, 有

从而有

e1dn(a+m)e2=e1dn(a)e2+dn(m).

(10)

对任意的a∈A,m,m1∈M, 在式(1)中令x=a+m,y=m1,z=e2, 则xyz=am1∈Ω.由归纳假设性质(P2)及引理1～引理4, 有

从而可得(dn(a+m)-dn(a))m1=0, ∀m1∈M.进而由引理1及M的忠实性, 得

e1dn(a+m)e1=e1dn(a)e1.

(11)

于是由式(10),(11)及引理1和引理2, 可得

dn(a+m)=e1dn(a)e1+e1dn(a)e2+dn(m)=dn(a)+dn(m).

类似地, 可证明2)成立.证毕.

引理6对任意的n∈,a1,a2∈A,m1,m2∈M,b1,b2∈B, 有:

1)dn(m1+m2)=dn(m1)+dn(m2);

2)dn(a1+a2)=dn(a1)+dn(a2);

3)dn(b1+b2)=dn(b1)+dn(b2).

证明：1)对任意的n∈,m1,m2∈M, 在式(1)中令x=e1+m1,y=m2+e2,z=e2, 则xyz=m1+m2∈Ω.由归纳假设性质(P2)及引理1～引理5, 有

2)对任意的a1,a2∈A,m∈M, 由归纳假设性质(P2)及引理1～引理6中1), 有

从而可得(dn(a1+a2)-dn(a1)-dn(a2))m=0, ∀m∈M.进而由M的忠实性, 得

e1dn(a1+a2)e1=e1dn(a1)e1+e1dn(a2)e1.

(12)

下证e1dn(a1+a2)e2=e1dn(a1)e2+e1dn(a2)e2.对任意的a1,a2∈A, 由引理1、 引理2、 引理4及归纳假设, 有

从而有

e1dn(a1+a2)e2=e1dn(a1)e2+e1dn(a2)e2.

(13)

进而由式(12),(13)及引理2, 可得

类似地, 可以证明3)成立.证毕.

引理7对任意的n∈,a∈A,m∈M,b∈B, 有dn(a+m+b)=dn(a)+dn(m)+dn(b).

证明: 对任意的n∈,a∈A,m,m1∈M,b∈B, 在式(1)中令x=a+m,y=m1,z=e2, 则xyz=am1∈Ω.由归纳假设性质(P2)及引理1～引理5, 有

从而由M的忠实性, 得

e1dn(a+m+b)e1=e1dn(a)e1.

(14)

类似地, 可证

e2dn(a+m+b)e2=e2dn(b)e2.

(15)

下面只需证明e1dn(a+m+b)e2=e1dn(a)e2+dn(m)+e1dn(b)e2即可.对任意的n∈,a∈A,b∈B, 有

从而有

(16)

类似地, 得

(17)

对任意的n∈,m∈M, 有

从而有

(18)

在式(1)中令x=e1,y=a+m,z=e2, 则xyz=m∈Ω.由归纳假设性质(P2)、 引理1～引理5及式(16)～(18), 有

从而可得

e1dn(a+m+b)e2=e1dn(a)e2+dn(m)+e1dn(b)e2.

(19)

进而由引理2及式(14),(19), 可得

下面证明定理1.由引理5～引理7可证D在三角代数U上是可加的.对任意的x,y∈U,n∈, 设x=a1+m1+b1,y=a2+m2+b2(其中:a1,a2∈A;m1,m2∈M;b1,b2∈B), 由引理1～引理4, 有

即D={dn}n∈是U上可加的高阶导子.证毕.

设H是数域F上的一个Hilbert空间, B(H )表示H上全体有界线性算子, N 表示H中一个包含H和{0}的全序闭子空间链, 若N在集合的交和闭线性张运算下封闭, 则称N为套, N={H,{0}}称为平凡套, 套N相应的套代数记为Alg N, 定义为Alg N={T∈B(H ):TX⊆X, ∀X∈N }.显然, 每个非平凡的套代数都是三角代数, 每个有限维的非平凡套代数都同构于上三角分块矩阵代数.

由于套代数和上三角分块矩阵代数是两类特殊的三角代数, 因此作为定理1的应用有如下推论:

推论2设N是数域F上无限维Hilbert空间H上的一个非平凡套,D={dn}n∈是套代数Alg N上的一个局部非线性三重高阶可导映射, 则D={dn}n∈是一个可加的高阶导子.