插口式钢管模板支架风险分析模型研究

胡长明,王 娟,梅 源,鲍晓强,张延杰

(西安建筑科技大学土木工程学院,陕西 西安 710055)

在工程建设过程中,模板支架体系作为临时承重结构具有十分重要的作用,搭设质量合格、经济合理的模板支架体系对整个工程的顺利完成至关重要[1]。插口式钢管模板支架作为一种新型支架体系,安装和拆除方便快捷,施工效率高,已广泛应用于实际工程。然而,由于横杆的不连续性导致模板支架在使用过程中存在安全隐患,且没有专门的规范指导模板支架的应用,因此,有必要对其进行科学研究。目前,仅本课题组对插口式模板支架的承载力进行了试验研究和数值模拟[2-3],结果表明,立杆间距和横杆插头楔紧度对模板支架承载力影响较大,模板支架在达到竖向承载力时容易发生扭转。

插口式钢管模板支架在搭设和施工过程中存在许多不确定性,如钢管抗压屈服强度的不确定性、材料参数和搭设参数的不确定性等[4-5],从而带来各种风险。风险是指损失发生的不确定性,是失效事件发生的概率P及失效损失C的函数,即R=f(P,C)。模板支架的P和C通常根据资料中历史数据统计得到,然而在实际情况中统计数据往往只考虑到模板支架的随机不确定性,忽视了其本身所具有的模糊不确定性。随机不确定性是在事件发生的不确定性中表现出来的条件上的不确定性,事物本身的形态和类属是确定的;模糊不确定性则是事物本身形态和类属上的不确定性,它是一种比随机不确定性更深刻的不确定性,其存在更为广泛。因此,对P和C进行模糊化处理是有必要的,在风险分析中使决策更接近现实情况。目前,对钢管模板支架方案进行的风险研究较少,仅袁雪霞等[6]建立了扣件式钢管模板支架方案的模糊风险分析模型,但其模型采用的是对称的三角模糊数,不具有一般性,而关于插口式钢管模板支架的相关研究尚未见报道。

本文在模板支架可靠度分析和模糊集理论的基础上,采用非对称三角模糊数及其对应的运算法则和排序方法,对插口式钢管模板支架风险进行分析,兼顾安全性和经济性,旨在为支模方案的选择提供有效而科学的依据。

1 模板支架可靠度分析

图1 模板支架Fig.1 Tubular steel supporting system

课题组前期的试验研究和施工现场实测分析[7]表明,插口式钢管模板支架体系的主要失效模式有:支架立杆失稳破坏、支架水平杆弯曲破坏和支架节点破坏。假设模板支架体系为串联体系,则任何一种失效模式出现均会导致整个体系失效。支架立杆(图1)承受轴力,会发生失稳破坏;支架水平杆(图1)承担木龙骨传来的荷载,会发生弯曲破坏。支架节点破坏包括节点承盘变形破坏、横杆插头滑落破坏等,对该种破坏模式目前缺乏相关统计资料,故本文仅针对支架立杆失稳破坏和支架水平杆弯曲破坏进行可靠性分析。

支架立杆失稳破坏对应的功能函数为

Z1=k1R(A,φ,f)-N(G,Q,l1,l2)

(1)

式中:k1——立杆实际稳定承载力与计算稳定承载力的比值;R——立杆的计算稳定承载力;A——立杆的横截面面积;φ——立杆的稳定系数;f——钢管的屈服强度;N——立杆承担的轴向压力;G——恒荷载;Q——活荷载;l1——支架的纵距;l2——支架的横距。

支架水平杆弯曲破坏对应的功能函数为

Z2=k2Wf-M(G,Q,l1,l2)

(2)

式中:k2——水平杆实际受弯承载力与计算受弯承载力的比值;W——水平杆的截面抵抗矩;M——水平杆承担的最大弯矩。

如果能已知上述功能函数中出现的基本变量的概率分布,则可利用Monte Carlo数值模拟法对插口式钢管模板支架体系可靠度进行分析。

1.1 荷载概率模型

模板支架上作用的荷载包括永久荷载、可变荷载和偶然荷载。永久荷载主要包括新浇筑的钢筋混凝土、模板和支架等的自重[8];可变荷载包括施工活荷载(即施工人员和施工设备的质量、振捣混凝土时产生的振动荷载等)和风荷载[9];偶然荷载包括爆炸、地震等产生的荷载[10-13]。风荷载对处于结构内部且迎风面较小的模板支架的影响很小,而偶然荷载在施工期间出现的概率极低,因此,本文对这2种荷载不予考虑。

目前,确定荷载概率模型的模板支架荷载统计资料相对欠缺。本文根据相关研究结果,在分析中取永久荷载的平均值与标准值之比为1.05,变异系数为0.30,服从正态分布[14];取可变荷载的平均值与标准值之比为0.85,变异系数为10.6,服从极值Ⅰ型分布[14]。

1.2 材料物理性能概率模型

模板支架的材料物理性能参数主要指f。钢管的质量、制作工艺、外形尺寸、使用环境都会引起f的不确定性。钢管材料采用Q235A级钢时,根据文献[15],f服从对数正态分布,平均值取298.5 MPa,变异系数取0.08。

1.3 几何参数概率模型

模板支架的几何参数包括钢管的外径D和壁厚t,以及立杆的步距H、纵距l1和横距l2。插口式模板支架的构件为定型产品,除了D和t,H指节点承盘之间的垂直距离,l1和l2指每个横杆两端节点插头之间的水平距离,其不确定性均主要由制作尺寸的偏差引起。根据课题组对10余个工程施工现场进行的数据调查结果,对随机抽样的数据进行分布假设检验,结果表明上述几何参数均服从正态分布,统计结果如下:D的平均值为47.91 mm,变异系数为0.020 7;t的平均值为2.446 mm,变异系数为0.223 5;H的平均值与标准值之比为1.000,变异系数为0.003 7;l1和l2的平均值与标准值之比为1.002,变异系数为0.005 1。

1.4 承载力概率模型

承载力的不确定性主要由计算中采用的基本假定和公式的不精确引起。

支架立杆的稳定承载力与k1、φ、A及f有关。k1反映的是薄壁轴心受压构件稳定承载力的不确定性,根据文献[16],其服从正态分布,平均值为1.08,变异系数为0.1。φ尽管与H、D、t等有关,但很难建立起显式关系,因此本文采用内插法[6]确定,即根据H确定立杆的计算长度l0,根据D和t确定截面的回转半径i,然后根据λ0=l0/i确定立杆的长细比λ0,最后根据GB 50018—2002《冷弯薄壁型钢结构技术规范》[17]中的φ值表,利用线性插值法确定λ0对应的φ。A可采用D和t表示。因此,支架立杆的稳定承载力可由k1、φ、D、t及f等变量表示出来。

支架水平杆的受弯承载力与k2、W及f有关。k2反映的是薄壁型钢受弯构件承载力的不定确性,目前缺少相关资料,由于受弯构件承载力的不确定性与偏心受压构件相似,k2可采用薄壁型钢偏心受压构件承载力的不确定性统计资料,根据文献[16],其服从正态分布,平均值为1.14,变异系数为0.11。W可采用D和t表示。因此,支架水平杆的受弯承载力可由k2、D、t及f等变量表示出来。

2 基于模糊理论和可靠度分析的模型

2.1 失效概率和失效损失的模糊化

模糊数是定义在实数域R上的一类特殊的模糊集合[18-19],它在模糊数学理论研究、模糊有限元分析和模糊优化的理论和计算技术中起着重要的作用。三角模糊数是其中一类,设A=(a1,a2,a3)、B=(b1,b2,b3)为2个三角模糊数,m为任意实数,定义三角模糊数的广义加法运算和标量乘法运算[20]为

A⨁B=(a1+b1,a2+b2,a3+b3)

(3)

mA=(ma1,ma2,ma3)

(4)

由于2个正三角模糊数相加后仍为1个正三角模糊数,而2个正三角模糊数相乘后的结果则不再是三角模糊数,这就给实际应用带来一些不便,故这里再介绍一下三角模糊数的广义乘法[21-22],即

A⊗B=(a1,a2,a3)⊗(b1,b2,b3)=C=(c1,c2,c3)

(5)

其中

c1=a2b2+(a2-a1)(b2-b1)-a2(b2-b1)-b2(a2-a1)

c2=a2b2

c3=a2b2+(a2-a1)(b2-b1)+a2(b2-b1)+b2(a2-a1)

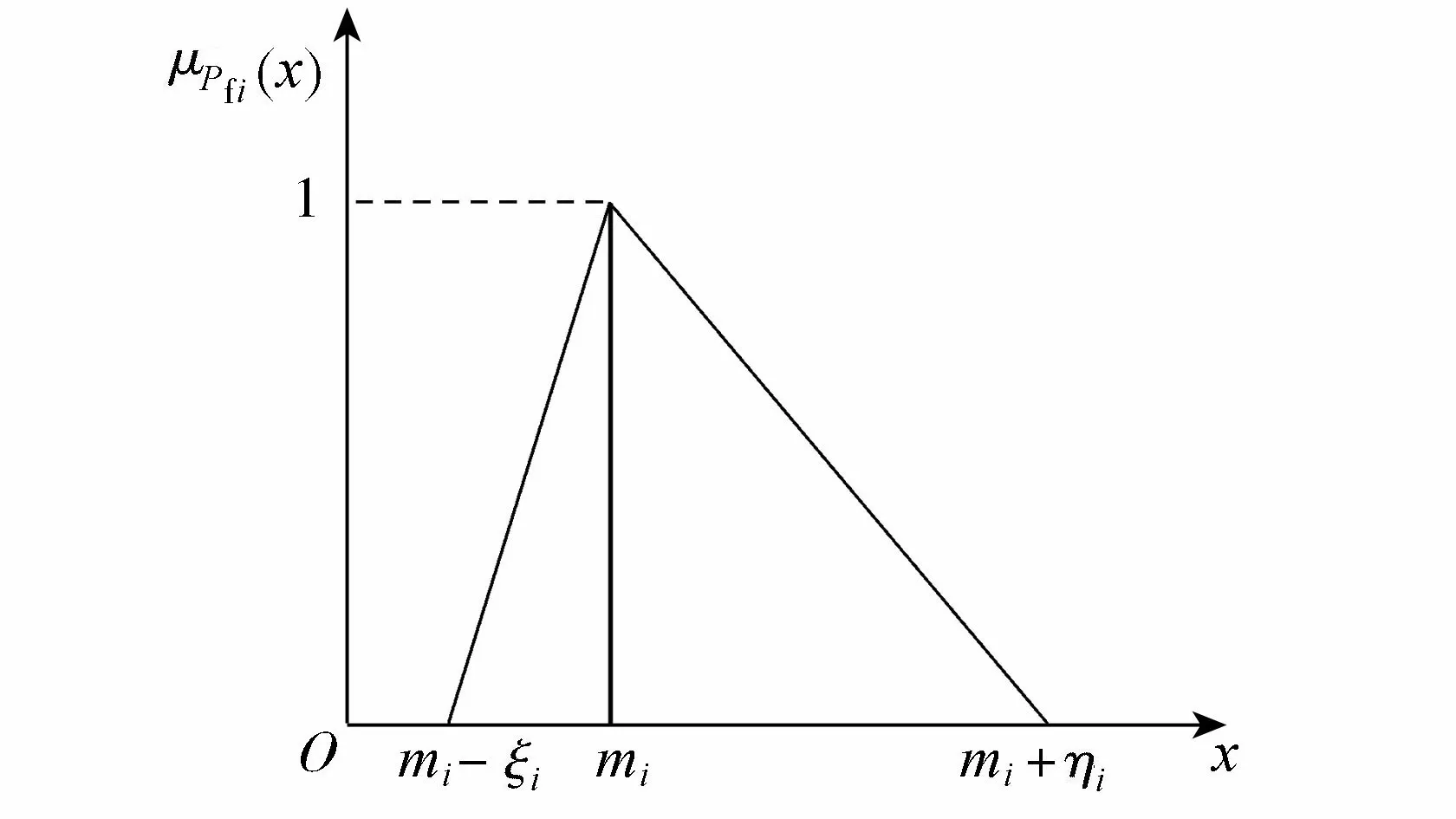
图2 失效概率隶属度函数Fig.2 Membership function of failure probability

根据模板支架倒塌事故的特点,可以假定其失效概率的隶属函数满足三角模糊数,如图2所示,其表达式为

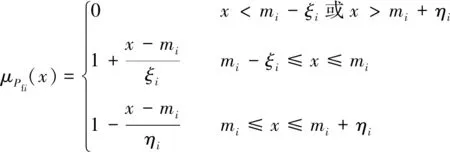
(6)

Pfi=(mi-ξi,mi,mi+ηi)=[(mi-ξi)+

ξiδ,(mi+ηi)-ηiδ] (∀δ∈[0,1])

(7)

式中:Pfi——第i种风险发生的概率,即失效概率。

为了得到ξi和ηi的值,根据人因可靠性的统计数据[23-24],假设当x左偏离其主值50%且右偏离其主值60%时,μPfi≤0.1,可得到

(8)

则ξi=0.556mi

(9)

(10)

则ηi=0.667mi

(11)

根据模糊集理论的论述,运用式(7)～(11)可以对失效概率进行模糊化,从而得到模糊失效概率。

模板支架失效损失费用与其初始投资有关,初始投资越大,失效损失费用越高,失效损失费Cf用与初始投资C0的关系可以表示为

Cf=λC0

(12)

式中:λ——常数。

因为失效损失通常还与其他一些因素有关,如社会因素和自然因素等,所以将其视为一个精确量是不够合理的,将λ按照式(7)～(11)进行模糊化更符合实际情况。

2.2 模糊风险模型的建立

随着不确定性因素的增多,描述模板支架风险的精确性也会随之下降。按照运算法则(式(3)～(5)),可将某一个模板支架方案的风险损失期望值[25]表示为模糊数E(R):

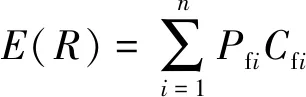
(13)

式中:n——风险种数;Cfi——第i种风险发生的损失大小。

可将风险发生概率Pfi和风险损失Cfi用三角模糊数表示为

Pfi=(Pfi1,Pfi2,Pfi3)

(14)

Cfi=(Cfi1,Cfi2,Cfi3)

(15)

2.3 风险损失期望值排序方法

为了选择最优的设计方案,需要将各个备选方案的损失期望值进行排序,借鉴概率论中均值的概念,定义三角模糊数A的均值m(A)表达式[26]为

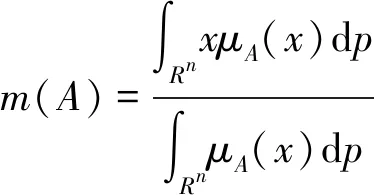
(16)

式中:μA(x)——三角模糊数A的隶属函数。

当模糊数A=(a1,a2,a3)为三角模糊数时,均值m(A)的表达式可简化为

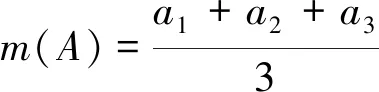
(17)

一般来讲,一个模糊数的均值越大,则排序指标I(A)越大,表明该模糊数越大。

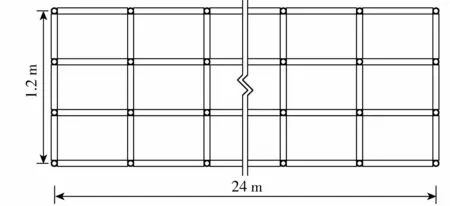
图3 插口式模板支架平面布置示意图Fig.3 Layout of socket-type formwork supporting system

3 算 例 分 析

3.1 方案简介

现浇型钢混凝土转换梁,跨度24 m、高度1 800 mm、宽

度800 mm,梁侧的楼板厚度120 mm。梁下部设插口式钢管模板支架,横向采用4根承重立杆,总高度9.4 m,步距1.2 m。在立杆顶端设可调支托座,搭设构造符合《建设工程高大模板支撑系统施工安全监督管理导则》[27]的规定,模板支架的平面布置如图3所示。永久荷载和可变荷载的标准值分别为50.9 kPa和2.0 kPa。

经过设计计算,以下3种模板支架施工方案均满足要求。方案一:立杆横距400 mm,纵距800 mm;方案二:立杆横距400 mm,纵距600 mm;方案三:立杆横距400 mm,纵距400 mm。试选择最经济合理的方案。

3.2 失效损失

设方案一的初始投资为C0,方案二和方案三则需要投入更多的材料费及人工费,设方案二和方案三的初始投资分别为1.2C0和1.3C0。由式(12)可知Cf=λC0,由式(9)和式(11)知ξλ=0.556mλ,ηλ=0.667mλ,故

λ=(mλ-ξλ,mλ,mλ+ηλ)=(mλ-0.556mλ,mλ,mλ+0.667mλ)=(0.444mλ,mλ,1.667mλ)

(18)

表1 失效概率模糊化相关参数

3.3 失效概率

针对立杆失稳破坏和水平杆弯曲破坏2种失效模式功能函数的变量,采用Monte Carlo法生成随机数,分别计算3种方案对应的可靠指标β,从而失效概率Pf可确定,然后根据式(11)～(13)得到3种方案的模糊失效概率Pfi,如表1所示。

3.4 风险分析

综合考虑各模板支撑方案的各个因素,得到表2所示的结果。

表2 模板支撑方案决策信息

按照式(15)计算各方案的风险损失期望值E(R)。方案一的损失期望为

E1(R)=(0.287 7,1.459 5,3.533)×10-2⊗(0.444mλ,mλ,1.667mλ)C0⨁(0.995 1,0.985 4,0.995 1)C0=

(0.002 877mλ+0.977 3,0.014 595mλ+0.985 4,0.035 33mλ+0.995 1)C0

(19)

E1(R)的均值为

m(E1)=(1.76×10-2mλ+1)C0

(20)

同理,可得到方案二及方案三的损失期望值及其对应的均值:

E2(R)=(0.000 858mλ+1.193 22,0.004 356mλ+1.195 6,0.010 55mλ+1.198 55)C0

(21)

m(E2)=(5.253×10-3mλ+1.2)C0

(22)

E3(R)=(0.000 934mλ+1.297 7,0.001 495mλ+1.298 5,0.002 979mλ+1.299 5)C0

(23)

m(E3)=(1.803×10-3mλ+1.3)C0

(24)

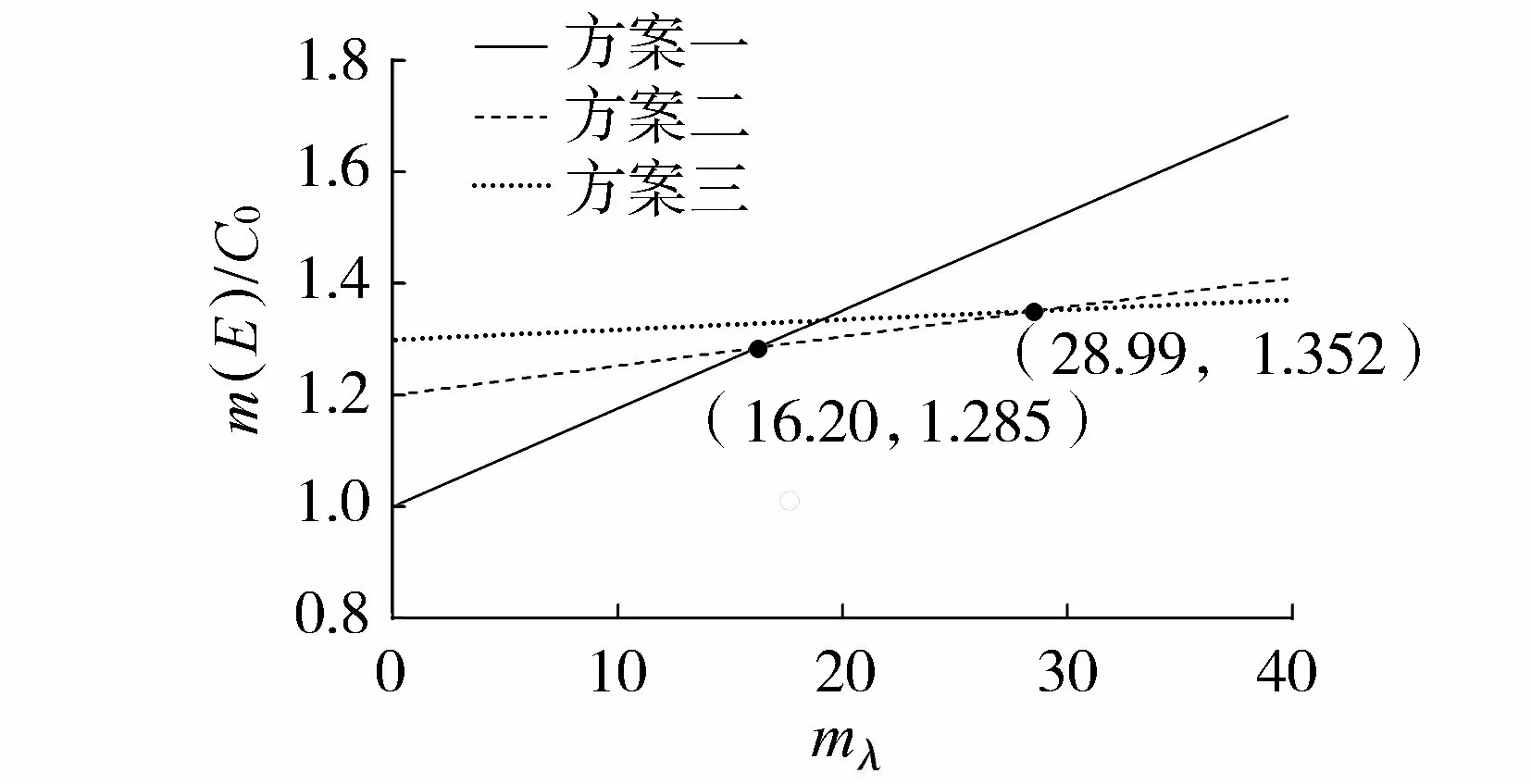
图4 m(E)/C0与mλ的关系Fig.4 Relationship between m(E)/C0 and mλ

为反映mλ的变化对分析结果的影响,图4给出了m(E1)/C0、m(E2)/C0和m(E3)/C0与mλ的关系。

由图4可知,m(E1)随着mλ的增加递增幅度最大,m(E2)次之,增加幅度最小的是m(E3),该变化趋势与实际情况相符。方案一的初始投资最小,但其安全性相对较低,随着失效损失的增加其损失期望值增加较快;方案二和方案三的初始投资依次增大,其安全性依次提高,相对应的损失期望值增长幅度也依次平缓。当mλ<16.20时选择方案一最合理,此时m(E1)最小;当16.20≤mλ≤28.99时,选择方案二最合理,此时m(E2)最小;当mλ>28.99时选择方案三最合理,此时m(E3)最小。

本文采用的概率模型均为调研或试验所得,较为合理,而模糊理论是一种较成熟的数学方法,因此本文结合上述二者提出的插口式钢管模板支架风险分析模型较准确。

4 结 论

a. 本文提出了插口式钢管模板支架体系的主要失效模式,并给出相应的功能函数。通过对基本变量概率分布的确定,对插口式钢管模板支架体系可靠度进行了分析。

b. 结合模糊理论对各参数进行模糊化,使其成为非对称三角模糊数,进而建立了适用于插口式钢管模板支架体系的风险分析模型,并结合实际案例进行计算,最后根据计算结果对3个方案进行了分析。

c. 本文方法简单实用,能够适用于插口式钢管模板支架决策方案选择,从而通过适当调整模板支架方案来获得较好的经济效益,具有较强的实用性。