基于补偿透射率和自适应雾浓度系数的图像复原算法

杨燕，王志伟

（兰州交通大学电子与信息工程学院，甘肃 兰州 730070）

1 引言

在雾、霾等常见不佳天气状况下，由于空气中存在大量介质粒子，会对户外图像采集系统造成很严重的干扰，使得到的图像或实时视频质量下降，严重影响此类信号的实际应用价值。因此，对户外系统采集得到的图像进行清晰化处理和复原有重要的研究意义。

从目前的研究现状而言，为了能使计算机视觉系统做出更精确的判断或识别，雾天图像恢复起着重要的预处理作用，因此去雾处理是计算机视觉和图像领域共同关注的热点。早期的去雾算法主要基于图像增强，代表性算法有直方图处理[1]和Retinex理论[2]等。但是这类方法只是简单地改善了亮度和色彩，并没有仔细考虑成雾原因，得到的处理效果也较为一般。

近年来，基于图像复原的方法得到了充足的发展，通过反演成雾过程，利用景深信息或先验规律，并结合大气散射模型得到最佳的复原效果。Tan[3]观察到无雾图像的对比度高于有雾图像，从而提出最大化对比度算法，利用马尔可夫随机场（MRF,Markov random field）建模进行优化，该方法能够较好地去除雾气，但是容易失真。He 等[4]基于大量的统计信息，提出了著名的暗通道先验，取得了显著的去雾效果，但是不善于处理包含高亮区域的图像。Zhu 等[5]提出了颜色衰减先验规律，利用机器学习训练得到图像的景深信息和其饱和度与亮度之间的关系，但存在去雾不彻底的问题。Meng 等[6]通过边界约束来限制透射率的范围，使用正则化方法进行优化，但是复原结果有偏色现象。

最近，研究人员提出了很多基于深度学习的复原算法。Cai 等[7]设计了一种基于端对端的网络架构，与现有复原方法中使用的假设先验条件建立联系，获得最终的去雾结果。Ren 等[8]提出了多尺度卷积神经网络用来训练透射率，并以精细尺度的网络进行优化。Liu 等[9]设计了一种新的残差结构，聚合先验知识和雾图信息，用来估计透射率。虽然使用深度学习具有很强的前沿性，但存在的问题是没有大量且真实的数据库，在训练中使用的都是经过合成和渲染的有雾图像数据集，这也导致了使用此类方法并不总能得到最佳和稳定的结果。

基于暗通道先验类的复原算法容易对天空或明亮区域造成失真，且伴随着光晕效应。针对这2个不足，本文设定补偿透射率并利用高斯函数进行拟合，得到优化后的精准透射率。通过分析图像中的雾气特性，提出亮度熵概念，对雾图求取亮通道操作并逐像素处理得到亮度熵信息，辅助于金字塔模型得到纹理特征，获取最终的雾气分布图。建立一种自适应关系求取雾气浓度系数，同时改进局部大气光的求取方法，结合大气散射模型得到复原结果。实验结果表明，本文方法可以取得显著的去雾效果。

2 背景

2.1 大气散射模型

在计算机视觉理论中，通常以大气散射模型[10-11]来描述成雾原理，它是雾天图像具有低对比度、颜色衰退等性质的理论基础，其计算式为

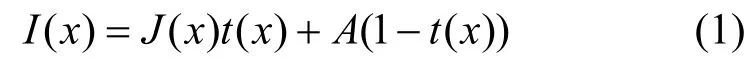
其中，I(x)为有雾图像；J(x)为无雾图像；A为全局大气光；t(x)为透射率，其反映着阳光穿透大气直达成像设备的能力，值越大穿透能力越强；J(x)t(x)为直接衰减项，表示入射光线经过空气中介质粒子散射后的衰减程度；A(1 -t(x))为附加项，表示在成像过程中加入的环境散射光，来源有直射光、大气散射光或地面反射光。当空气中介质粒子分布均匀时，t(x)可表示为

其中，d(x)为景深信息，即成像物体到成像设备之间的距离；β为大气散射系数，表示单位体积的大气对光的散射能力。在去雾问题中，唯一的已知量为I(x)，即通过式(1)来求取结果J(x)是一个病态问题，必须加入其他条件。因此，求取透射率t(x)和大气光值A为算法的关键。

2.2 暗通道先验的不足

He 等[4]提出的暗通道先验在去雾领域取得了突破性的成就，基于对大量户外无雾图像的统计提出一幅无雾图像，除却天空或部分高亮区域，像素值至少在一个{r,g,}b颜色通道中趋于0。暗通道的计算式为

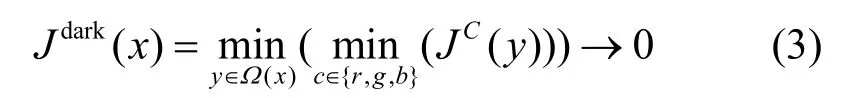
其中，c表示颜色通道，Ω(x)指以像素x为中心的邻域，Jdark(x)被称为暗通道图。结合式(1)对式(3)两边取最小值滤波，可以得到初始透射率t0(x)为

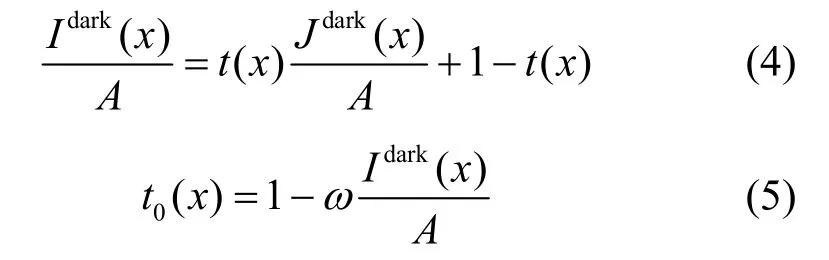
其中，ω是为了保留少量雾气，以免雾气去除太过彻底造成复原效果不自然，通常取ω=0.95。利用式(5)得到的透射率比较粗糙，并不能直接用来复原。因此，He 采用软抠图算法对透射率进行优化，虽然结果有所改善，但是时间复杂度略高。随后又提出较快的引导滤波优化算法[12]，得到了较为满意的效果。

暗通道先验基于统计规律，以一种简便直观的方式来求取关键参数透射率t(x)，但是存在以下2个问题。

1)天空区域透射率估计过小。暗通道清楚地指出其不适用于天空等高亮区域。因为在这些区域，暗通道值并不趋向于0，而是趋于一个较大的值，继而导致实际透射率偏大。但由于采用式(5)计算全局透射率，导致天空区域的透射率估计过小。

2)容易出现光晕效应。获得暗通道的主要步骤为两次最小值滤波，但是在边缘附近采用最小值滤波会造成信息缺失，导致较亮部分被低估，使边缘处的透射率偏大，进而产生光晕效应。

以图1 为例，观察He 算法的处理结果可以发现，在帽子边缘以及山顶与天空的交界处都有稍明显的光圈，就是典型的光晕效应；而且在天空区域有失真现象，偏色严重。而本文算法较好地改善了上述不足，得到了较为满意的效果。

图1 光晕效应及天空失真

3 补偿透射率及自适应雾浓度系数

3.1 补偿透射率

由第2 节内容可知，利用暗通道先验会造成天空等高亮区域的透射率偏小。依据数学推导，提出补偿透射率对其进行修正。在式(4)的基础上，不结合暗通道规律，则有

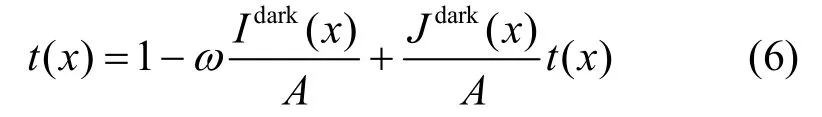
结合式(5)得到

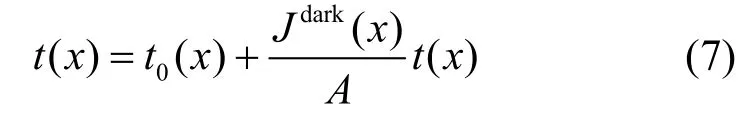
可以发现，利用暗通道求取的透射率t0(x)只是式(7)的一个特例。设，可得到全局透射率t(x)为

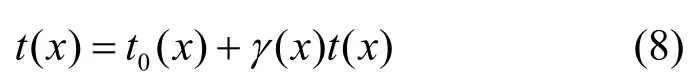
其中，t0(x)为相对透射率，γ(x)t(x)为补偿透射率。通过如此修正，得到的全局透射率t(x)为精准透射率，有效避免了使用相对透射率t0(x)带来的不足。

在RGB 色彩空间中，A、I(x)、J(x)这3 个量共平面且模长依次递减[13]，假设I(x)和J(x)之间存在某种衰减关系，且因为高斯函数具有良好的分布特性以及衰减性质，本文以其来拟合Idark(x)和Jdark(x)之间的关系为

其中，σ为标准差，取值0.15。得到γ(x)后，利用式(10)可得到全局精准透射率t(x)为

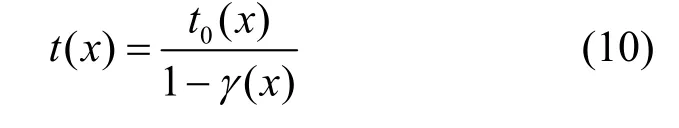
实验对比如图2 所示。图2(a)为一幅含有天空区域的雾图。利用暗通道先验得到的透射率在天空处偏低，如图2(b)所示。而在经过本文算法补偿后天空透射率显著提高，如图2(d)所示。针对复原结果，与He 算法相比，本文算法在天空区域的处理更加彻底，如图2(f)所示。

图2 透射率示意

3.2 雾气分布图

在有雾图像中，雾气的分布及浓度可以被直观察觉，其主要特征是亮度值较高。本文将雾气分布变通理解为亮度信息的混乱程度，在大部分情况下，混乱程度越高，雾气分布越浓越弥散。在物理学中，能够描述混乱程度的概念为信息熵。借此，本文提出以图像的亮度熵信息来反映雾气特征，熵值越大，雾气出现的随机性越高（混乱程度高）。具体步骤为，首先进行两次最大值操作，求取原图的亮通道图Ibright(x)来反映整幅图像的亮度分布信息为

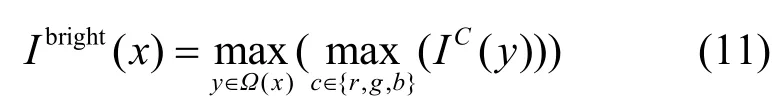
然后利用熵公式即式(12)得到亮度熵信息e为

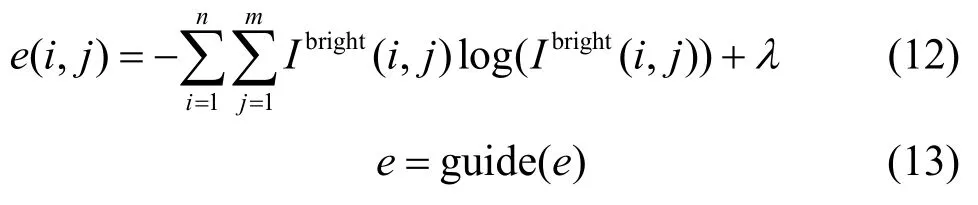
由于采取对数操作，考虑极端情况，会使值为1 的像素点经过变换后变为0，因此λ的作用是避免像素为空值，取λ=0.01，m和n表示图像的长和宽，e(i,j)为某一像素的具体熵值。由于得到的初始亮度熵信息比较粗糙，故采用引导滤波进行降噪平滑处理，guide 表示引导滤波操作。

单纯的亮度熵信息无法充分体现出雾气分布情况，需配合原始图像的纹理特征d。本文采用在尺度空间中满足视觉不变性的高斯金字塔[14]来拟合人眼在不同观察尺度下的模糊程度。

算法1纹理特征获取

输入有雾图像I(x)

输出将上采样的结果作为纹理特征e

Step1转换成灰度图进行高斯模糊，窗口大小为15×15 。

Step2对模糊后的图像进行下采样，尺寸缩小为原图尺寸的

Step3对下采样后的图像继续进行高斯模糊。

Step4对模糊后的图像继续下采样，尺寸缩小为原图尺寸的

Step5对大小的模糊图像进行上采样，达到原图尺寸。

结合纹理特征和亮度熵信息，利用式(14)可得到最终的雾气分布图DisH 为

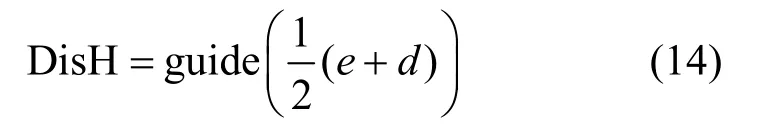
为了充分验证本文提取雾气分布方法的有效性，分别选取高亮度清晰图像和有雾图像，进行雾气提取操作，结果分别如图3 和图4 所示。可以发现，高亮度清晰图像的直方图分布比较集中，趋向于端分布，且DisH 分布主要集中在高亮背景部分，而其余部位无法体现出分布特性，如图3(b)和图3(e)所示，其中横坐标为像素值，纵坐标为对应像素的个数。在有雾图像中，因雾气充满整幅图像，直方图分布跨度稍大，如图4(b)和图4(e)所示。不再集中于部分区域，导致DisH 中的亮度分布较为广泛，直观上很好地拟合了雾气分布，也证明了所提方法的可行性。

3.3 自适应雾浓度系数

He 等为了避免彻底去除雾气而导致复原结果不自然，将式(5)中ω取为定值0.95。但是针对不同图像，例如浓雾情况会造成去雾不彻底，薄雾产生失真；且ω的值不宜太小，否则不能体现去雾效果，一般情况下，ω的取值范围为[0.8,1]。本文在得到雾气分布DisH 的基础上，建立一种线性关系来自适应求取ω。在求取亮度熵信息e的过程中，因为采用了对数变换而导致像素被压缩，使雾气分布图DisH 的像素整体偏低。令m表示DisH 的最小值，M为最大值，mean 为均值，建立

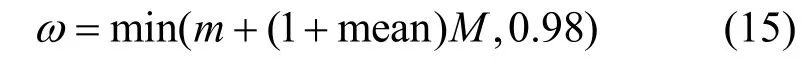
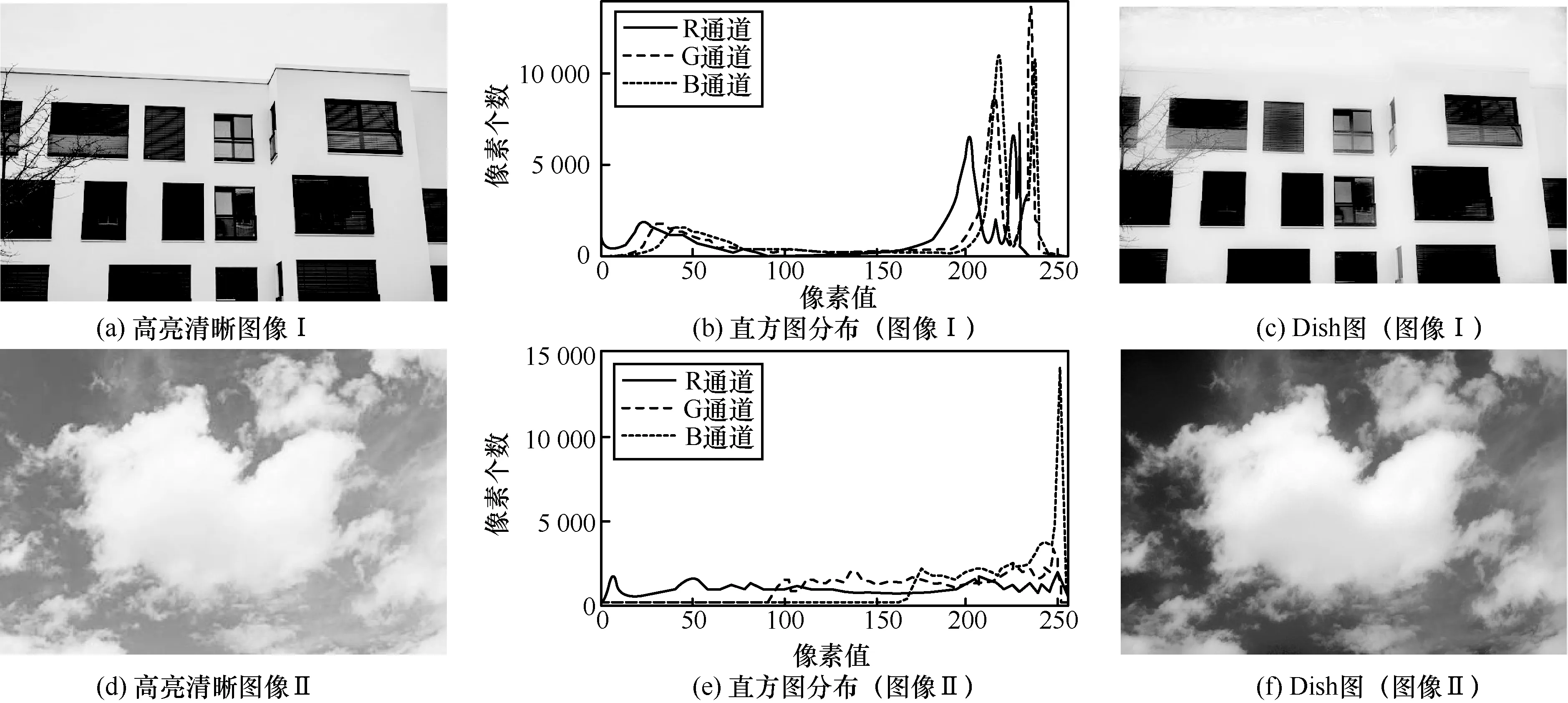
图3 无雾高亮图像DisH 及对应的直方图分布

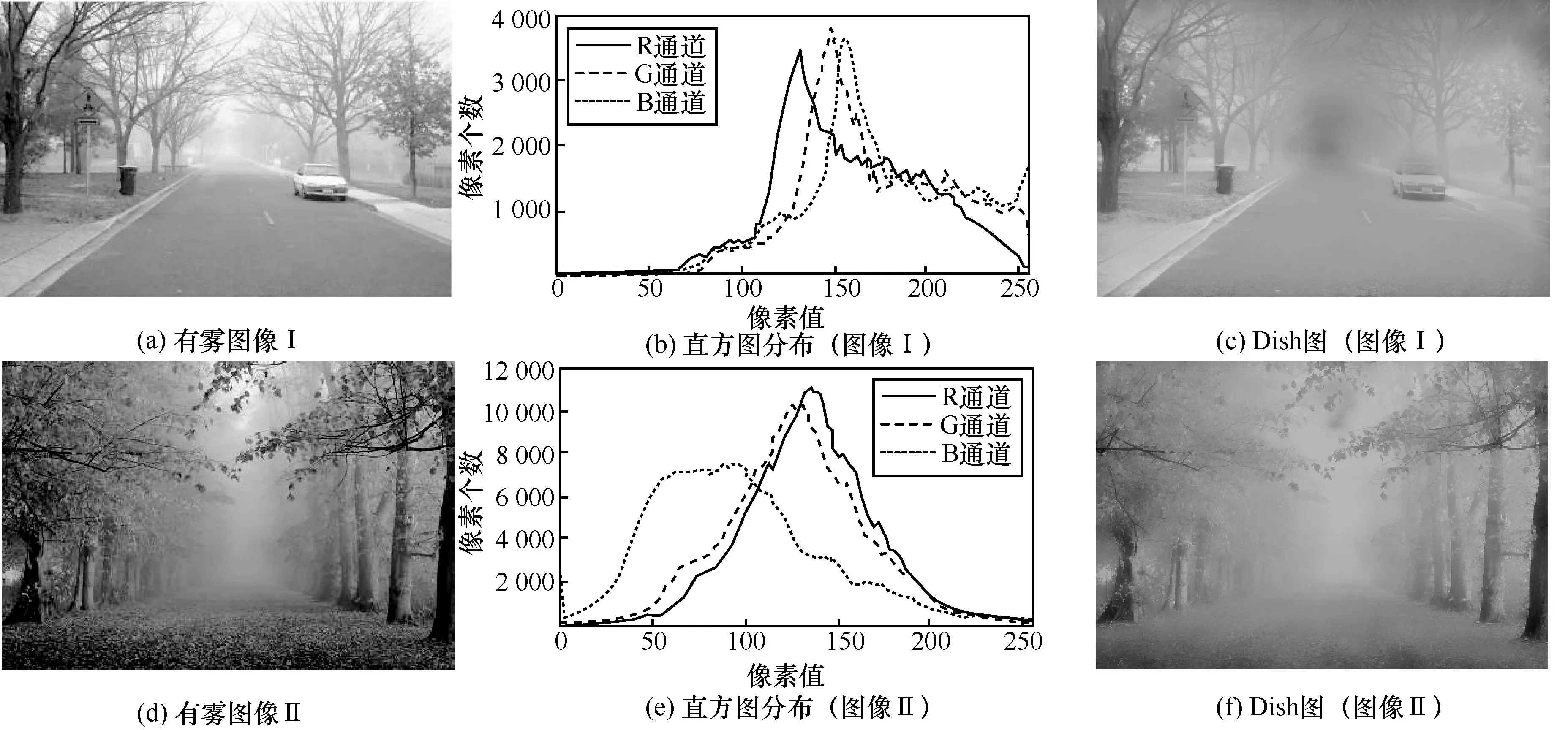
图4 有雾图像DisH 及对应的直方图分布

以m为初始截距，1 +mean为斜率对M进行提高，同时为防止ω溢出，取最大值0.98 进行抑制，线性变换如图5 所示，其中i、j表示归一化后的像素值，单位为1。

由于浓雾情况下M和mean的值一定大于薄雾，即浓雾情况下ω较大，进而得到较小的透射率，使去雾程度更加彻底。相对应地，薄雾情况下可得到偏小的ω，较大的透射率可以保护图像不会过度失真，维持较好的复原效果。分别选取不同雾浓度的图像进行对比，结果如图6 所示。在图6(a)中，经过本文自适应处理后的ω取值为0.92，小于定值0.95，从复原结果看，采用定值的He 算法透射率偏小，造成了部分近景失真，如图6(b)方框所示，而本文稍大的透射率较好地维持了原图特性。而在图6(d)里，本文自适应处理后的ω取值为0.97，大于定值0.95，拥有稍小的透射率，去雾程度也更加彻底，如图6(f)所示，而He算法则留有稍许残雾，如图6(e)方框所示。

3.4 大气光值

去雾问题中另一个关键参数就是大气光值A。若选取的大气光值大于真实值，复原图像将会偏暗并丢失部分细节，反之复原结果偏亮。He 等选取暗通道图中前0.1%最亮像素对应于原图的像素作为大气光值，该方法在大部分情况下较为准确，但当包含高亮度区域时会错误定位，高估A值。Sun 等[15]提出了局部大气光估计，从局部考虑，减弱全局估计造成的误差。具体步骤为：首先求取有雾图像三通道的最大值，然后通过形态学闭操作消除内部高亮细节，再采用交叉双边滤波平滑处理，得到最终结果。因为大气光值反映的是亮度信息，为此只针对亮度信息，本文对Sun 算法做如下改进。

图6 薄雾及浓雾效果对比

算法2改进的大气光求取

输入有雾图像I(x)

输出大气光值A

Step1将I(x)转换到HSV 颜色空间，提取亮度分量V(x)。

Step2对V(x)进行形态学闭操作处理，消除高亮细节。

Step3采用交叉双边滤波平滑处理，得到最终结果。

改进后的大气光和Sun 算法对比如图7 所示。可以发现，本文大气光在部分细节上更加精确，如图7(c)所示。针对复原结果，Sun 算法处理后在边缘处（树叶与墙）存在轻微的光晕效应，如图7(d)所示。而本文结果自然清晰，过渡平缓，取得了较好的复原效果。

在得到大气光值和精确透射率之后，结合大气散射模型，利用式(16)进行最后的复原。为了避免t(x)→ 0时而导致最终的复原结果像素溢出，对t(x)进行最小值限制，设定下限值t0=0.01。

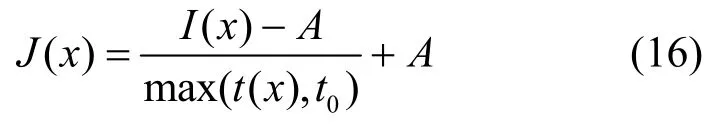
3.5 算法原理

本文通过设定补偿透射率对暗通道透射率进行优化处理，分析雾气特征，引入亮度熵信息并结合高斯金字塔提取的纹理特征得到雾气分布DisH，同时建立自适应线性变换以获取不同雾浓度下的系数ω，求得精准透射率t(x)，结合改进的大气光值求取方法，进行图像复原。图8 是本文所提算法每个步骤对应的结果。值得注意的是，由于图8(e)补偿透射率像素较低，不方便观察细节，已采取灰度扩展。可以看出，其最终复原结果颜色逼真，效果自然。

本文算法的执行流程如下。

算法3本文算法

输入有雾图像I(x)

输出复原图像J(x)

Step1利用暗通道先验求取初始透射率t0(x)。

Step2利用高斯衰减拟合补偿透射率γ(x)t(x)，依据式(10)得到精准透射率t(x)。

Step3求取原图的亮通道图Ibright(x),依据式(12)得到亮度熵信息e。

Step4高斯金字塔提取纹理特征d，配合亮度熵信息得到雾气分布DisH。

Step5根据所建立的自适应线性关系得到雾气浓度系数ω。

图7 大气光对比及实验

图8 复原示例

Step6提取原图亮度信息，改进局部大气光算法得到大气光值。

4 实验分析

为了验证所提算法的有效性和可行性，本文进行了大量的对比实验。一方面使用经典算法对比真实场景下的有雾图像，从主客观方面依次评价；另一方面采用目前在深度学习领域里比较常用的数据集评判，本文选取合成去雾数据集[16]。实验环境为Matlab(R2016a)，运行系统为Windows7。

4.1 主客观评价

选取6 幅不同性质的图像分为近景组、远近景交替组和远景组图像，分别与He 算法[4]、Meng 算法[6]、Ren 算法[8]和Liu 算法[9]进行复原结果的对比，前2 种方法是基于复原类的经典方法，后2 种则是基于深度学习类的方法。为了建立更加全面的分析体系，从主客观方面依次进行评价。

图9 是一组具有丰富近景的图像。从图9 可以看出，本文在拥有较好去雾效果的同时能保持原图近景特性，没有过度失真现象，亮度适宜；He 算法和Meng 算法处理后的效果存在轻许偏色现象，分别如图9(b)和图9(c)所示；Ren 算法和Liu 算法利用深度学习来进行复原，处理结果较为优良，但是由于没有大量且真实的雾天训练数据，而是采用合成渲染的数据集，导致其效果不稳定。

图10 是一组远近景交替组图像。从图10 可以看出，本文在景深渐远处去雾程度彻底，这是因为采用了补偿透射率，而且颜色更加自然；He 算法处理后的效果偏暗，是由于ω取为定值导致透射率过小，造成近景失真；Meng 算法对天空恢复较好，但由于采用最亮像素为大气光值，造成结果偏暗如图10(c)所示；Ren 算法和Liu 算法处理后对近景特性保持得很好，但是存在颜色偏移问题。

图9 近景组图像

图10 远近景交替组图像

图11 远景组图像

图11 是一组含有天空区域图像。从图11 可以看出，本文处理后的效果极好地维持了天空特性；He 算法整体处理效果较优，但是在天空边缘处存在轻微的光晕效应；Meng 算法由于对透射率限制过多，仍存在偏色现象；Ren 算法和Liu 算法在处理此类图像时会产生过饱和现象，导致图像变暗。综上所述，在主观视觉方面，本文处理效果较为自然且细节更加突出，但只凭这样的主观判断并不全面。从客观恢复指标出发进行侧面验证，本文采用常见的客观评价方法[17-19]，评价指标为可见边p、平均梯度r、复原图像饱和点像素个数θ以及运行时间t（单位为s）。其中p和r的值越大表示复原效果越好，θ越小越好。数学计算式为

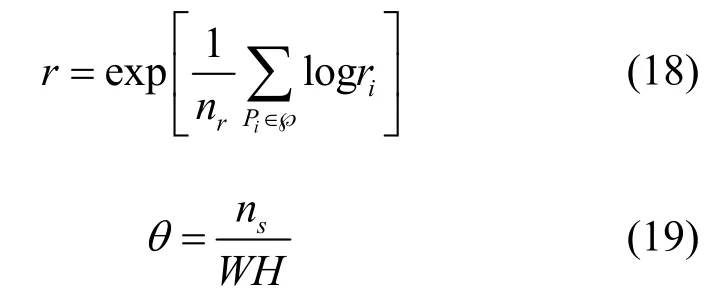
其中，nr和n0表示原图和复原结果的可见边数，ri表示在某一像素处去雾图和原图的平均梯度比，℘表示复原结果可见边集合，ns表示饱和点像素个数，W和H表示图像的宽和高。客观评判里的各项数据分别如表1 和表2 所示。

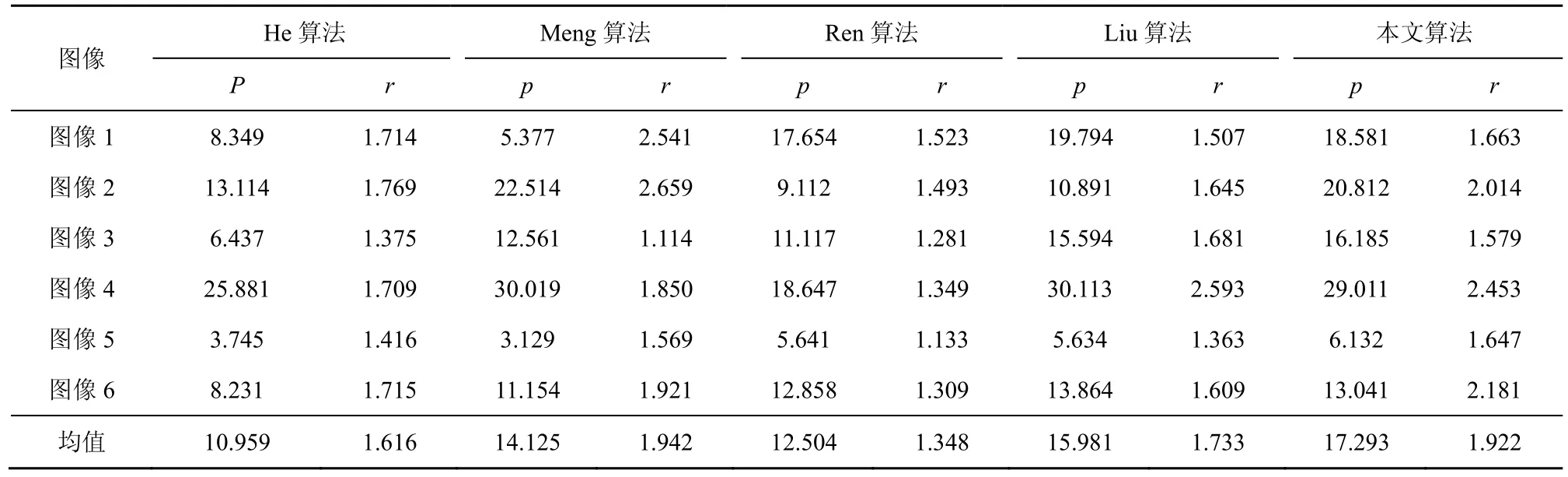
表1 各种算法的e和r指标对比

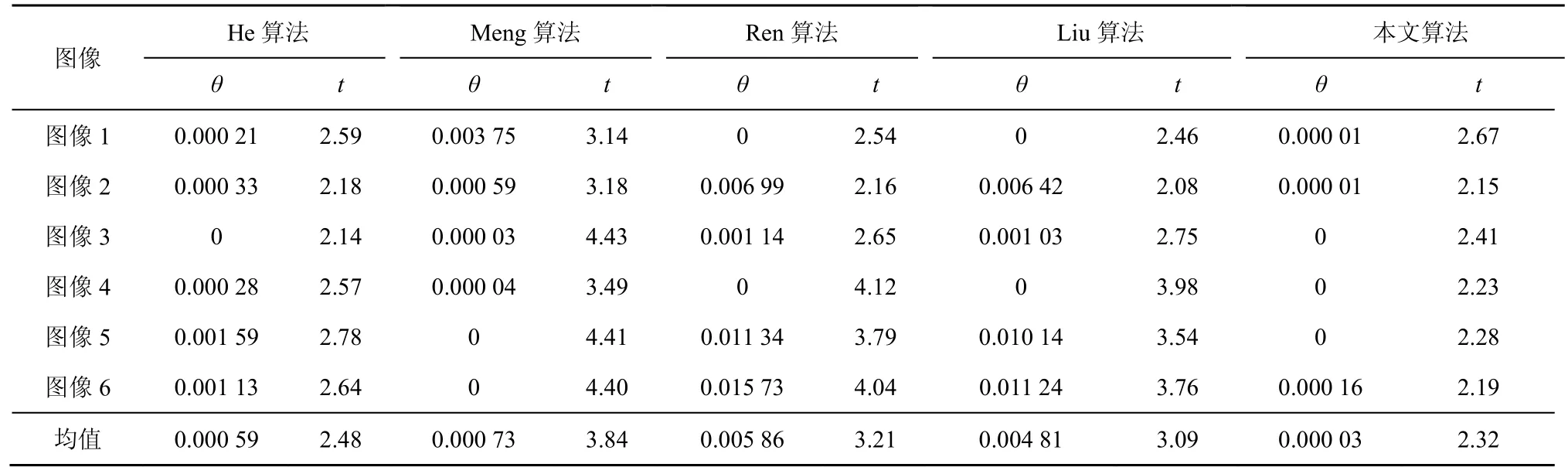
表2 各种算法的θ和t指标对比

由于本文算法复原的无雾图像色彩逼真，近景维持较好，没有饱和现象且去雾较为彻底，在表1 中的可见边指标p上取得了领先的优势，且平均梯度指标r也不弱于其他经典算法。因为本文去雾结果亮度适宜，所以可见边指标θ的均值更低。衡量一种算法是否高效的指标是运行时间，可以看到本文的处理速度较快。综上分析，本文算法更具优势。

4.2 测试集验证

除了对真实场景下的雾图进行对比，本文也使用深度学习领域较为流行的评测方法，即对合成有雾数据集进行比较，随机挑选其中几幅图像用作主观观察，如图12 所示。客观评价指标采用结构相似度（SSIM,structural similarity index measurement）和峰值信噪比（PSNR,peak signal-to-noise ratio）。其中SSIM 是衡量两幅图像相似度的指标，PSNR 是有用信号和噪声比，两者的指标值越大越好。

主观实验结果如图13 所示。从图13 可以看出，本文算法对合成和渲染（非真实）的有雾图像处理效果较好，基本可以做到去除雾气，还能较好地保持近景特性。但存在的问题是处理结果偏暗且有稍许偏色。将所提方法在整个测试集上运行，得到的评分如表3 所示（数值为均值）。

从表3 可以发现，经过本文算法处理后的数据集在性能指标上的评分并不落后于其他算法，而且还有部分领先；同时也具有较快的处理时间，这证明了本文算法的可行性和有效性。

图12 数据集中的有雾图像

图13 数据集本文算法去雾结果

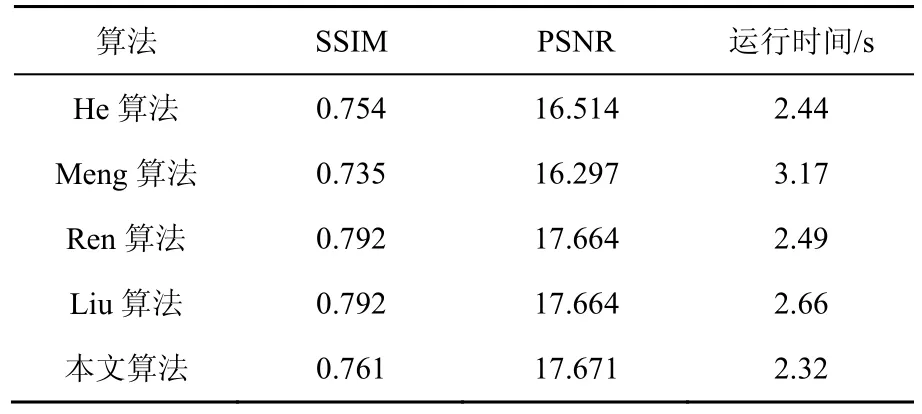
表3 数据集评测数据指标

5 结束语

针对现有雾天图像清晰化处理存在的不足，本文提出了一种基于补偿透射率和自适应雾浓度系数的复原算法。因为暗通道先验不善于处理高亮区域，设定补偿透射率并用高斯函数拟合得到精准透射率；通过分析雾气分布特性，提出图像的亮度熵概念，并辅助与高斯金字塔提取的纹理特征得到有雾图像的雾气分布，建立线性关系自适应求取雾浓度系数；同时改进局部大气光的求取方法，结合大气散射模型得到最终的复原结果。实验结果表明，本文可以恢复得到质量较好的结果。但是该算法也存在着不足，如对有些图像的处理结果偏暗，这也是接下来要改进的地方。