一种基于Levy飞行的改进蝗虫优化算法
赵 然,郭志川,朱小勇
(1.中国科学院声学研究所国家网络新媒体工程技术研究中心,北京 100190; 2.中国科学院大学,北京100049)
0 引 言
蝗虫优化算法(Grasshopper Optimization Algorithm, GOA)是一种元启发式优化算法,可以用来解决任务调度问题[1]。任务调度问题是一种在边缘计算领域常见的问题[2]。边缘终端节点存在较强的异构性,节点资源情况和任务处理速度不同,所以不同的任务调度方案会产生不同的执行结果。一个优秀的任务调度方案可能会对边缘计算系统的服务效果产生很大影响。
任务调度问题是将多个任务调度到多个节点的优化问题[3]。任务调度问题也是一个NP-hard问题[4]。许多元启发式算法(Meta-Heuristic Algorithm)被用来处理边缘计算中的任务调度问题[5]。元启发式算法具有操作简单和开销较少的优点,能够在最优化问题中通过评价、迭代、演进等方式逐步找到全局最优解或近似全局最优解[6]。
粒子群算法(Particle Swarm Optimization, PSO)是一种非常经典的元启发式算法[7-11]。该算法最初是受到鸟群活动规律的启发,通过追随当前搜索到的最优值来寻找全局最优解。近年来,研究人员通过模仿昆虫、鱼类和其他群体生物的自然行为提出了一些新的元启发式算法,包括蚁狮算法[12](Ant Lion Optimizer, ALO)、鲸鱼优化算法[13-14](Whale Optimization Algorithm, WOA)、蜻蜓优化算法[15-17](Dragonfly Algorithm, DA)、蚁群算法[18-20](Ant Colony Optimization)等。2017年,Saremi等人[1]提出了蝗虫优化算法。蝗虫优化算法通过在蝗虫集群内部分享经验,进行多轮迭代演进,不断修正搜索方向,最终找到最优位置或者近似最优位置。
自蝗虫优化算法提出以来,研究人员在此基础上提出了一些改进优化算法,但提升效果不够显著。Ewees等人[21]于2018年提出了基于反向学习的改进蝗虫优化算法(Improved Grasshopper Optimization Algorithm Using Opposition-Based Learning, OBLGOA)。OBLGOA引入了反向学习策略,以生成的反向解作为备选的可行解,使用这种策略可以提高算法的收敛速度,但是由于反向学习策略缺乏随机性,对算法性能的提升效果较为有限。Arora等人[22]于2018年提出了混沌蝗虫优化算法(Chaotic Grasshopper Optimization Algorithm, CGOA)。CGOA引入混沌映射因子来提高算法性能,文献[22]中使用了10种不同的混沌映射因子来测试混沌理论的效果,但是因为不同的混沌因子在处理不同的测试函数的时候效果不同,对算法整体的效果提升也不够理想。
研究人员对于蝗虫优化算法的改进缺乏随机性,也没有考虑算法会陷入局部最优的问题,改进效果不够显著。本文通过引入基于Levy飞行的局部搜索机制和基于线性递减参数的随机跳出策略,提出一种基于Levy飞行的改进蝗虫优化算法,优化算法的搜索性能,并将所提出的改进算法应用于解决边缘计算中的任务调度问题。
1 蝗虫优化算法
蝗虫优化算法模拟了自然界中蝗虫群的迁徙和觅食行为。蝗虫群为了寻找一个有食物的新栖息地,不断进行迁徙。在这个过程中,蝗虫群内部蝗虫之间的相互作用力会对每一个蝗虫个体的位置造成影响。来自蝗虫群外的风的力量和重力也会影响蝗虫集群整体的移动轨迹。另外,对于迁徙过程来说,目标食物的位置也是一个重要的影响因素。
蝗虫优化算法将蝗虫集群抽象为一群搜索单元进行数学建模,借鉴其迁徙和觅食的移动过程的特点。文献[1]提出了蝗虫群体迁徙的数学模型,具体的模拟公式如式(1)所示:
Xi=Si+Gi+AI
(1)
其中,变量Xi为第i个搜索单元的位置,变量Si代表蝗虫集群内部搜索单元之间的相互作用力对第i个搜索单元的影响程度,变量Gi代表蝗虫集群外部重力因素对第i个搜索单元的影响程度,变量Ai代表风力的影响因素。在应用于解决数学优化问题的时候,为了优化数学模型,公式(1)中代表集群外部影响因子的变量Gi和Ai需要被替换为目标食物的位置Td,这样迭代公式变成式(2)所示:
Xi=Si+Td
(2)
其中,变量Si的定义如式(3)所示:
(3)
其中,ub和lb分别表示搜索空间的上界和下界,变量c为搜索单元的搜索舒适区控制参数。其中函数s(r)为计算蝗虫集群之间的社会关系影响因子,该函数定义如式(4):
(4)
其中,e是自然底数,变量f表示吸引力因子,参数l表示吸引力长度。在整个搜索过程中,每个位置的评价指标为适应度函数。在优化问题中,适应度函数通常为所要求解的目标函数,通过适应度函数计算所得到的值为适应度值(fitness)。在任务调度问题中,适应度函数通常是根据具体任务调度模型所建立的评价函数。在优化问题的求解过程中,公式(2)作为演进公式,被不断循环迭代来寻找最优解,每轮迭代得到的最优的适应度值即被视为目前得到的最优解的值,得到的最优解的位置则被视为当前的食物目标位置Td,直到达到迭代次数为止。
2 基于Levy飞行改进蝗虫优化算法
蝗虫优化算法具有简单的理论基础,易于实施。但是原始的蝗虫优化算法缺乏随机因素,几乎没有变化,算法在搜索过程中很容易陷入局部最优。为了解决这些不足,本文提出2个改进方法:基于Levy飞行的局部搜索机制和基于线性递减参数的随机跳出策略。
2.1 基于Levy飞行的局部搜索机制
原始蝗虫优化算法中的所有参数都是确定性的,非常缺乏随机性。这会导致算法在迭代演进的过程中缺乏创造性,每个搜索单元只能搜索相对确定的位置。将随机因子引入到确定性系统中是提高性能的常用方法。
Levy飞行是一种非常有效的提供随机因子的数学方法。Levy飞行可以提供步长符合Levy分布的随机游走方法,Levy分布如式(5):
Levy~u=t-λ, 1<λ≤3
(5)
为了扩展搜索单元的搜索半径,增强算法的随机性以及局部最优值的搜索能力,本节提出一种基于Levy飞行的局部搜索机制。当一次位置更新的迭代过程结束的时候,该机制可以以一定概率通过Levy飞行对每个搜索单元的位置进行局部调整,调整公式的定义如式(6)所示。在某种程度上,Levy飞行可以在搜索单元向着最优解位置搜索的过程中为其提供一定的“视觉”,使得搜索单元可以“看到”它们周围的一片较小的区域内的情况。
X=X+10×c×sts×Levy(dim)×X
(6)
其中,sts是控制飞行方向和变化概率的阈值函数,sts的计算方法如式(7)所示。其中,sign(x)是sign符号函数,xtrans是取值在[-3,3]之间的随机数。
sts=sign(xtrans-1)+sign(xtrans+1)
(7)
2.2 基于线性递减参数的随机跳出策略
蝗虫优化算法的基础理论比较简单,该算法只关注了收敛到全局最优的过程,而忽略了跳出局部最优的机制。因此,蝗虫优化算法的搜索过程很容易陷入局部最优,使得搜索无法更进一步地进行下去。
为了提高蝗虫优化算法的跳出局部最优的能力,本节提出基于线性递减参数的随机跳出策略。当搜索单元搜索到当前最优解的位置的时候,该目标位置可以替换旧的目标位置。如果没有搜索到最优解,则可以开始启动基于线性递减参数的随机跳出策略。该策略的计算方式如式(8):
Xi=(2×(0.5-rand(0,1))+1)×Xi
(8)
其中,Xi是第i个搜索单元的位置。如果新搜索到的Xi拥有更优的适应度值,那么它将会取代原来的Xi,可以认为发生了一次成功的跳出行为。
原始蝗虫优化算法的演进公式仅仅将当前迭代获得的最佳位置作为搜索方向,但是忽略了一些其他可能有用的信息。为了使新发生的成功跳出动作所提供的信息能够持续影响接下来的搜索过程,LBGOA将搜索单元的位置迭代演进公式变成式(9):
Xi=m×Si+(1-p)×Td+p×Xi
(9)
其中,p是用于控制搜索单元位置影响的协调参数。p在第一次迭代的时候初始化为0。如果搜索单元没有进行跳出或者跳出局部最优失败,p仍会被设置为0,以确保只有Si和Td才能影响下一次迭代演进。当搜索单元完成一次成功跳出时,p被设置为在接下来的3次迭代中线性递减为0的变量,以使成功跳出的行为对搜索过程的影响持续到接下来的3次迭代过程中。经过一些试验,p的递减间隔被设置为0.35。对p取值的进一步研究不在本文讨论范围内。参数p的计算方法如式(10):

(10)
2.3 基于Levy飞行的改进蝗虫算法流程
基于Levy飞行的改进蝗虫优化算法的搜索过程分为初始化阶段、迭代演进阶段、适应度值更新阶段和跳出阶段这4个阶段。在初始化阶段,设置参数,并随机初始化所有搜索单元的初始位置。在这一阶段中,还计算了最优目标的位置和相应的最优适应度值。在迭代演进阶段,搜索循环开始进行。每个搜索单元都通过公式(9)移动到新的位置。之后每个搜索单元根据公式(6)以一定的概率进行Levy飞行调整,并生成新的搜索位置。在适应度值更新阶段,计算新位置的适应度值。如果新的适应度值优于当前的全局最优适应度值,则新的位置可以取代旧的全局最优目标的位置。如果新的适应度值没有比当前全局最优目标的适应度值更优,那么该搜索单元就会进入跳出阶段。在此阶段,搜索单元尝试根据公式(8)跳出局部最优,并计算新的适应度值。如果新的适应度值优于当前搜索单元本身的适应度值,那么新的位置可以取代旧的搜索单元的位置,完成一次成功的跳出。此时参数p也根据公式(10)进行更新。如果新的适应度值没有优于当前搜索单元本身的适应度值,那么搜索单元不会跳到新的位置上,会仍然停留在旧的位置上。到目前为止,循环求解过程中的一次迭代已经完成。在达到最大迭代次数之后,循环过程结束,此时的全局最优适应度值和全局最优目标位置就是最终的寻优求解的结果。基于Levy飞行的改进蝗虫优化算法的流程如算法1所示。
算法1基于Levy飞行的改进蝗虫优化算法
1:初始化蝗虫集群初始位置,计算目标适应度
2:while未达到最大迭代次数do
3:根据公式(9)更新Xi的位置
4:Xi搜索单元根据公式(6)进行Levy飞行
5:计算适应度值
6:if当前适应度值优于目标适应度值then
7:更新目标适应度值和目标最优解位置
8:else
9:Xi搜索单元根据公式(9)进行跳出
10:计算适应度值
11:if当前适应度值优于搜索单元自身适应度值then
12:更新搜索单元的位置
13:end if
14:根据公式(10)设置参数p的值
15:end if
16:end while
17:返回得到的目标最优值和目标最优解的位置
3 实验结果及分析
3.1 CEC测试实验设置
为了评估所提出的基于Levy飞行的改进蝗虫优化算法(LBGOA)的性能,本文进行CEC测试实验。将LBGOA算法与6个元启发式算法的性能进行了比较,对比算法包括原始的蝗虫优化算法(GOA),基于反向学习的蝗虫优化算法(OBLGOA),最近几年新提出的3种元启发式算法:鲸鱼优化算法(WOA)、蜻蜓优化算法(DA)和蚁狮优化算法(ALO),以及经典的启发式算法粒子群优化算法(PSO)。
本文的CEC测试实验使用了CEC2014中的30个测试函数,来测试所提出的LBGOA算法的搜索性能。测试函数可以分为4种类型,用来评估算法的不同方面的性能。其中,测试函数F1~F3是单峰测试函数(Unimodal Functions),只有一个局部最优位置,可以用来评价算法的局部搜索能力和搜索的精确程度。测试函数F4~F16是具有多个局部最优的简单多峰测试函数(Simple Multimodal Functions),可以用来评价算法的摆脱局部最优能力[1]。测试函数F17~F22是混合函数(Hybrid Function),测试函数F23~F30是复合函数(Composition Functions),这2类测试函数比较复杂,在测试优化算法的搜索性能方面更具有说服力。本实验中的F1~F30等30个测试函数的维度均调整为10维,每个维度的搜索范围为[-100,100]。
使用Matlab代码完成CEC测试实验。每个算法使用30个搜索单元进行搜索,每次实验进行500次迭代搜索。为了降低意外情况对于实验结果准确性的影响,测试实验对每个算法重复30次,通过计算实验结果的统计平均值来评价算法的性能。
3.2 实验结果
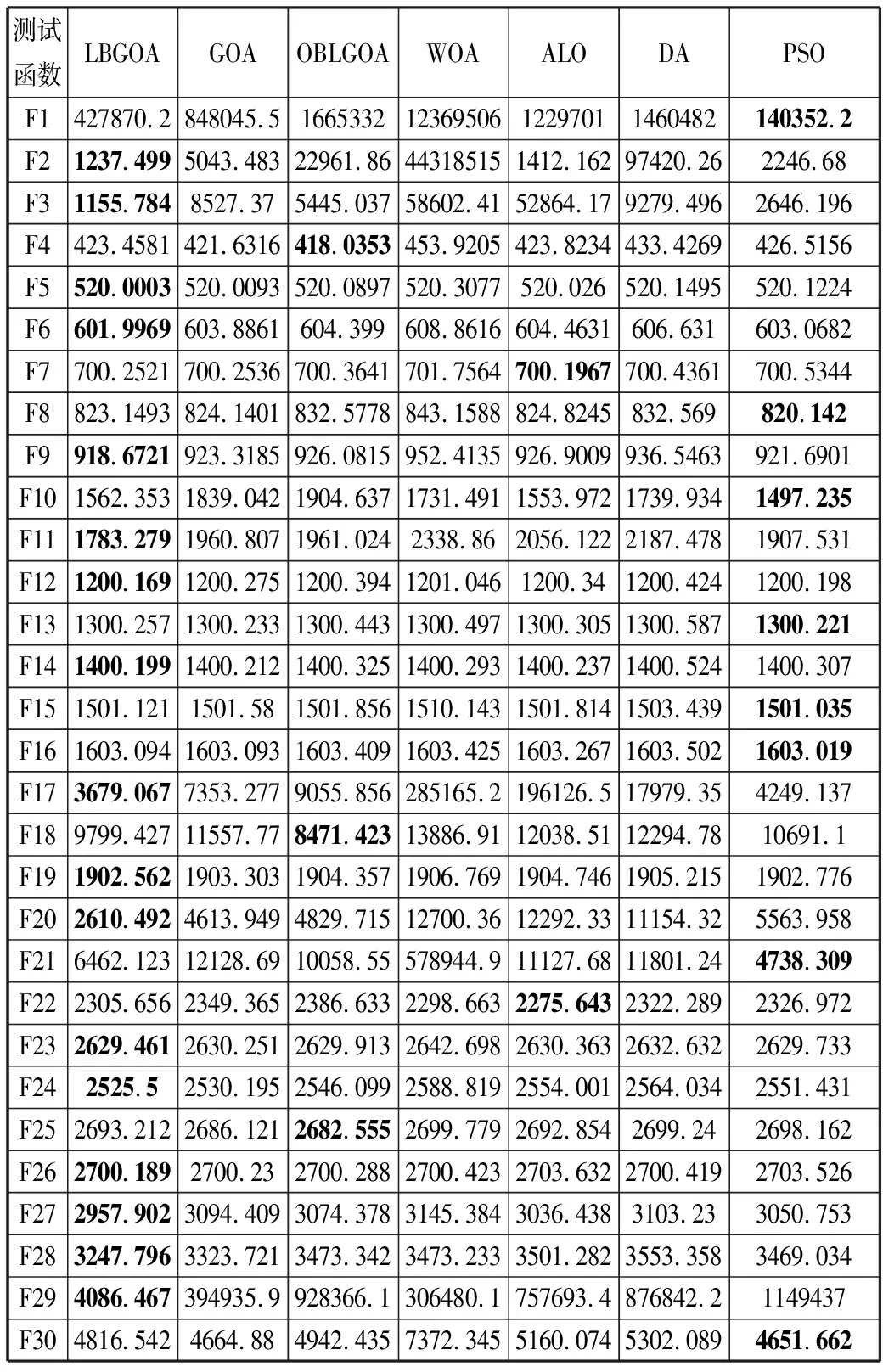
7种算法在30个测试函数上运行30次,得到的最优目标适应度值的平均值如表1所示。
表1 7种算法测试结果适应度值的平均值
测试函数LBGOAGOAOBLGOAWOAALODAPSOF1427870.2848045.516653321236950612297011460482140352.2F21237.4995043.48322961.86443185151412.16297420.262246.68F31155.7848527.375445.03758602.4152864.179279.4962646.196F4423.4581421.6316418.0353453.9205423.8234433.4269426.5156F5520.0003520.0093520.0897520.3077520.026520.1495520.1224F6601.9969603.8861604.399608.8616604.4631606.631603.0682F7700.2521700.2536700.3641701.7564700.1967700.4361700.5344F8823.1493824.1401832.5778843.1588824.8245832.569820.142F9918.6721923.3185926.0815952.4135926.9009936.5463921.6901F101562.3531839.0421904.6371731.4911553.9721739.9341497.235F111783.2791960.8071961.0242338.862056.1222187.4781907.531F121200.1691200.2751200.3941201.0461200.341200.4241200.198F131300.2571300.2331300.4431300.4971300.3051300.5871300.221F141400.1991400.2121400.3251400.2931400.2371400.5241400.307F151501.1211501.581501.8561510.1431501.8141503.4391501.035F161603.0941603.0931603.4091603.4251603.2671603.5021603.019F173679.0677353.2779055.856285165.2196126.517979.354249.137F189799.42711557.778471.42313886.9112038.5112294.7810691.1F191902.5621903.3031904.3571906.7691904.7461905.2151902.776F202610.4924613.9494829.71512700.3612292.3311154.325563.958F216462.12312128.6910058.55578944.911127.6811801.244738.309F222305.6562349.3652386.6332298.6632275.6432322.2892326.972F232629.4612630.2512629.9132642.6982630.3632632.6322629.733F242525.52530.1952546.0992588.8192554.0012564.0342551.431F252693.2122686.1212682.5552699.7792692.8542699.242698.162F262700.1892700.232700.2882700.4232703.6322700.4192703.526F272957.9023094.4093074.3783145.3843036.4383103.233050.753F283247.7963323.7213473.3423473.2333501.2823553.3583469.034F294086.467394935.9928366.1306480.1757693.4876842.21149437F304816.5424664.884942.4357372.3455160.0745302.0894651.662
从表1中可以看出,所提出的LBGOA在17个函数的测试中能够得到最优的平均适应度值,在F1、F7、F8、F15、F18和F21等6个函数的测试中能够得到次优的平均适应度值,只有在其他7个函数的测试中得到相对不够优秀的平均适应度值。
F1~F3的3个单峰函数测试结果表明,在基于Levy飞行的局部搜索机制的帮助下,所提出的LBGOA算法拥有较好的局部搜索能力,能够搜索到更精细的局部最优解。F4~F16的13个多峰函数测试结果表明,在基于线性递减参数的随机跳出策略的帮助下,所提出的LBGOA算法拥有较好的跳出局部最优困境的能力。
为了消除实验数据的偶然性并表明实验结果的显著性,本研究引入了威尔科克森秩和检验。这里计算了关于LBGOA与每个其他算法之间在测试函数F1~F30上的统计数据的p值。当p小于0.05时,可以认为2个样本之间的差异是显著的。LBGOA的威尔科克森秩和检验结果如表2所示。
表2 LBGOA算法与其他6种算法在CEC测试集上的威尔科克森秩和检验结果P值

测试函数GOAOBLGOAWOAALODAPSOF10.0050845.86E-063.02E-110.0020525.19E-073.82E-09F20.0001253.69E-113.02E-110.0579291.78E-100.297272F31.46E-104.98E-113.02E-113.02E-111.78E-100.297272F40.0446410.8883032.43E-050.0080720.0241570.033934F50.1023263.02E-113.02E-110.0099413.02E-112.03E-09F60.0001414.42E-063.02E-113.81E-078.99E-110.021506F70.0073930.0079593.02E-110.0797821.86E-060.003339F80.0099410.0003993.81E-070.0085330.0002840.018087F90.0850.002381.46E-100.0103152.32E-060.025186F100.0011748.88E-060.0198830.0088830.0467560.039526F110.022360.0144121.01E-080.0002391.02E-050.085F120.0260770.0001116.07E-110.000772.68E-060.021701F130.0080720.0002254.11E-070.0724466.53E-080.053951F140.0068431.34E-056.36E-050.18097.60E-070.001114F150.0191120.0002533.02E-110.0010582.23E-090.041191F160.0088830.0018570.0008120.0933412.28E-050.055923F170.0002842.78E-076.70E-112.37E-101.64E-050.043764F180.0233980.090490.7061710.0089990.2458140.044641F190.0042263.26E-074.50E-115.46E-091.41E-090.065204F200.0001411.19E-063.16E-101.29E-091.41E-090.000284F210.0518770.2837782.03E-090.0270860.1334540.014412F220.0112280.0008120.0064140.0555460.4289630.027061F234.80E-072.87E-103.02E-111.10E-088.15E-112.84E-10F240.0162370.0006553.69E-119.51E-066.01E-080.003339F250.0555460.0050840.0001170.0036711.34E-050.022365F260.1023260.0011746.53E-080.000626.53E-070.037282F270.0338740.0048562.37E-100.0144121.19E-060.015366F280.0241573.83E-053.26E-076.77E-058.89E-101.02E-05F290.0580180.0048560.0058270.0559236.35E-050.03255F300.0090470.0098233.57E-060.0222570.0451460.042038
从表2中可以看出,在大多数的测试结果中,LBGOA与其他几种比较算法之间的p值小于0.05,仅有少部分测试结果的p值大于0.05,说明所进行的CEC实验的实验结果是显著的。
4 LBGOA应用于任务调度问题
4.1 任务调度问题描述
在边缘计算中,由于异构边缘节点的资源情况、工作负载、处理速度和任务类型的不同,将不同的任务调度到不同边缘节点上执行会产生不同的代价。边缘计算的任务调度问题中,常见的代价包括任务执行时间和节点运行开销费用[23]。
本节将所提出的LBGOA算法应用于边缘计算中的任务调度问题。将N个任务调度到M个异构节点的一种调度方案抽象为搜索空间中的一个点的位置,每一种调度方案都是一个N维离散向量[24]。每个调度方案可以对应一个任务总执行时间和节点运行开销费用,并且以此来计算任务调度问题中的适应度值。搜索单元集群通过LBGOA算法在整个搜索空间中搜索最佳适应度值的位置,能够得到最优或近似最优的任务调度方案。
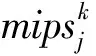
(11)
第j个节点的执行时间stj是通过将在第j个节点上执行的所有任务的执行时间相加得到的。计算方法如公式(12)所示:
(12)
总的执行时间Makespan为所有节点的执行时间取最长值。计算方法如公式(13)所示:
Makespan=max{stj|j=1,2,3,…,M}
(13)
工作节点在执行任务的时候会产生额外的开销费用。费用只与工作节点的工作时间有关,不论工作节点上执行的是什么类型的任务。节点的开销费用价格为bpsj,表示第j个节点在单位时间内产生的任务执行开销费用。总的费用Budget是通过将所有节点产生的费用相加得到的。Budget的计算方法如公式(14):
(14)
Makespan和Budget是从2个方面来描述任务调度问题的开销情况的,因此需要一个统一的评估适应度。在本文中,任务调度问题的评估适应度被定义为Makespan和Budget通过权重参数和进行结合的结果。评估适应度fitness的计算方法如公式(15):
fitness=α×Makespan+β×Budget
(15)
优化问题的搜索过程是连续的,但任务调度问题的解决方案是离散的,所以需要对LBGOA算法进行离散化处理。当每个循环迭代的过程结束后,所有的搜索单元都向距离其最近的整数位置进行调整。
4.2 任务调度问题实验设置
在此任务调度模块中,N个任务被分为K种类型,M个工作节点正在等待处理它们。在本文的工作中,不失一般性地,将K、N和M分别设置为4、10和5。为了平衡Makespan和Budget对fitness的影响,系数α和β设置为0.7和0.3。任务类型及任务消耗资源情况如表3所示。
表3 任务类型及资源消耗情况
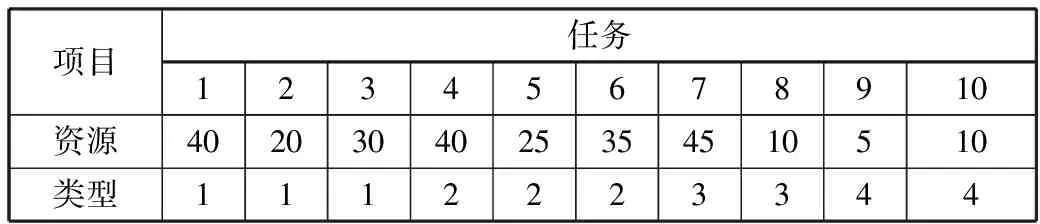
项目任务12345678910资源4020304025354510510类型1112223344
每个节点拥有的总可用资源及节点开销费用价格bps情况如表4所示。
表4 节点拥有资源及开销费用价格bps
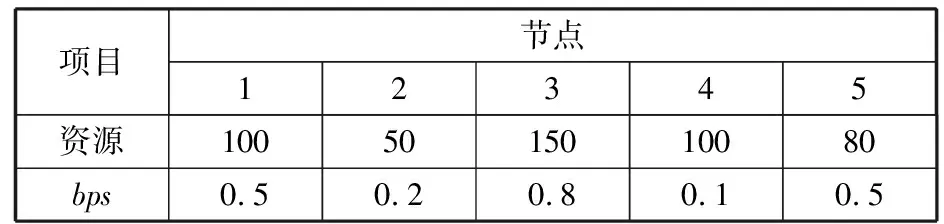
项目节点12345资源1005015010080bps0.50.20.80.10.5
表5 任务和节点的mips
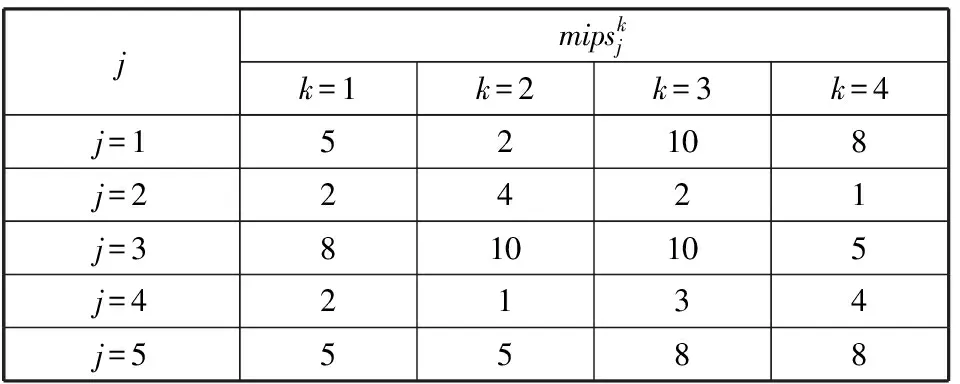
jmipskjk=1k=2k=3k=4j=152108j=22421j=3810105j=42134j=55588
本文将所提出的LBGOA算法与另外6种算法进行比较,包括GOA、OBLGOA、WOA、ALO、DA和PSO,每种算法使用30个搜索单元进行搜索。为了减少意外因素的影响,对每种算法进行30次独立测试,计算并比较测试结果的平均值(avg)、标准差(std)、最优值(min)、最差值(max)以及LBGOA相比不同算法的效果提升程度(pro)等统计数据。实验结果如表6所示。
表6 任务调度实验结果
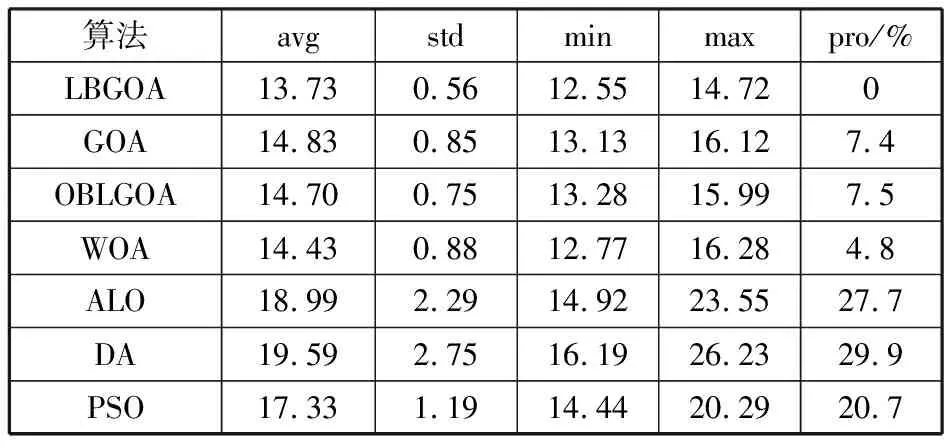
算法avgstdminmaxpro/%LBGOA13.730.5612.5514.720GOA14.830.8513.1316.127.4OBLGOA14.700.7513.2815.997.5WOA14.430.8812.7716.284.8ALO18.992.2914.9223.5527.7DA19.592.7516.1926.2329.9PSO17.331.1914.4420.2920.7
任务调度实验结果表明,本文所提出的LBGOA在所有评价指标方面都优于其他算法。在平均值方面,LBGOA能够得到最优的解决方案。相比原始GOA算法和OBLGOA算法,LBGOA算法能够将平均值效果分别提升7.4%和7.5%,这说明所提出的2种针对GOA的优化策略是有效的。相比其他4种算法,LBGOA算法能够将平均值效果分别提升4.8%、27.7%、29.9%和20.7%。另外LBGOA拥有最小的标准差,说明该算法相比其他算法更加稳定。LBGOA可以找到所有算法中的最优解,并且找到最差解的值相比其他算法找到的最差解也更优。综上所述,本文所提出的LBGOA算法在解决边缘计算中的任务调度问题方面性能非常优秀,相比其他算法效果提升非常显著。
5 结束语
本文针对蝗虫优化算法随机性差、容易陷入局部最优的问题,提出了一种基于Levy飞行的改进蝗虫优化算法(LBGOA),并将其应用于解决边缘计算中的任务调度问题。一方面该算法引入了基于Levy飞行的局部搜索机制,扩展搜索单元的搜索半径,增强算法的随机性以及局部最优值的搜索能力。另一方面,该算法采用了基于线性递减参数的随机跳出策略,增强了算法跳出局部最优的能力。实验结果表明,所提出的基于Levy飞行的改进蝗虫优化算法相比原始GOA算法及其他几种对比算法,能够获得更优的搜索精度。将所提出的LBGOA算法应用于边缘计算中的任务调度问题,实验结果表明,该算法也能够取得更优的搜索结果,相比GOA、OBLGOA、WOA、ALO、DA和PSO算法,搜索效果分别提升7.4%、7.5%、4.8%、27.7%、29.9%和20.7%。

