自卸汽车车厢纵梁强度校核分析
郑莉, 周琼
(江西交通职业技术学院 汽车工程系, 江西 南昌 330013)
自卸汽车车厢纵梁不仅承载着车厢自重和载质量,在车厢倾卸时,还受到来自举升机构的举升力作用,此时车厢纵梁的负荷较大。因此,在车厢设计前,需根据整车布置对车厢纵梁强度进行校核计算,据此选择合适的车厢纵梁截面和材料。
1 自卸汽车车厢纵梁的结构和材料
自卸汽车车厢纵梁多为平直且截面形状不变,截面形状一般有匚形(见图1)和口形(见图2)两种。匚形截面可由普通钢板机械加工而成,也可以是槽钢;口形截面为矩形钢管或方形钢管,也可由槽钢对接焊接而成。纵梁截面的形状和尺寸决定其截面系数,而纵梁材料决定其许用应力。抗弯截面系数越大,纵梁的抗弯性能越好;许用应力越大,则纵梁的安全性越高。因此,纵梁的结构和材料极为重要。
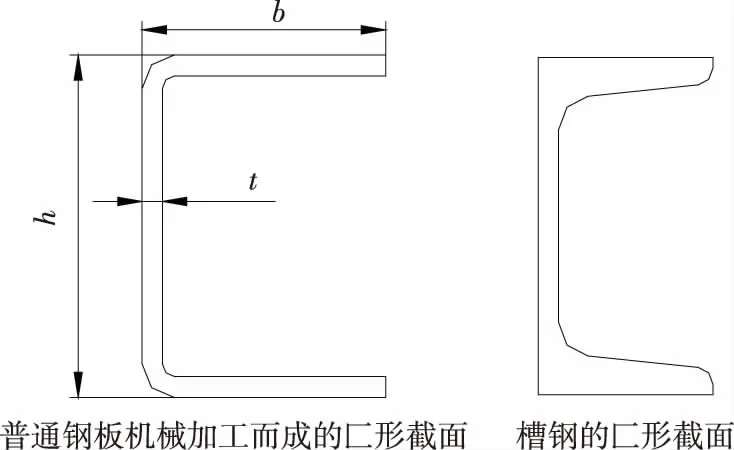
h为高度;b为腿宽度;t为腰厚度。
2 自卸汽车车厢纵梁强度的校核计算
以某公司自卸汽车为例,对车厢强度进行校核计算。
2.1 自卸车概况
该车型设计载质量为855 kg,考虑到实际使用中存在的超载现象,以2 000 kg的载质量进行校核。车厢未进行举升时,等同于非自卸车厢,车厢不受垂直方向的弯曲应力,车厢纵梁强度能满足使用要求。车厢举升过程中,车厢受到载荷G、举升机构举升力F和后翻转处的力N的作用。随着举升角度的增大,载荷G相对于后翻转点的力臂逐渐减小,而举升力F相对于后翻转点的力臂逐渐增大。根据力矩平衡原理,举升力F将随着举升角度的增大而减小。因此,车厢刚举升时,举升力F最大,车厢纵梁负荷最大,故只需对这种情况下的车厢进行强度校核计算。下面根据整车总体布置确定的举升机构方式及安装点,在载重2 000 kg(不含车厢自重200 kg)举升时对车厢纵梁强度进行分析。
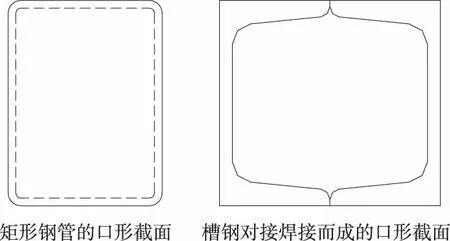
图2 自卸汽车车厢纵梁的截面形状(口形截面)
车厢纵梁受力见图3。假设车厢受货物及自身重力G作用,且均匀分布,O点为载荷质心;车厢纵梁长度L=2 510 mm,点A、B为纵梁两端点;点C为举升杆与车厢铰接点,点D为车厢后翻转点;举升杆产生举升力F,D点处对车厢形成压力N;点E为重力G与举升力F的延长线交点,ED为力N的作用方向;车厢为均匀举升。
以D点为旋转点,根据力矩平衡,有:
G×1 134.669=F×740.216

图3 车厢纵梁受力示意图(单位:mm)
F=G×1 134.669/740.216≈1.533G
以C点为旋转点,根据力矩平衡,有:
G×332.972=N×534.254
N=G×332.972/534.254≈0.623G
力F在Y方向的分力为:
FY=Fsin75°≈1.481G
力N在Y方向的分力为:
NY=FY-G=0.481G
2.2 车厢纵梁所受内力及弯矩
按G=(2 000 kg+200 kg)×9.8 N/kg=21 560 N计算。AC段长度a=1 629.661 mm,CD段长度b=801.697 mm。现以截面法求距离A点x距离的纵梁截面的内力Q和弯矩M,并分为AC、CD和DB段来计算。车厢纵梁数量为2。
在AC段,以截面左端计算,合力为零,力矩平衡,则内力为:
Q=xG/L/2=4.294 8x(0 弯矩为: M=xG/L/2×x/2=2.147 4x2(0 在CD段,以截面左端计算,合力为零,力矩平衡,则内力为: Q=-(FY-Gx/L)/2=4.294 8x-15 961.484 (a 弯矩为: M=-[FY(x-a)-Gxx/2L]/2=2.147 4x2- 15 961.484x+26 011 807.976 9 (a 在DB段,以截面右端计算,合力为零,力矩平衡,则内力为: Q=-0.5G(L-x)/L=4.298 4x-10 780 (a+b 弯矩为: M=-0.5G(L-x)(L-x)/2L=-2.147 4x2+ 10 780x-13 528 900 (a+b 根据以上计算结果,车厢纵梁所受内力及弯矩分别见图4、图5。 图4 车厢纵梁所受内力 图5 车厢纵梁所受弯矩 由图4、图5可知:在C点处,车厢纵梁所受内力及弯矩均最大。 纵梁所受最大弯曲应力δmax=Mmax/WZ(WZ为车厢纵梁的抗弯截面系数)。对于由普通钢板机械加工而成的匚形截面,WZ为: WZ=(h+6b)th/6 以2 400 mm轴距平板车厢纵梁尺寸计算: WZ=(h+6b)th/6=(50+6×55)×2× 50/6=38 000/6 mm3 Mmax=5 703 081.639 35 N·mm,则: δmax=Mmax/WZ=900.486 6 N/mm2 该纵梁材料为Q235薄钢板,屈服强度δs=235 MPa<δmax,该纵梁用于自卸汽车车厢,在举升时会断裂。若仍使用该结构,在h和b不变的情况下,厚度t至少需增至t=2δmax/δs=900.486 6×2/235≈7.7 mm,从成本上考虑该结构不适用。 如果纵梁材料换为Q235的8#槽钢,根据GB/T 707-1988《热轧槽钢尺寸、外形、重量及允许偏差》,其截面模量Wx=25 300 mm3,则: δmax=Mmax/Wx=5 703 081.639 35/25 300= 225.418 N/mm2<δs=235 MPa 8#槽钢能满足使用要求。但考虑到δmax较接近δs,且实际举升过程并非均匀举升,δmax的实际值比计算值大,出于安全考虑,不宜采用8#槽钢制作该自卸汽车车厢纵梁。 如果纵梁材料换为Q235的10#槽钢,根据GB/T 707-1988,Wx=39 700 mm3,则: δmax=Mmax/Wx=5 703 081.639 35/39 700= 143.654 4 N/mm2<δs=235 MPa 10#槽钢能满足使用要求,可用作该自卸汽车车厢纵梁。 若纵梁材料换为Q235的(80×60×4) mm矩形钢管,根据GB/T 3094-2000《冷拔异型钢管》,其截面模量Wy=23 190 mm3,则: δmax=Mmax/Wy=5 703 081.639 35/23 190= 245.928 5 N/mm2>δs=235 MPa (80×60×4) mm矩形钢管不能满足使用要求,在车厢举升时纵梁会断裂。 若纵梁材料换为Q235的(80×60×5) mm矩形钢管,查GB/T 3094-2000,Wy=27 680 mm3,则: δmax=Mmax/Wy=5 703 081.639 35/27 680= 206.036 N/mm2<δs=235 MPa (80×60×4) mm矩形钢管能满足使用要求,可用作该自卸汽车车厢纵梁。 根据以上计算分析结果,10#槽钢和(80×60×5) mm矩形钢管都能满足使用要求。在实际生产制造过程中,从材料成本及备料方面考虑,该车型车厢纵梁最终采用10#槽钢来制作。 上述车厢纵梁校核计算方法是最基本的一种,其他不同结构、材料的自卸汽车车厢纵梁可参照该方法进行校核计算。该车型已通过两轮试装验证及可靠性试验,结果表明,车厢的强度能满足整车承载要求,与校核计算结论吻合。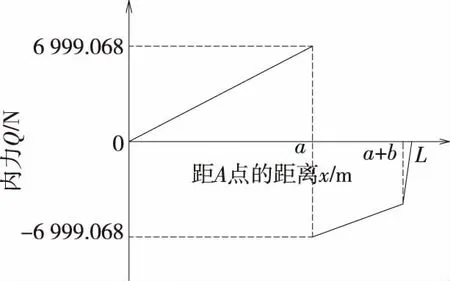

2.3 车厢纵梁强度校核
3 结语

