应变天平测量电路退化及失效检测技术*
王南天,许晓斌,马晓宇,王 雄,童 帅
(中国空气动力研究与发展中心, 四川 绵阳 621000)
风洞天平是风洞测力试验最基础、最重要的测量设备,一直倍受重视[1-2],其中应变天平作为常规测力试验的主要测量设备之一,被广泛应用于各类风洞特别是高超声速风洞的测力试验中。典型应变天平的核心是弹性梁与测量梁变形的惠斯登电桥[3-5]。在高超声速风洞测力试验中,风洞启动时的高温高压气流冲击会使模型发生较大的振动,气流的不稳定等因素也可能引起模型振动,这些都可能引起模型内天平测量电路的退化或者失效,影响天平使用。
目前,当天平数据发生异常时,一般由“老师傅”手动检测电桥各点位的电压,依据经验对故障进行分析诊断,这将花费较多的时间,而且没有发现针对此问题的文献。为此,本文引入自动测试技术,通过不同时刻在电桥不同节点施加激励并测量响应,基于理论模型分析电桥的特征参数,引入聚类的方法对测量电路进行失效检测,并研制相应的退化及失效检测系统,以节省其故障诊断时间,提高风洞试验的可用时间,以更好地保证风洞试验任务的完成。
1 检测方法建模
1.1 应变天平基本原理
应变天平的基本原理是通过测量外力引起的变形,来测量输入的外力和力矩。应变天平一般包含多个测量通道,每个天平的测量通道数不一定相同且通道间测量结果之间的耦合也不相同,单个通道的基本测量结构一致,为惠斯登电桥,如图1所示。
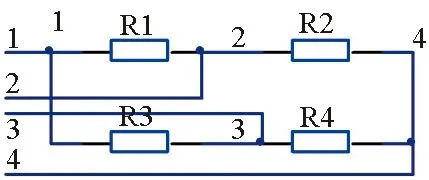
图1 天平测量电路基本结构Fig.1 Structure of the balance′s measuring circuit
当天平有力输入时,会引起天平的机械本体的应变,进而引起与其固连的应变片的电阻值R1发生ΔR1的变化。当在节点1与4之间输入一个电压时,R1的变化引起节点2、3之间的电压(如式(1)所示)发生变化。由于ΔR1≪R1,对两边求导并作线性处理,可得到式(2):ΔU23与ΔR1呈线性关系,故在节点1、4间电压稳定的情况下,可通过测量ΔU23得到表征天平应变量的ΔR1,再通过耦合公式,解析出各个分量的力和力矩。由于电路的对称性,如果使用电阻R2作为测量电阻,则可以去掉式(2)中增益系数的负号,将增益改为正。
在工程上,一般取R1与R2(R3与R4)为相同阻值、同一批次的电阻,且安装在温度几乎一致的环境,这样温度变化将引起相同的电阻变化,从而抵消掉零位漂移,式(2)可简化为式(3)。由式(3)可以看出,电阻的零位阻值变化R1将引起增益的变化;此外U14的变化也将引起测量增益的变化,在模数转化时,用U14作为参考电压理论上可以抵消该影响。
(1)
(2)
(3)
1.2 检测电路失效模式与检测模型
长期的风洞试验表明,应变天平可能发生的退化和失效模式主要包括零点漂移、增益变化、开路、短路、虚焊等。随着天平使用时间的增加,加之天平处于温度应变的工作环境,受到热的影响,其总应变片可能发生退化而导致其电阻变化,这将主要引起天平零点的漂移,也会引起天平增益的变化。由于应变片的松动,相同天平机械应变引起的应变片电阻变化减小,会使天平的增益减小。由于外力拉动、挤压等原因,天平应变片的焊点甚至导线本身可能会出现断开的情况,发生开路故障。天平应变片引线焊点的虚焊,可能引起间歇性的电阻增加或者开路。此外,测量电路和模型短路的情况也可能发生。
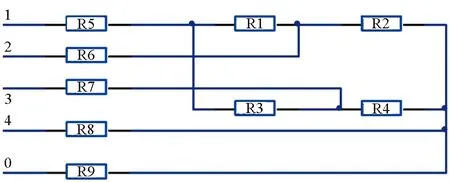
图2 天平测量电路故障检测电路模型Fig.2 Failure detection model of balance′s measuring circuit
针对上述可能的故障失效模式,建立如图2所示失效检测电路模型:电阻R1~R4为电桥本身的电阻,R5~R8为引出的4条线的线电阻,R9为测量电路与大地(天平本体)的隔离电阻。一般情况下,R1~R4为百欧姆量级,R5~R8的大小与线缆的长度等有关,常用的AWG30铜线电阻约为0.34 Ω/m,R9一般可认为为无穷大。
该模型对外有5个输入输出节点,与物理结构相符:节点0对天平本体,通过依次连接的支杆—攻角机构—风洞本体与大地连接,节点1~4分别对应电桥的4条引线端点。基于电路对称结构,为下文论述方便,如无特殊说明,假定R1为测量应变片,R2为温度补偿电阻,R3和R4为另一桥臂。表1给出了不同退化或者失效在模型中的表现形式。
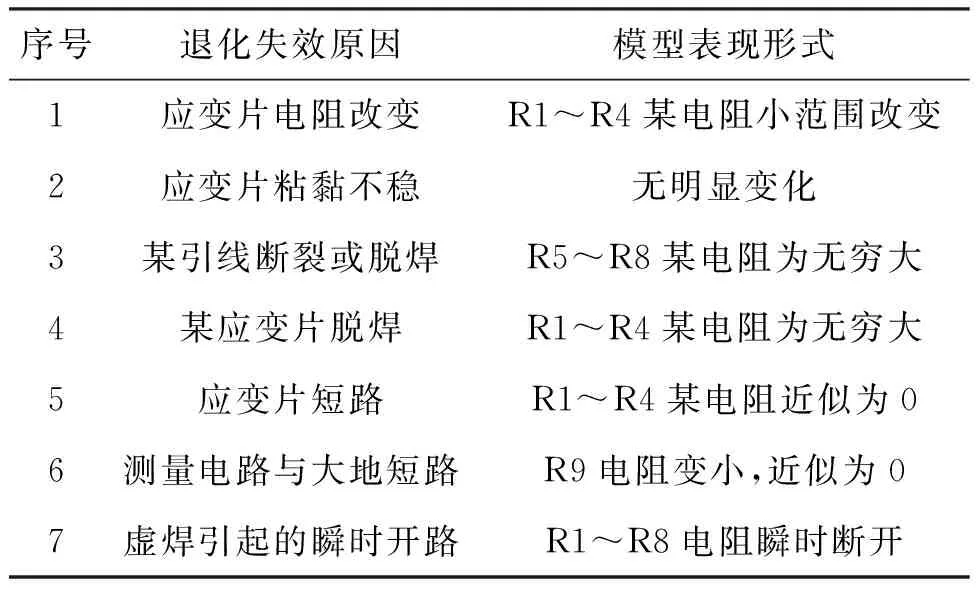
表1 退化或者失效在模型中的表现形式
1.3 失效检测模型
退化或者开路断路等永久性故障,表现形式为模型中静态指标的变化,即电阻的变化,表1也可表明此。本检测方法针对此类故障,其本质是电阻的测量与聚类。
由于该模型只有5个输出节点,要估计9个模型参数比较困难。在实际应用中,由于电桥的4条导线一般长度相同且选用同样的型号,因此假设4条导线的电阻相等,即:
R5=R6=R7=R8
(4)
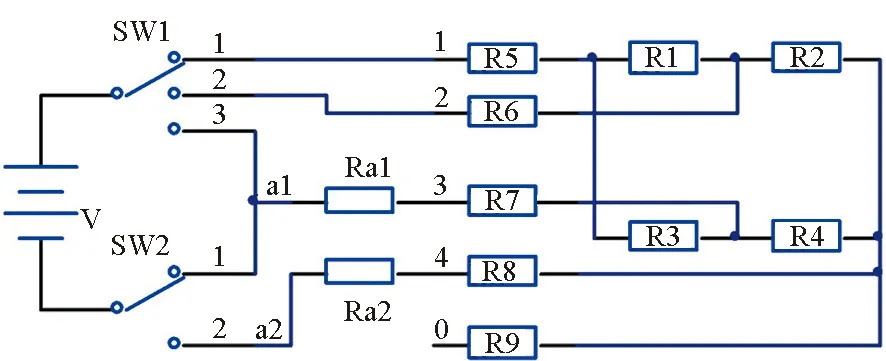
图3 退化与开路短路失效检测原理Fig.3 Detecting principle of circuit degradation or open/short circuit failure
采用图3所示基本原理对测量电路进行检测:将开关SW1和SW2连接到不同位置,分别在电桥的节点1或2与节点3或4之间施加激励,并测量节点0~4、a1和a2这7个节点之间的电压差,通过解算得到各参数。图中V为电源,Ra1和Ra2为高精度低温漂参考电阻。
首先在节点1与4之间添加电压,设电流为I14,基于基尔霍夫定律可以得到:
(5)
U4a2=Ra2I14
(6)
其中,
(7)
联立式(5)~(7)可以得到:
(8)
与式(8)类似,在节点2与4之间加电流可以得到:
(9)
(10)
在节点3与4之间加电流可以得到:
(11)
在节点2与3之间加电流可以得到:
(12)
方程(8)~(12)中,其右侧的电压比可以通过模数转换器(Analog-to-Digital Converter, ADC)测量得到,且Ra1和Ra2为已知的高精度低温漂电阻,电阻值Ra1、Ra2已知,即可以通过联系方程(8)~(12)和假设条件方程(4)得到R1~R8。
基于精确测量的R1~R8可以对天平进行退化分析。针对模型中电阻R1~R8中某电阻发生开路,R1~R4、R9某电阻发生短路,可基于理论分析的方式得到各种失效模式下的测量值,通过测量值聚类的方式进行失效分析。一般情况下,单故障发生概率相对较高,考虑到多故障同时发生将有特别多的故障表现形式且发生概率很小,因此本方法暂时针对单故障。
2 检测样机研制
为使样机简洁灵活,采用“前端测量装置+计算机软件”的结构:基于前端测量装置进行原始数据采集,保证采样数据的精确方便;基于计算机软件进行数据分析,可以在不改变前端的基础上升级检测方法,增加设计的灵活性。
2.1 前端测量装置
ADS1263是TI公司的32位高精度ADC[6],支持11个模拟量引脚,它们不仅可作为ADC转换差分输入或者参考电源输入,还可以用于电流源输出和作为通用输入输出(General-Purpose Input/Output, GPIO)。这些特征使该芯片特别适合于本样机的前端采集电路设计。
基于ADS1263设计的前端测量装置结构如图4所示:采用ADS1263+单片机的基本结构。ADS1263是采集的核心部分,某个INx(如图中红色长虚线)作为电流输出驱动电桥(电桥通过连接器节点①②③④接入样机),另一个INx(如图中蓝色短虚线)设置为GPIO输出,并输出低电平作为电流源的回流通路,剩余的INx作为差分输出,用于测量需要检测的电压,如U2a2、U3a2、U13等。单片机则提供ADS1263与上位机软件的通信接口。
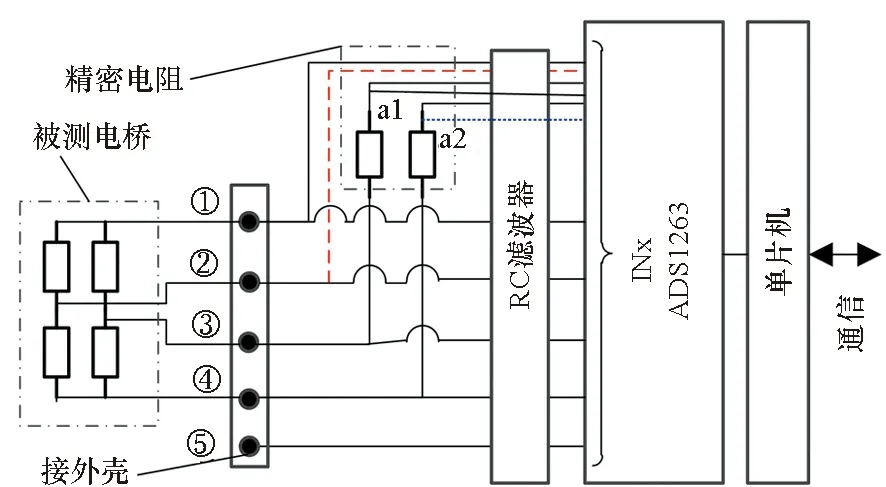
图4 前端测量装置原理示意Fig.4 Schematic diagram of front-end measuring system
2.2 上位机软件
上位机软件的主要任务是基于式(4)和式(8)~ (12)实现电阻R1~R8的求解。考虑本系统为样机,需要后期改进升级的地方较多,而MATLAB是工程计算中十分常用的软件,故选用MATLAB作上位机软件。
软件具有仿真模式和测试模式。仿真模式基于MATLAB Simulink,需要的电压数据从Simulink获取,用于算法的仿真与验证。测试模式则使用前端采集电路获取电压数据,用于天平测量电路退化与失效检测。软件还支持将天平检测电路的测量数据按照天平名称和通道进行后台存储,并包含时间戳,用于对天平的整个退化过程进行监控、分析等。
图5给出了上位机软件的主界面。图中数字为仿真结果,仿真的输入电阻为R1=350 Ω,R2=351 Ω,R3=352 Ω,R4=353 Ω,R5=R6=R7=R8=1 Ω,R9=Inf(无穷大)。
仿真结果与输入的真实值相同,表明该方法对R1~R8的估计理论上是无偏的。
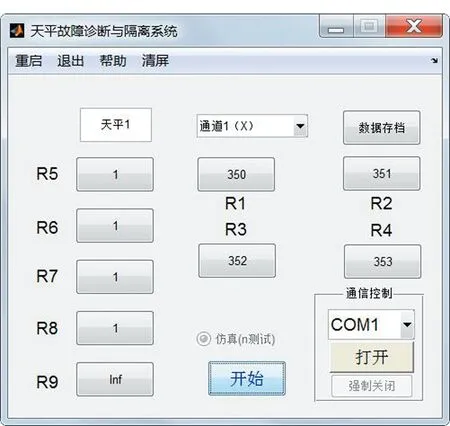
图5 上位机软件主界面Fig.5 Main interface of the upper computer software
3 实验与应用
3.1 功能测试
图6给出了实现本检测方法的原理样机的前端检测电路(图中上方)和电桥模拟电路(图中下方),电桥模拟电路可以设置模型中的R1~R8为无穷大、近似为0或者百欧姆范围内调整,设置R9近似为0 Ω。

图6 前端测量电路与被测电桥Fig.6 Hardware of front-end measuring circuit and tested bridge
1)调整R1~R4,用该原样测试结果,可以检测到相应电阻变化。图7(a)为其中一次检测结果。
2)设置R1~R8为无穷大(相应支路的开关断开),可以检测到相应的开路故障。图7(b)为其中一次检测结果,图中“Inf”表示断开。
3)设置R1~R4或R9为0(相应支路的开关闭合),可以检测到相应的故障。图7(c)为其中一次检测结果,图中“0”表示短路。
测试结果表明,该系统具备R1~R8的阻值测量与开路测量能力、R1~R4以及R9的短路测量能力,即本样机具备检测表1中的第1项和第3~6项对应的退化或者失效。
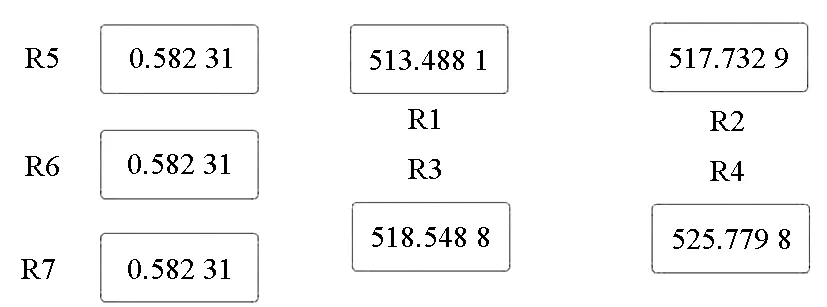
(a) 电阻变化(a) Resistance change
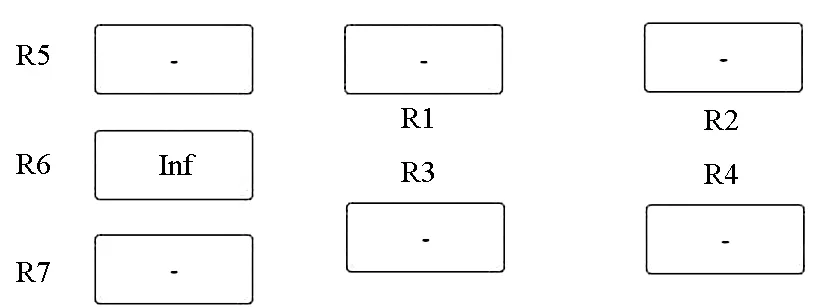
(b) R6断开(b) R6 open-circuit
(c) R2短路(c) R2 short-circuit图7 试验测试结果Fig.7 Results of experiment
3.2 精度测试
用4个25 ppm的300 Ω的精密电阻组成电桥,连接到原理样机进行精度测试。
表2给出了20次的测试结果,表3给出了表2中数据的统计结果,其中ave为平均值,Δmax(Δmin)为其中最大(小)值与平均值的差的绝对值,err_max(err_min)为Δmax(Δmin)与ave的比值。
从测试结果看,该样机测量电桥电阻为300 Ω,桥臂电阻R1~R4的电阻值测量最大误差约为0.113‰(表3中下划线数值)。由式(3)可知由此测量可能带来的增益误差最大为4×0.113‰≈0.46‰。由于导线电阻本身较小,测量的误差较大,最大约为10 mΩ。由于导线采用的是弹簧压接的方式,模型中的导线电阻实际是导线电阻和接触电阻,因此不同的测试之间可能存在小的变动,这可能是导致测量结果有较大偏差的一个原因。
4 结论
针对应变天平检测电路失效快速检测的需求,研究了电桥的退化与失效自检测方法,仿真结果表明该电阻估计方法理论无偏;设计了原理样机,实验结果表明该方法有效,电桥电阻测量精度可达0.2‰,导线电阻测量精度约为2%。该方法可以为电桥的退化分析与故障诊断提供支持,实现应变天平检测电路的故障自动检测,节省故障诊断时间,提高风洞试验可用时间。下一步将研究提高测量精度的装置。
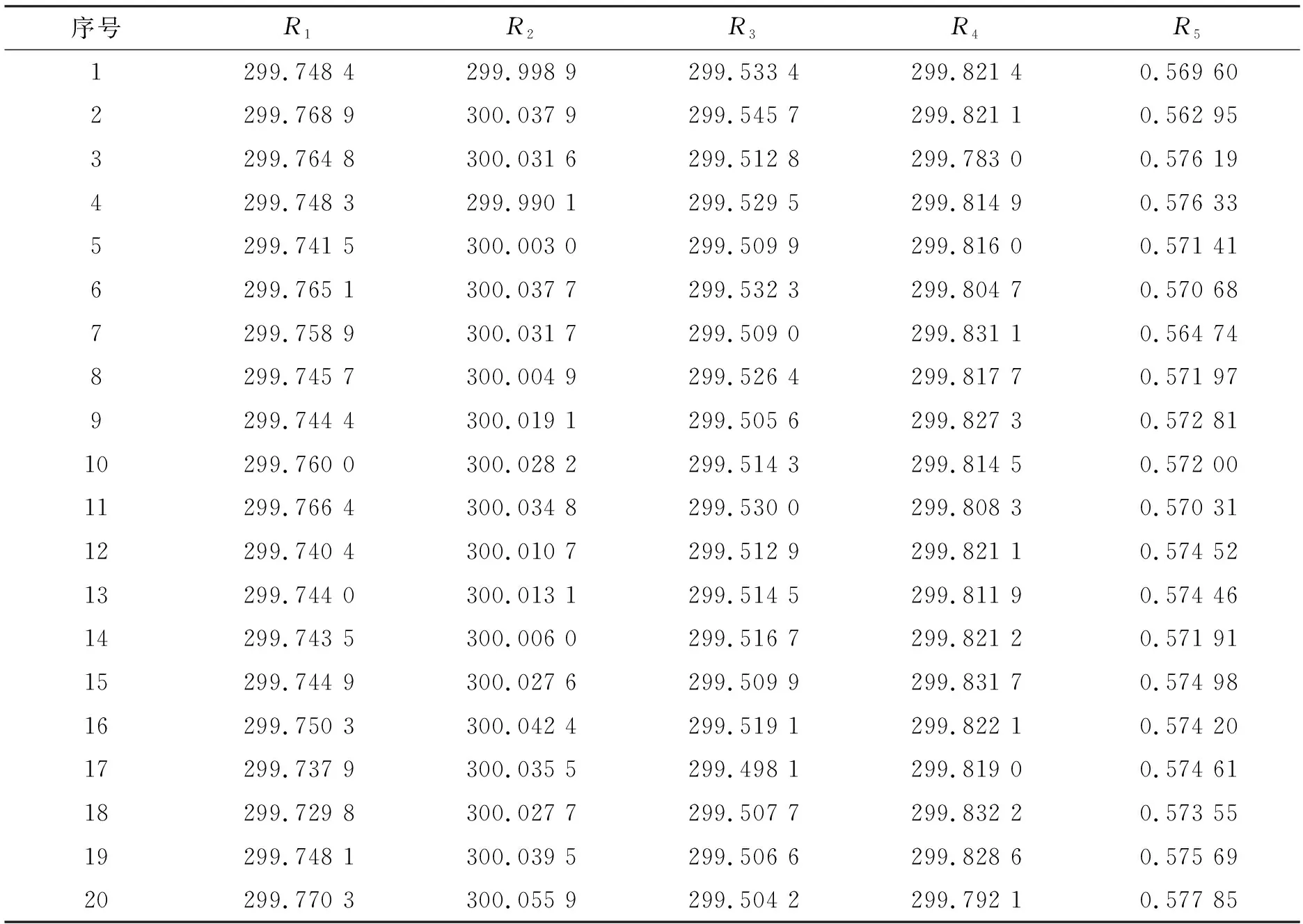
表2 20次测量结果
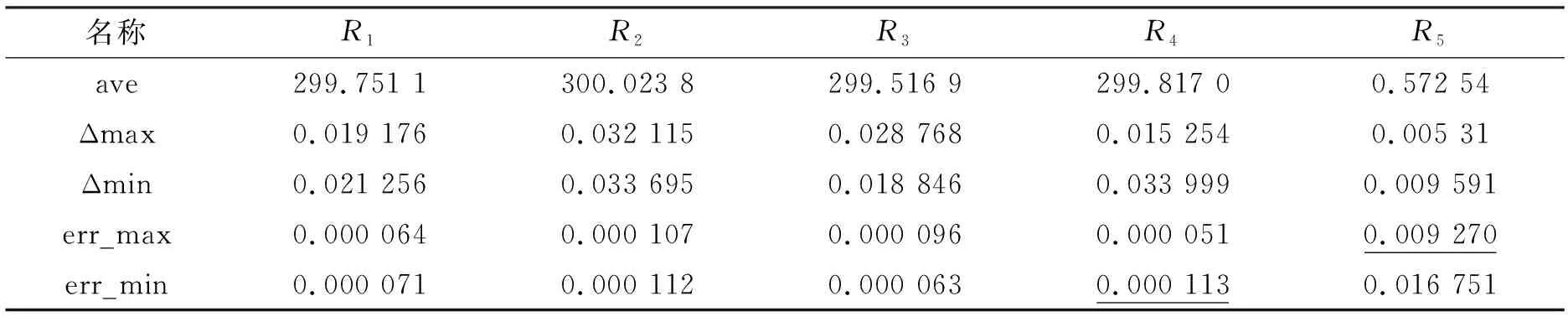
表3 统计结果

