滑翔飞行器多目标弹道优化的进化-配点混合求解策略*

丰志伟，江增荣，张青斌，葛健全，黄 浩

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2.中国人民解放军96901部队， 北京 100094)

高超声速滑翔飞行器(Hypersonic Glider Vehicle，HGV)具有高速度、高机动、长航程等诸多优势，成为未来飞行器发展的一个重要方向，具有广阔的军事应用前景[1]。

弹道优化技术是高超声速滑翔飞行器的关键技术之一。随着研究的不断深入，在进行高超声速滑翔飞行器弹道设计之中，不仅要考虑飞行器在飞行过程中受到的气动热、动压、过载、控制量、终端约束等复杂约束条件的限制，还需要考虑面向具体作战任务的要求，如航路点、禁飞区等。面对诸多性能指标，设计者往往不能追求单个指标最优，而是需要同时考虑多个相关的性能指标，利用多目标优化方法进行求解，获得Pareto最优解，从而对各个指标进行权衡和折中[2]。

对于高超声速滑翔飞行器的多目标弹道优化问题而言，工程上常用的方法是利用偏好(权重)信息，将多个目标聚合为单个目标，并采用成熟的单目标优化算法进行求解。主要优化方法包括加权法、理想点法、物理规划法、主要目标法等[3]。雍恩米等[4]应用物理规划法设计再入飞行最优攻角；谢愈等[2]将物理规划法应用于高超声速飞行器多目标复杂约束滑翔弹道优化设计，结合高斯伪谱法获得了满足设计者偏好的满意解。上述基于偏好的方法每次只能优化得到一个解，无法得到整个Pareto前沿(Pareto Front, PF)。为了获得多个Pareto最优解(Pareto Set, PS)，通常需要采用多目标优化方法来进行设计。主要优化方法包括各种多目标进化算法、多目标粒子群算法等[5]。例如，陈刚、王明光等[6-7]将多目标遗传算法NSGA-II成功应用于可重复使用运载火箭最优再入弹道优化设计；丰志伟等[8]应用分解多目标进化算法(Multiobjective Optimization Evolutionary Algorithm based on Decomposition, MOEA/D)求解火星再入飞行器一体化多目标优化设计问题。

滑翔飞行器弹道优化问题是一个带有复杂约束的最优控制问题，本文综合考虑计算效率和精度，提出一种结合进化算法和配点法的混合、分层多目标优化策略。为了获得具有较高精度的全局最优解，将多目标弹道优化问题的求解分为两步：①使用较少节点对弹道优化问题进行离散化处理，采用MOEA/D进行多目标优化计算，获得Pareto前沿和全局最优解集；②以多目标最优解作为基于二代小波节点自适应配点法[9]的初始解进行精细优化，获得较高精度的弹道。特别是，在MOEA/D和自适应配点法中采用了椭球聚合法[10]将多个目标函数聚合为单个目标函数。

1 滑翔飞行器多目标弹道优化模型

1.1 再入动力学方程

以地心距r、经度λ和纬度φ描述飞行器位置，以速度大小V、速度倾角θ和速度偏角σ描述飞行器速度，建立的滑翔飞行器三自由度运动方程[11]可表示为

(1)

其中：X为阻力，Y为升力，L为侧向力，m为飞行器质量，g为引力加速度；速度倾角θ为速度矢量与当地水平面的夹角，速度偏角σ为速度矢量在当地水平面投影与正北方向的夹角；ωe为地球自转角速度，ν为侧倾角。由于滑翔飞行器为面对称升力体，通常采用倾斜转弯(Bank To Turn, BTT)技术，在上述运动方程中假设侧滑角为零。

1.2 约束条件分析

滑翔飞行器多目标弹道设计约束条件[12]包括：热流、动压、过载、平衡滑翔、禁飞区、航路点等过程约束；弹道末端需满足的终端状态约束；对攻角、侧倾角的控制量约束。

1)气动热、过载和动压约束：为了保证飞行器结构安全，对沿弹道飞行的热流密度、动压、过载等进行限制。

驻点热流密度约束为

(2)

过载约束为

(3)

式中，α为攻角。

动压约束为

(4)

2)拟平衡滑翔约束：为保证弹道平稳，沿弹道飞行器可获得的最大升力须能够平衡其他力，即

(5)

3)禁飞区约束：禁飞区指飞行需要规避的区域，包括躲避雷达探测等。为便于计算，假设禁飞区为无限高圆柱，弹道点与禁飞区中心在地面投影的最短距离满足如下约束

|R0·arccos[sinφsinφnfz+

cosφcosφnfzcos(λ-λnfz)]|>Rnfz

(6)

其中，λnfz和φnfz分别表示禁飞区中心经纬度，Rnfz表示禁飞区半径。

4)控制量约束：由于受执行机构能力限制，攻角、侧倾角等物理量的幅值存在约束边界

(7)

5)终端约束：本文主要开展最大射程优化，不约束滑翔段终点的位置和速度。

1.3 性能指标

按照飞行任务的不同，可选择不同的性能指标。常用的优化目标有终端射程最大、飞行时间最短、总加热量最小等。如取终端射程最大为优化指标，则

J=min[-L(tf)]

(8)

当选择总加热量最小作为性能指标时，则

(9)

2 多目标优化问题的混合求解策略

多目标弹道优化问题的核心是获得一组较为精确的Pareto全局最优解集。为此，本文提出结合分解多目标进化算法和配点法的混合求解策略。为了保证两种多目标优化方法求解问题的一致性，均采用椭球聚合法[10]将多目标优化问题转化为单目标优化问题。

2.1 混合求解策略

混合求解策略优化流程如图1所示。具体计算过程如下：

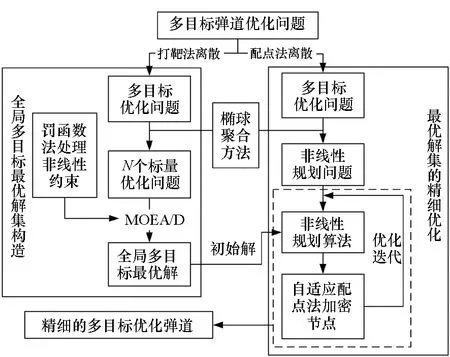
图1 混合求解策略流程图Fig.1 Flow chart of hybrid optimization strategy

1)定义多目标弹道优化问题：定义状态方程，确定控制量、优化目标和约束条件。

2)弹道优化问题的离散：分别采用打靶法(仅离散控制量)和配点法(同时离散控制量和状态量)将弹道优化问题转化为多目标优化问题。

3)全局多目标最优解集的构造：采用MOEA/D对控制量离散方法得到的多目标优化问题进行优化计算。设置合理的优化参数，如种群规模和迭代步数，获得全局多目标最优解。

4)最优解集的精细优化：采用非线性规划算法对配点法得到的优化问题进行求解，以MOEA/D得到的控制量和状态量作为初始解进行优化迭代，采用自适应配点法进行网格自适应加密以提高求解精度。

需要说明的是：①为了求得全局最优解，首先采用进化算法求解，考虑计算效率问题，采用打靶法仅离散控制量，以降低设计变量的个数；②为了获得较精细的弹道，利用配点法和椭球聚合法将多目标弹道优化问题转化为单目标的非线性规划问题，利用非线性规划算法进行求解，并进行节点自适应加密。

2.2 椭球聚合法

在上述混合求解策略中，利用非线性规划求解多目标问题时，需要用聚合公式将多目标优化问题转化为一组单目标优化问题。为了保持目标函数的连续性，本文采用椭球聚合公式[10]。该方法使用具有特定方向和较大偏心率的椭球(椭圆)与可达目标区域Ω的最优边界相切，并寻找边界上的切点，从而在一定条件下给出PF的近似。

对于极小化问题而言，在大多数情况下，PF是可达目标区域左下边界∂Ω的一部分。椭球聚合公式使用N个椭球(椭圆)与上述边界∂Ω相切。通过位于边界∂Ω上的切点给出PF的近似。该方法要求椭球具有一个较大的长轴和若干个较小的短轴。椭球的中心一般位于可达目标区域的左下侧，通过控制椭球长轴的方向来获得不同的边界点，如图2所示。在一般情况下，当长轴方向均匀分布时，椭球聚合法可以产生近似均匀分布的PF。具体的做法是：将长轴方向与一组均匀分布的权重矢量相关联。

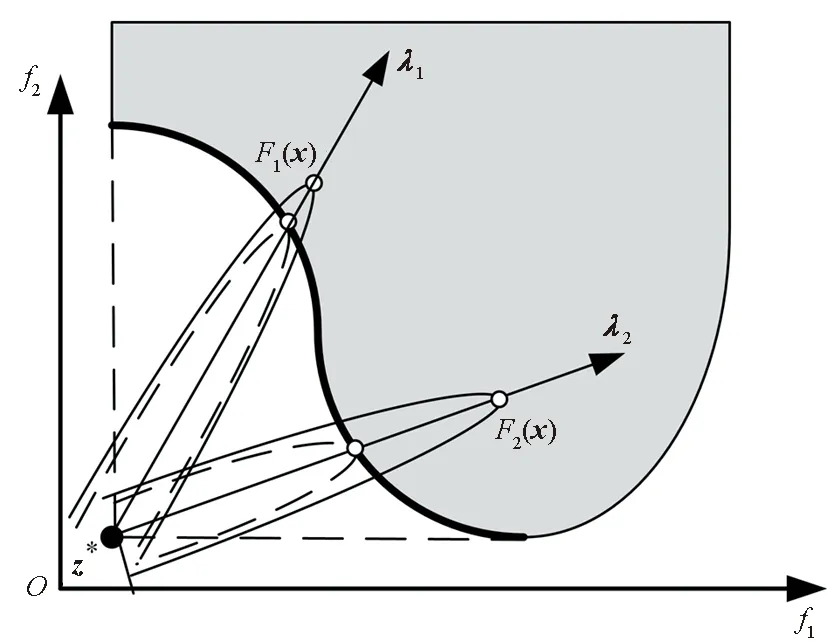
图2 旋转椭球方法Fig.2 Rotated ellipsoid method

根据上述思想，将多目标优化问题处理为N个单目标优化问题。令λ表示权重矢量，R(λ)表示将第一个目标函数F1的坐标轴旋转到权重矢量λ方向的坐标变换矩阵。椭球与边界∂Ω的切点是式(10)所示单目标优化问题的全局最优解。

s.t.x∈Ω

(10)

其中，

(11)

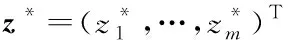
2.3 分解多目标进化算法

分解多目标进化算法MOEA/D由Zhang和Li于2007年提出[13]，该算法将多目标优化问题转化为多个单目标优化子问题，对子问题采用进化算法以合作的方式同时进行优化。因此，其具有进化机制简单、收敛速度快、PF近似均匀等优点。

以椭球聚合公式为例，将原始多目标优化问题分解成N个标量优化问题。令λ1, …,λN为均匀分布的一组权重矢量，z*为参考点，则第j个子问题的目标函数为

(12)

因为gRE关于λ连续，所以当权重矢量λi和λj相互接近时，子问题gRE(x|a,R(λi),z*)的优化解应该接近gRE(x|a,R(λj),z*)的优化解。因此与权重矢量λi相邻的关于gRE的信息能够对子问题gRE(x|a,R(λi),z*)的优化起到辅助作用。MOEA/D包括初始化、更新和停止三个过程，具体步骤见文献[13]。

在MOEA/D中，通常采用欧式距离测量两个权重矢量之间的邻近性，并用于确定矢量λi的邻居。获得较为精确的参考点z*通常需要求解多个单目标优化问题，比较耗时，因此该算法首先进行初始化，然后在迭代过程中进行更新。这样可以使得理想点的更新随着迭代优化而进行，节省了计算时间。

2.4 自适应配点法

针对轨迹优化问题中精度和效率之间的矛盾，丰志伟等曾提出基于二代小波的节点自适应加密方法[9]。该方法采用Runge-Kutta方法将原轨迹优化问题转化为非线性规划问题，并采用非线性规划算法求解；根据控制或状态函数的小波系数幅值确定自适应加密的节点，并进行序列优化。

基于二代小波的节点自适应算法输入参数包括：初始分辨率水平J0(控制初始节点个数)；最大分辨率水平Jmax(控制背景节点个数，即最小节点间隔)；小波系数幅值的阈值ε。终止条件：前后两次节点位置相同或达到预定的迭代次数。计算流程如下：

1)根据初始分辨率J0生成均匀节点GJ0(或{τi})以及该均匀节点上的状态函数x和控制函数u的初始猜测；

2)利用非线性规划算法优化由原轨迹优化问题转化得到的非线性规划问题，得到状态函数x和最优控制函数u；

3)根据节点自适应算法确定下一步优化的自适应节点，若存在多个控制函数，则将这些控制函数分别得到的自适应节点进行合并；

4)利用前一次优化计算的解x和u，利用小波插值计算新的自适应节点上的初始猜测，并进行循环迭代，直到满足终止条件。

需要说明的是，小波系数幅值的阈值通常可取为ε=γ(umax-umin)。对于间断函数，γ可取0.005～0.01；对于连续函数，γ可取0.001～0.005。

3 仿真分析

3.1 仿真条件和参数

以通用航空飞行器[14](Common Aero Vehicle，CAV)气动性能为例进行多目标弹道优化，通过拟合可得到CAV-H模型的气动系数

(13)

优化指标包括射程最大和总加热量最小。考虑的约束条件包括驻点热流密度、动压、过载以及禁飞区约束，仿真参数设置如表1所示。

利用本文提出的混合优化算法，将攻角和侧倾角离散为15个点，加上终端时间共31个设计变量。

在MOEA/D优化过程中采用旋转椭球聚合公式，种群规模(子问题个数)为300，迭代步数为1000，邻居规模为20。采用300个均匀分布的权重矢量，每个权重矢量的分量为正值，和为1。节点自适应算法中，为了节省时间，将优化子问题数目取为21，小波系数幅值的阈值取εi=0.001·(uimax-uimin)。针对每个子问题，取MOEA/D优化结果中相应权重系数对应的子问题的解(控制量和飞行时间)进行积分得到状态变量，并作为配点法中的初始解。采用序列二次规划算法SNOPT[15]求解非线性规划问题。

表1 弹道优化约束条件

3.2 弹道约束条件处理

由于MOEA/D无法直接处理多目标弹道优化问题中存在的复杂非线性约束，需要对约束进行处理。对于不等式约束，在聚合目标gte(x|λ)中引入惩罚项，MOEA/D算法更新新解时不仅考虑了解的聚合目标，而且还融合了约束违约程度。采用罚函数的MOEA/D在求解控制-结构一体化设计中得到了成功应用[16]。

假设第i个约束gi(x)≤0,i=1,…,nc的违约度[17]定义为

Wi(x)=max[0,gi(x)],i=1,…,nc

(14)

如果Wi(x)=0，则x可行，否则不可行。将目标函数修改为

F′(x)=[f1(x)+aW,…，fm(x)+aW]T

=[f′1(x),…，f′m(x)]T

(15)

其中

W=max[W1,…,Wnc]

(16)

nc是约束的个数，参数a>0。

3.3 优化结果分析

利用进化算法得到的近似PF如图3所示，从图中可以看出，最大射程解在图中以“▽”标示，此时射程为13 799 km，总加热量为18 173 MJ/m2；最小总加热量解以“△”标示，此时总加热量为10 745 MJ/m2，射程为10 930 km。两个目标具有明显的冲突性，即射程最大时，总加热量也最大，反之亦然。为了进一步对比分析，图4给出了三条多目标优化典型弹道(两条单目标最优弹道；一条典型折中解，图3中以“□”标示)对应的控制量以及主要弹道参数。从图4曲线可以看出，最大射程弹道的攻角为最大升阻比攻角；最小总加热量弹道攻角较大，且高度在纵平面大幅跳跃。

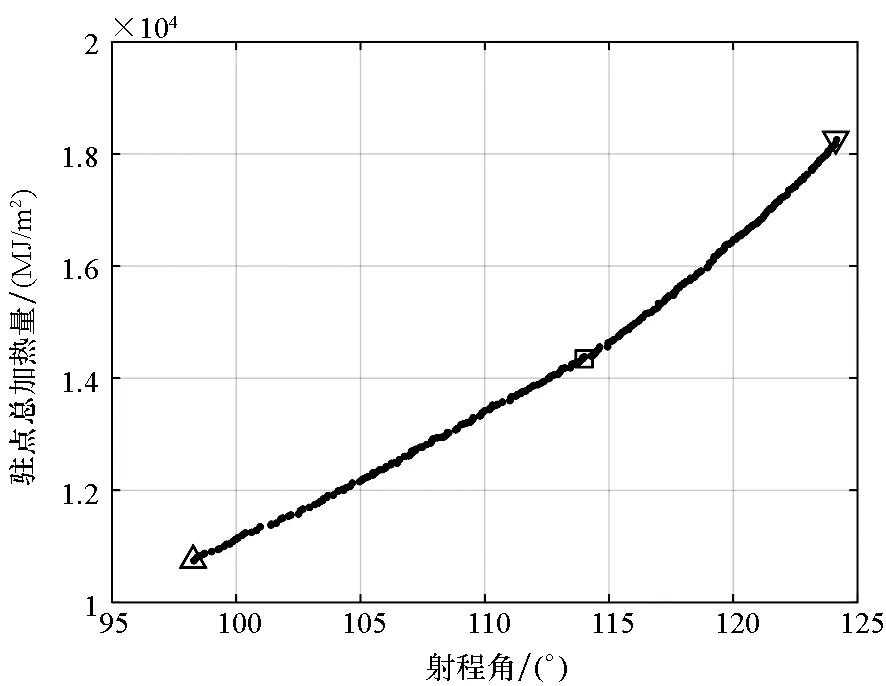
图3 最大射程-最小总加热量两目标PFFig.3 PF for maximizing down range and minimizing total heating

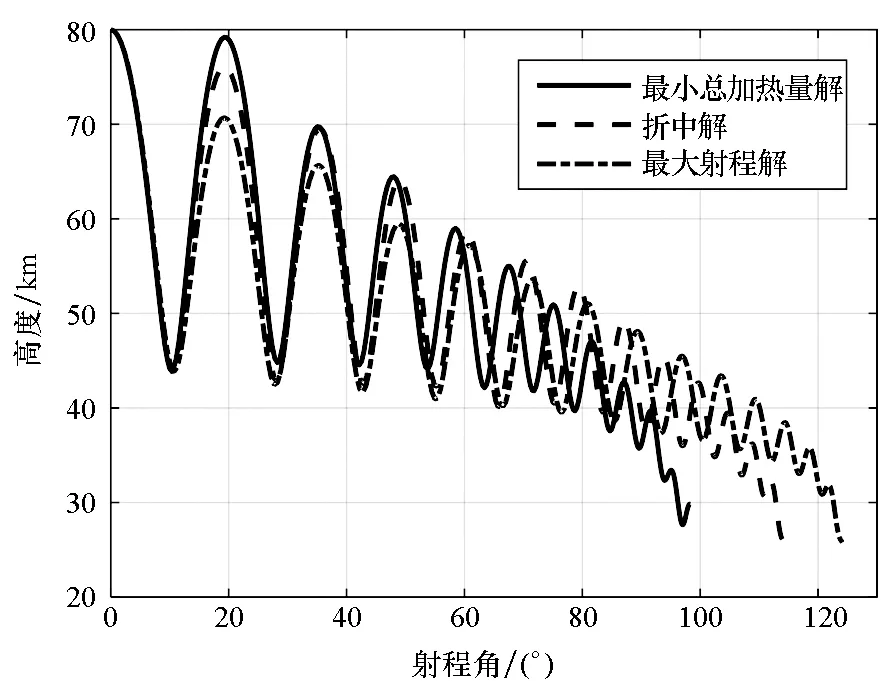
(a) 高度(a) Height

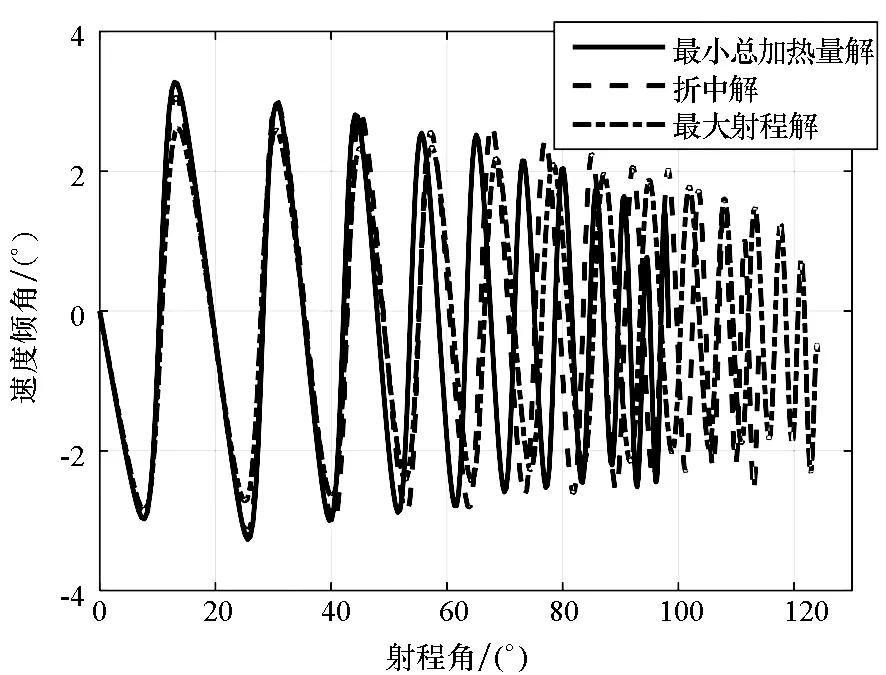
(b) 速度倾角(b) Velocity dip angle

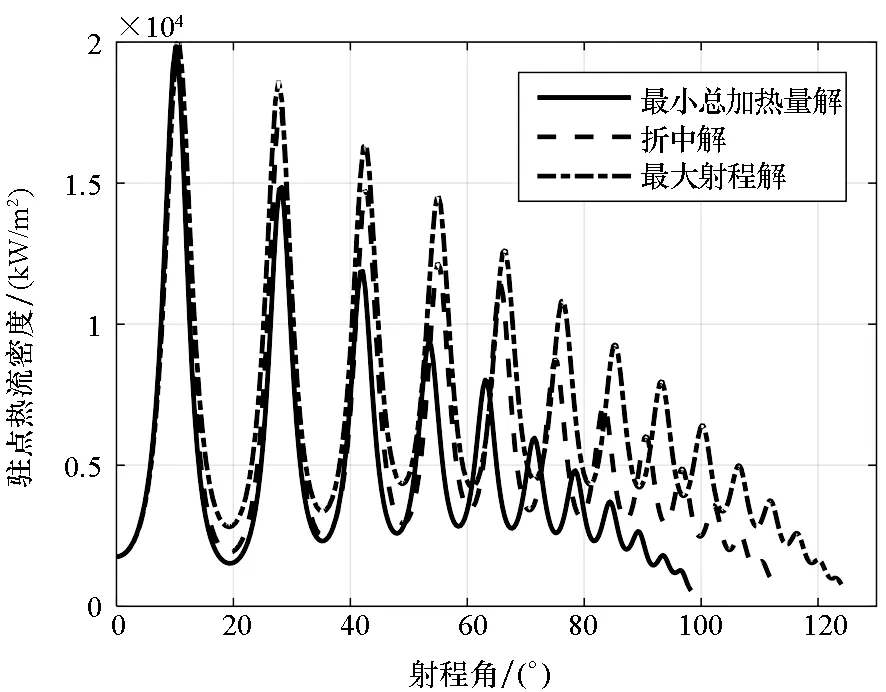
(c) 驻点热流密度(c) Heating rate of stagnation point

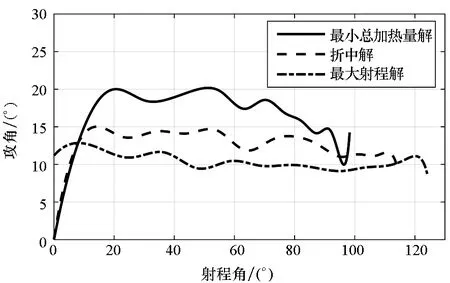
(d) 攻角(d) Attack angle

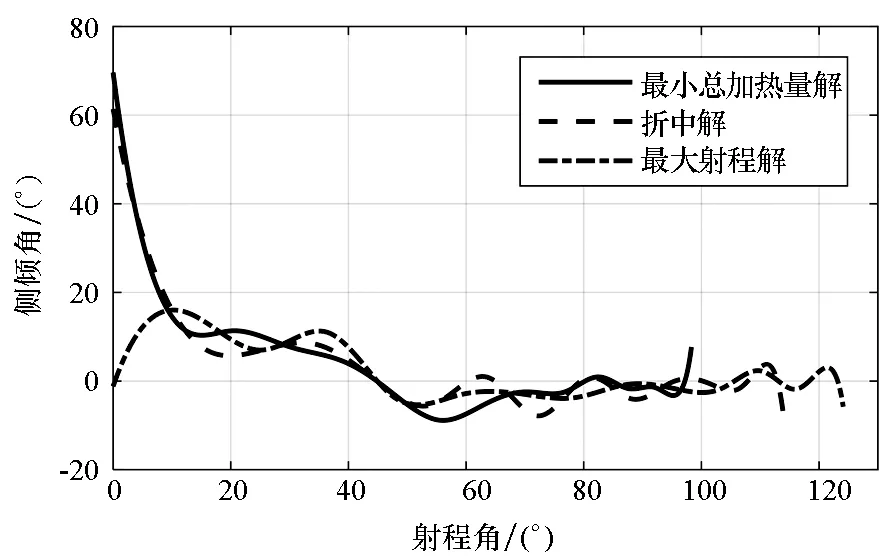
(e) 侧倾角(e) Bank angle图4 多目标优化弹道典型解(MOEA/D)Fig.4 Typical solutions of multiobjective trajectory optimization (MOEA/D)

采用自适应配点法优化得到的近似PF如图5所示，与进化算法MOEA/D优化得到的近似PF相比，近似PF得到较好的改善。在最大射程解附近，MOEA/D较接近配点法获得的解，而在最小总加热量解附近其偏差较大。由此说明采用15个点近似攻角和侧倾角来优化最大射程是足够的，但是为了优化最小总加热量弹道，需要增加设计变量的个数。

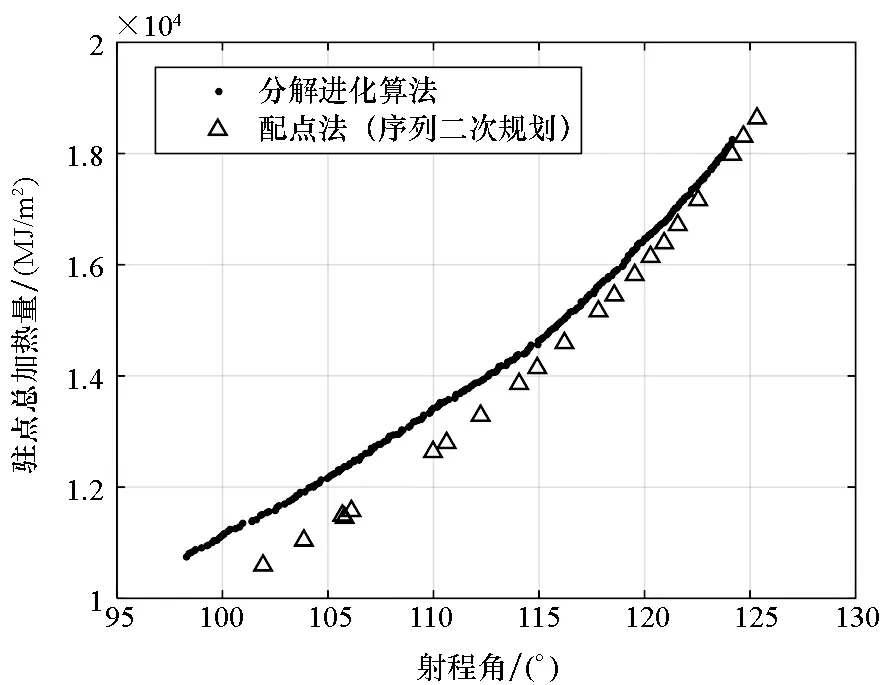
图5 两种方法的PF对比Fig.5 PF comparison of two methods

自适应配点法优化得到的攻角和侧倾角曲线如图6所示。整体规律与进化算法得到的解一致，但是最小总加热量解攻角曲线更复杂。

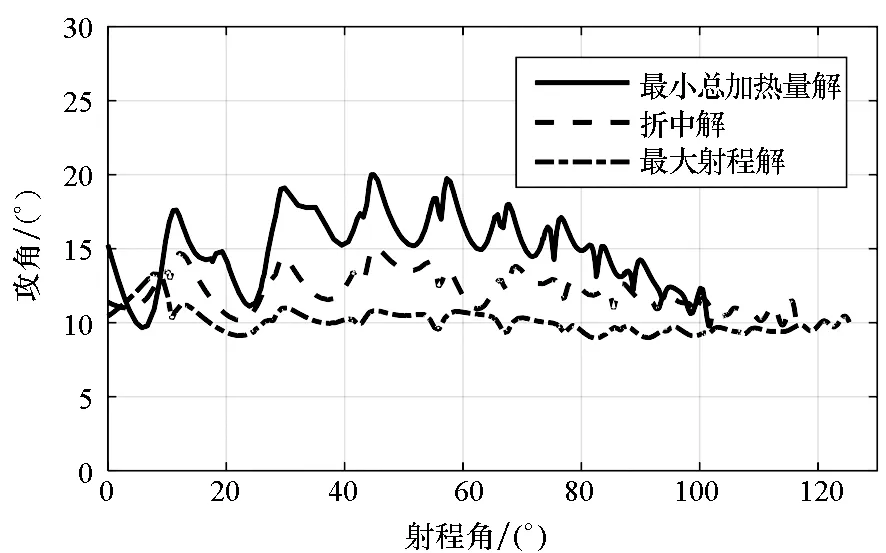
(a) 攻角(a) Attack angle

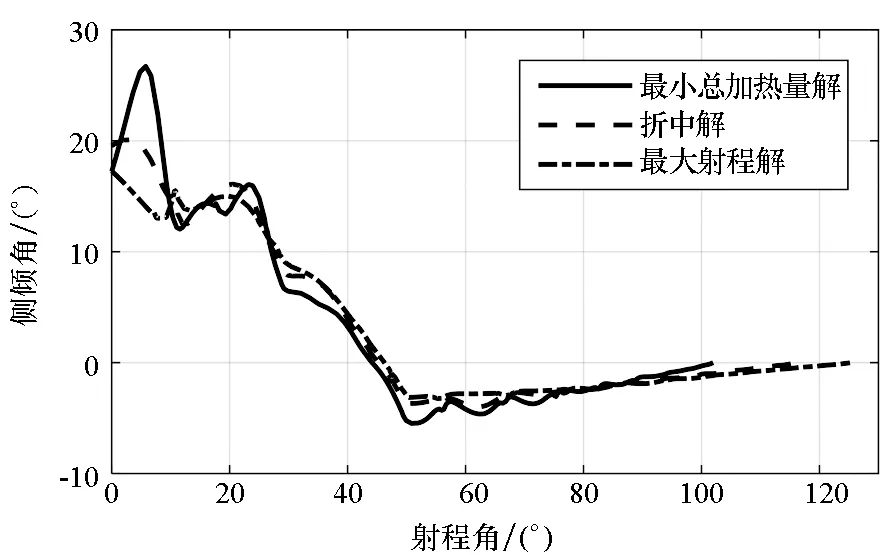
(b) 侧倾角(b) Bank angle图6 多目标优化弹道典型解(自适应配点法)Fig.6 Typical solutions of multiobjective trajectory optimization (adaptive collocation method)

4 结论

针对滑翔飞行器多目标弹道优化设计问题，综合考虑计算效率和精度，结合分解多目标进化算法和自适应配点法提出一种分层、混合优化方法。以美国CAV-H为例进行仿真分析，计算结果验证了所提混合优化方法的有效性，不论是MOEA/D还是配点法，均能够得到较均匀分布的Pareto前沿。