顾及诱发因素响应的灰色极限学习机滑坡位移预测
高彩云,高 宁,杨福芹,苗林光,苑春雨
(1.河南城建学院 测绘与城市空间信息学院,河南 平顶山 467036;2.河南工程学院 土木工程学院,河南 郑州 451191)
滑坡是一种常见的地质灾害,它的发生不仅给人类的生命、财产安全带来严重威胁,同时给资源、生态、环境等带来巨大破坏[1]。滑坡位移的准确预测对于指导灾害预防具有重要作用。目前,综合利用滑坡各类监测数据,建模分析滑坡位移趋势,已成为滑坡位移预测领域的实际方向。为此,时序分析、指数平滑、GM(1,1)模型、BP(back propagation)算法、SVR(support vector regression)等被广泛应用于各种类型的滑坡位移预测中[2-4]。由于各类滑坡体组成物质和演化过程各异,并实时受到降雨、库水位、荷载等诱发因素的综合作用,同时由历史数据衍生的预测模型无法体现预测过程的时效性和准确性,因此在提升预测模型数学精度的同时,如何将诱发因素的影响纳入滑坡位移预测模型中逐渐成为研究的新趋势[5-7]。
论文以三峡库区两滑坡体为例,首先基于其变形演化特征与诱发因素分析,将滑坡累积位移分解为趋势项和随机项,然后利用动态GM(1,1)模型对趋势项进行拟合和预测,基于诱发因素的响应构建ELM模型预测随机位移项,最后将趋势项和随机项位移预测值叠加,实现滑坡位移预测。
1 动态GM(1,1)-ELM滑坡位移预测模型
1.1 顾及诱发因素响应的耦合建模思想
滑坡位移的产生受内在因素(坡体自身地质条件)及诱发因素(降雨、地下水、人类工程活动等)耦合作用影响[1,8-9],其位移变化量可以依据各影响因素作用形式的不同分解为不同的响应成分,通常可用公式(1)响应成分模型表示[5]:
Yt=Ut+Vt
(1)
式中:Yt为滑坡变形位移,Ut为趋势项,Vt为具有不确定性的随机波动项。趋势项是指滑坡位移序列变动的总体方向,受控于内在因素;随机项主要受诱发因素控制。顾及诱发因素响应的灰色极限学习机滑坡位移预测模型,其思想是借助灰色GM(1,1)模型提取滑坡位移的趋势特征,采用ELM算法,并考虑降雨、地下水等诱发因素基础上,实现对随机波动项的逼近提取,耦合建模流程如图1所示。
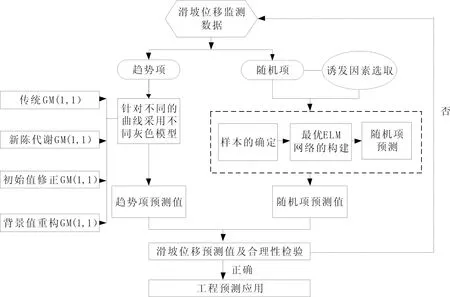
图1 顾及诱发因素响应的GM(1,1)-ELM滑坡位移预测模型
1.2 滑坡位移趋势项的GM(1,1)提取
滑坡体的蠕变过程通常包括三个阶段:初始变形阶段、匀速变形阶段、加速变形阶段(如图2所示),滑坡体在不同的变形阶段,其滑坡变形位移曲线形式不同,故可采用不同形式的GM(1,1)模型对趋势项进行提取。
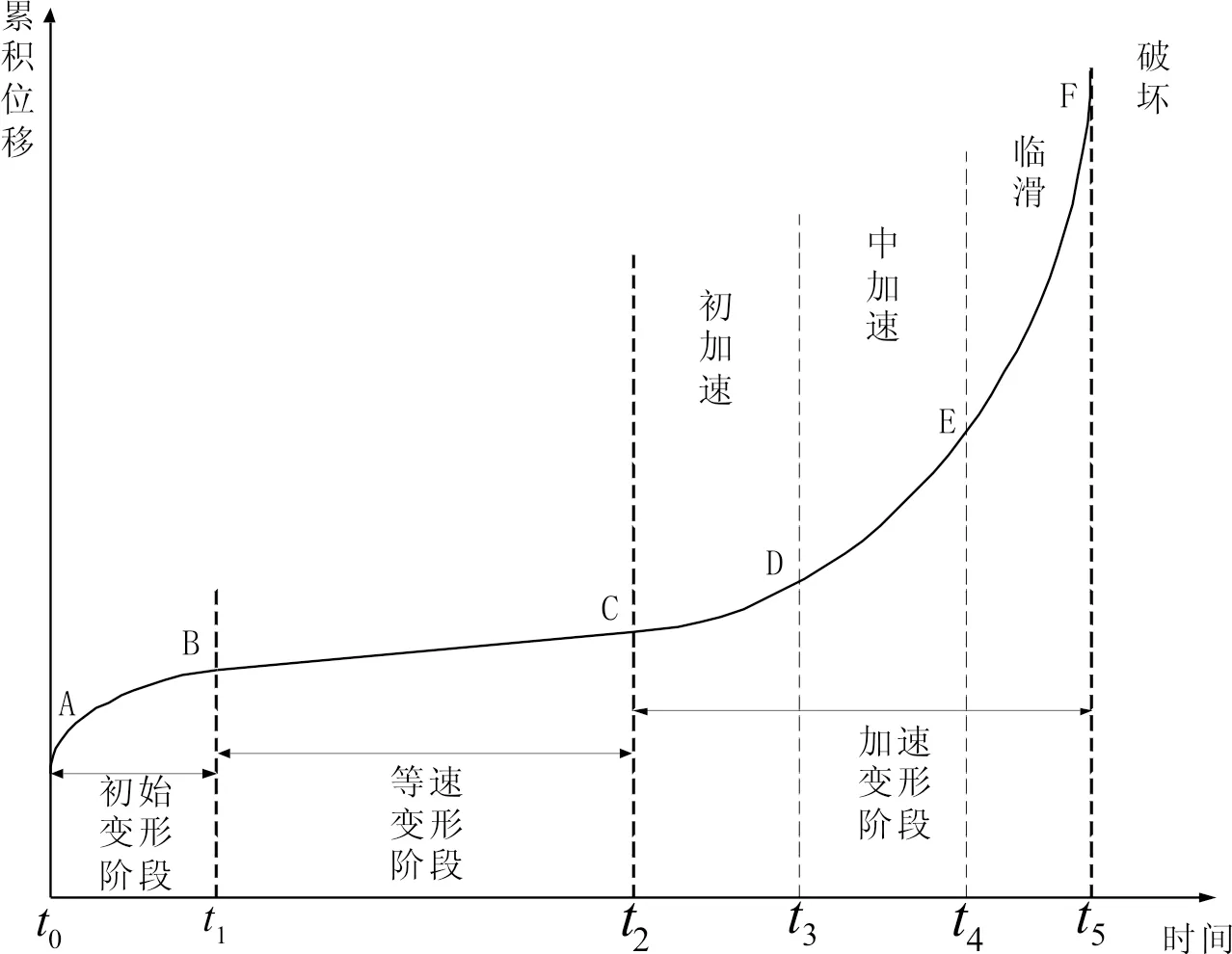
图2 滑坡蠕变阶段曲线
传统GM(1,1)模型(建模过程见文献[10]所述)适用于滑坡变形位移序列为齐次指数序列或近似齐次指数序列的建模预测。新陈代谢GM(1,1)模型体现出新信息优先原理,建模时在原滑坡位移序列中置入最新位移信息,同时删除最老的历史数据,用新序列不断滚动建立GM(1,1)模型,该方法克服了传统 GM(1,1)建模时过度依赖滑坡历史数据的缺点,能显著提高中长期预测的精度。
初始值修正GM(1,1)模型是指在传统GM(1,1)基础上,基于新信息优先原理,取x(1)(n)选为初始条件,即预测公式为:
(2)
或基于最小二乘约束下对初始条件选取。
背景值修正GM(1,1)模型是将传统GM(1,1)模型背景值z(k)固定权改为变权构造背景值的方法,或将数据序列抽象为指数函数或非齐次指数函数构造背景值,经背景值修正后的GM(1,1)模型,适用于滑坡位移数据变化剧烈的情况。
1.3 滑坡位移随机项的ELM逼近
滑坡位移的随机波动项受降雨、库水位变化、地下水、人类活动等影响,是一个复杂的非线性序列,论文采用ELM对其进行逼近提取。
ELM是一种新型单隐层前馈神经网络[9,11,12],该网络克服了传统梯度下降算法(如BP、RBF算法)学习速度缓慢、易限于局部极小、网络泛化能力差的局限性。根据滑坡变形诱发因素集和位移变形序列,选取训练样本{xi,ti},xi∈Rp,ti∈Rq,i=1,2,…Ν,则激励函数为g(x),隐含节点数量为L的ELM数学模型为[12-13]:
(3)
式中,yj为期望输出,βi表示隐含层第i个神经元与输出层神经元间的连接权值,wi为输入层和隐含层间的连接权重,bi为隐含层节点阈值,激励函数g(x)为Sigmiod函数,数学表达为:
g(x)=1/(1+e-x)
(4)
假定L=N,则对于任意给定的wi,bi,ELM都可以零误差逼近训练样本,即:
(5)
考虑式(3),则式(5)表达为:
(6)
其矩阵形式为:
H·β=T
(7)
其中,
当g(x)无限可微时,ELM以网络训练误差最小,并使输出权值系数范数最小为约束条件,即:
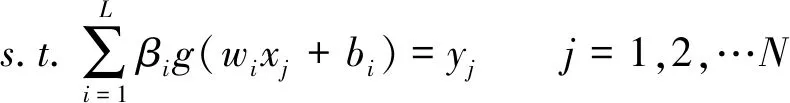
(8)
2 工程实例应用
实例1:新滩滑坡位于湖北省秭归县长江西陵峡上段兵书宝剑峡口北岸,距长江三峡大坝约26 km。新滩滑坡为堆积体滑坡,堆积物厚度约为30~40 m,滑坡长约2 km,中部宽0.4 km,于1985年6月曾发生大规模的滑动,约有几百万立方米的岩土体滑入长江[14],滑坡体规模达300万m3,其中B3监测点,从1978年至1985年,共计89期监测数据,其位移变形曲线如图3所示。
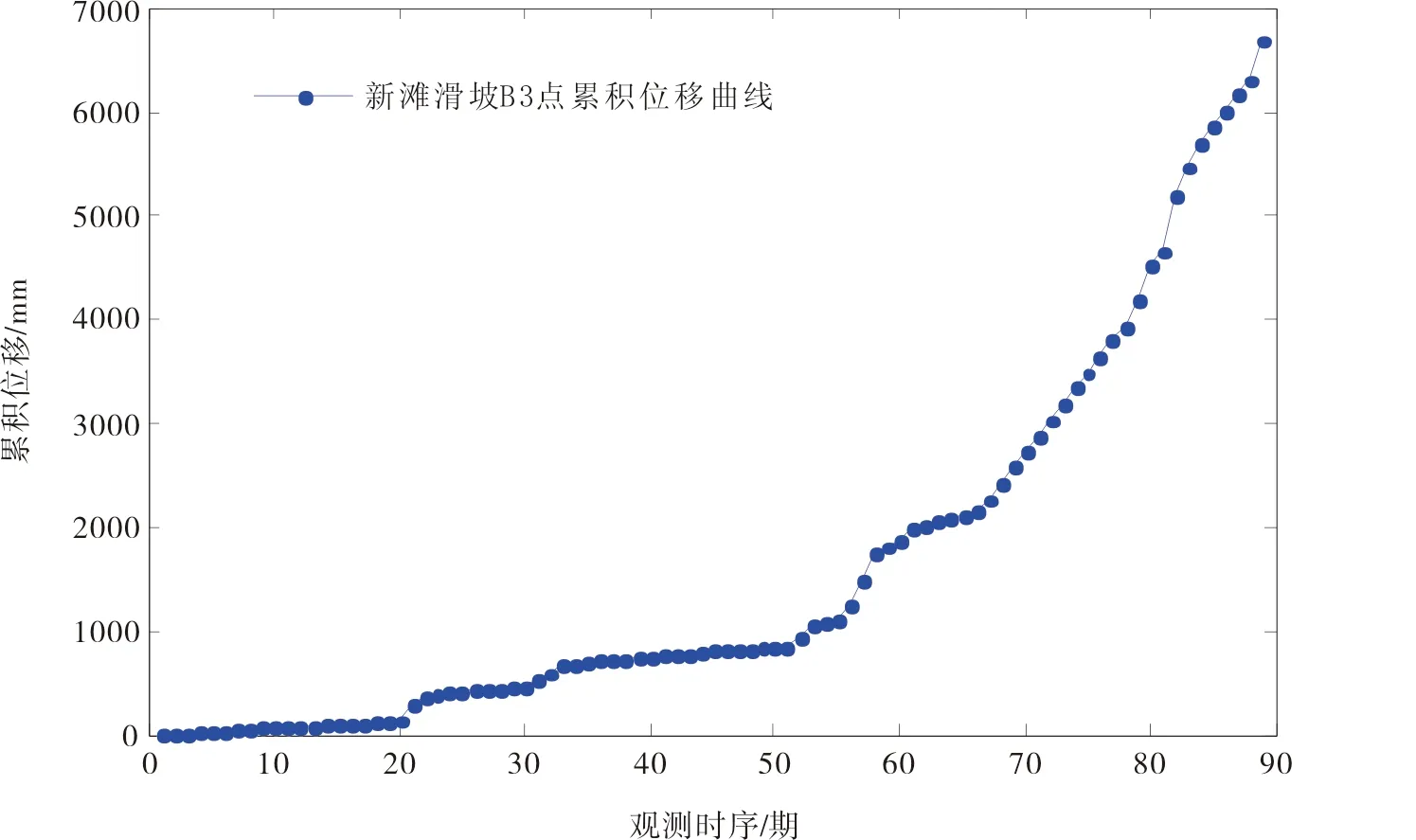
图3 新滩滑坡B3点监测位移曲线
实例2:三峡库区某滑坡GPS2-2监测点[5]。
该滑坡体位于三峡库区内,滑体主要为第四系全新统滑坡堆积层,岩性主要为粉质黏土,滑坡前缘临江且已涉水,后缘高程为290 m,监测数据共计29期。
2.1 新滩滑坡B3点位移预测
(1)新滩滑坡B3点诱发因素分析
由图3可知:新滩滑坡变形并不是单调变化,而是有急、有缓起伏的变化,共经历了初始蠕变期、匀速蠕变期、加速蠕变期、剧变破坏期四个阶段,其位移曲线表现出明显台阶状特征,由于新滩滑坡位于多雨区,每年5~9月为多雨季,年降雨量约为1 016 mm,绘制月降雨量与月位移量关系图(见图4),发现在雨季时,滑坡位移量多在增大,非雨季时则较平稳甚至停滞,考虑式(1),故将降雨量作为B3点随机项的主要诱发因素[9,14]。
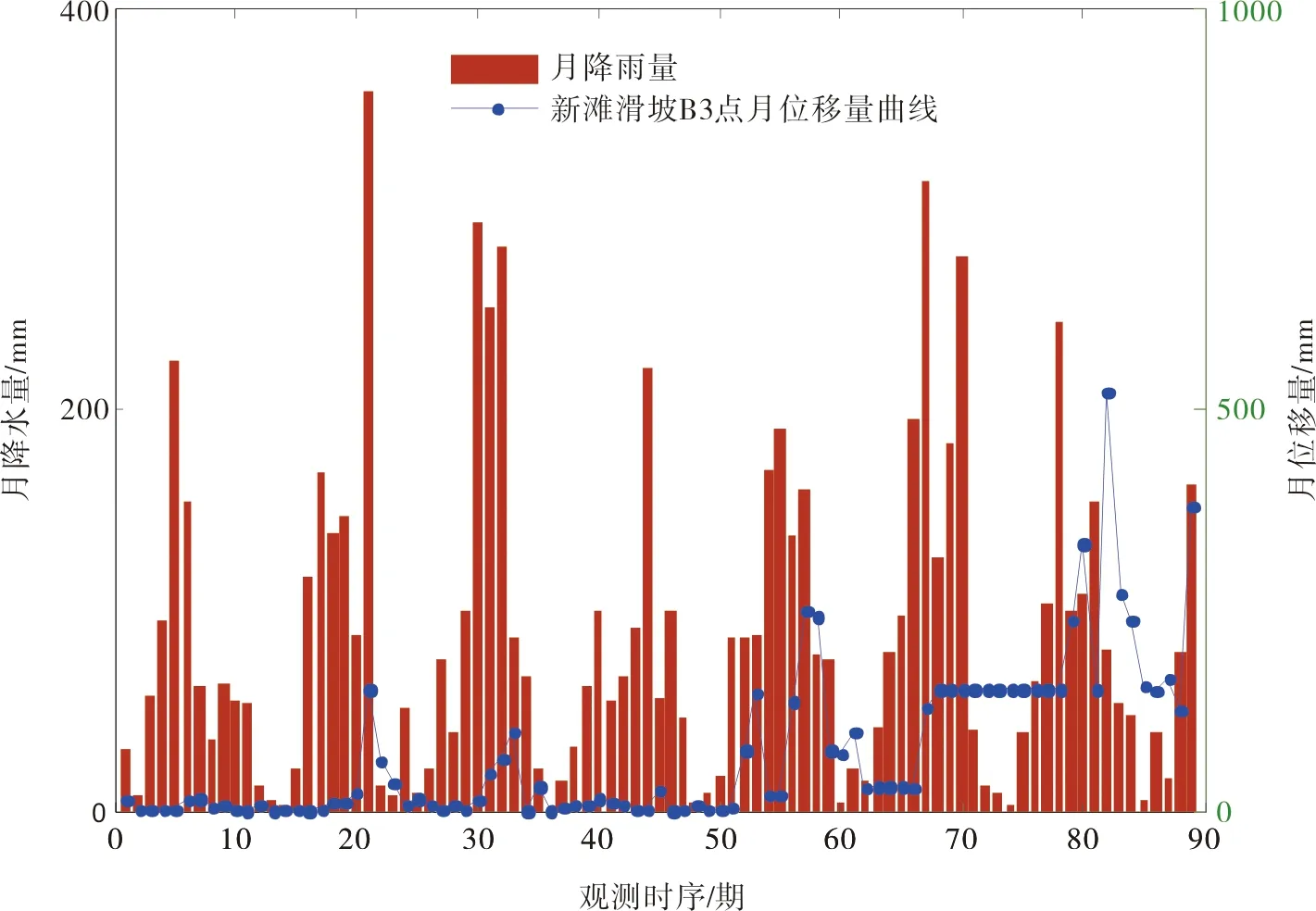
图4 新滩滑坡B3监测点月降雨量与月累计位移的关系图
(2) 顾及降雨的GM(1,1)-ELM新滩B3点变形预测
① B3监测点位移趋势项的GM(1,1)提取
考虑B3监测点位移变化的台阶状特征,采用“等维新信息滚动”GM(1,1)模型提取位移趋势项,优选后建模序列长度为20维,利用1~80期数据建模,对81~89期进行趋势预测,趋势项提取见图5。
② B3监测点位移随机项的ELM逼近
将月降雨量作为ELM网络的输入,输出项为随机项预测值(GM(1,1)预测后的残差项),隐含层神经元激励函数为Sigmoid函数,隐含层最优神经元数为3,逼近效果见图6。
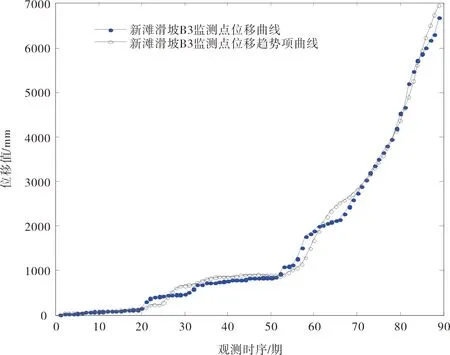
图5 新滩B3监测点位移趋势项曲线
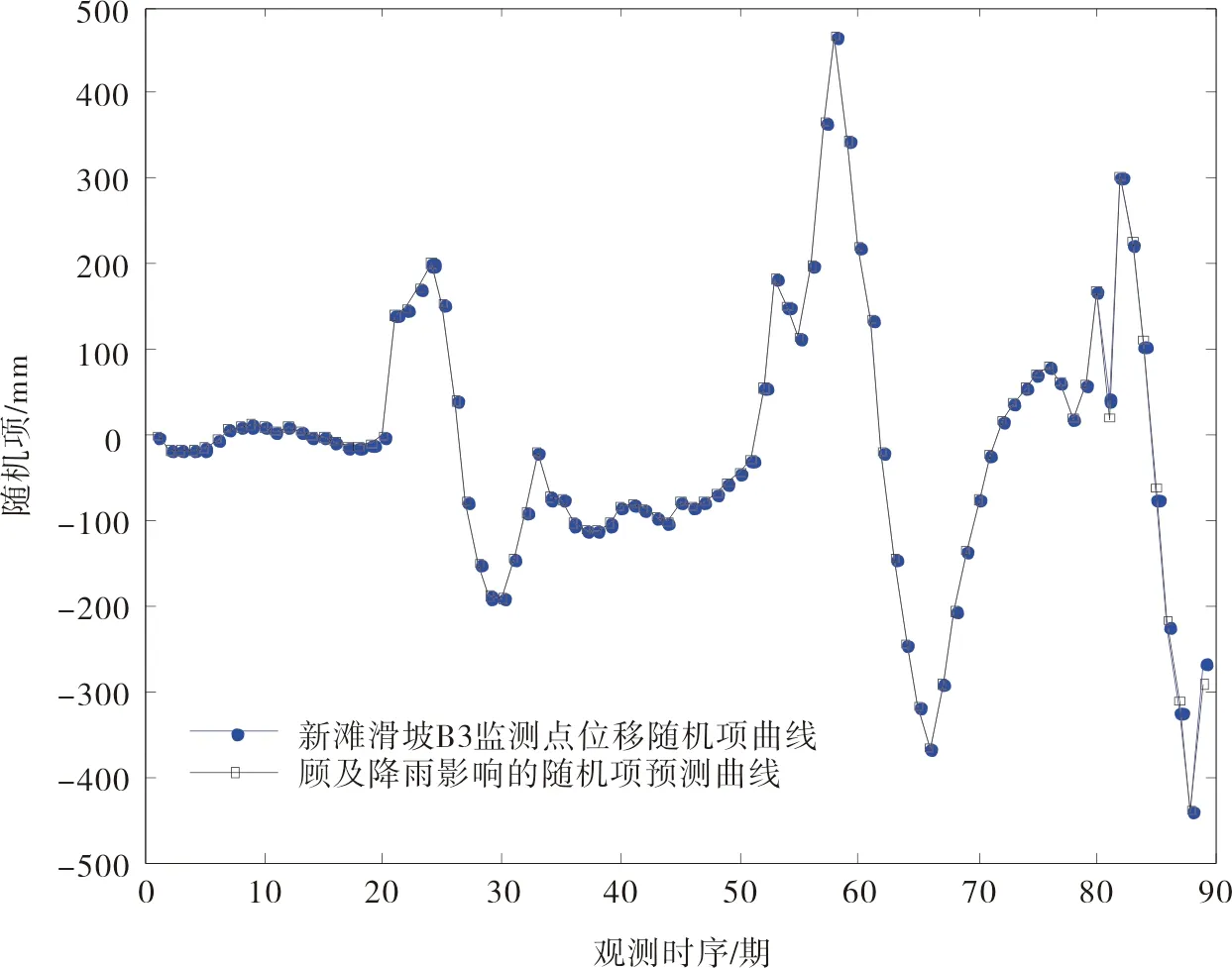
图6 新滩B3监测点位移随机项曲线
③耦合预测
新滩滑坡B3点81~89期耦合预测结果如表1所示。为便于比较,同时构建了未考虑诱发影响因素的GM-ELM预测模型,结果列于表1。
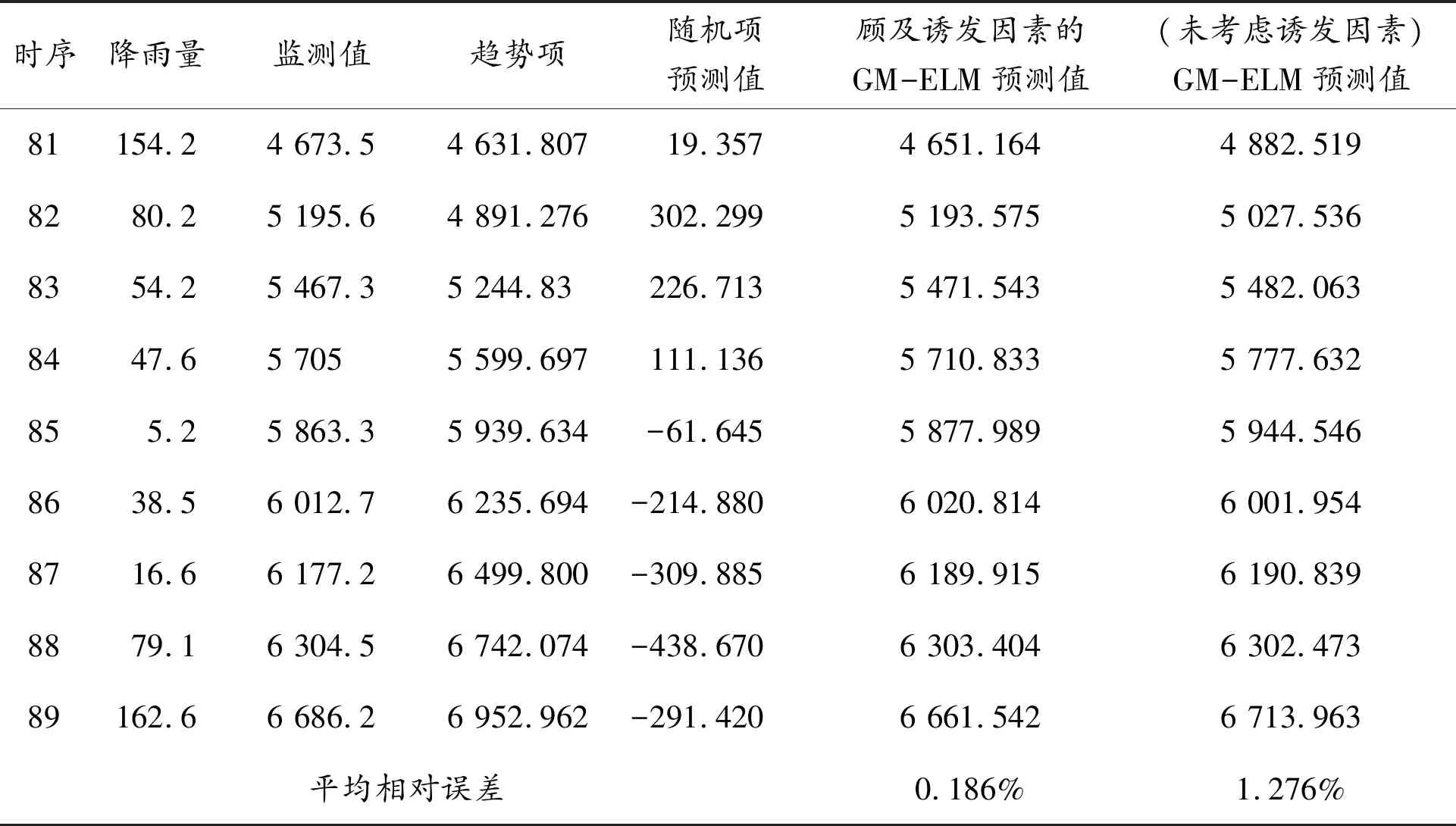
表1 顾及降雨影响的GM-ELM模型预测结果(新滩滑坡B3点) mm
2.2 三峡库区某滑坡GPS2-2监测点位移预测
(1)GPS2-2诱发因素分析
该滑坡岩土体流变行为除受自身性质、滑体重力和边界条件控制外,同时受到外界诱发因素的强烈影响,已有研究成果表明,降雨、库水位变化是主要诱发因素。GPS2-2监测点位移量、降雨及库水位关系见图7。
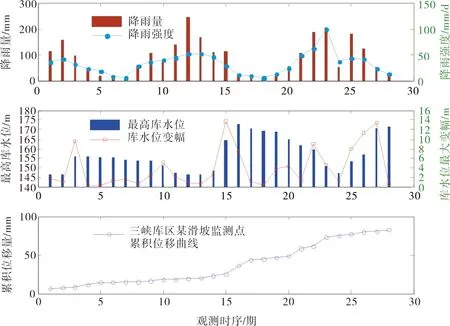
图7 三峡库区某滑坡GPS2-2监测点累计位移与降雨量、库水位关系图
(2) 顾及降雨、库水位信息的GM-ELM GPS2-2点变形预测
① GPS2-2监测点位移趋势项的GM(1,1)提取
采用“等维新信息滚动”GM(1,1)模型提取位移趋势项,优选后建模序列长度为4,利用1~28期数据建模,对29~30期进行趋势预测,趋势项提取见图8。
② GPS2-2监测点位移随机项的ELM逼近
将降雨量、降雨强度、最高库水位、库水位变幅、最大降速、最大升速六种诱发因素信息作为ELM网络的输入,输出项为随机项预测值(GM(1,1)预测后的残差项),隐含层神经元激励函数为Sigmoid函数,隐含层最优神经元数为3,逼近效果见图9。
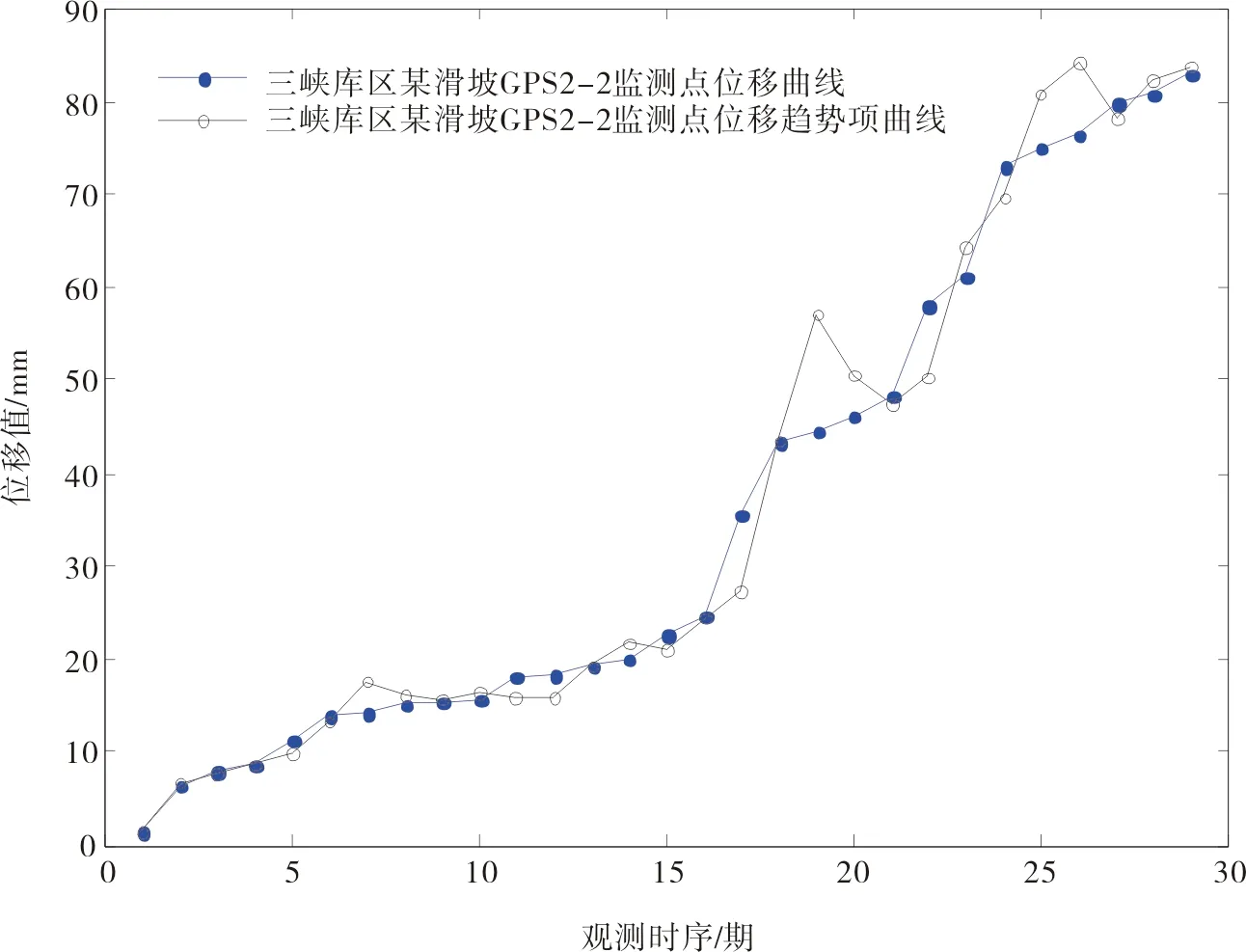
图8 三峡库区某滑坡GPS2-2监测点位移随机项曲线
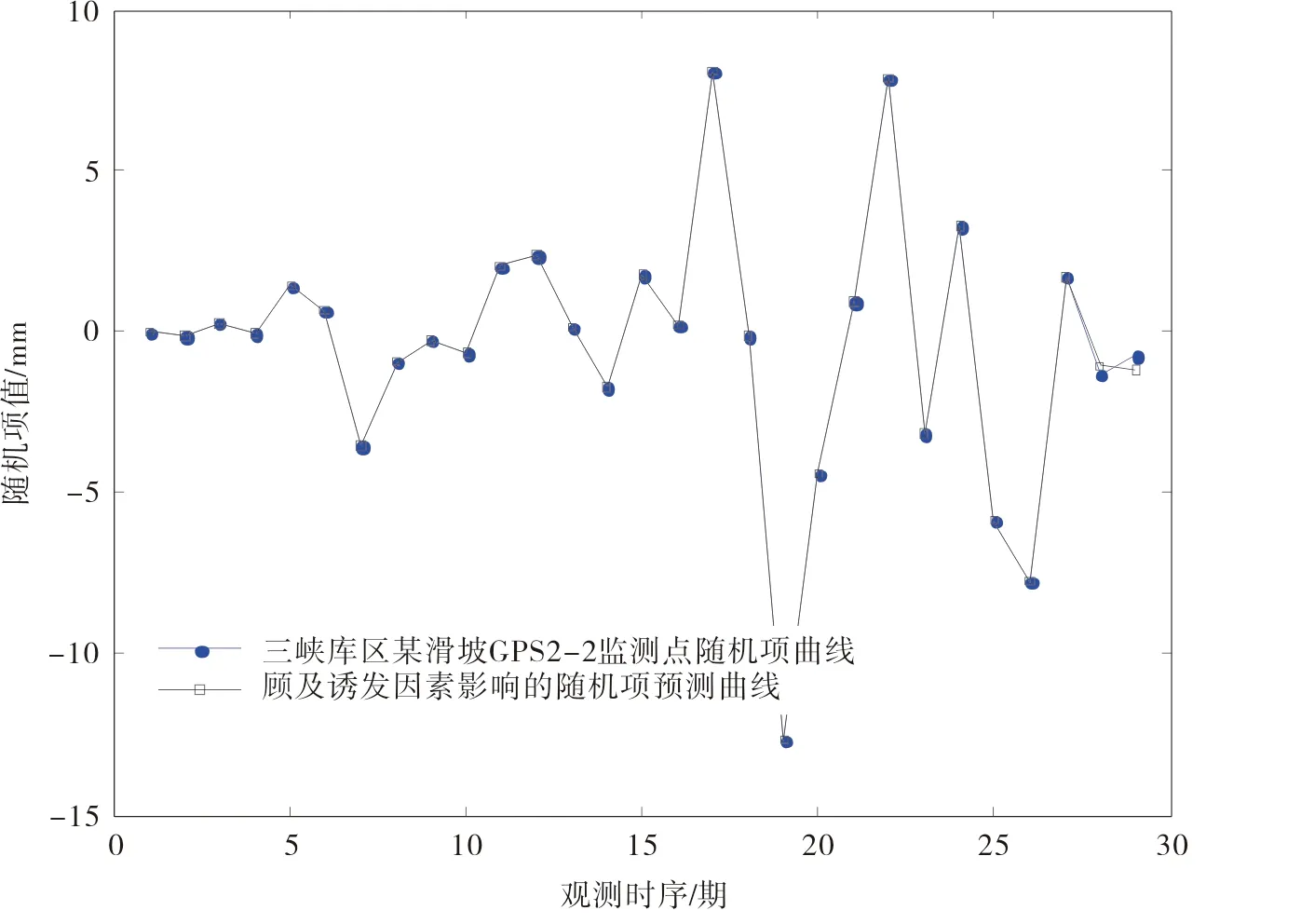
图9 三峡库区某滑坡GPS2-2监测点位移随机项曲线
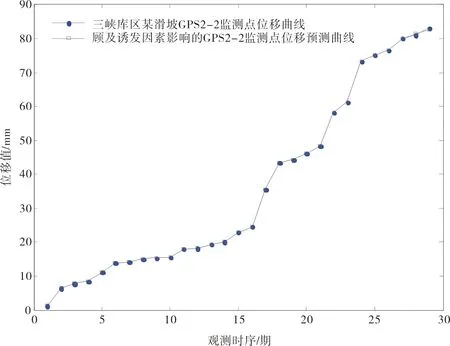
图10 顾及降雨、库水位影响的GM-ELM模型
③ 耦合预测
三峡库区某滑坡GPS2-2监测点1~29期整体预测效果如图10所示,28~29期耦合预测结果见表2。

表2 顾及降雨、库水位影响的GM-ELM模型预测结果(GPS2-2点) mm
3 结论
(1)滑坡的内因主要决定了滑坡变形发展的总体趋势,而诱发因素如季节性降雨、库水位变化等则加速了滑坡的变形破坏;
(2)顾及诱发因素响应的GM-ELM模型,能结合滑坡监测数据的特点,从数据分解角度出发兼顾了数据的趋势性与随机性,同时考虑了滑坡体的诱发因素影响,从多角度充分利用了滑坡监测数据的有效信息且预测精度较高。

