一种防空导弹制导精度影响因素的定量分析方法*

付 昊，李克勇，郑国栋，漆 斌，居 闽

(1.海军装备部驻上海地区第六军事代表室·上海·201109； 2.上海机电工程研究所·上海·201109)

0 引 言

在进行防空导弹方案设计时，需要对系统指标进行逐级分解。指标分解的合理性不仅决定了各分系统及组件的具体技术途径，也对总体指标的实现产生着影响。主动雷达寻的制导是先进防空导弹的主要制导方式之一，作为导弹技术指标实现的核心部件，合理的技术指标要求十分重要。主动雷达导引头的作用距离、测角精度、时间常数等决定了末制导精度，但具体的影响情况却较难量化，这导致了制导控制系统指标分解的合理性无法被评估。

导弹制导精度的评估方法主要有蒙特卡洛打靶法[1]和伴随方法[2-6]。蒙特卡洛方法可针对不同的误差源和飞行弹道进行对脱靶量的正向评估。但是，弹道仿真数量大，耗时长，不利于对影响因素进行定量分析。同时，导引头模型和指标的数学描述对仿真结果影响很大。基于比例导引而发展的伴随方法可以用于制导精度影响因素的定量分析。伴随方法依据的是线性化模型，尽管文献[2]中的对比分析认为线性化模型与非线性模型差别不大，但是对于防空导弹而言，其对制导精度的要求是达到亚米级，模型误差会对结果评估带来较大的相对误差。针对雷达制导，测角误差、目标角闪烁、初始指向误差等对制导精度的影响分析被广泛研究[7-9]。由于采用伴随方法，无法对导引头探测盲距、导弹最大可用过载等由非线性因素导致的脱靶量进行分析。此外，导弹自动驾驶仪响应特性[10]、导引头解耦特性[11]等也会对制导精度产生影响。

针对主动雷达制导防空导弹末制导精度定量分析的现实需求，以及现有方法存在的不足，本文提出了一种基于物理模型的制导精度快速评估方法，从建立由主动雷达导引头指标描述的数学表征出发，采用数值评估手段，获得了比例导引末制导精度影响因素的定量分析准则，并将通过算例的数值分析，给出具体分析结果，用于指导导弹制导控制系统指标的合理分解。

1 制导精度影响因素分析

主动雷达制导导弹采用比例导引方法，影响闭环制导精度的因素主要包括导引时间、初始指向误差、目标机动、比例导引系数、导弹可用过载、视线角测量误差、视线角速度误差及延迟、目标探测盲距、弹目交汇姿态和速度等。这些影响因素大致可以分为两类，一类是条件因素，由弹目的运动属性决定，其约束了导引过程的条件场景；另一类是指标因素，由导引头性能和弹体性能决定，需要通过制导控制系统指标分解进行合理设计。

在比例导引过程中，导引头探测距离制约着导引时间。在一定初始指向误差前提下，导引时间越短，对弹体响应速度和过载能力的要求越高。弹体特性达不到理论要求，将会导致脱靶量增加。当弹目距离小于探测盲距时，导引头不再准确输出视线角和实现角速度信息，预测的遭遇点不再更新。假设导引头探测盲距为100m，视线角误差为1°，则对应预测的遭遇点偏差约为2m。视线角误差除了会直接引起一定脱靶量外，还将导致持续的附加过载要求。视线角抖动导致视线角速度误差及延时较大，在一定导弹过载能力下，这使得视线角速度发散时间提前，脱靶量增大。

2 数学描述

2.1 比例导引

理论上，比例导引过程与导弹和目标的姿态无关，导引头解耦(耦合弹体姿态运动)的能力对比例导引的影响可通过导引头测角误差来表征。因此，比例导引的输入参数包括：

(1)导弹位置坐标x、y、z，速度大小V，速度倾角θ，速度偏角ψc；

(2)目标位置坐标xT、yT、zT，目标速度大小VT，目标速度倾角θT，目标速度偏角ψT；

(3)导弹可用过载nmax；

(4)比例导引系数N

比例导引规律

(1)

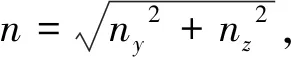
如果n>nmax, 那么

(2)

式(1)中的变量可由下列各式求得

The ZnS films were deposited at different RF powers(100, 150, 200, and 250 W) during the same deposition time 75 min, and Ar: 10−2 mbar gas pressure. The different deposit parameters are summarized in Table 1.

(3)

qv=arcsin((yT-y)/RTM)

(4)

qh=acrtan[(-zT+z)/(xT-x)]

(5)

(6)

(7)

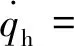
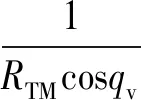
(8)

2.2 指向误差角

假设理论遭遇时间为tgo，则遭遇点在弹目视线坐标系中的矢量表达为

A=

(9)

由于期望的导弹速度指向遭遇点，则有

|A|=Vtgo

(10)

可解得tgo。理论遭遇时刻导弹的实际位置矢量为

(11)

零过载脱靶量为

σZEM=|B-A|

(12)

进而可得初始指向误差

(13)

2.3 测角误差

(14)

式(14)中，BN为等效噪声带宽，τc为距离波门宽度，S/N为接收机输出端的信噪比，fr为重复频率，βn为伺服系统带宽，θ0.5为天线波瓣的半功率波瓣宽度。

由于信号强度与距离呈4次方关系，因此，测角精度与探测距离呈1/2次方关系，可以定义测角精度均方差为

σ=kσRTM2

(15)

可见，不同的测角精度对应了不同的系数kσ。给定kσ，即可得到测角误差随弹目距离变化的模型。例如，已知1km位置的测角精度，则可求得随机一条弹道对应的误差系数

(16)

式(16)中，λrand为正态分布随机数。测角误差σv(t)、σh(t)可由下式计算

σv(t)=kσvRTM2(t)σh(t)=kσhRTM2(t)

(17)

2.4 探测盲距

当弹目距离小于探测盲距Rmin时，目标丢失。此时，弹目视线角不再更新，视线角速度保持或外推。由于测角误差、视线角速度延迟、弹体响应延迟等因素的影响，比例导引末段的视线角速度呈发散状态。一般情况下，视线角速度外推略优于保持。因此，当进入盲区，目标丢失后，视线角速度可采用线性外推方式。

2.5 视线角速度延迟

在2.1节中，通过数学运算，可以得到弹目视线角速度。但在实际情况中，导引头在获取视线角速度时存在一定程度的滞后现象。按照跟踪回路解耦设计，视线角速度可通过导引头测量的目标视线角进行提取，关系式如下

(18)

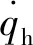
2.6 导弹运动方程

在进行末制导精度分析时，可以假设导弹和目标均为质点，导弹运动可由质点运动方程描述

(19)

过载响应方程为

(20)

式(20)中，Tm为弹体时间常数，ξm为弹体阻尼系数，km为弹体增益，B1为气动时间常数，kP、kacce、ωI、kgyro为三回路驾驶仪的设计参数，g为重力加速度。为了简化输入，可将过载响应方程写为

(21)

式(21)中，T1和T2分别为系统的两个等效时间常数，ξ为系统的等效阻尼，z向过载响应方程与y向一致。

3 数值分析

为了分析初始指向误差、导引头测角精度、探测盲距、导弹过载等因素对制导精度的影响，可根据第2节的模型进行数值仿真。基本仿真条件如表1所示。

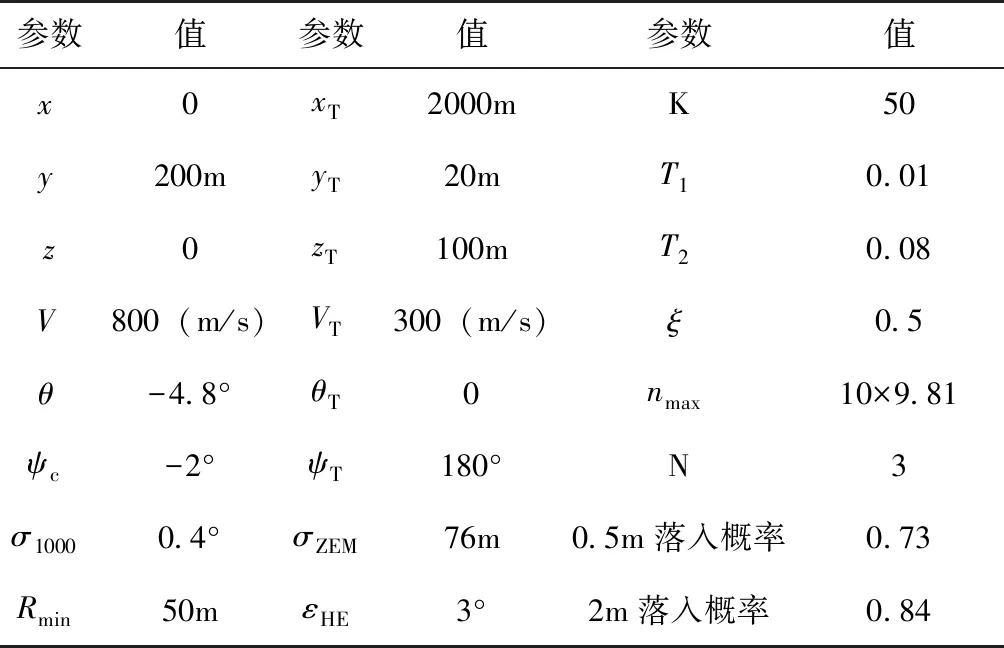
表1 仿真参数表Tab.1 Simulation parameters

从表1可以看出，在给定条件下，初始指向误差为3°。由100条随机弹道仿真计算得到的脱靶量情况如图1和图2所示。图中，红色圆半径为0.5m，蓝色圆半径为2m。可见，0.5m落入概率为0.73，2m落入概率为0.84。

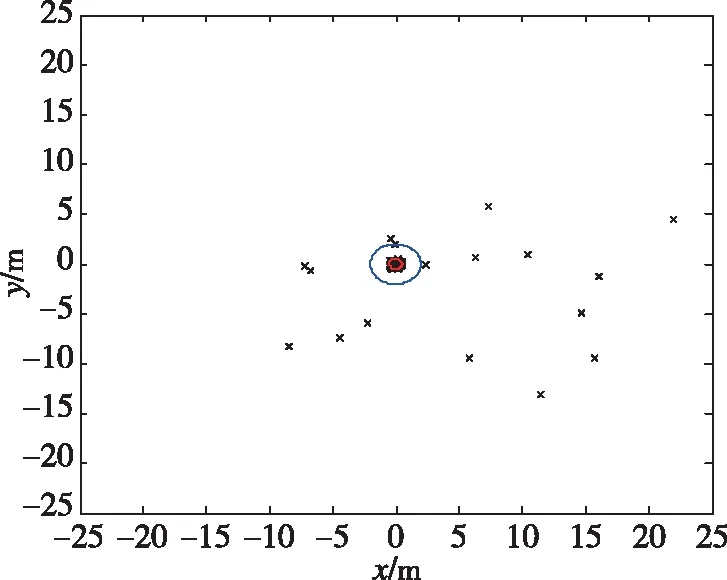
图1 100次随机仿真脱靶量分布Fig.1 Miss distance distribution for 100 random simulation

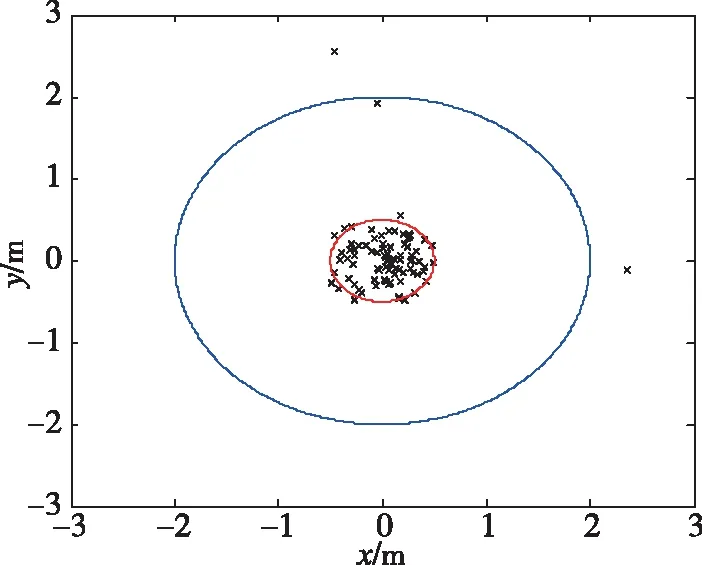
图2 100次随机仿真脱靶量分布(放大图)Fig.2 Miss distance distribution for 100 random simulation(enlarged view)

脱靶量随测角精度和探测盲距的变化曲线如图3所示(在初始指向误差近似为0的情况下)。由图3可以看出，在目标丢失后、采用视线角速度外推的情况下，探测盲距对脱靶量的影响很小；而主动雷达导引头的测角精度对脱靶量的影响很大。由测角精度随弹目距离的变化公式也可看出，测角精度一方面导致初始指向误差变大，另一方面，由于其随探测距离变化，相当于叠加了一个额外的视线角速度，这导致需用过载增加，脱靶量增大。

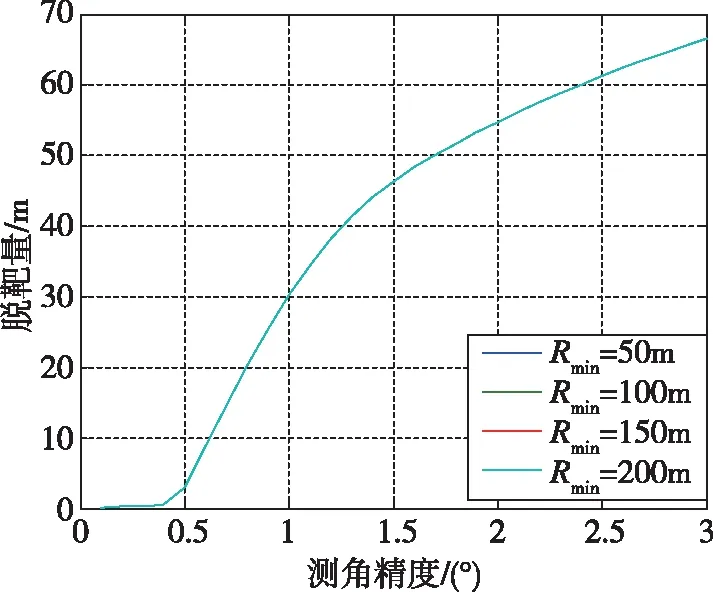
图3 脱靶量随测角精度和探测盲距的变化曲线Fig.3 Miss distance curve with angular accuracy and minimum detection range

脱靶量随指向误差和导弹过载的变化曲线如图4所示(在不考虑测角误差的情况下)。由图4可以看出，初始指向误差与最大可用过载直接相关。在给定过载条件下，初始指向误差大于某一值，会使得脱靶量急剧增加。

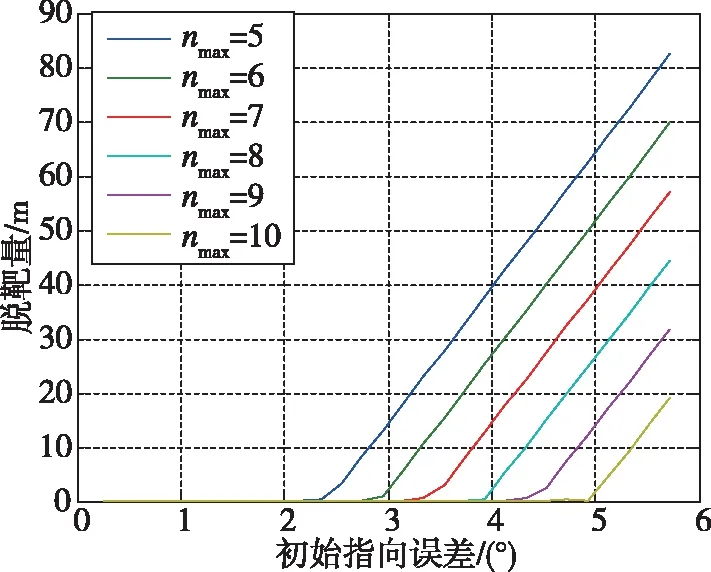
图4 脱靶量随指向误差和导弹过载的变化曲线Fig.4 Miss distance curve with heading error and available acceleration

4 结 论

本文提出了一种基于物理模型的制导精度快速评估方法，建立了主动雷达制导导弹比例导引各环节的数学描述。通过数值方法，给出了制导精度随主要影响因素变化的规律：(1)探测盲距对制导精度的影响较小；(2)测角误差从两个方面影响着制导精度。一方面直接形成了初始指向误差，另一方面导致出现了额外的视线角速度，因此对制导精度的影响显著；(3)初始指向误差与最大可用过载直接相关。在给定过载条件下，必须严格限定初始指向误差。根据本文提出的方法，在给定条件下可直接通过计算得到对制导精度影响因素的定量分析结果。