基于FPGA的红外目标识别神经网络加速器设计*

黄家明，陈 寰，史庆杰，陈海宝

(1.上海交通大学 电子信息与电气工程学院·上海·200240； 2.上海航天控制技术研究所·上海·201109)

0 引 言

红外目标识别系统在军事和民用领域中有着广泛应用。在军事领域，智能化红外目标识别系统已成为现阶段和未来武器系统的重要组成部分，是制导武器变得更加精确、更加智能的一个重要标志，也是成像制导和高分辨率武器设备中的一项关键技术；在民用领域，红外目标识别已经是自主机器人、防碰撞车辆等智能化系统中的一项重要功能。因此，对智能化红外目标识别系统进行研究，具有重大的实际意义。

国内外传统的红外目标识别采用实效性较强、基于特征融合匹配的统计模式识别方法，但该类算法在红外目标运动特性变化较快和红外目标过小等情形下，无法有效识别目标。基于深度学习的目标识别算法和架构设计是近年来计算机视觉领域中的研究重点。深度学习模型在训练时能够借由反向传播的方式对网络权重进行更新，使其能够学习提取目标特征的方式。卷积神经网络不需要由人工设置特征，模型在训练时，通过设计好的模型可直接从图像中提取所需要的特征，来进行目标识别。这种方式能够提高特征质量，进而极大地提高目标识别精度。相比于人，机器提取特征更加迅速、更加准确。得益于GPU强大的算力支持，学者们提出了数种基于卷积神经网络的目标识别算法，如SSD[1]、faster R-CNN[2]和YOLO[3]算法等。YOLO算法使用单个网络即可同时预测出物体的位置和种类，因而在准确率和执行速度之间达到了更好的平衡。本文提出的红外目标识别算法即基于YOLOv3-Tiny而实现。

在实际生产和应用中，大规模部署YOLO等卷积神经网络的一大挑战是，神经网络具有庞大的计算需求和存储要求。现代卷积神经网络的训练和推理几乎只能在CPU和GPU集群上实现，但其仍面临着能效低、耗能高的问题，这些因素对在低功耗应用领域中(如无人机或嵌入式平台)部署神经网络是至关重要的。针对上述两个问题，学界提出了数种基于FPGA的硬件解决方案[4-7]。然而，FPGA和GPU平台在计算性能上依然存在巨大差距。

许多先前的工作表明，深度学习的网络模型通常具有很大的冗余[8-10]，压缩深度神经网络的方法大致可以分为五类：参数剪枝、参数量化、低秩参数分解、卷积核压缩变换、知识蒸馏。参数剪枝的关键在于移除模型中冗余或不重要的参数，而参数量化则集中于压缩权重的占用空间(例如从浮点数压缩为定点数或整数)；低秩分解使用矩阵或张量分解技术，可将一个较大的卷积核分解为几个较小的卷积核，从而减少参数存储所需的空间。基于紧凑型卷积滤波器的方法依赖于巧妙设计的结构性卷积滤波器，从而可减少存储和计算的复杂度；知识蒸馏的方法尝试提取一个更加紧凑的模型，来产生和一个更大的网络同样的输出结果。其中，参数量化是一种常用且具有前景的深度神经网络压缩方法。特别是当将量化精度限制在低比特时，相比浮点形式的存储，权重和激活值的比特数将同时减少，从而可大大节省模型在硬件平台运行时所需的存储占用。除此以外，在低比特量化下，卷积神经网络中繁琐的矩阵-向量乘法操作可以由轻量级的位操作或查找表替代，这些位操作在嵌入式处理器和FPGA上可以达到媲美GPU的峰值性能。因此，与其他网络压缩方法相比，低比特量化具有极小的内存占用、高能效、高加速比的硬件友好特性。基于低比特量化，本文提出了一种充分利用硬件计算资源的FPGA神经网络加速器。

1 YOLO卷积神经网络

YOLO卷积神经网络通常包含几个基本层：卷积层、批归一化层、激活函数、最大池化层、上采样层和路由层。考虑到YOLO是一个单步神经网络，其能够同时预测目标的位置和种类，所以全连接层不在本文的讨论范围中。卷积层用于从输入图像中提取高维特征，卷积神经网络中的卷积层的操作如下式所示

x-1,j+y-1,l)

(1)

式(1)中，wn表示第n层的权重；an-1表示第n层的输入特征值；K为卷积核的宽度；on表示第n层的输出；x、y、z用于定位三维张量on中的某一元素；i、j、l、z用于定位四维张量wn中的某一元素。为了简化公式，略去偏置项，假设卷积运算的步长为1。最大池化层对输入的特征图通过K×K的滑动窗口进行池化。与卷积层不同，这些滑动窗口不会相互重叠，其输出的特征值在宽度和高度上均可缩小为输入的1/K，从而达到减小中间特征值尺寸的目的。可通过在YOLOv3-Tiny中引入上采样层来改善对不同尺寸目标的识别准确率。采用上采样层的最初目的是放大输入图像，以便它可以在更高的分辨率下实现显示。YOLOv3-Tiny采用非线性插值方法——在像素之间插入0，使得输入的图像在宽度和高度两个维度上扩大为原来的2倍。

批归一化层被广泛应用于现代卷积神经网络的训练，它可以帮助训练快速收敛并有效防止网络模型过拟合。在进行批归一化后，前一个卷积层输出的内部偏移减少，并呈现正态分布。批归一化层的操作如下式所示

(2)

式(2)中，x、y分别表示批归一化层的输入和输出。μ(i)、σ(i)分别为一批中特征图在第i个通道的平均值和方差，γ(i)和β(i)是批归一化层中两个可学习的通道级参数，ε用于避免数据溢出。在神经网络的前向推理过程中，所有的参数将被固定并参与运算。在未被进一步优化前，FPGA在实现上述运算时会面临巨大的计算开销和额外的片下存储访问。

为了增强神经网络的表达能力，解决线性不可分问题，通常可在两级卷积层之间加入非线性函数，该函数被称为激活函数。常见的激活函数有Sigmod函数、Tanh函数和ReLU函数。其中，ReLU函数可用下式所示

(3)

式(3)中，R(x)为ReLU函数的输出。由式(3)可以看出，ReLU函数起到了线性整流的作用，其只需一个比较器即可在硬件平台上实现，运算速度快。因此，YOLO网络采用ReLU函数作为激活函数。

为了获取神经网络前半部分提取到的特征，路由层将会级联两个具有相同尺寸、来自不同卷积层的输出特征值。由于路由层仅在通道这一维度上对两个特征图进行拼接，可以将待拼接的两个特征图连续存放在片下存储器中。路由之后的卷积层无需额外操作，便可直接读取拼接后的特征值。

设计采用的YOLO模型为YOLOv3-Tiny，是YOLOv3的简化版本，具有更少的存储空间和计算开销，适合部署在资源有限的嵌入式设备上。YOLOv3-Tiny接收一张尺寸为416×416的图片作为输入，分别在13×13、26×26两个不同尺度的网格划分中给出预测结果。每个网格会生成三个预选框。每个预选框具有五个预测数据，分别为预选框中心在网格中的横、纵坐标，预选框的宽和高，以及置信度。置信度可分为识别位置置信度与种类预测置信度。图1展示了YOLOv3-Tiny的数据流。

图1 YOLOv3-Tiny数据流图Fig.1 Data flow of YOLOv3-Tiny

2 卷积神经网络低量化

2.1 可变缩放因子

得益于GPU强大的浮点运算能力，当前的卷积神经网络通常将权重、偏置、激活值和梯度用浮点张量形式进行存储及计算。当在其他硬件设备上进行神经网络的部署时，量化成为了减少硬件存储和节约硬件资源必不可少的环节。量化将模型参数和激活值近似为一系列分立的值，来减少表征时所需的比特数。本设计采用了均匀量化方式，其中近邻量化点之间的距离相等。在给定量化位宽k时，量化过程Qk可表示为

(4)

式(4)中，xr为张量，可为权重、偏置或激活值；α为缩放因子；q为在整数运算单元中参与计算的整数张量；xq为量化后的参数，用于网络训练。缩放因子α对于低比特量化而言至关重要，卷积神经网络中的权重分布存在长拖尾，选择合适的缩放因子α变得尤为困难。具体而言，如果α过小，较大的权重会被钳位；α过大，会导致大部分的权重量化到同一个值，这两种情况都会造成严重的量化误差。同时，权重分布在不同层甚至不同通道间，存在较大的差异。预先设置的α无法达到最优的量化效果。

为了解决上述问题，引入了一个在训练中可学习的缩放因子α，来实现量化区间可变的量化过程。式(4)中的量化过程可修正为

(5)

为了能够在神经网络训练中更新缩放因子α，需要计算反向传播时α的梯度。由文献[11]可知，α的梯度可表示为

(6)

2.2 批归一化层融合

正如在第一节中提到的，将批归一化层合并到前一个卷积层中，可以减少额外的计算开销和片下内存访问，从而减少神经网络前向推理的延迟和功耗。在前向推理阶段，批归一化层的参数是固定的，式(2)可改写为

(7)

式(7)中，o为前一卷积层的输出，量化后的卷积操作可表示为

(8)

式(8)中，αa、αw分别为全精度输入激活值ar和全精度权重wr的量化区间；qa和qw分别为在量化过程中产生的输入激活值整数张量和权重整数张量；ξ和η分别为ξ(i)与η(i)在通道维度上的向量形式。显然，批归一化层可以与卷积层进行合并，合并后的量化卷积过程如下式所示

(9)

与常见的均匀量化方式相比，上文提出的低比特量化算法主要将缩放因子α改进为在训练中可更新的参数，并提出了有效的梯度生成策略。该方法不涉及神经网络的训练方式与优化方法的选取，无需进行特定修改即可被延伸至其他基于卷积神经网络算法的量化压缩中。

3 FPGA加速器架构设计

3.1 卷积单元基础架构

为了提高FPGA加速器的计算性能，多数设计采用全流水线架构，即对一个网络中的所有卷积层分别进行优化设计，使每个卷积层各自使用其计算单元与存储单元，从而实现高并行度、高吞吐率。然而，此类加速器实现所使用的FPGA均需要消耗大量的硬件资源且价格昂贵、能耗较高，无法满足嵌入式使用场景的低功耗要求；所进行的全流水线优化的数据流架构设计虽然吞吐率高、计算性能强大，但设计的可拓展性不高，无法跨网络或跨硬件平台实现。

本设计选用YOLOv3-Tiny——一个轻量级的神经网络，作为FPGA加速器的部署目标，并实现了低比特量化。但是，由于嵌入式FPGA的硬件资源有限，无法将模型权重和由每一层产生的激活值全部存储在片上，实现层与层之间完全的流水化。为了充分利用硬件资源，沿用文献[5]提出的设计思路，使用同一个卷积计算单元执行网络不同层所需的计算任务。卷积计算单元的内部是一个高度并行的计算核心，用于完成神经网络中核心的乘加运算。整体架构可用于计算不同参数配置下的卷积层和池化层，在只需要修改部分参数的前提下，即可用于加速其他基于卷积神经网络的目标识别或图像分类算法。

神经网络中的卷积计算，实质上是如式(1)所示的六层嵌套循环。对卷积计算的加速优化，实际上是对此卷积循环的并行优化。在卷积计算单元的设计中，需要在合适的维度进行并行，在尽可能高的资源利用率前提下，实现理想的加速效果。为了提高卷积层中权重和输入激活值的数据复用率，该设计采用了一系列循环变换优化方法(如循环重排、分块和展开等)对卷积循环进行优化，减少片上所需空间，并提高吞吐率。优化后的卷积循环已广泛成为FPGA神经网络加速器的基本设计思路。应用文献[5]所提出的优化方法，式(1)中的卷积操作可以变换为图2中的伪代码。

其中，数组I、O、W分别代表输入激活值、输出激活值和卷积核权重，存放在片下DRAM；Ibuf、Obuf、Wbuf分别为FPGA片上输入缓存、输出缓存和权重缓存，用片上存储单元进行存储。此处忽略掉卷积层中的偏置，因为该参数的数据量较少，可以全部存储在片上；N为输入激活值的通道数；M、R、C为输出激活值的通道数、宽和高；K为卷积核的大小；S为卷积窗口的滑动步长，一般为1。其中，Tr、Tc、Tm、Tn分别为循环R、C、M、N的分块系数，决定了片上缓存的大小，循环顺序决定了在何时发生片上和片下数据的交换。伪代码中第1行到第6行的数据交换发生在FPGA与嵌入式CPU之间，表示FPGA端从片下DRAM中读取所需数据到对应的片上缓存；第7行到第16行操作在FPGA片上执行，对读取的数据进行卷积操作，产生的输出暂存在片上；第17行到第18行操作将一部分卷积结果写回片下DRAM。最内层的两个循环完全展开并进行流水线处理，伪代码所描述的卷积计算单元如图3所示。

图2 变换后的卷积循环伪代码Fig.2 Pseudocode of transformed convolutional layer

图3 两层循环展开卷积计算单元Fig.3 Convolutional compute engine with two unrolled loops

如图2中的伪代码所示，卷积循环在输出和输入激活值通道数M和N两个维度部分展开，建立的计算单元需要Tm×Tn个乘法器和Tm个加法树，可流水地处理乘加运算。其中，Tm、Tn分别为输出和输入并行度。图3展示了图2伪代码中第7行到第10行循环中，循环变量tr=4、tc=2、i=1、j=2时刻两层展开卷积计算单元的状态。流水线完全建立后，在一个时钟周期内，卷积计算单元从Tn个独立的输入缓存中各读取一个相同位置的特征值，同时读取对应通道的Tm×Tn个权重。Tm×Tn个乘法器重复利用Tn个输入像素与对应权重进行乘法运算，Tm个加法树对乘积结果两两相加，得到的结果与部分和累加后，写入Tm个独立的输出缓存中。该卷积计算单元的设计主要利用乘法器与加法器，在FPGA中主要利用数字信号处理单元(Digital Signal Processing，DSP)进行实现。其中，32位浮点加法需要2个DSP，32位浮点乘法需要3个DSP。16位定点量化后的一次乘加运算只需要1个DSP。与浮点数相比，使用定点数减少了硬件资源的消耗。在允许的精度损失内，定点计算具有更高的峰值性能。该架构无需修改，即可用作低比特卷积运算单元。但是，对于低于16位整数的乘加计算而言，1个DSP在每个时钟周期内依然只能完成一次乘加操作，无法充分发掘低比特量化的计算潜力。为了实现更优的计算性能，需要在其他卷积维度中寻找并行度。

3.2 卷积单元模型分析

对于一个给定的卷积层，图2中伪代码描述的卷积模型所需的总共执行周期C、计算性能P及所需带宽B为

(10)

(11)

B≈

(12)

由式(10)、式(11)、式(12)可知，给定系统时钟频率及所需运行的卷积层结构，该加速器架构的计算性能及所需的带宽便可被预估。同时可以看出，提高该架构计算性能的关键在于分块系数Tm、Tn。但是，提高Tm、Tn会等比例地增加所需带宽。由于需要使用双缓存来减少计算单元的数据传输等待时间，输入缓存、参数缓存和输出缓存所需的片上存储的个数将会增大为原来的2Tm、2Tn倍，且每个DSP所能够执行的乘加次数没有改变，板上计算资源的利用率并没有获得实质提高。

3.3 多维度并行卷积单元

为了充分发掘低比特卷积计算的计算潜力，将图2中卷积循环的四个最内层循环全部并行展开，使得此时卷积单元在每个周期内需要从Tn个输入缓存中分别读取K×K个输入激活值，然而用于存储输入缓存的BRAM在每个时钟周期内仅支持一次对于不同地址的读操作。为了解决单周期内多个读操作的冲突，可引入在视频处理中常用的行缓存和滑动窗口缓存。可将卷积计算过程看作一个固定大小的卷积窗口在输入激活值附近滑动，并对窗口内的激活值与对应权重进行乘加计算。由于近邻的滑动窗口经常重叠，从输入缓存中读取的激活值具有空间局限性，可以再次进行局部缓存，并多次访问。该局部缓存又被称作行缓存，因为它的功能是用来存储输入激活值中的一个滑动窗口周围的行，并通过片上存储进行实现。滑动窗口缓存则使用触发器(Flip-Flop，FF)进行实现，窗口内的每个数据彼此独立存储。多维度并行卷积单元依然可以采用3.2节中的模型进行定量分析，所需的总共计算周期、计算性能与所需带宽为

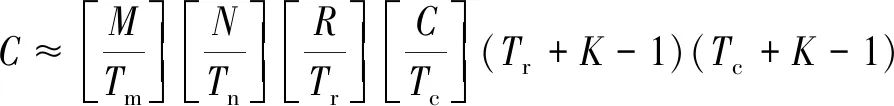
(13)

相比文献[5]中的设计，多维度展开后，卷积单元在3×3的卷积层中可以获得接近9倍的性能提升，所需带宽仍然等比例增加，但片上存储只需要额外Tn×(K-1)个片上存储单元用于行缓存。借助滑动窗口设计，卷积计算单元可在每个周期内从Tn个输入缓存中分别读取K×K个输入激活值。由于卷积层权重进行了低比特量化，每个权重存储仅需两个比特，使用一个32比特的数即可存储一个3×3卷积所需的九个权重。将图3中的输入缓存改为滑动窗口缓存，不再单独读取一个权重，而是直接读取九个权重，单个乘法器替换为一个处理单元(Process Element，PE)。图4为图2伪代码中循环变量tr=2、tc=4时刻四层循环展开卷积计算单元的状态。

由图4可以看出，卷积计算单元的整体结构没有发生变化，依然使用加法树对中间结果进行不断累加，最终存储在输出缓存上。改动较大的部分发生在原本的乘法器上，单个乘法器无法在一个周期内完成九个乘加操作，需要设计PE来实现其功能。

一个PE中包含九个乘法器和一个由九个加法器组成的加法树。由于权重量化到两个比特，输入激活值量化到八个比特，乘加操作可能产生的结果数大大减少，实现该功能的电路相对简单。在150MHz条件下，该电路满足时钟约束，这意味着该PE可在一个时钟周期内完成九个乘加操作。由Vivado HLS—Xilinx的FPGA设计仿真综合工具产生的综合结果可知，该PE可由五个DSP组成。相比于只展开两层循环的卷积单元，每个DSP能够完成的等效乘加操作从1提高到了1.8，DSP的利用率提高了80%。图4中最上方PE的状态如图5所示。

图4 四层循环展开卷积计算单元Fig.4 Convolutional compute engine with four unrolled loops

图5 卷积计算单元中的PE架构图Fig.5 PE in convolutional computing engine

3.4 卷积-池化级联加速器架构

FPGA加速器采用如图6所示的卷积-池化级联加速器架构，其整体是一个嵌入式CPU+FPGA的异构系统，CPU负责控制片下数据的传输，并向FPGA发送控制指令。FPGA包含了卷积、池化、非线性激活函数三个计算单元，输入缓存、输出缓存和参数缓存均采用双缓冲设计，以免计算单元因等待数据传输而停顿。控制单元负责解码CPU发送的控制指令，调度片上数据传输和计算。传输总线则负责片上缓存与片下存储的数据交换。

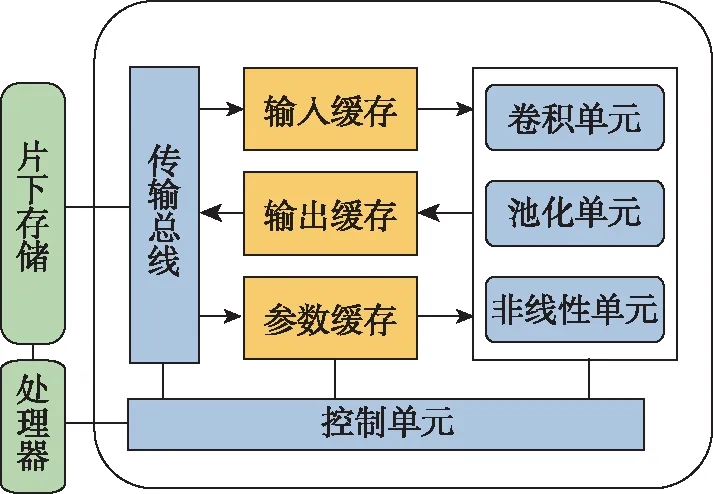
图6 卷积-池化级联加速器架构Fig.6 Architecture of convolutional-pooling cascaded accelerator

池化单元并不执行直接的数据计算，但依然存在大量的片上和片下数据交换，而数据交换影响着系统整体的延时与功耗。考虑到每隔N/Tn个卷积计算周期才会发生一次对片下存储的写入操作，且每次写入的特征值均满足池化操作的执行条件，因而池化操作可以紧跟卷积之后，以流水线的方式进行，而不需要作为一个单独的模块。该流水线需要额外的片上存储单元来对池化输出进行缓存，缓存的大小与输出缓存相当，这样的调度只会影响输出缓存写回时的所需带宽，该带宽如式(14)所示

(14)

由于分块系数Tn通常远小于每个卷积层输入特征值的通道数N，由级联架构带来的额外带宽不会影响系统的整体计算性能。

4 设计结果分析

4.1 网络量化结果分析

使用 Pytorch 神经网络框架实现低比特量化YOLOv3-Tiny的训练与测试。数据集使用自建红外小目标，由人工标注数据集。数据集中只有一类物体，但一张图片中出现的物体大小与数量不尽相同。其中，训练集含有794张图片，测试集含有248张图片。

低比特神经网络的建立需要多轮训练。首先，使用全精度浮点形式从零开始训练网络至收敛；随后，对卷积层做低比特量化处理；然后，对卷积层和紧邻的全精度批归一化层进行融合，并再次量化；最后，对量化时的缩放因子进行比特移位量化。表1给出了YOLOv3-Tiny在红外数据集上量化后的精度，最终FPGA板上平均准确率(Mean Average Precision，mAP)损失控制在了7.1%。三类不同大小、不同数量的红外目标识别结果如图7所示。得益于本文提出的在训练中可变的缩放因子，可以看出，在权重限制在两个比特的情况下，对不同场景下的红外目标仍能提供准确的预测结果。

表1 YOLOv3-Tiny量化结果Tab.1 Quantization results of YOLOv3-Tiny

(a) 第一类场景

(b) 第二类场景

(c) 第三类场景图7 红外识别效果图Fig.7 Result of infrared object detection

4.2 FPGA加速器性能分析

在PYNQ-Z2开发板上对所提出的加速器进行部署与评估。PYNQ-Z2使用了一款低成本的Xilinx Zynq-7000 SoC，内含XC7Z020 FPGA芯片和ARM Cortex-A9嵌入式处理器，开发板提供最高25.6(Gbit/s)的传输带宽。使用Vivado HLS 2018.2进行加速器的设计和编译。在硬件资源和带宽的限制下，选择分块系数Tm=8，Tn=4，Tr=26，Tc=26。此时，FPGA的DSP和LUT硬件资源利用率均在90%以上，说明主要用于卷积计算的硬件资源已充分利用。由于网络中的每一卷积层需要等待前一卷积层完成计算才可以运行，YOLOv3-Tiny中每个卷积层所需的计算量和达到的计算性能可以进行独立的评估。

如图8所示，第12个卷积层达到了90.6GOPS的峰值性能，平均性能为65.6GOPS。其中，第8、10、11和13层的卷积核大小为1×1。当卷积核大小为1时，式(12)中的计算性能将会退化为式(10)。四层循环展开后，卷积单元的性能与两层展开相当。卷积核大小为1×1，计算量不到YOLOv3-Tiny整体计算量的2%，所以其对加速器整体计算性能的影响有限。由于采用了卷积-池化级联加速器架构，节省了池化层所带来的能量消耗，最终系统的功耗为2.6W。文献[12-15]提出的YOLO加速器的峰值性能分别为10.5GOPS、62.9GOPS、86.4GOPS及48GOPS。与之相比，本文提出的加速器达到了最高的峰值性能，在运行第12个卷积层时达到了90.5GOPS。Zynq YOLO[14]的板上DSP硬件资源利用率达到了100%，但由于参数均采用了8bit的定点量化，每个DSP仅能提供1次乘加运算，最终的峰值性能为86.4GOPS。本文提出的PE充分利用了低比特量化带来的计算优势，每个DSP能够等效地提供1.8次乘加运算，在保证高的DSP资源利用率的前提下，实现了更高的峰值性能。

图8 YOLOv3-Tiny卷积性能对比图Fig.8 Comparison of convolutional layers’ performance in YOLOv3-Tiny

5 结 论

本文提出了低比特量化的YOLOv3-Tiny算法，在对于不同数量、不同大小的复杂场景下的红外目标的识别任务中，当权重量化至两个比特时仍保持了高识别率，并在PYNQ-Z2 嵌入式FPGA开发板上进行了加速器实现。本文提出了在网络训练中可更新的量化区间及相应的梯度生成方式，解决了在传统量化过程中选取最优量化区间的难题，在低比特量化条件下取得了优异的压缩效果。在原理上，在无需改变量化算法与FPGA加速器架构的前提下，即可拓展至各类目标识别任务及多分类任务的卷积神经网络中。得益于低比特量化，所提出的神经网络加速器所需带宽大幅降低，即使增大并行度，每个时钟周期内的数据交换次数增加，仍能保证系统在150MHz的工作频率下运行；同时，采用行缓存和窗口缓存实现了滑动窗口处理方式，大幅提高了卷积计算的并行度，达到了90.1GOPS的峰值性能。与其他相关工作相比，本文提出的FPGA加速器具有优异的能效表现，为嵌入式红外目标识别系统提供了一种能效高、识别精度高的解决方案。