基于多尺度数据挖掘的数据尺度划分方法

张煜睿

（吕梁学院计算机科学与技术系 山西省吕梁市 033099）

大数据时代中每天都会产生海量的数据，如何有效地提取这些数据中的有效成分，并根据这些信息得到正确的决策，成为了计算机行业研究的重点内容。数据尺度划分是一种监督式的学习方法，通过分析已经确定类别的训练数据集的分布特征，构建其潜在分类模型，最后对新数据进行划分。在对计算机网络大数据的研究中，数据尺度划分占据着重要的地位，是一切大数据分析和决策的基础[1]。当前对于数据尺度层级划分的研究中，已经有了很多成功的经验，例如基于多尺度关联规则的数据尺度划分方法、基于多尺度聚类的数据尺度划分方法等,但是这些数据划分方法在精确度和算法冗余度上都存在一定的缺陷。因此本文提出了基于多尺度数据挖掘方法，以求弥补传统方法的不足之处。

1 多尺度数据挖掘方法研究

尺度在计算机领域通常被作为一种拥有具体含义的比例尺，而多尺度则是一个具备一定顺序的多个尺度的集合Hi[2]。因此可以对其进行定义：若H1与H2是相邻尺度，且满足则可以称H1是H2的父尺度；若H1与H2是相邻尺度，且满足则可以称H1是H2的子尺度；若H1与H2是是不相邻尺度，且满足则可以称H1是H2的子孙尺度；若H1与H2是不相邻尺度，且满足则可以称H1是H2的祖先尺度。例如，若构建一个某市全体中小学生数量的数据集，且在这一数据集中拥有五个尺度，则可以称班级是学校的子孙尺度，班级是年级的子尺度。

而多尺度数据挖掘是一种能够将具备多尺度属性的信息数据作为研究对象，并对其进行一定的处理的数据操作方法[3]。在使用多尺度数据挖掘方法处理数据时，首先需要预处理，使计算机中的数据形成一个具备多尺度特征的数据集。在多尺度数据挖掘的引导下将这些数据集中的隐含信息推导出来，形成一个特征点，并将这些尺度扩散到其他信息尺度中。

2 数据尺度划分方法设计

2.1 构建多尺度数据集

在构建多尺度数据集之前，首先需要根据上文所述的多尺度定义研究将数据集多尺度化的方法，然后才能够根据所得到的尺度熵构建多尺度数据集。

数据集多尺度化的时间复杂度呈现循环嵌套的结构，数据集多尺度的划分呈现了各数据属性的尺度特征，并为后续的研究提供了一个测量方法，在之后的研究中，很有可能导致数据复杂程度的变化，进而影响数据熵的变化[4]。从另一个角度，数据熵也可以作为一种检测数据多尺度的评价方法，通过对于数据尺度特征的寻优，构建多尺度数据集。在构架多尺度数据集时，不仅需要考虑尺度特征的复杂性，也需要确定数据尺度划分后的数据熵的大小，因此可以对数据熵进行定义，其公式如下所示：

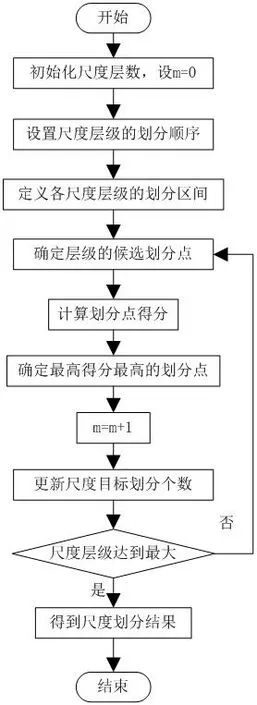
图1：数据尺度划分方法算法流程

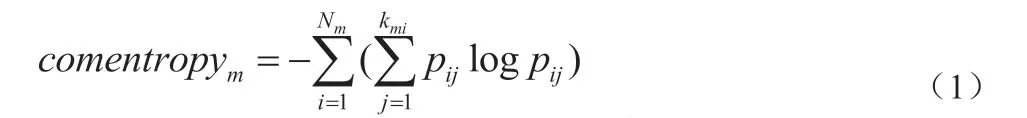
式中，m 表示信息熵的尺度层次；pij表示第id 个层级中数据j出现的概率；Nm表示数据划分的第m 层中所具备的划分块数[5]。因此可以得知，在构建多尺度的数据集时，选择数据熵的尺度越高，其数据集建立的覆盖度就会越大。

2.2 标签数据的基准尺度选择方法设计

本文基于多尺度数据挖掘的数据尺度划分方法以标签数据的基准尺度的最优选择方法为实现数据尺度划分的依据，通过上文中对于数据集的构建过程，可以得到设计标签数据的基准尺度选择方法。

表1：实验结果

2.3 数据尺度划分方法研究

首先需要依据上文中的标签数据的基准尺度选择方法确定数据尺度的模型及其对于尺度特征属性的划分。通过迭代的方式，将数据集中的范围尺度、粒度尺度进行划分，例如可以将中小学的“年级”划分为“一年级”、“二年级”、“三年级”、……、“九年级”等。因此可以得到其算法流程如图1所示。

通过上述算法流程划分数据尺度，对输出的m 层尺度划分结果进行计算，并通过公式（1）得到其数据熵。在该类数据尺度划分的计算中，可以通过迭代法不断循环计算，直到尺度层级达到最大。

3 实验设计

3.1 实验准备工作

本实验采用对比实验的方法，需要首先在计算机上设置一个虚拟环境，其实验环境参数如下：CPU 为Intel Xeon E5-2690 v3 i7-6700 2.6GHz、8GB 运行内存、Windows 10 操作系统、MS SQL Server 2012 数据库。

本实验中以某市全体中小学生的数量作为数据集，同时以IBM T10I4D100K 数据集作为辅助，验证上表中各开发程序及MSARMA算法的准确性。在某市全体中小学生数据集中，学生的户籍所在地以及所在学校、班级十分完整，其属性可以形成一个具备多尺度的概念分级。在这个数据分级中，将班级内的学生数作为最初级的尺度，将所有一年级至九年级的学生都纳入到数据集中。为了保证实验结果的准确性，该实验需要反复进行5 次，最后计算5 次实验结果的平均值。

3.2 实验评价指标

在本实验中，为了验证本文提出的基于多尺度数据挖掘的数据尺度划分方法的有效性以及对比其他方法的优越性，对其与基于多尺度关联规则的数据尺度划分方法、基于多尺度聚类的数据尺度划分方法进行对比实验。将算法的覆盖率、精确度以及该算法的执行时间作为评判依据。

3.3 实验结果分析

将5 次试验的结果通过Matlab 软件进行整理和分析，得到如表1所示的实验结果。

由表1 可以看出，基于多尺度数据挖掘方法的覆盖率和精确度与基于多尺度聚类算法的覆盖率和精确度相差不大，且均大于基于多尺度关联规则算法。而执行时间的数据可以表示该算法的程序冗余度，执行时间越短，则该算法越简洁。在上表中，基于多尺度数据挖掘方法在5 个实验中的执行总时间为84s，基于多尺度关联规则算法的执行总时间为82s，基于多尺度聚类算法的执行总时间为138s，因此可以判断前两种算法的算法简洁性远远大于第三种算法。根据以上数据，本文设计的基于多尺度数据挖掘的数据尺度划分方法既能够实现覆盖率和精确度的优越性，又具备算法的简洁性，在综合评价上优于传统的两种算法。

4 结束语

本文为了能够更好地进行数据尺度划分工作，将多尺度数据挖掘引入到了该领域，提出了多尺度数据挖掘在数据尺度划分中的理论基础，使用对比实验证明了本文研究的算法在精确度和简洁性上的综合性能超过传统的数据尺度划分方法。在下一步的研究中我们还需要继续将多尺度数据挖掘继续进行尺度上推或下推理论研究，分析在数据尺度划分的过程中多尺度挖掘的变化规律，并探究进一步提高数据尺度划分精确率的方法。