基于贪心算法的棋盘覆盖着色技术

王利民 石晨阳

（河北建筑工程学院 河北省张家口市 075000）

1 引言

棋盘覆盖问题是一种常见的编程问题，它主要是指在一个2k×2k个方格组成的棋盘中，选取一个方格与其他方格不同，称为特殊方格，用4 种朝向各不相同的L 型骨牌（由3 个方格组成）对棋盘上除特殊方格以外的区域进行覆盖，且任何两个L 型骨牌不得重叠覆盖[1]。棋盘覆盖着色是通过对棋盘方格赋予不同的颜色，以增加视觉表现力的效果。

其中在教学实践中，为了形象的描述棋盘覆盖问题，通常采取的方案是对L 型骨牌赋予不同的颜色。但是该算法存在着下列弊端：

（1）当棋盘方格众多时，对颜色数量的需求较多，导致界面整洁度较差。

（2）两个相邻的L 型骨牌的颜色接近导致界面的显示效果不直观。

为了有效的解决棋盘覆盖着色问题存在的上述弊端，需要对棋盘覆盖着色算法进行研究。为此，本文提出了基于贪心算法的棋盘覆盖着色技术，将其与现有的算法结合起来，利用3 种颜色实现棋盘覆盖的着色，以达到直观简洁的显示效果，并使该问题在教学实践中能够更加直观的展示可视化界面。其独创性主要表现在利用有限的颜色清晰的展示棋盘覆盖的问题。

2 实现原理

2.1 棋盘覆盖技术的基本设计思想

棋盘覆盖问题是《算法设计与分析》课程中讲解分治法的重要案例[1]，具体过程如下：

当k>0 时，将2k×2k棋盘分割为4 个2k-1×2k-1子棋盘，如图1所示。特殊方格必位于4 个较小子棋盘之一中，其余3 个子棋盘中无特殊方格。为了将这3 个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L 型骨牌覆盖这3 个较小棋盘的会合处，如图2所示，从而将原问题转化为4 个较小规模的棋盘覆盖问题。递归地使用这种分割方法，直至棋盘简化为1×1 棋盘[1]。

2.2 现有的棋盘覆盖着色技术

针对棋盘覆盖问题的着色技术一般情况下采取的解决方案是对每个L 型骨牌赋予不同的颜色，并利用当前L 型骨牌的颜色对代表棋盘方格进行着色，当k=2 时，即棋盘由22×22=4×4 个方格组成时，除特殊方格以外，还需（22×22-1）/3=5 种颜色对代表棋盘的棋盘方格进行着色，如图3，但当k ＞2 时，随着k 的增加，需要的颜色种类以幂次方增长，当k=3,除特殊方格以外还需（23×23-1）/3=21种颜色如图4，也就是说代表棋盘方格被覆盖的颜色也越来越多，且相邻的L 型方格之间的颜色也越来越相近。

尽管该解决方案能实现棋盘覆盖着色的有效性，同时也解决了图5 相邻L 型棋盘赋予相似（标注2 与3 方格）颜色的问题，但是当 k 值较大时，所需颜色众多、颜色相似等问题越发明显，也就是说棋盘覆盖的显示特性和展示效果并不明了，因此该方案需要进一步改进。

2.3 基于贪心算法的棋盘覆盖着色技术的思路

贪心算法总是做出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所做出的选择只是在某种意义上的局部最优选择。贪心算法的基本思路是从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快地求得更好的解[1]。

根据贪心算法的定义及基本思路，基于贪心算法的棋盘覆盖着色技术主要通过以下原理：

（1）将所有覆盖棋盘的L 型骨牌进行标号。

（2）判断当前L 型骨牌和周围L 型骨牌的大小。

（3）对不同的L 型骨牌依次赋值3 种不同的颜色。

3 关键程序流程图及实现

其实现流程如图6所示。

其具体实施方案如下：

（1）利用分治法完成棋盘的L 型骨牌覆盖算法，并对每个棋盘方格进行标号；

（2）按照序号将对应方格的横纵坐标保存在一个新的数组boardList[]中；

（3）根据数组首列数值确定该行是否为特殊方格（首列记录该行保存的特殊方格个数，L 型骨牌为3 个，特殊方格为1 个）；

（4）横纵坐标依次判断当前骨牌周围骨牌所存储的骨牌序号；

（5）如果周围骨牌序号比当前骨牌序号小，则保存在新的数组boardAround[]中；

（6）从0 序号骨牌开始，依次判断周边是否存在序号小于当前序号的骨牌；

图1

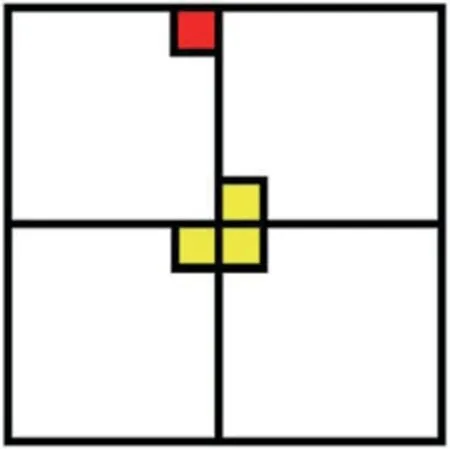
图2

图3

图4

图5

图6

图7

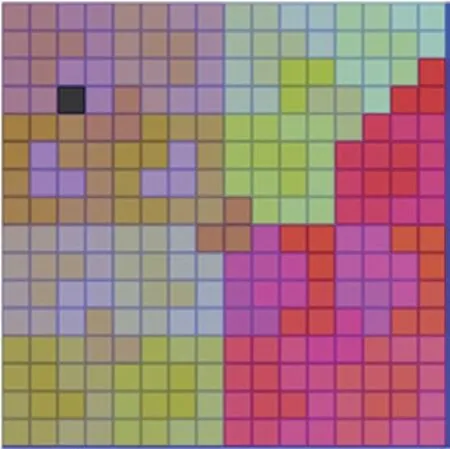
图8

图9

（7）否，则将当前骨牌对应的方格赋值为颜色1；

（8）是，则按照序号顺序依次判断当前骨牌的周围骨牌是否存在颜色1，若是，按照骨牌序号顺序将当前骨牌对应的方格赋值为颜色2，依次遍历，最终找到与小于当前骨牌次序的周边骨牌颜色不冲突的最小颜色。

该方案可以用较少的颜色显示所有骨牌，因此可以采用对比鲜明的少数几种颜色即可，实践证明棋盘覆盖问题的着色方案只需要的三种颜色即可实现，故实际选用了绿、红、蓝三色，最终图案色彩艳丽，对比鲜明。

4 实现结果与分析

为了检验本文算法的有效性，分别对现有的着色技术方法和本文提出的着色方法技术进行比较，我们设置k=4 的情形，此时当k=4 时，一共有24×24=256 个方格，除特殊方格以外还需（24×24-1）/3=85 个L 型骨牌，标号如图7所示，针对现有棋盘覆盖着色技术而言也就是除特殊方格以外还需要85 种颜色，其着色后的棋盘显示如图8所示,此时在同样的条件下，而基于贪心算法的棋盘覆盖着色方法，其显示效果如图9所示（其中为了描述特殊方格在棋盘中所处的位置，将特殊方格由绿色改为黑色，以便观察棋盘着色后的显示效果，其目的是使得整体的图形界面更加清晰）。

从图8 中我们可以看出该算法虽然能够展现棋盘覆盖问题的特性，但是其中所需的颜色数量极其庞大，同时颜色的相似性也较高，并未达到直观的显示效果，相反图9所示的结果则表明覆盖棋盘所需的颜色数量极少、且颜色对比鲜鲜明，能够直观的反应棋盘覆盖问题的特性。

4 结论

针对现有棋盘覆盖着色的技术在棋盘覆盖显示上面临的问题，深入研究了该算法的特性，并针对棋盘覆盖着色所需颜色众多和显示效果不直观的问题了提出了基于贪心算法的棋盘覆盖着色技术，最终在实践中完成了用三种颜色显示棋盘覆盖的效果，为今后研究其他类似相关着色领域奠定了基础。