后缘柔性可变形翼肋模块设计分析与试验

雷朝辉，宋 晨,2*，张桢锴，杨 超

(1.北京航空航天大学 航空科学与工程学院，北京 100191；2.北京航空航天大学 无人系统研究院，北京 100191)

1 引 言

航空业已成为世界上最大的行业之一[1]，微小的技术改进都可带来显著的经济效益。在现有条件下，传统机翼设计方法仍有诸多局限性。例如传统机翼由于安定面与操纵面之间不可避免地存在间隙，表面的刚性运动引起的曲率的离散和不连续变化引起了显著的阻力增量[2]。

自适应机翼的概念最初起源于主动变形的设计思想，而变形飞行器概念和控制装置的出现甚至早于莱特兄弟的飞机[3]。自适应机翼主要通过改变翼型的弯度，即翼型中弧线的弯曲程度来改变气动力在整个翼面上的分布，从而达到在各飞行任务环境中提高飞行效率的目的。

自适应机翼有很多优点，比如通过同步非对称偏转外翼前段和后段的活动组件改善大迎角横向操纵性；同步操作机翼弯度和水平尾翼的偏度直接控制升力；增大内端机翼弯度降低大过载飞行时的弯矩；随外界扰动变化偏转分段襟翼来降低在不平静大气中飞行时的载荷；大大降低雷达反射面积等[4]。

自适应机翼变形设计方案大致可分为3个类型，即面内变形、面外变形和翼型变形。其中，变弯度机翼的变形形式主要包括自适应变弯度前缘机翼和自适应变弯度后缘机翼两种。

关于自适应变弯度前缘机翼，S.Kota等[5]在美国空军实验室提供的基金支持下，以NACA63418翼型为基础，结合柔性机构进行设计并制造出了可变弯度的前缘柔性结构。风洞试验结果显示，该柔性机翼在升力系数提高了25%的同时，升阻比提高了51%。S.Kota等[6]结合柔性机构，开发了几何可变的柔性前缘结构，其可变几何叶片能够使气动性能保持最优，从而延缓了叶片失速，在前进速度、承载能力以及机动性能方面均产生了明显的收益。H.P.Monner等[7]提出了智能无缝的前缘装置概念，该装置采用玻璃纤维，使用不同的铺层，使机翼前缘能够按设计刚度分布，同时沿展长方向布置一定数量的桁条来加强结构，从而较好地实现了变形能力和承载要求的平衡。N.D.Matteo等[8]采用曲线梁作为驱动单元，并使用铝作为蒙皮材料，并设计了8个I型的金属筋条加强结构。

关于自适应变弯度后缘机翼，H.P.Monner[9]提出了形似“手指”的变形概念，这种结构使机翼的弯度能够同时沿弦向和展向进行变化，从而实现了机翼的自适应扭转变形。L.F.Companile等[10]设计了一种“肋带”形状的可变弯度机翼，采用分布式的柔性结构来代替之前的铰链结构，使其具有大变形、高承载能力和小重量等特点。D.P.Wang等[11]利用偏心梁的变形原理进行了后缘控制表面的设计，该设计由10个独立的翼段共同组成，其中每个翼段分别与偏心梁进行集成，使其能够在0.2s内获得最大20°的偏转。D.S.Ramrakhyani等[12]采用腱结构来驱动由数个六节点的八面体单元集成的桁架，从而实现了超过椭圆机翼面积50～200%的展向弯曲变形。S.Barbarino等[13]设计了一种以SMA为基础的机翼变形后缘结构，该后缘结构由5块薄板组成，薄板依次相连，薄板间安装有交叉的弹性薄片。U.Icardi等[14]设计了依靠SMA驱动并采用柔性蒙皮的变体机翼，该机翼结构由夹心盒段、柔性翼肋和柔性蒙皮组成，能够实现整体机翼的弯曲和表面局部的变形。A.Wildschek等[15]设计了全部以复合材料为结构的变形后缘，该机翼由电机驱动内部结构，电机与杆铰接，后缘偏转的曲率可通过改变梁的刚度来调节。N.D.Matteo等[16]提出了应用在大飞机高升力翼型上的变形后缘襟翼方案，采用开放式的滑动后缘，通过调节曲线梁使其改变当前构型。T.A.Probst等[17]以MFC为驱动器，对展长为0.5m的无人机进行弯曲变形控制，分别通过闭环及开环反馈系统来控制位移。D.Kim等[18]设计了可控制的变形后缘，并采用FMC进行驱动，该设计通过将伸长的驱动器嵌入上蒙皮，收缩的驱动器与下蒙皮连接，从而使后缘端部产生向下的弯曲变形。

综上所述，目前机翼变弯度的方式通常只考虑到翼型的改变，没有考虑到变形结构的承载能力。另外，现有的柔顺机构方案大多关注后缘变形概念和功能实现，缺乏机翼安定结构与变形功能结构连接方式的考虑。结合各变形方案的优势和不足，本文选择柔性可变形功能翼肋作为变弯度机翼的驱动方式，考虑功能结构的承载能力，并对可变形翼肋结构进行分析和试验，从而实现自适应机翼后缘变弯度方案的优化设计、分析与功能验证。

2 柔性翼肋方案设计与变形原理

2.1 变形概念及原理

柔性翼肋是一种可实现主动变形的翼肋结构。本文采用的柔性翼肋变形方案基于前期拓扑优化方法进行拓扑结构设计，并经过参数优化和圆整实现。该后缘柔性翼肋变形方案主要结合了悬臂梁受剪时弯曲变形的原理，整个结构通过将翼肋上端固支，下端只放开一个方向的平动自由度的方式与外部进行连接。向下弯曲变形时，直线舵机对柔性翼肋中部结构的前端提供机翼剖面弦向指向前缘的驱动力，这个驱动力传导到翼肋拓扑结构连接点时，向上的两部分分别对柔性翼肋的上端结构产生向下的剪力，使其向下弯曲，而向下的部分对柔性翼肋的下端结构产生向上的剪力和向前缘方向的轴力，使其向上弯曲的同时向前缘方向滑动，从而使整个柔性翼肋产生向下弯曲的变形效果(如图1所示)。而柔性翼肋向上弯曲变形时，整个传力及变形过程则正好相反。

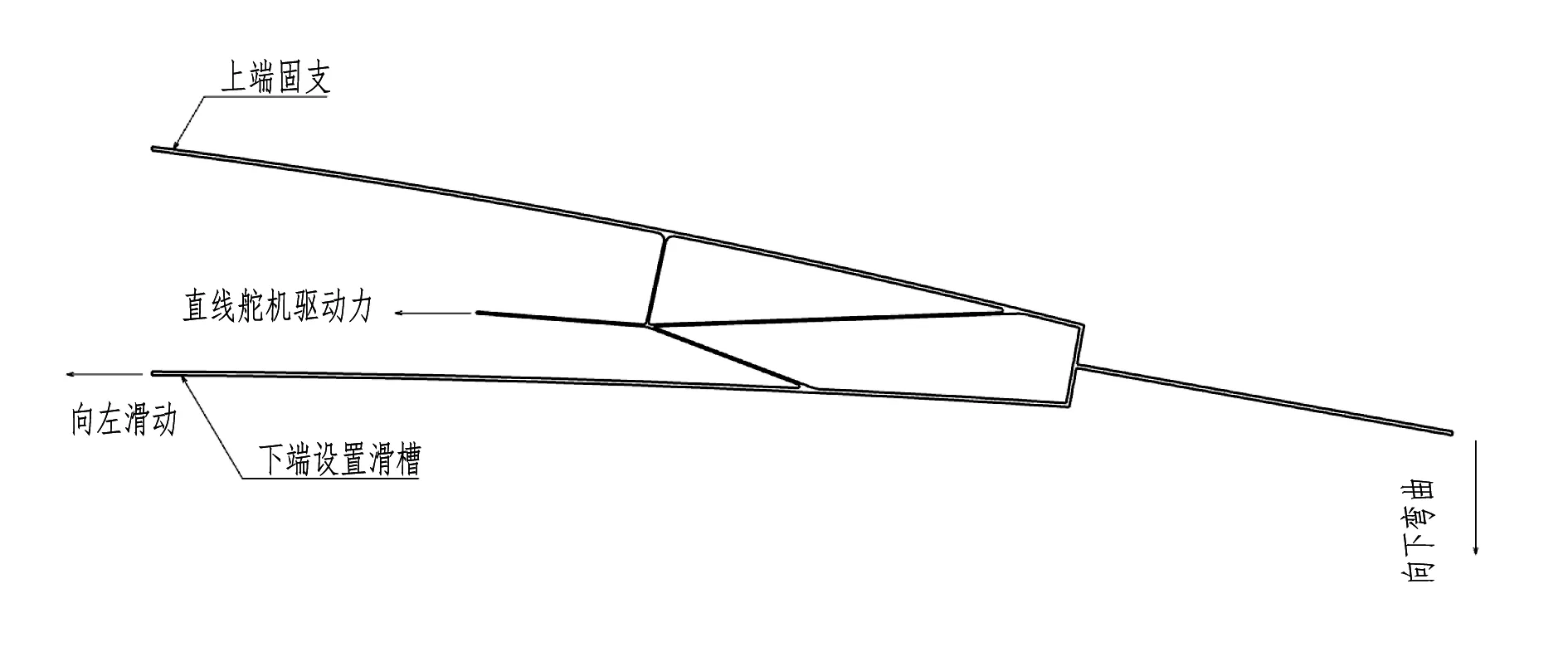
图1 后缘柔性翼肋变形原理

本方案后缘变弯度机翼设计采用NACA6409翼型，如图2所示。该翼型的相对弯度为6%，最大弯度位置在0.4弦长处，相对厚度为9%。

图2 NACA6409翼型

2.2 后缘柔性翼肋的模块化设计

模块化设计有设计通用、装配准确、更换便捷等优点，在柔性后缘的设计与试验过程中，通过模块化设计方法，可以在不改变外部连接结构的情况下，通过修改后缘柔性翼肋模块内的结构设计，使相同机翼结构匹配多种不同柔性翼肋结构，从而便于柔性翼肋结构的试验与设计优化。

模块化柔性后缘设计方案如图3所示，该方案将整体柔性后缘设计成一个模块单元，并通过连接支架与外部结构连接。另外，针对后期加工中可能出现的误差，柔性后缘模块的连接支架在与外部结构连接的部分分别设计了定位孔和定位槽。其中，定位孔分别与机翼后梁的上下缘条用螺栓连接来确定柔性后缘模块在机翼后梁上的具体位置，而另一侧的定位槽则可以让整个柔性后缘模块在10°的范围内进行转动，从而确定后缘柔性翼肋与后梁的准确夹角。在定位后，用紧固件产生的摩擦进行固定。

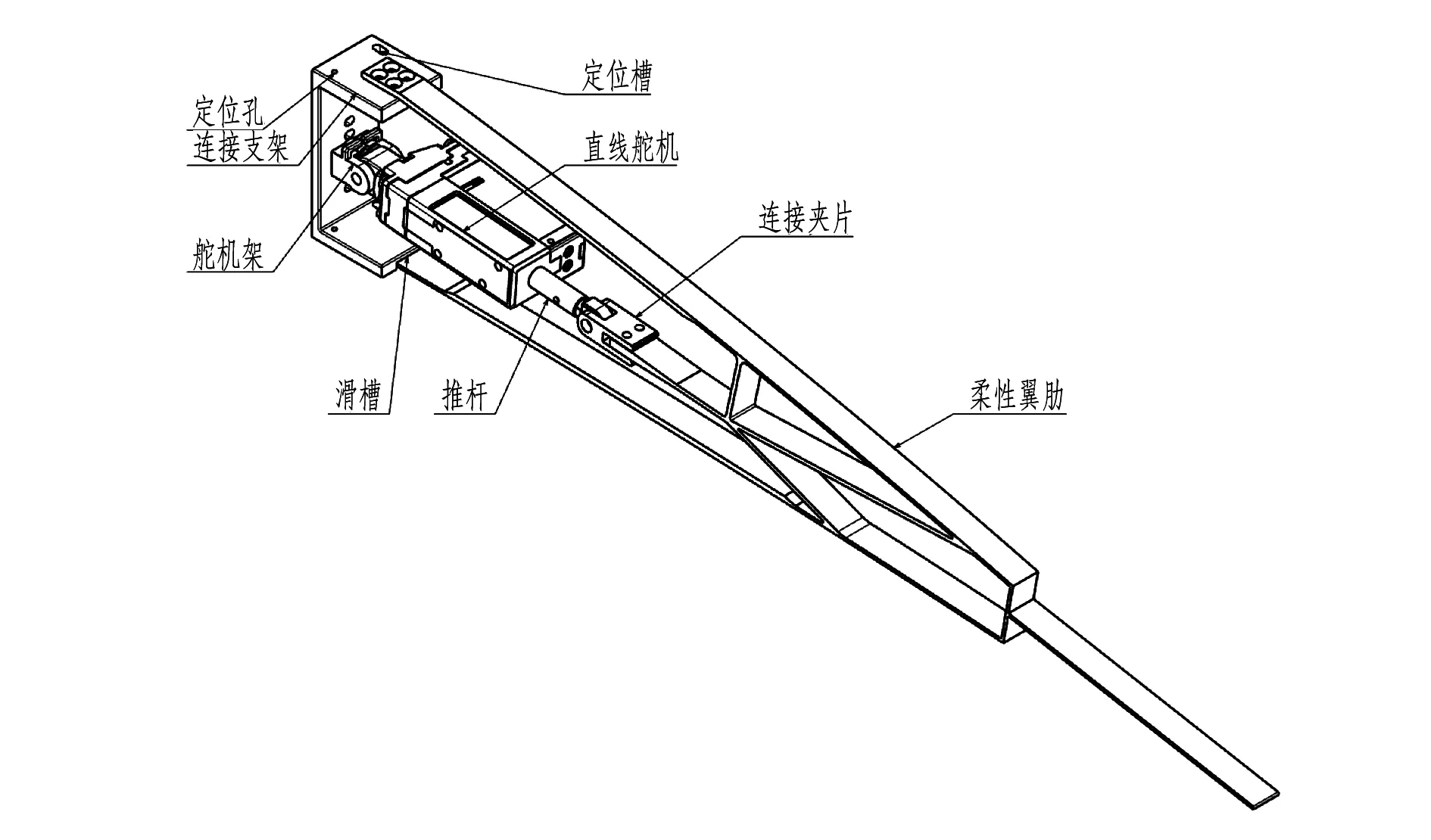
图3 模块化柔性后缘设计

此外，为了保证整个柔性后缘模块安装完成后，直线舵机的推杆产生的驱动力保持最高效的方向，在定位支架连接舵机架的部位分别设计了上下各两个孔位，左右各0.5mm的裕度，便于直线舵机的安装位置在水平和竖直方向留有一定裕度。另外还设计了特定尺寸的紧固件，用以将直线舵机固定在最佳位置上。

3 后缘柔性翼肋模块的建模、分析及参数优化

3.1 气动载荷计算

3.1.1 流场网格处理

根据初始的机翼翼型和平面尺寸，利用pointwise绘制如图4所示的机翼翼面网格。其中，前缘和后缘部分网格进行加密处理，并在翼面附近设置边界层网格。

图4 翼面气动网格

流场计算域选择长方体计算域，如图5所示。计算域左右边界距离机翼均为20倍翼根弦长，计算域上下边界距离机翼均为5倍翼根弦长，展向边界距离机翼12倍翼根弦长。整体流场计算域长20m，宽13m，高10m，网格数量110余万。右边界设置为对称面，前边界设置为速度入口，后边界设置为自由出口，翼面及流场其余部分均设置为物面。

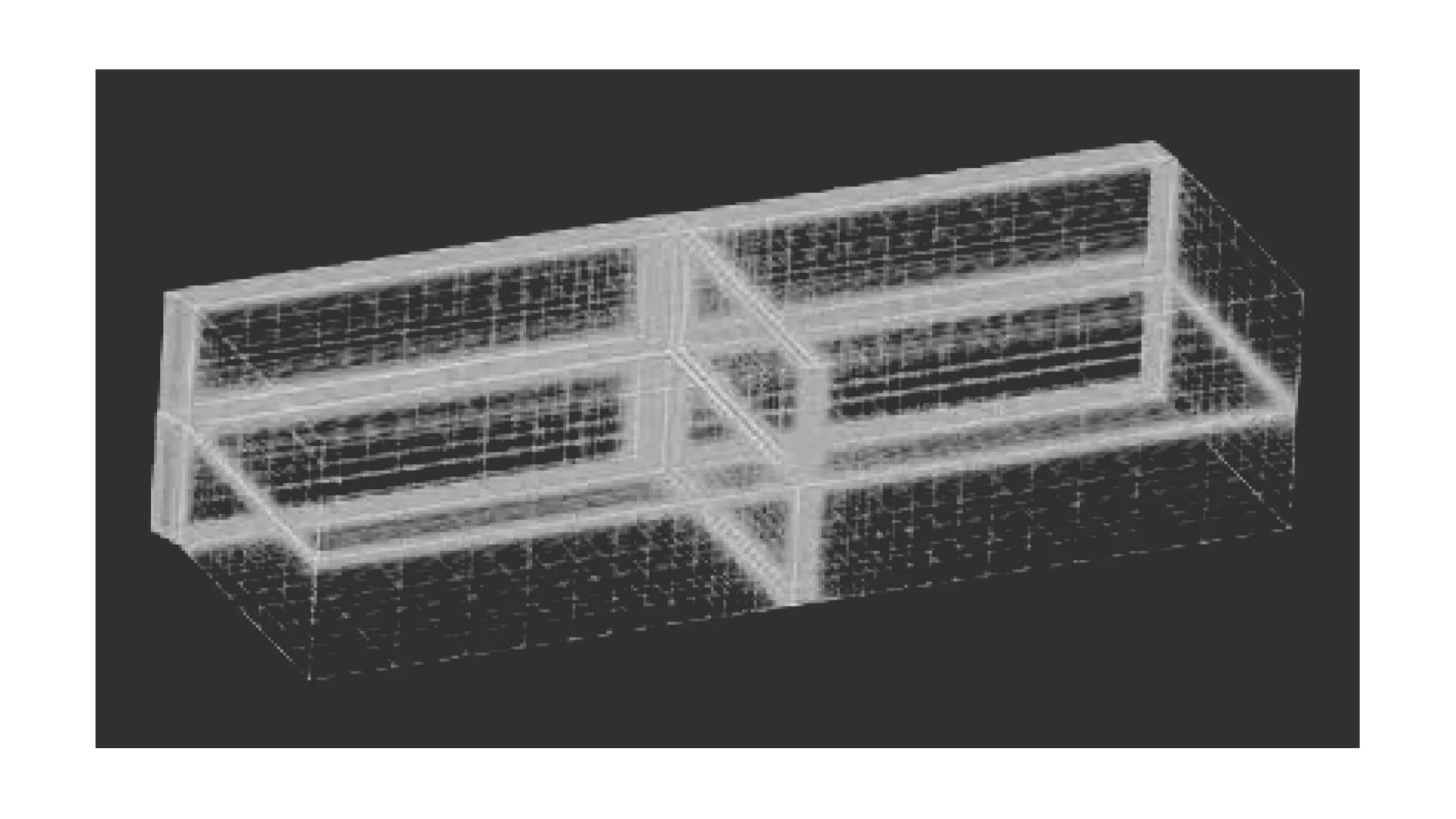
图5 流场气动网格

3.1.2 气动力计算

将绘制完成的机翼气动网格模型导入fluent对巡航状态下机翼的气动力大小及分布进行计算，具体计算条件如表1所示。

表1 巡航状态参数

按巡航状态参数进行计算，可得机翼升力系数为0.414，阻力系数为0.026，升阻比为15.9。由式(1)，可计算得到机翼整体的升力为219N。

(1)

式中，L为机翼升力；ρ为空气密度；v为来流速度；CL为升力系数；S为机翼面积。

计算完成后，利用fluent的后处理功能提取靠近翼根处的单个襟翼部分柔性翼肋和副翼部分柔性翼肋处的截面速度云图，如图6所示。从图中可以看出NACA6409翼型表面的速度随翼型弯度改变的分布情况，从而得出压强在机翼表面的大致分布趋势。

图6 柔性翼肋截面速度分布

另沿展向等距选取14个截面，提取每个截面上翼型表面各处的压力系数，利用matlab将数据进行整理，绘制出机翼表面压力系数分布图，如图7所示。

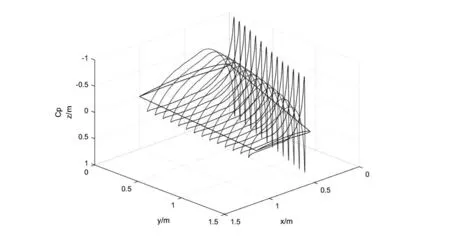
图7 机翼表面压力系数分布

分别提取靠近翼根处的单个襟翼部分柔性翼肋和副翼部分柔性翼肋截面的压力系数，并由公式(2)得出作用在柔性翼肋上的压强分布，如表2所示。

(2)

式中，Cp表示压力系数，p表示翼面压强，p∞表示来流压强，V∞表示来流速度。

表2 襟翼柔性翼肋压强分布

3.2 柔性翼肋结构建模、分析及参数优化

3.2.1 柔性翼肋结构有限元模型建立

根据柔性翼肋初始几何模型提取各个曲面，在patran中分别建立襟翼部分柔性翼肋和副翼部分柔性翼肋的结构有限元模型，如图8所示。各柔性翼肋的属性均设为2D板/壳单元，根据实际情况，将柔性翼肋的材料设置为钛合金，其弹性模量为110GPa，密度为4500kg/m3。

图8 柔性翼肋结构有限元模型

根据实际约束情况，分别将柔性翼肋上表面前端固支，下表面只放开弦向平动自由度。柔性翼肋加载工况主要分为驱动变形和受载变形两部分。其中，驱动变形工况在柔性翼肋中间部分施加x向驱动力，模拟直线舵机驱动力，从而计算柔性翼肋的整体变形情况及应力分布。受载变形工况时，将柔性翼肋中间部分固支，模拟直线舵机的锁死模式，同时将之前提取的气动载荷分别加载到柔性翼肋的上下表面，从而计算在气动载荷作用下柔性翼肋的变形情况、应力分布以及直线舵机锁死所需的驱动力大小。

3.2.2 柔性翼肋厚度优化设计

初始柔性翼肋模型外围各边厚度1mm，内部各边厚度0.5mm，加载气动力计算结果显示，柔性翼肋变形量较大，难以满足设计要求。

分别对后缘柔性翼肋的不同部分进行加厚处理，分组情况如表3所示。根据分组情况，在气动载荷作用工况下，分别对各组柔性翼肋结构有限元模型进行变形大小及分布情况计算。计算结果显示，翼肋外围靠近梁的部分加厚对一定驱动力下翼肋的最大变形起主要作用，翼肋内部的部分和下表面的部分加厚对一定载荷下翼肋的最大变形起主要影响作用。

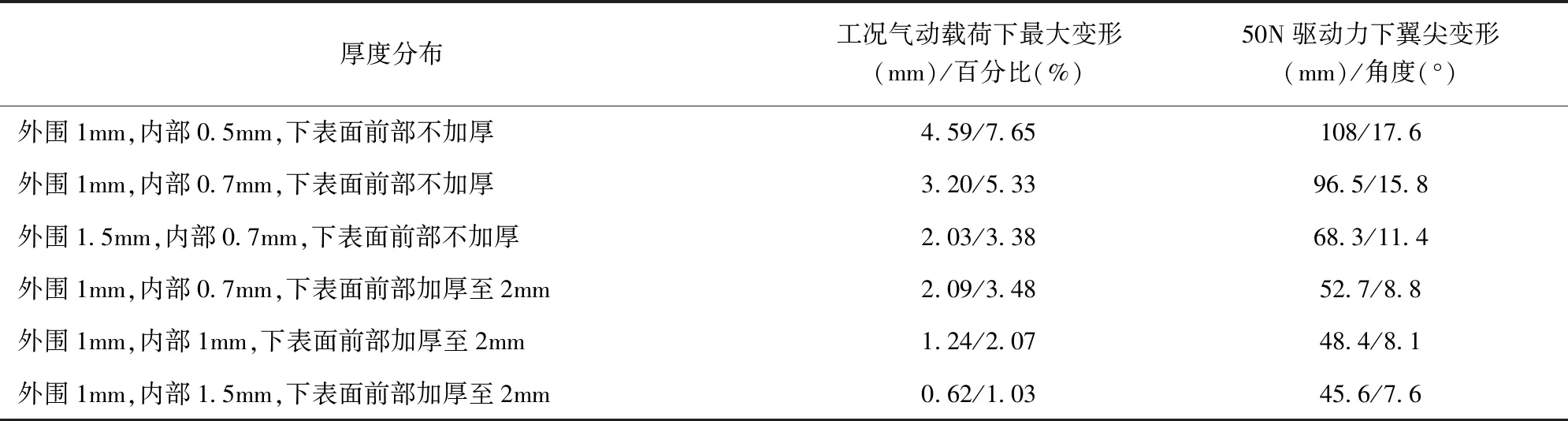
表3 厚度优化设计

以工况气动载荷下柔顺翼肋最大变形不超过1%为条件，50N驱动力下翼尖变形为目标进行厚度优化，柔性翼肋厚度优化结果如图9所示，具体为：柔性翼肋的上表面前端和下表面前端分别加厚至2mm，中间连接部分1.5mm厚，其余部分1mm厚。

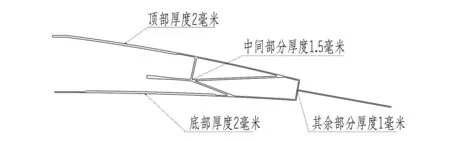
图9 柔性翼肋厚度优化设计

3.2.3 气动载荷下柔性翼肋静力分析

为了防止水稻在建设过程中出现塌陷，在隧道开掘中要及时做好支护工作，严格施工标准。CRD法大断面浅埋偏压隧道初期支护一般采用格栅钢架、钢筋网、φ22砂浆锚杆及湿喷混凝土，控制围岩变形。

将柔性翼肋的中间部分固支，并将之前计算得到的后缘气动载荷分别加在优化后的襟翼柔性翼肋和副翼柔性翼肋的结构有限元模型上，计算各柔性翼肋在气动载荷作用下的最大变形以及应力分布，结果如图10所示。

(a)变形分布

(b)应力分布图10 柔性翼肋气动载荷作用结果

由图10可知，在工况气动载荷作用下，柔性翼肋最大变形为0.632mm，出现在下表面靠近后缘的部分；柔性翼肋整体变形都在翼肋厚度的1%以下，对机翼的气动外形基本没有影响。最大应力为65.4MPa，出现在中间部分的固接处；整个柔性翼肋的应力均在钛合金屈服应力以下(取安全系数1.5，钛合金的强度极限为1000MPa)，整体强度和刚度均符合设计要求。

3.2.4 驱动力下柔性翼肋静力分析

按照实际约束状况，将柔性翼肋上表面前端固支，下表面仅放开弦向自由度，对柔性翼肋中间部分前端施加驱动力，分析自由状态下直线舵机驱动力与柔性翼肋尖端最大变形的关系，结果如表4所示。

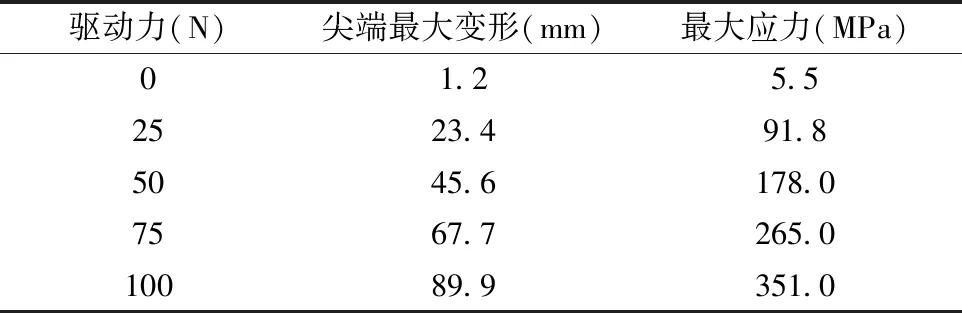
表4 不同驱动力下柔性翼肋变形及应力

分别对襟翼柔性翼肋和副翼柔性翼肋在自由状态不同大小驱动力作用下后缘尖端最大变形及最大应力数据绘制成散点图并进行关系拟合，结果如图11、图12所示。

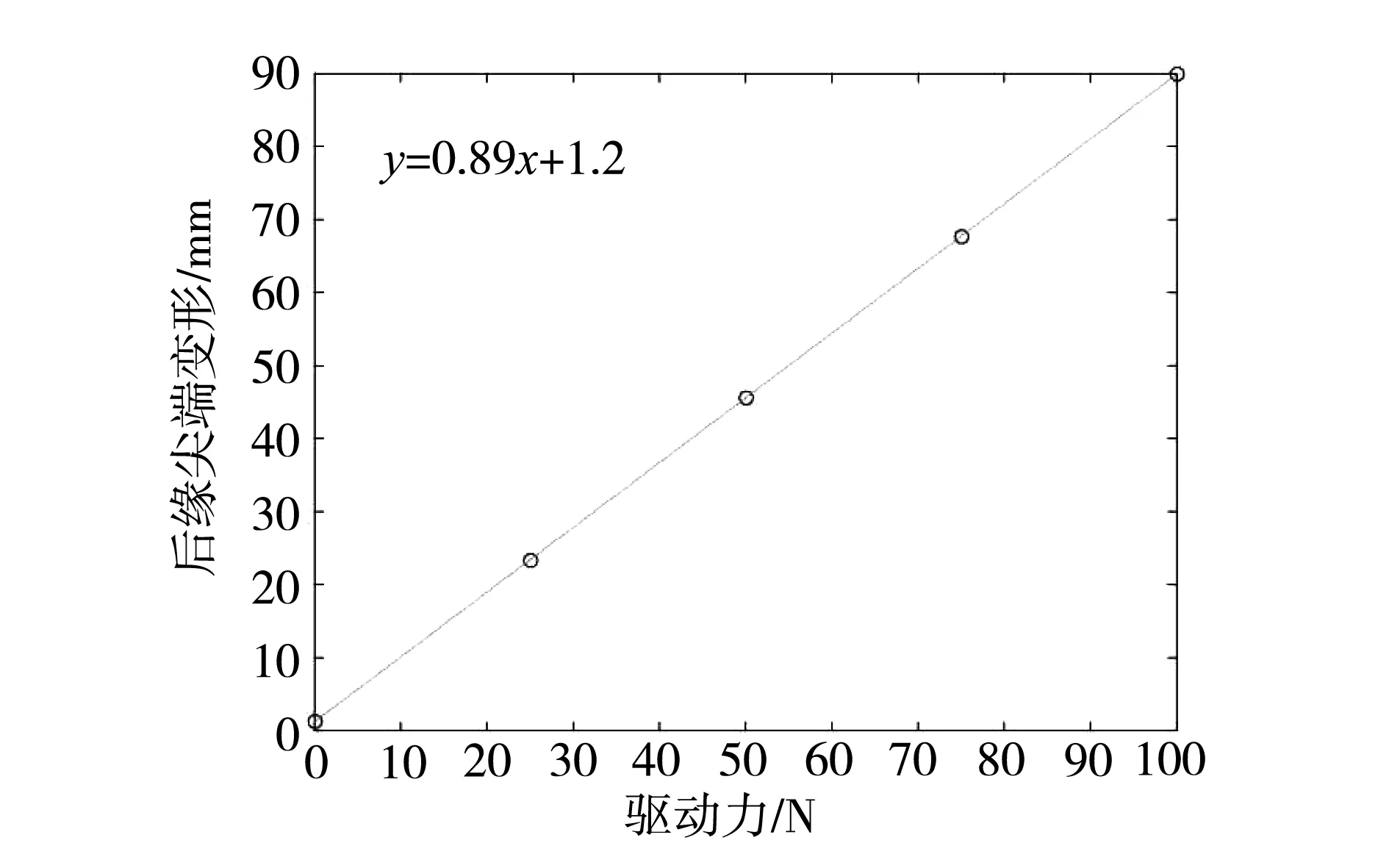
图11 后缘尖端变形随驱动力变化

由图11可知，柔性翼肋尖端最大变形量与驱动力变化呈线性关系，即柔性翼肋的驱动变形能力与最大驱动力线性相关，相关关系方程如图11所示。在100N的最大设计驱动力作用下，柔性翼肋的后缘尖端最大变形超过10°，满足自由状态下柔性翼肋变形能力的要求。

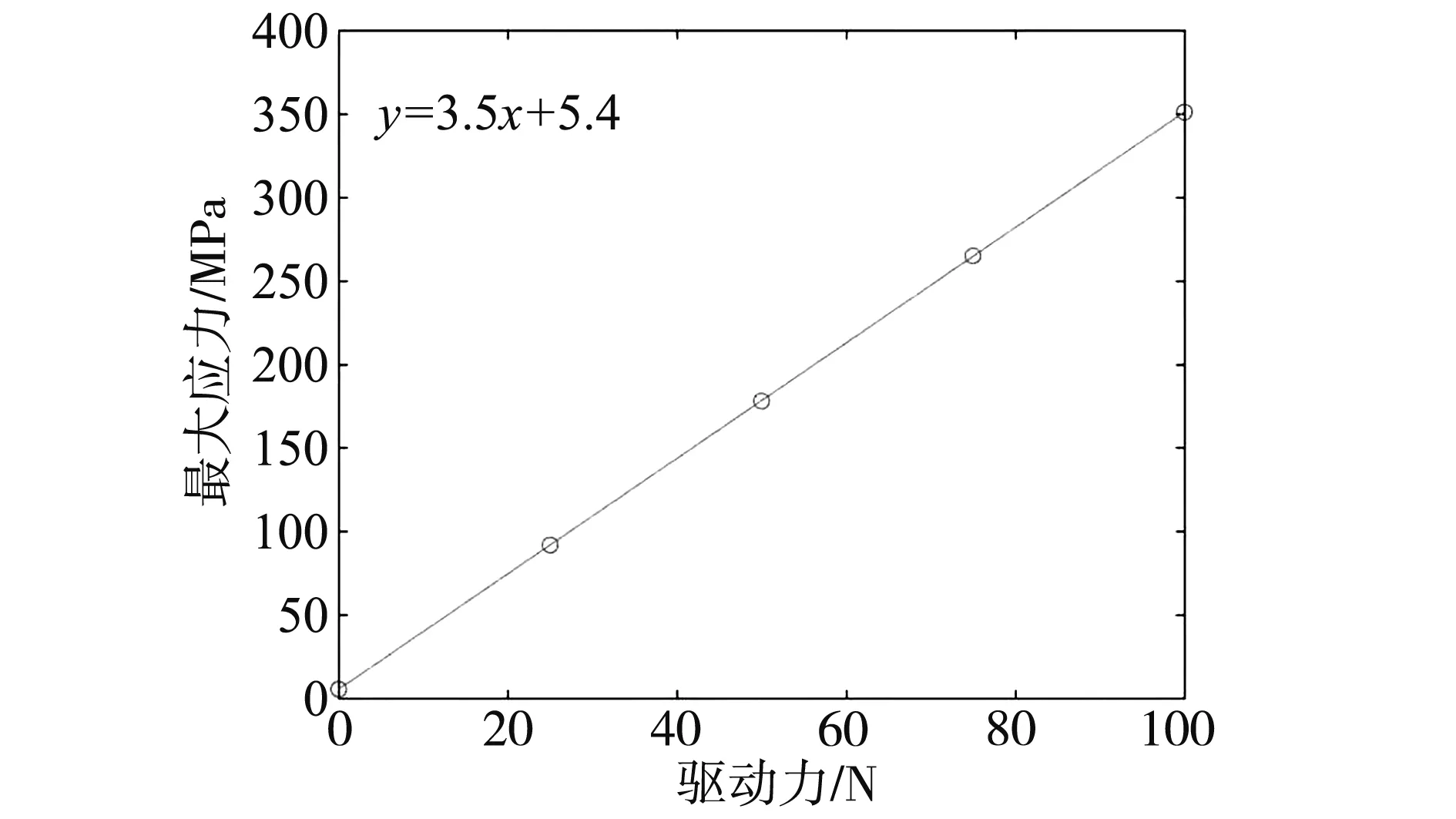
图12 柔性翼肋最大应力随驱动力变化

由图12可知，柔性翼肋最大应力与驱动力变化呈线性关系，即柔性翼肋中的最大应力与驱动力线性相关，相关关系方程如图12所示。在100N的最大设计驱动力作用下，柔性翼肋的最大应力未超过600MPa，小于钛合金的屈服应力，满足强度设计要求。

3.2.5 直线舵机驱动力估算

在保持实际约束条件的情况下，将之前计算得到的气动载荷加在柔性翼肋上，对柔性翼肋中间部分施加弦向驱动力，计算不同驱动力下柔性翼肋后缘尖端的变形情况，如图13所示。

图13 气动载荷下柔性翼肋尖端随驱动力变化

y=-0.89x+40

(3)

由式(3)可知，襟翼柔性翼肋在驱动力为45N时，后缘尖端变形量接近于0，此时柔性翼肋的变形最小，对机翼气动外形的影响最小。另外，由式(3)还可计算出当直线舵机驱动力达到100N时，襟翼柔性翼肋在气动载荷作用下后缘尖端变形达到了49mm，超过了变形能力的设计要求，达到了最初的设计标准。

根据柔性翼肋设计要求的±8°的偏转角度，由三角函数关系可知，柔性翼肋后缘尖端的变形范围需要达到±48mm。结合气动载荷作用下驱动力与后缘尖端变形的拟合方程，可以通过计算得到柔性翼肋所需的直线舵机的驱动力范围在9N到99N之间。再结合直线舵机5mm/s(后缘尖端每秒偏转7°)的驱动速度设计要求，可以通过计算得到所需直线舵机的最大驱动功率为0.5W。

为验证拟合结果，对气动载荷作用下的柔性翼肋在45N驱动力下的变形情况和应力分布情况进行计算，计算结果如图14所示。

(a)变形分布

(b)应力分布图14 柔性翼肋气动载荷与45N驱动力作用情况

由图14可知，在气动载荷和45N驱动力共同作用下，柔性翼肋后缘尖端最大变形为0.147mm，证明总体拟合情况良好，符合设计刚度要求。最大应力为68.2MPa，远小于钛合金的屈服应力，满足强度设计要求。

4 后缘柔性翼肋模块地面试验

4.1 试验系统

后缘柔性翼肋模块固定装置即后缘变弯度机翼地面模型如图15所示。根据后缘柔性翼肋模块弯曲变形试验所需的试验器材，搭建如图16所示的后缘柔性翼肋模块变形试验系统，其对应实物系统如图17所示。

图15 后缘变弯度机翼地面模型

图16 柔性翼肋模块变形试验系统连接关系

1.计算机 2.测量底板 3.柔性翼肋模块 4.稳压电源 5.USB-PC控制器图17 柔性翼肋模块变形试验系统实物

柔性翼肋模块通过USB-PC控制器分别与计算机和稳压电源连接。计算机控制直线舵机驱动软件，控制直线舵机的开关以及驱动步数；稳压电源提供直线舵机所需的7.4V电压。试验前首先将直线舵机的推杆调整至中立位置，即驱动步数为2048，之后将舵机推杆与柔性翼肋中部连接夹片进行安装，安装完成后即可通过增大或减少舵机的驱动步数来调整舵机推杆的目标位置，从而完成柔性翼肋的驱动变形。

4.2 空载与加载状态变形速率测试

首先，在空载状态下通过调节舵机驱动速率来测试后缘柔性翼肋的变形速率，柔性翼肋中立位和下偏位如图18所示。再对柔性翼肋进行加载，试验系统与加载方案如图19和图20所示。

图18 柔性翼肋中立位(左)和下偏位(右)

1.加载模块 2.后缘柔性翼肋图19 后缘柔性翼肋加载试验系统

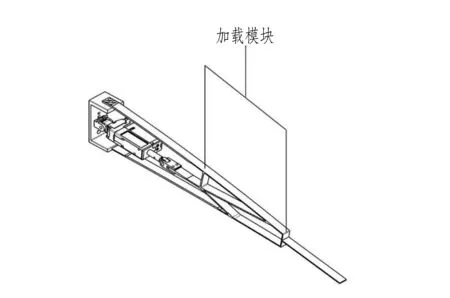
图20 柔性翼肋加载方案

沿弦长方向设置2个加载点，单个后缘柔性翼肋设置加载2kg，均匀分布在2个加载点上；各个加载点方向均竖直向上。使用与空载状态下相同的方法对加载状态的柔性翼肋进行变形速率测试，结果如表5所示。

表5 测试结果

4.3 柔性翼肋后缘尖端变形与驱动位移关系

将襟副翼柔性翼肋模块的后梁连接部分固定，之后分别对襟翼柔性翼肋模块和副翼柔性翼肋模块在设计变形范围内给定一系列直线舵机驱动位移，测量襟翼柔性翼肋和副翼柔性翼肋的后缘尖端在竖直方向的变形量，具体结果如表6所示。

表6 柔性翼肋尖端变形与驱动位移关系

为便于观察直线舵机驱动位移与柔性翼肋尖端变形之间的关系，将表中数据绘制成散点图，如图21所示。

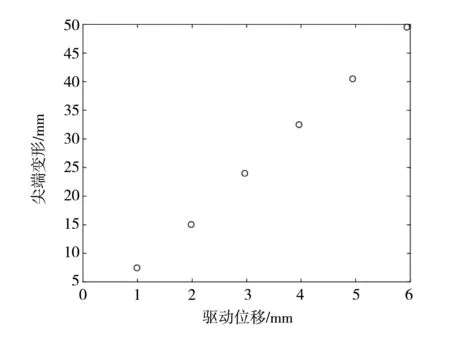
图21 柔性翼肋尖端变形与驱动位移关系

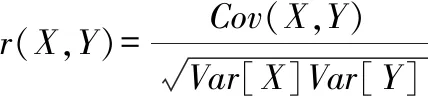
(4)

由式(4)计算可知，襟翼柔性翼肋后缘尖端变形量与直线舵机的驱动位移之间的线性相关系数为0.9998，副翼柔性翼肋后缘尖端变形量与直线舵机的驱动位移之间的线性相关系数0.9923。由计算结果可知，襟翼柔性翼肋和副翼柔性翼肋的后缘尖端变形量与直线舵机的驱动位移量呈强线性相关关系，且两者的相关关系为正相关。

4.4 试验数据与计算结果对比分析

利用襟副翼后缘柔性翼肋模型，在施加实际约束的条件下，分别对柔性翼肋中间部分施加不同的弦向位移驱动，计算出襟翼柔性翼肋和副翼柔性翼肋的后缘尖端变形，计算结果见表7。

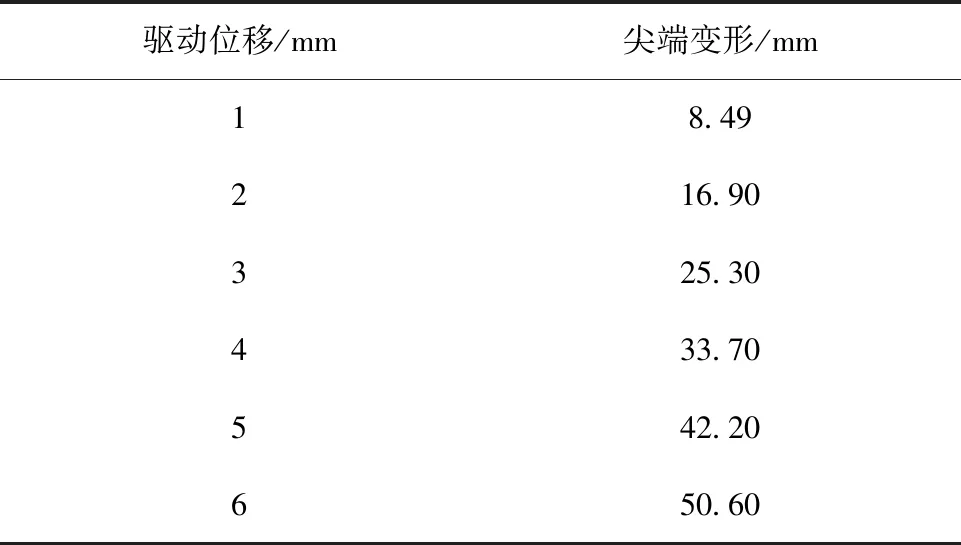
表7 柔性翼肋驱动位移与尖端变形计算结果

将柔性翼肋的计算结果绘制成图并进行线性关系拟合，并将之前测得的试验数据以散点的形式绘制在图上，结果如图22所示。

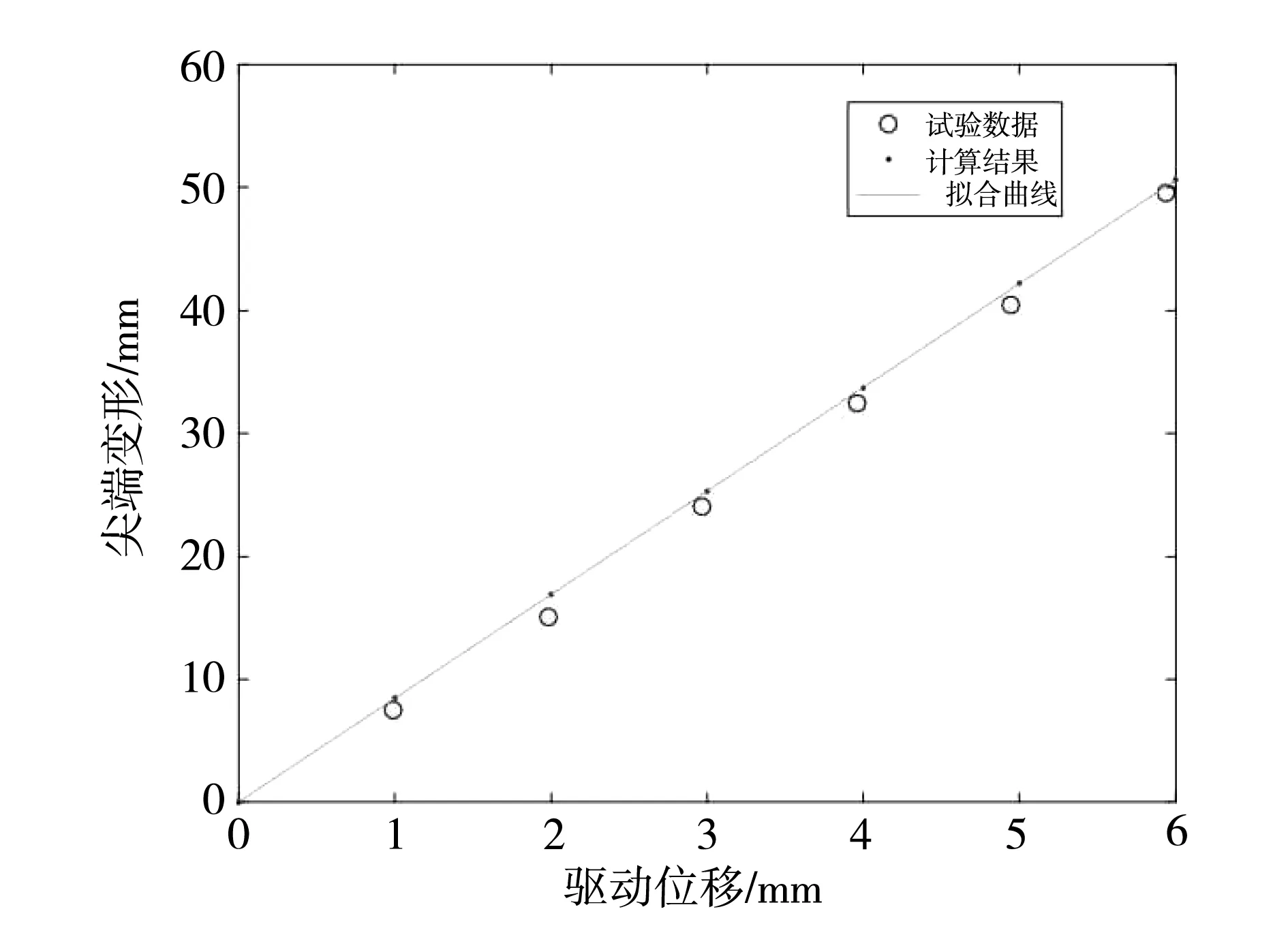
图22 计算结果与试验数据对比

根据试验数据与计算结果的对比可知，柔性翼肋后缘尖端与直线舵机驱动位移之间呈线性相关关系，且试验数据与计算结果的曲线趋势基本相同，两者符合关系较好。

5 结 论

(1)基于本文柔性翼肋变形方案制作的后缘变弯度机翼地面模型可以实现后缘翼肋剖面的光滑、连续变形，变形品质良好，柔性翼肋模块变形能力达到±15°。

(2)结构有限元模型分析结果表明，该方案的设计功率及驱动力需求小于现有直线舵机的驱动功率和驱动力，满足驱动要求。整体机翼和优化后的柔性翼肋设计方案满足工况气动载荷下的强度和刚度要求，设计方案合理可行。

(3)开展了柔性翼肋模块自由状态与加载状态下的变形试验，地面试验测试结果表明，后缘柔性翼肋受载状态下实际变形能力仍超出±15°范围；直线舵机驱动位移与后缘尖端变形符合线性相关关系，并与有限元分析结果相同。