基于改进灰度算法的分数预测模型应用
王舒 李浩* 钟科 聂珊 周文安
(1.四川省计算机研究院 四川省成都市 610041 2.四川大学招生办公室 四川省成都市 610065)
在我国,高考一直是一个重要事件,它对于考生以及考生家庭都有着重要的意义,它关系着考生大学四年的学习以及未来人生发展,被很多人视为人生的一次转折。这些年我国的高考志愿填报方式逐渐改革,由之前的考前填报、估分填报变为了考后拿到成绩再填报,这种填报方式降低了考生因发挥异常而与填报学校失之交臂的风险,但同时,如何根据自己的成绩填报理想的志愿尤为重要[1]。
高考志愿填报辅助系统目前有两类,一类是通过考生的心理测评来为考生推荐适合考生的专业和院校[2];另一类是以历史高考成绩为依据,为考生推荐符合成绩范围的专业和院校[3,4]。这一类高考志愿填报系统目前国内有一些,提供往年高校录取分数、比例介绍,专业简介和就业前景等信息描述。总体来说推荐的信息量较大,但是大多数是信息的罗列而缺少对信息底层数据的挖掘与分析,重点推荐,因此并不能解决考生志愿填报的盲目性。
本文围绕上述内容展开研究,通过对分数标准化方法的改进并结合灰度预测模型,设计并实现了基于改进灰度算法的分数预测模型,并应用于高考志愿决策系统,能够快速和准确地给出高校录取分数的预测结果。
1 相关工作
本文的研究工作主要以标准分转换为基础,并应用了灰度预测模型,因此对标准分计算、灰度预测模型进行了相关研究。
1.1 标准分计算
标准分制度是根据教育测量学理论建立的一套有关分数报告、分数解释和分数使用的制度。它向考生报告各科标准分及百分等级,报告总分(改称综合分)的标准分百分等级[4]。其标准化过程如下:
设构成原始成绩的集合为{x1, x2,x3, …, xn},则平均分计算公式为:


表1:标准分转换结果
标准差为:

对于任意原始分xi有:

则称Zi是xi的标准分,也称Z 分数。
目前我国高考标准分[6]采用CEEB 分数,计算方法为:

采用标准分比采用原始分计算优点是十分明显的,因为标准分主要体现的是考生的排名情况,但是针对本系统来说,传统的标准分计算方法存在以下不足:首先标准分是按照正态分布来计算的,但是由于每年的考生水平以及考题难易程度不相同,考生成绩分布情况受影响;其次如果数据不完整会导致计算结果不准确。因此有研究者提出使用位次信息作为分析依据,但是考生动辄数万名,为此信息在计算以及表示的时候都不够直观,文献[6]提出,通过一分一段将分数转换为位次,再由位次转换为分数,这样做可以解决上述问题。但是却忽略了一个问题,即在分数与位次转换过程中,一个位次对应的分数是唯一的,而一个分数对应的位次不唯一。以四川省高考数据为例,2019 年理科分数为655 的共有300 名考生,排名6671 至6971,因此这个排名段内的名次均对应了理科655 分。
基于上述问题本文提出了一种新的标准分计算方法,能够更准确地将分数与位次的对应关系表示出来。
1.2 灰度预测
定量预测方法有很多,目前应用比较广泛的有神经网络法、回归分析法、时间序列法、灰色预测法等等[12],这些方法各有优缺点。而针对高考数据分析来说,首先样本不需要过多,因为随着区域以及高等教育的发展,多年以前的高考数据基本不具有参考性;其次高考分数分布没有明显的规律。因此灰度预测法适用于分数线的预测。
灰度预测是由邓聚龙教授在上世纪八十年代提出的[7]。它具有如下几个特点[8]:
(1)不需要大量样本;
(2)样本不需要有规律性分布;
(3)计算工作量小;
(4)定量分析与定性分析结果不会不一致;
(5)可用于Recent、短期、中长期预测;
(6)灰度预测准确率高。
文献[9~10]以及文献[13]采用了灰度预测模型对高考录取分数进行了预测,文献[14~16]针对灰度预测模型本身进行了改进研究。但目前的研究中并未将高校录取人数变化对高校录取分数线的影响引入到灰度模型中做改进测试。

图1:标准分与原始分对比

图2:算法结果对比
一所高校招生人数增多或者减少都会影响考生对该校志愿的填报意愿,从而影响该校录取分数线。基于上述研究本文对灰度模型计算方法加以改进,引入了影响因子,更满足高校分数预测的实际需求。
2 改进标准分计算
改进标准分计算方法如下:{s1, s2, …, sn}表示n 所高校在最近一年录取分数线,根据一分一段得到排名为{r1, r2, …, rn},其中r={Rlow, Rhigh},表示最低排名到最高排名区间范围。根据r 转换为该高校历年分数{Sy1, Sy2, …, Sym},SS={Wlow, Whigh}即为某高校在某年度的标准分。
以五所高校(中国人民大学RUC、南开大学NKU、吉林大学JLU、江苏大学JSU、东北林业大学NEFU)在四川省内2015 年~2018 年的高考分数为例,基于2019 年的标准分转换结果如表1所示。
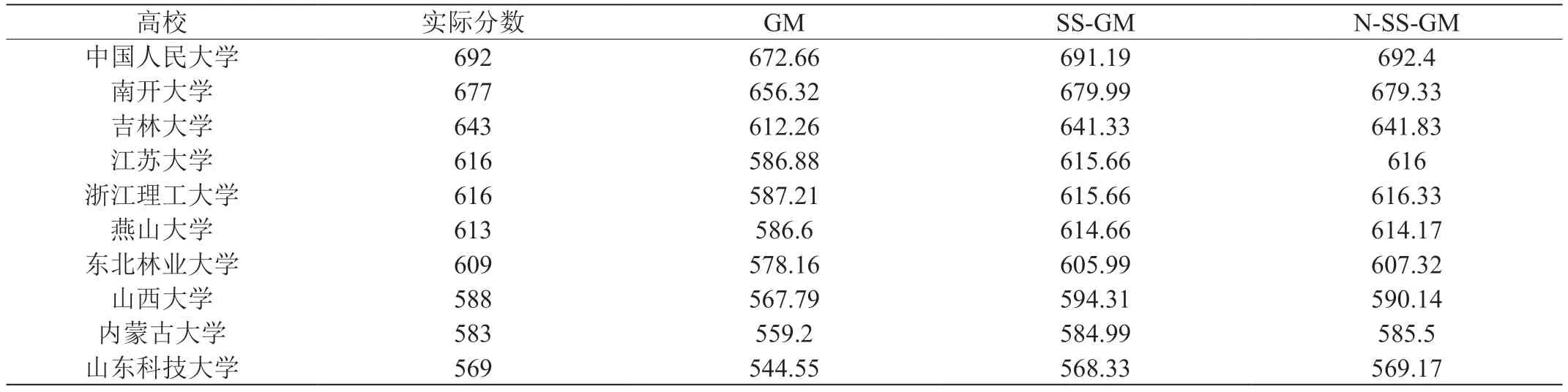
表2:实验结果

表3:误差比对
观察表1 可以看出,高校原始录取分数分差较大,没有直观的可比性,通过转换为标准分后,分数比较平缓,说明该学校在四川省内收分处于一个较稳定的区间内,更利于学生参考。从上表中选取吉林大学,将转换前与转换后的分数进行对比如图1 所示。
根据图1 可以看出转换后的数据相比之前的数据,提高了数据一致性,解决了因分数波动对分数预测造成的影响。
3 改进灰度算法的分数预测模型
设某高校录取标准分原始序列为:
y(0)=(y(0)(1), y(0)(2), …, y(0)(n) ),d 为作用于y 的算子,它的定义为:

s0为该高校拟招生人数,S0为有效考生总人数,sn为该高校对应年的招生人数Sn为对应年有效考生总人数。则新序列为x(0)=(x(0)(1), x(0)(2), …, x(0)(n)),其中

计算该数列的级比为:

计算步骤如下:
(1)原始数据累加以便弱化随机序列的波动性和随机性,分别得到x^((0) )的一次累加生成数列

(2)对x(1)(t)建立x(1)(t)的一阶线性微分方程:

(3)对累加生成数据x(1)做均值生成B 与向量Yn,即

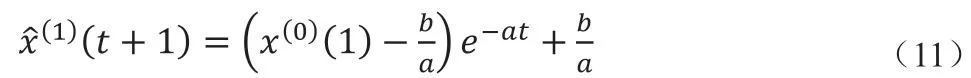

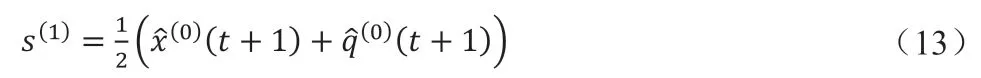
4 实验结果
分别对高校的录取分数采取原始分灰度预测(GM)、标准分灰度预测(SS-GM)、改进标准分灰度预测(N-SS-GM),抽取十所高校预测结果如表2 所示。
通过实验结果比对,不采用标准分预测的分数结果与实际分数相差较多,采用标准分预测和采用改进灰度预测模型预测结果更接近于实际分数。
通过对模型生成结果s(1)与真实数据s(0)之间的残差e 和相对误差q(x):

来验证文本算法的有效性,对上述10 个高校的计算结果进行检验,如表3 所示。
将计算结果用折线图表示,如图2 所示。
由图2 可以看出,改进的标准分灰度预测模型(N-SS-GM)的相对误差在大多数高校预测中要优于标准分灰度预测模型,山西大学由于在2019 年招生人数增加很大,所以改进后模型的误差率较低,而原始预测模型则误差率相对较高。总体分析改进后的算法误差率在很低的范围内,优于其他算法。
5 结束语
本文针对高考真实数据进行分析,采用了改进的标准分算法对标准分进行更直观化的转换,后采用改进灰度预测算法预测分数,实验结果证明效果很好。接下来的工作主要有以下几个方面:首先,扩大实验数据的范围,将方法应用于较低分数段进行验证;其次,在分析预测高校分数的基础上,预测专业的录取分数;最后将预测分数结果与录取率计算相结合,给出完整的报考指南。

