Counterexample of Local Fractional Order Chain Rule and Modified Definition of Local Fractional Order

FANKai(范凯)1，2，3，4，ZHOUCunlong1，2，3

1 Engineering Research Center of Heavy Machinery Ministry of Education， Taiyuan University of Science and Technology，Taiyuan 030024， China 2 School of Mechanical Engineering， Taiyuan University of Science and Technology，Taiyuan 030024， China 3 Shanxi Provincial Key Laboratory of Metallurgical Device Design Theory and Technology， Taiyuan University of Science and Technology，Taiyuan 030024， China 4 School of Applied Science， Taiyuan University of Science and Technology， Taiyuan 030024， China

Abstract: Fractional calculus is a powerful tool for modeling nonlinear systems. It is necessary to discuss the basic properties of fractional order before solving a fractional order model. Using the formula of power function defined by local fractional derivative and the chain rule to calculate a compound function， the results are inconsistent. This shows that the chain rule of local fractional derivatives similar to classical calculus is suspicious， and fractional complex transformation based on the chain rule is also suspicious and needs further discussion. In order to overcome this inconsistency， an improved definition of local fractional derivative， which can be regarded as a fractal derivative， is proposed based on the results derived from the relationship between the mass function and the Hausdorff measure.

Key words: local fractional order； chain rule； fractional complex transformation； fractal derivative

Introduction

Nonlocality and heritability are the salient features of fractional derivatives of Riemann-Liouville， Caputo， based on the definition of fractional integrals[1]. However， when we compare them to classical calculus， there are many inconsistencies， such as the multiplication and division rules that do not satisfy the derivatives of two functions and the chain rule.These inconsistencies bring great inconvenience to mathematical processing. In order to overcome these shortcomings， some scholars have proposed the concept of local fractional order. We list three definitions related to the discussion in this paper.In 2003， Parvate and Gangal[2]gave a fractal derivative from the fractal subset of solid lines. In 2006， Jumarie[3]obtained a modified Riemann-Liouville derivative through the difference scheme of Riemann-Liouville derivative. In 2012， Yang[4]introduced the theory of local fractional derivative and calculus，which can be viewed as the logical extensions of the definitions to the subject of local derivative on fractals.Under certain conditions， the fractional order definition of Yang is the same as that of Parvate and Gangal[2]. Li and He[5-6]first proposed fractional complex transformation for the modified Rieman-Liouville fractional order by Jumarie， which has been widely used since it was proposed. But in 2012， Heetal.[7]gave a counterexample to show that Jumarie’s modified Rieman-Liouville fractional order， like the chain rule of classical calculus， failed. Liu[8]demonstrated in 2015 that Jumarie’s Chain rule is not valid for differentiable functions through counterexample. And Liu[9]demonstrated in 2018 that Jumarie’s Chain rule is not valid for non-differentiable continuous functions through counterexample. Tarasov[10]even argued that the modified Rieman-Liouville fractional derivatives by Jumarie cannot be regarded as a fractional derivative through discussion of the fractional chain rule.The fractional complex transformation is derived based on the correctness of the chain rule. Therefore， the fractional complex transformation proposed by Jumarie to the modified Rieman-Liouville fractional order definition is questioned[11-12]. Then according to the definition of local fractional derivative， a new fractional complex transformation is proposed and widely used[13-17].Before solving the fractional-order derivative model， it is necessary to discuss some of its basic properties.

In this paper， a counterexample is given to illustrate the fractional complex transformation of local fractionalorder based on the chain rule， which needs further discussion.According to the relationship between the fractal derivative proposed by Parvate and Gangal[2]and the local fractional derivative introduced by Yang[4]， a modified local fractional derivative was proposed in order to overcome this counterexample and eliminate the doubts about complex transformation.

1 Counterexample of the Chain Rule of

LocalFractionalOrder

The definition of local fractional derivative in Ref. [18] is introduced. The local fractional derivative off(x) atx0is described as

(1)

where Δα(f(x)-f(x0))≅Γ(1+α)Δ(f(x)-f(x0)).

The derivative has the following rules[18]

(2)

Ify(x)=(f∘u)(x)， whereu(x)=g(x)， then we can get the following formula[18]

(3)

where the formulasf(α)(g(x)) andg(1)(x) are required to exist.

Ify(x)=(f∘u)(x)， whereu(x)=g(x)， then we can get the following formula[18]

(4)

where the formulasf(1)(g(x)) andg(α)(x) are required to exist. Equation (4) is also applied in Ref. [19].

Let us consider a compound function of the following form

y(x)=(f∘u)(x)，f(u)=u2，u(x)=xα.

(5)

Clearly， there are

y(x)=f(u(x))=x2α.

(6)

Apply Eq. (2) to Eq. (6) and get

(7)

Using the chain rule Eq. (4) to calculate Eq. (5)， the following result is obtained.

(8)

Because of the uncertainty ofα， Eqs. (7) and (8) are obviously different.That is to say， the chain rule Eq. (4) defined by local fractional order in this paper is not necessarily true.

2 Fractional Complex Transformation

BasedonLocalFractionalOrder

ChainRule

We first give the fractional complex transformation of local fractional order[13-14]， and the calculation details show that the fractional complex transformation based on local fractional order is also questionable.

Fractional complex transformation of local fractional order is

(9)

Through Eq. (9)， the following equation transformation exists

(10)

(11)

It can be seen from Eq. (11) that the key to the establishment of Eq. (10) lies in the establishment of the chain rule of Eq. (4). Therefore， the correctness of Eq. (10) is questionable.

3 Modified Local Fractional Derivative

Definition

In order not to repeat the contents of others’ articles， several concepts and results closely related to the definition of local fractional order are given here[2-4].

Equation (13) in Ref. [4] is

(12)

whereγα[F，a，b] is the mass function defined in Refs. [2， 4] andHα[F∩(a，b)] is Hausdorff measure. The calculation of Hausdorff measure can also be referred to the calculation of total variation similar to the Lebesgue measure[20]. In the first chapter of Ref. [21]，Hα[F∩(a，b)]=(b-a)αis also mentioned.

Equation (7) in Ref. [4] and Eq. (10) in Ref. [2] both define the integral staircase function as

(13)

wherea0is a fixed real number that can be arbitrarily selected according to needs. An important attribute of the integral staircase is emphasized as follows (see Ref. [2] for details).

(14)

Ifa0is equal to 0 in Eq. (13)， the following derivation is as follows (there are some derivations in Ref. [11]， but not all of them).

(15)

(16)

To better understand the limit sign in the derivative， consider thatx，y>0 are very close， or close to the minimum scale of the fractal， and Eq. (16) minus Eq. (15) is

Finally, as senior year began to wind down, I got a part-time job working at the local coffee shop. I had figured that the job would be easy and, for the most part, stress-free. I pictured myself pouring the best gourmet3 coffees, making delicious doughnuts, and becoming close friends with the regular customers.

(17)

Equation (17) is considered to be valid in fractal set theory[4]and is directly used as a conclusion in Ref. [4]. From this， we want to replace (y-x)αin the local fractional derivative withyα-xα， to get the definition of the fractional derivative of the functionf(x)at the pointxofα(0<α≤1).

(18)

Here the gamma function Γ(1+α) associated with dimensionαis special， and its appearance in the definition of derivative can be seen in Ref. [2]， as well as in the fractional derivative based on the generalized difference definition[22-23]. The definition expressed in Eq. (18) can be seen as a fractal derivative[24].

4 Chain Rule Discussion of Modified

LocalFractionalDerivative

If the first derivative off(x)exists， Eq. (18) has the following chain rule and is true for our counterexample.

(19)

The existence ofg(α)(x) means thatg(x) is continuous.

(20)

Using the limit proof chain rule，

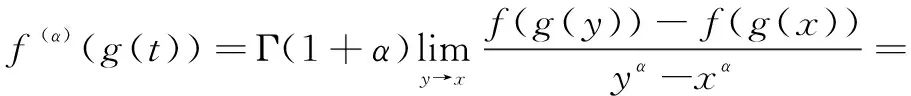
f(1)(g(x))g(α)(x).

(21)

For the counterexample mentioned in Eq. (5)， we use Eq. (19) to recalculate and get the following results

(22)

Directly use Eq. (18) to calculatey(x)=f(u(x))=x2α， and get

(23)

Equation (22) and Eq. (23) have the same result， indicating that the modified local fractional derivative definition overcomes the defect of the counterexample.In view of the fact that many chain rules of fractional derivatives are not valid， some scholars have proposed two-scale dimension and two-scale transformation as approximate applications[25-26]. The two-scale transform convert approximately a fractal space to a continuous partner[26].

5 Conclusions

Through the counterexample in this paper， we can see that the chain rule and definition of local fractional order derivatives are worth further discussion， and the fractional complex transformation based on the chain method of local fractional order derivatives naturally needs further discussion.In order to overcome this counterexample， a modified scheme of the local fractional derivative is proposed， which can be regarded as a fractal derivative.