Deep Knowledge Tracing Embedding Neural Network for Individualized Learning
HUANGYongfeng,SHIJie(施杰)
College of Computer Science and Technology, Donghua University, Shanghai 201620, China
Abstract: Knowledge tracing is the key component in online individualized learning, which is capable of assessing the users’ mastery of skills and predicting the probability that the users can solve specific problems. Available knowledge tracing models have the problem that the assessments are not directly used in the predictions. To make full use of the assessments during predictions, a novel model, named deep knowledge tracing embedding neural network (DKTENN), is proposed in this work. DKTENN is a synthesis of deep knowledge tracing (DKT) and knowledge graph embedding (KGE). DKT utilizes sophisticated long short-term memory (LSTM) to assess the users and track the mastery of skills according to the users’ interaction sequences with skill-level tags, and KGE is applied to predict the probability on the basis of both the embedded problems and DKT’s assessments. DKTENN outperforms performance factors analysis and the other knowledge tracing models based on deep learning in the experiments.
Key words: knowledge tracing; knowledge graph embedding (KGE); deep neural network; user assessment; personalized prediction
Introduction
Nowadays, programming contests are thriving, which involve an increasing number of skills and become dramatically difficult. But, available online learning platforms lack the ability to present suitable exercises for practicing.
Knowledge tracing is a key component to individualized learning, owing to its ability to assess the mastery of skills for each user and predict the probability that a user can correctly solve a specific problem. Introducing knowledge tracing into the learning of skills in programming contest can benefit both the teachers and the students.
Nevertheless, there are some challenges. The traditional knowledge tracing models, such as Bayesian knowledge tracing (BKT)[1](and its variants with additional individualized parameters[2-3], problem difficulty parameters[4]and the forget parameter[5]), learning factors analysis (LFA)[6]and performance factors analysis (PFA)[7], have the following two assumptions for the skills. First, the skills are properly partitioned into ideal and hierarchical structure,i.e., if all the prerequisites are mastered, one skill can be mastered after repeated practicing. Second, the skills are independent of each other,i.e., ifpAis the probability that a user correctly solves a problem requiring skill A, andpBis the probability that the user can solve another problem requiring a different skill B, it is assumed the probability that the user correctly solves a problem requiring both skills A and B ispA×pB, implying that the interconnections between skills are ignored. However, in individualized learning, a reasonable partition should make it easier for the users to master the skills instead of purely enhancing models’ performance. In addition, according to the second assumption, ifpA=pB= 1, thenpA×pB= 1. This is not in line with the cognitive process, since a problem requiring two skills is sure to be far more difficult than problems each requiring only one skill.
Recently, knowledge tracing models based on deep learning have been attracting tremendous research interests. Deep knowledge tracing (DKT)[8-11], which utilizes recurrent neural network (RNN) or long short-term memory (LSTM)[12], is robust[5]and has the power to infer the users’ mastery of one skill from another[13]. Along with its variants[14-15], like deep item response theory (Deep-IRT)[14], dynamic key-value memory network (DKVMN)[16]uses memory network[17](where richer information on the users’ knowledge states can be stored). Some researchers[18-19]used the attention mechanism[20]to prevent the models from discarding important information in the future. Specifically, self-attentive knowledge tracing (SAKT)[21]uses transformer[22]to enable faster training process and better prediction performance. These deep learning-based models are superior to the traditional models in that they have no extra requirements on the partition of skills. However, they are used to either assess the mastery of skills, or predict the probability that a problem can be solved. Even though some models[18]can assess and predict at the same time, the assessments are not convincing enough because of not being used in the predictions and only being evaluated according to the experts’ experience. Other researchers[23-24]integrated the traditional methods into the deep learning models, making assessing and predicting at the same time possible. Yet, their proposed models still had constraints for the partition of skills.
In this paper, a novel knowledge tracing model, which makes use of both DKT and knowledge graph embedding (KGE)[25-29], is proposed. DKT has the capacity of assessing users and has no extra requirements on the partition of skills. KGE can be used to make inferences on whether two given entities (such as users and problems) have certain relation (such as a user is capable of solving a problem). A combination of both has the power to assess and predict simultaneously. Three datasets are used to evaluate the proposed model, compared with the state-of-the-art knowledge tracing models.
1 Problem Formalization
Individualized learning involves user assessment and personalized prediction. In an online learning platform, suppose there areKskills,Qproblems, andNusers. A user’s submissions (or attempts)s={(e1,a1), (e2,a2), …, (et,at), …, (eT,aT)} is a sequence, whereTis the length of the sequence,etis the problem identifier andatis the result of the user’stth attempt (1≤t≤T). If the user correctly solves problemet,at= 1, otherwiseat=0.
Definition1User assessment: given a user’s submissionss, after theTth attempt, assess the user’s mastery of all the skillsyT= (yT, 1,yT, 2, ...,yT, j, ...,yT, K) ∈RK, whereyT, jis the mastery of thejth skill (0 ≤yT, j≤ 1, 1 ≤j≤K). yT, j=0 means the user knows nothing about thejth skill;yT,j= 1 means the user has already mastered thejth skill.
Definition2Personalized prediction: given a user’s submissionss, after theTth attempt, predict the probabilitypT+1(0 ≤pT+1≤ 1) that the user correctly solves problemeT+1in the (T+1)th attempt.
2 Deep Knowledge Tracing Embedding Neural Network (DKTENN)
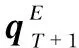
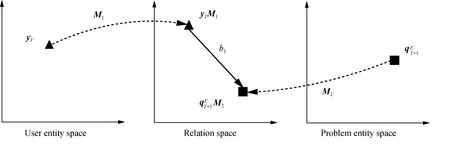
Fig. 1 Projection from the entity space to the relation space
2.1 Model architecture
As is shown in Fig. 2, DKTENN contains four components,i.e., user embedding, problem embedding, projection and normalization (proj. & norm.), and predictor.
Userembedding: a user’s submissionssis first encoded into {x1,x2, …,xt, …,xT}.xt= (qt,rt) ∈R2Kis a vector containing the required skills of problemetand the resultatin the user’stth attempt, whereqt,rt∈RK(1 ≤t≤T). If problemetrequires thejth skill (1≤j≤K),qt’sjth entry is one andrt’sjth entry isat, otherwise both of thejth entries are zero. DKT’s input is {x1,x2, …,xt, …,xT}, and its output is {y1,y2, …,yt, …,yT}, whereyt= (yt, 1,yt, 2, …,yt, j, …,yt, K)∈RK, andyt, jindicates the user’s mastery of thejth skill after thetth attempt (1≤j≤K, 1≤t≤T).
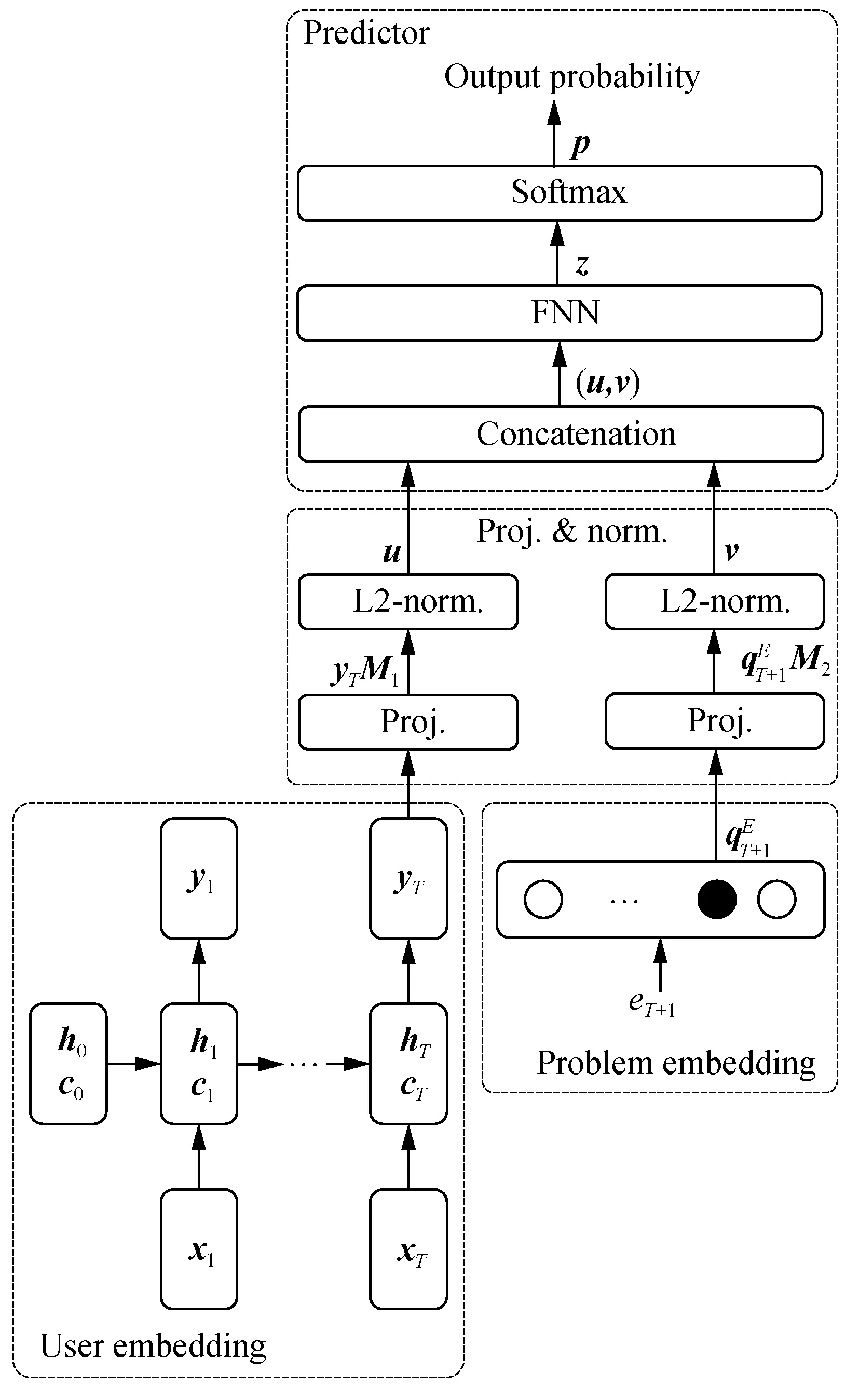
Fig. 2 Network architecture of DKTENN
In this paper, LSTM is used to implement DKT. The update equations for LSTM are:
it=σ(Wixxt+Wihht-1+bi),
(1)
ft=σ(Wfxxt+Wfhht-1+bf),
(2)
gt=tanh(Wgxxt+Wghht-1+bg),
(3)
ot=σ(Woxxt+Wohht-1+bo),
(4)
ct=ft*ct-1+it*gt,
(5)
ht=ot*tanhct,
(6)
whereWix,Wfx,Wgx,Wox∈Rl×2K;Wih,Wfh,Wgh,Woh∈Rl×l;bi,bf,bg,bo∈Rl;lis the size of the hidden states; * is the element-wise multiplication for matrices; andσ(·) is the sigmoid function:
(7)
ht∈Rlandct∈Rlare the hidden states and the cell states. Initially,h0=c0=0=(0, 0, …, 0) ∈Rl.
The assessments are obtained by applying a fully-connected layer to the hidden states:
yt=σ(Wy· dropout(ht) +by),
(8)
whereWy∈RK×l,by∈RK, and dropout(·) is used during model training to prevent overfitting[30].
DKTENN uses DKT’s outputyTas the user embedding, which is in the user entity space and summarizes the user’s capabilities in skill-level. In this paper, the DKT in user embedding differs from standard DKT (DKT-S) in the input and output. The input of DKT is a sequence of skill-level tags (xtis encoded usinget’s required skills) and the output is the mastery of each skill, while the input of DKT-S is a sequence of problem-level tags (xtis encoded directly usingetinstead of its required skills) and the output is the probabilities that a user can correctly solve each problem.
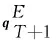
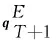
The projected vector ofyTisyTM1, whereM1∈RK× dis the projection matrix, anddis the dimension of the projected vector. The user vectoru∈Rdis the L2-normalized projected vector
(9)
whereεis added to avoid zero denominator, and ‖·‖2is the L2-norm. of a vector
(10)
wherey= (y1,y2, …,yd) ∈Rd, and |y| is the absolute value ofy.
Similarly, the problem vectorv∈Rdis:
(11)
whereM2∈RK×dis the projection matrix.
During predictions, the projection matricesM1andM2are invariant and independent of submissions.
Predictor: the prediction is made based on the user vectoruand the problem vectorv. The concatenated vector (u,v) ∈R2dis used as the input of a feed-forward neural network (FNN):
z=dropout(σ((u,v)W1+b1))W2+b2,
(12)
whereW1∈R2d×h,b1∈Rh,W2∈Rh×2,b2∈R2, andz= (z0,z1) ∈R2.
A final softmax layer is applied tozto get the final prediction
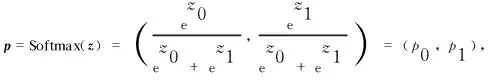
(13)
wherep0is the probability that the user cannot solve the problem, whilep1is the probability that the user can correctly solve the problem, andp0+p1= 1.
2.2 Model training
There are two parts in training. The first part is user embedding. In order to assess the users’ mastery of skills, following Piechetal.[8], the loss function is defined by
(14)
(15)
Considering DKT suffers from the reconstruction problem and the wavy transition problem, three regularization terms have been proposed by Yeung and Yeung[31]:
(16)
(17)
(18)
where ‖·‖1is the L1-norm. of a vector:
(19)
wherey= (y1,y2, …,yK) ∈RK.
The regularized loss function of DKT is:
(20)
whereλR,λ1andλ2are the regularization parameters.
The second part is problem embedding, proj. & norm. and predictor. The output of predictor indicates the probability. So, this part can be trained by minimizing the following binary cross entropy loss:
(21)
Adam[32]is used to minimize the loss functions. Gradient clipping is applied to deal with the exploding gradients[33].
3 Experiments
Experiments are conducted to show that: (1) DKT’s assessments are reasonable; (2) DKTENN outperforms the state-of-the-art knowledge tracing models; (3) KGE is necessary.
3.1 Datasets
The datasets used in this paper include users, problems and their required skills. The skills are partitioned according to the teaching experience of the domain experts. The data come from three publicly open online judges.
Codeforces(CF): CF regularly holds online contests. All the problems on CF come from these contests. The problems with their required skills labeled by the experts, 500 top-rated users and their submissions are prepared as the CF dataset.
HangzhouDianziUniversityonlinejudge(HDU) &PekingUniversityonlinejudge(POJ): the problems on HDU and POJ have no information on the required skills. Solutions from Chinese software developer network (CSDN) are collected and used to label the problems. The users who have solved the most problems and their submissions are prepared as the HDU and POJ datasets.
The details of the datasets are shown in Table 1, where the numbers of users, problems, skills and submissions are given. For each dataset, 20% of the users are randomly chosen as the test set, and the remaining users are left as the training set.
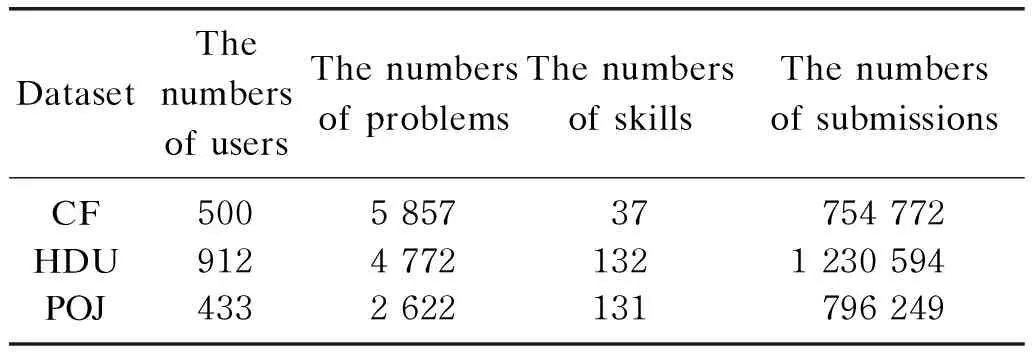
Table 1 Dataset overview
3.2 Evaluation methodology
Evaluationmetrics: the area under the ROC curve (AUC) and root mean square error (RMSE) are used to measure the performance of the models. AUC ranges from 0.5 to 1.0. RMSE is greater than or equal to 0. The model with a larger AUC and a smaller RMSE is better.
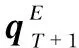
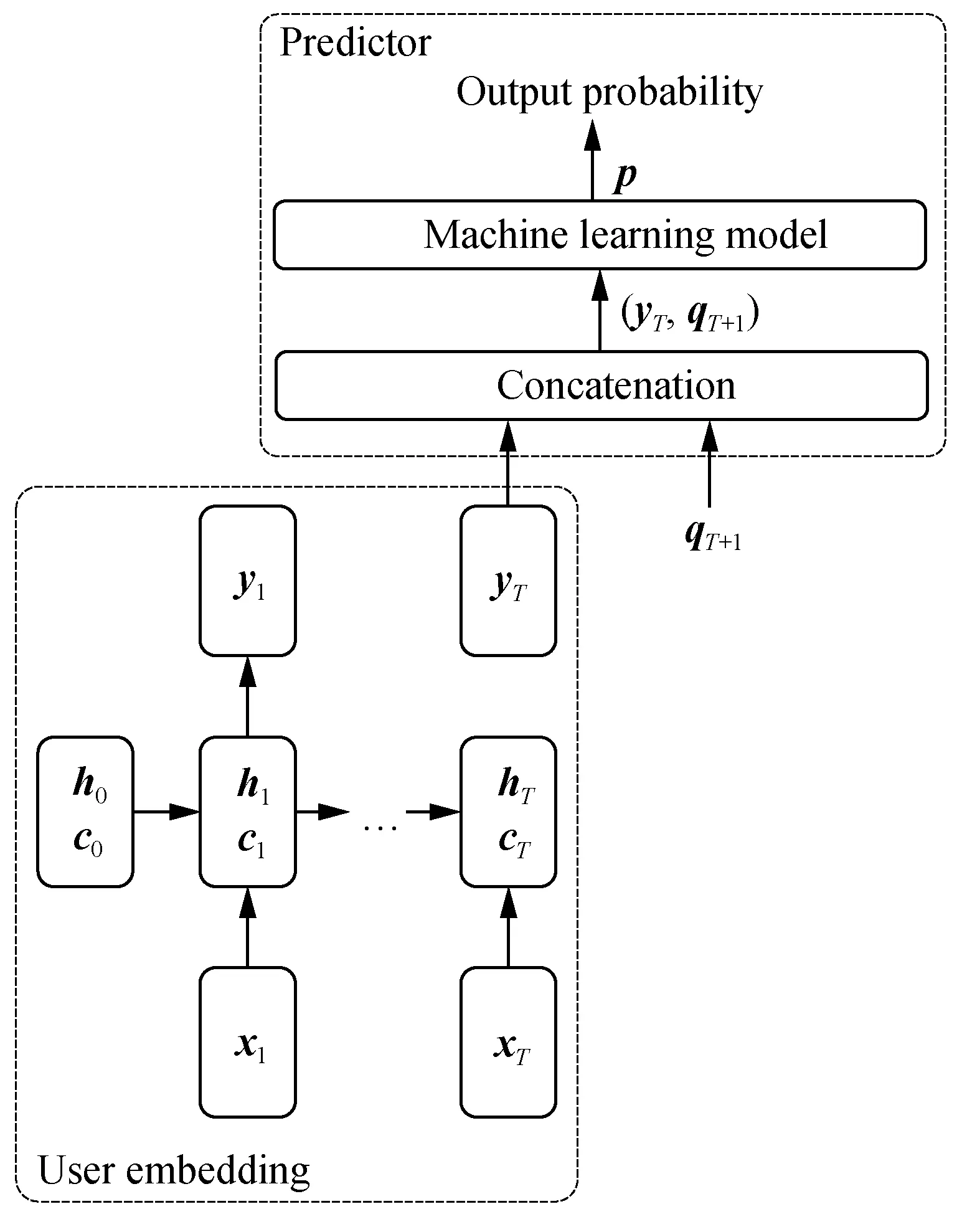
Fig. 3 Architecture of DKTML
3.3 Results and discussion
The results for user assessment are shown in Table 2. DKT outperforms BKT and BKT-F, and achieves an average of 35.6% and 17.3% gain in AUC, respectively. On the one hand, BKT can only model the acquisition of a single skill, while DKT takes all the skills into account and is capable of adjusting the users’ mastery of one skill based on another closely related skill according to the results of the attempts. On the other hand, as a probabilistic model relying on only four (or five) parameters, BKT (or BKT-F) has difficulty in modeling the relatively complicated learning process in programming contest. Benefited from LSTM, DKT has more parameters and stronger learning ability. Nevertheless, the input of DKT does not contain information such as the difficulties of the problems,i.e., if two users have solved problems requiring similar skills, their assessments are also similar, though the problem difficulties may vary greatly. Thus, DKT’s assessments are only rough estimations on how well a user has mastered a skill.
The results for personalized prediction are shown in Table 3. DKTENN outperforms the state-of-the-art knowledge tracing models over all of the three datasets, and achieves an average of 0.9% gain in AUC and an average of 0.6% decrease in RMSE, which proves the effectiveness of the proposed model.
To predict whether a user can solve a problem, not only the required skills, but also other information such as the difficulties, should be considered. Both DKTML and DKTENN are based on DKT’s assessments, but the difference is that DKTML uses the required skills in a straightforward manner, while DKTENN uses a method similar to KGE to make full use of the information such as the users’ mastery of skills and the problems’ difficulties besides the required skills. Compared to DKTFNN (having the best performance in all kinds of DKTML), DKTENN achieves an average of 2.5% gain in AUC, which shows KGE is an essential component.
Since the prediction of DKTENN is based on the assessments of DKT, better performance of DKTENN shows that the assessments of DKT are reasonable.

Table 2 Experimental results of user assessment
Figure 4 is drawn by projecting the trained problem embeddings into the 2-dimensional space using t-SNE[36]. The correspondence between the 50 problems and their required skills can be found in the Appendix. To some extent, Fig. 4 reveals that DKTENN is able to cluster similar problems. For example, problems 9 and 32 are clustered possibly because they share the skill “data structures”; problems 17 and 49 are both “interactive” problems. So, it is believed that the embeddings can help to discover the connections between problems. Due to the complexity of the problems in programming contest, further research on the similarity between problems is still needed.
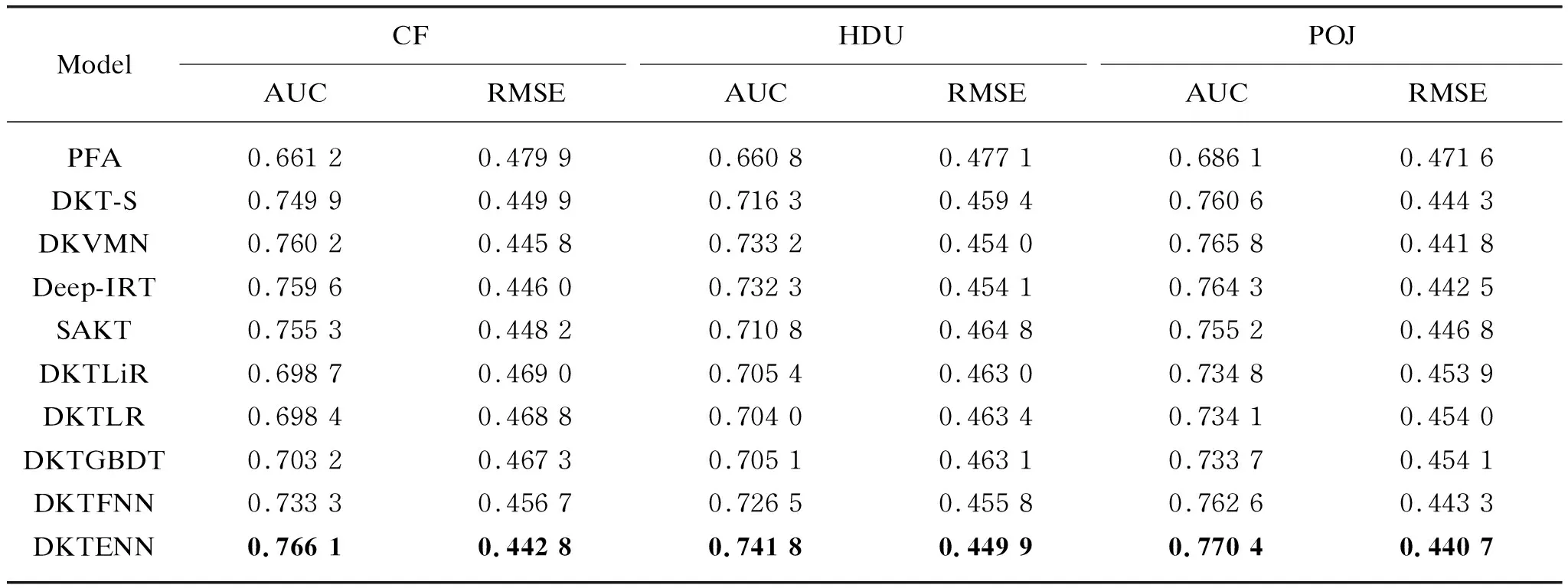
Table 3 Experimental results of personalized prediction

Fig. 4 Visualizing problem embeddings using t-SNE
4 Conclusions
A new knowledge tracing model, DKTENN, making predictions directly based on the assessments of DKT, has been proposed in this work. The problems, the users and their submissions from CF, HDU and POJ are used as datasets. Due to the perfect combination of DKT and KGE, DKTENN outperforms the existing models in the experiments.
At present, the problem or skill difficulties are not incorporated into the assessments of DKT. In the future, to further improve the assessments and the prediction performance of the model, better embedding methods will be explored to encode the features of problems and skills.
Table Ⅰ Selected CF problem and their required skills

(Table Ⅰ continued)
 Journal of Donghua University(English Edition)2020年6期
Journal of Donghua University(English Edition)2020年6期
- Journal of Donghua University(English Edition)的其它文章
- Prediction of Logistics Demand via Least Square Method and Multi-Layer Perceptron
- Effect of Different Types of Structural Configuration on Air Distribution in a Compact Purification Device
- Measurement of International Competitiveness of Clothing Industry under the Background of Value Chain Reconstruction
- Counterexample of Local Fractional Order Chain Rule and Modified Definition of Local Fractional Order
- Design and Application of Coordinator App Based on Needs Survey
- Optimization Method of Bearing Support Positions in a High-Speed Flexible Rotor System
