交互基函数在数据流聚类中的应用

朱颖雯

（三江学院计算机科学与工程学院，南京210012）

0 引言

数据流聚类已成为一个重要研究领域，其目标是在无序和潜在的无限序列中发现模式。故存储和随机访问所有数据点均不可行。至今许多数据流聚类算法被提出[1-17]，其均基于传统的聚类算法。可以将其分为5类：基于划分的方法（STREAM[1]）；基于层次的方法（CluStream[2]、HPStream[3]、SWClustering[4]、E-Stream[5]、REPSTREAM[6])；基于密度的方法（DenStream[7]、ACSC[8]、OPTICS-Stream[9]、incPre-Decon[10]）；基于网格的方法(D-Stream[11]、MR-Stream[12]、CellTree[13]）；基于模型的方法（SWEM[14]、GCPSOM[15]、G-Stream[16]、RPGStream[17]）。然而，这些算法均只考虑了特征与类别之间的相关性，并无考虑特征交互，但特征交互在各类学习任务中普遍存在。交互特征指的是那些特征与类别单独计算相关性时，表现为无关或极弱相关，但当与其他特征联合时，就可能与类别表现出极大的相关性[18]。

基于此本文将交互基函数（Interactive Basis Func⁃tions）用于数据流聚类以提高算法的聚类精度。首先，对到达的数据点根据特征之间的相关性通过预计算函数特征扩展，再进行聚类。交互基函数可生成灵活的决策边界且不需要指定软件，预计算函数可以在任何算法中实现，其可用于数据流聚类算法的任何扩展。

1 交互基函数

我们首先讨论基函数，用于训练的特征构成了基向量。例如，特征数p=2时，搜索空间即为特征正交轴构成的平面。每个特征是一个基向量。三个特征构成了一个3D基。如果把一个特征看作一个基向量，则基函数就是一个简单变换。最简单的情况，基函数可以是恒等式：

其为多项式函数特例，即当a=1时：

其他基函数也可以定义为指数形式：

基函数通常用于回归分析，在回归分析中基函数具有改变回归平面特性的作用。例如，从恒等到变量的平方的转换会使回归线变为抛物线。本文将其用于聚类分析，考虑K个候选实基函数bi：R→R，i=1,…,K。定义{b1,b2,…,bK}为一组基函数。利用此基函数增加T个新特征来放大p个特征集：

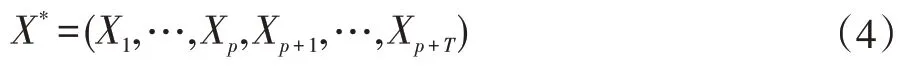
这里，X*∈Rp+T且Xp+i=bsi(Xji)，i=1,…,T，si∈{1,…,K}，ji∈{1,…,p}。考虑p=2，即X={X1,X2}。其中T=1，K=1，b1(x)=x2，则X*={X1,X2,X3=X12}。每当划分算法在X3中选择一个分割s时，其在X上的投影为，为一个常数。因此，基函数维数上的任何分割都等价于在原始的基上找到一个正交的决策边界。

由于基函数可在原始基中产生正交分区，我们的目标是在构造中使用交互基函数（IBFs）。这些相互作用可由一组D函数所识别，这些D函数体现了基函数的特征变换相互作用。定义交互函数为：

此设置下，定义：

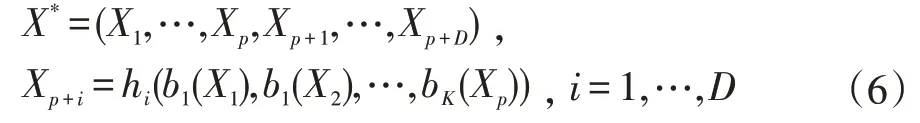
因此，通过对X*应用标准的递归划分方法，其在X上的投影将提供一个倾斜的划分（也可能是非线性划分），考虑到了特征之间的相互作用。例如p=2，即X={X1,X2}，T=1，K=1，b1(x)=x，D=1，h1(b1(X1),b1(X2))=b1(X1)+b1(X2)=X1+X2，且X*={X1,X2,X3}我们得到X3=s被投影到原基的平面上，即X2=s-X1，从而在该平面上给出倾斜划分。IBFs提供的框架除了倾斜分区外，还可引入非线性决策边界，这是通过在子空间X=(X1,…,Xp)中投影hi(b1(X1),b1(X2),…,bK(Xp))=a生成。例如，h1(b1(X1),b1(X2))=b1(X1)b1(X2)，由b1(x)=x得到X1X2。固定了X1X2=s，因此X2=s/X1，从而创建了一个双曲分割。

最后一个例子，h1(b1(X1),b1(X2))=b1(X1)+b1(X2)，b1(x)=x2导 致X12+X22。固定X12+X22=s，得到，从而形成一个径向划区。

2 数据流聚类

设数据流DS为一个带有时间戳（Time Stamp）的多维数据点集合，DS={x1,x2,…,xn}（实际应用中n的取值可以为无限大），其中每个数据点xi=(xi1,xi2,…,xid)是一个d维的数据记录，其到达时间为ti。数据流聚类将数据DS中的相似对象划分为一个或多个组（称为“簇”，Cluster），划分后，同一簇中的元素彼此相似，但相异于其他簇中的元素。基于交互基函数相关理论，可以在使用数据流聚类算法之前，首先对d维特征进行扩充，扩充到d+T特征再进行聚类。此方法不仅对离线数据流聚类适用对在线数据流聚类也同样适用。具体算法如下：

算法1.IBFs_DS算法.

输入：DS={x1,x2,x3,…}；

输出：节点集合C={c1,c2,c3,… 及其权值W={wc1,wc2,wc3,…,}．

①for eachxi

②使用式（6）构造xi*;

③对xi*使用各种数据流聚类算法进行聚类；

④end for

3 结语

本文将交互基函数（IBFs）用于数据流聚类以提高算法的聚类精度。首先，对到达的数据点根据特征之间的相关性通过预计算函数特征扩展，再进行聚类。交互基函数可生成灵活的决策边界且不需要指定软件，预计算函数可以在任何算法中实现，其可用于数据流聚类算法的任何扩展。